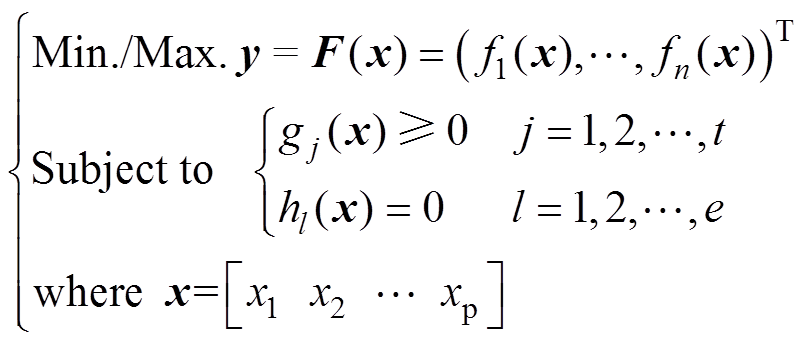（1）摘要 IGBT的选择对功率变换器的效率、可靠性和成本均有重要影响，是变换器设计阶段要解决的首要问题。然而，目前在功率变换器的设计中，IGBT及开关频率的选择更多依赖于设计者的经验，缺乏明确的理论依据。为此，该文提出一种新颖的基于多目标优化的电动汽车（EV）变流器设计方法。首先，建立了基于行驶工况的，与变流器损耗、可靠性和成本相关的三个性能评价指标；然后，通过所设计的多目标优化流程，获得了以IGBT和开关频率为设计变量的Pareto最优解集；最后，采用层次分析法选取一个最优解并进行实验验证。
关键词：电动汽车变流器 多目标优化 可靠性 成本
由于环境保护和全球能源危机，近年来电动汽车（Electric Vehicle, EV）已经吸引了越来越多国家的关注，发展非常迅速[1-4]。作为驱动系统中的关键单元，变流器对电动汽车的性能有重要影响，而功率器件是变流器中最脆弱的元件之一，且占其绝大部分损耗。有关可靠性调研报告表明，在电力电子系统中，由功率器件和电容器引起的设备故障率最高，约占50%[5-6]。因此，选择合适的功率器件（如IGBT）是变流器设计阶段最重要的任务之一。
通常，IGBT的选择主要取决于变换器电压等级和通流大小。此外，为了确保IGBT的长期安全运行，其结温不能超过允许最大值。然而，IGBT结温的计算是一个相对复杂的过程，它不仅取决于器件功率损耗和热特性，还与冷却系统和环境温度等因素有关。为了简化IGBT的选择过程，功率模块制造商通常提供损耗计算软件，如Infineon IPOSIM和Semikron DriverSel，这些软件可以在相对简单的热模型的基础上，近似计算出功率器件的平均损耗和结温变化情况。近年来，工业界和学术界逐渐在功率器件的选择方面进行了更多的探索。文献[7]通过考虑栅极电阻、直流母线电压和环境温度，提出了一种用于逆变器的IGBT选择方法。此外，文献[8-9]指出，在航空航天领域，不仅要考虑电压、电流和安全工作区域，还要考虑器件的尺寸和重量来选择元器件。除此之外，开关频率也是变流器的一个重要设计因素，因为它对IGBT的功率损耗、无源器件的体积、电磁干扰等都有很大的影响。文献[10]从电磁兼容（Electromagnetic Compatibility, EMC）方面研究了开关频率的选择，文献[11]从降低电机电磁噪声的角度阐述了电力电子变换器开关频率的选择方法，而文献[12]从功率密度和功率损耗两方面分析了开关频率对变换器性能指标的影响。
综上所述，IGBT和开关频率的选择已经从早期的依赖工程经验转变到考虑变换器的性能优化上。美国能源部制定的电动汽车发展路线图指出，到2025年，电动汽车的安全行驶里程必须达到15年或超过48万km[13]。因此，除了效率和功率密度外，EV变流器还需要满足可靠性和寿命的要求。此外，在汽车工程中，设计师总是希望将成本降到最低，以保持其市场竞争力[2]。然而，对电力电子系统而言，以上性能指标往往是相互冲突的，即不可能在保证最低成本的同时，获得最高的效率和寿命。
多目标优化是解决这个问题的方法之一[14]。为此，本文提出了一种新的EV变换器优化设计方法来选择最合适的功率器件和开关频率，主要贡献包括：①基于综合多目标优化选择IGBT和开关频率，以实现变流器能量损耗、寿命和成本之间的最佳折中；②建立了基于汽车都市循环工况下的EV变流器性能评价函数。众所周知，传统的功率密度和效率等性能指标通常是在额定工况下获得的。然而，在实际行驶工况期间，变流器消耗的能量是时变的。因此，只有基于汽车都市循环工况建立的性能评价函数才能反映EV实际运行状况。
为了改善IGBT及其开关频率的选择方法并设计一个高性能的EV变流器，本节采用了基于Pareto优化的设计方法。
一般来说，多目标优化问题往往由两个或两个以上的目标函数和约束条件组成，其可以描述[15]为
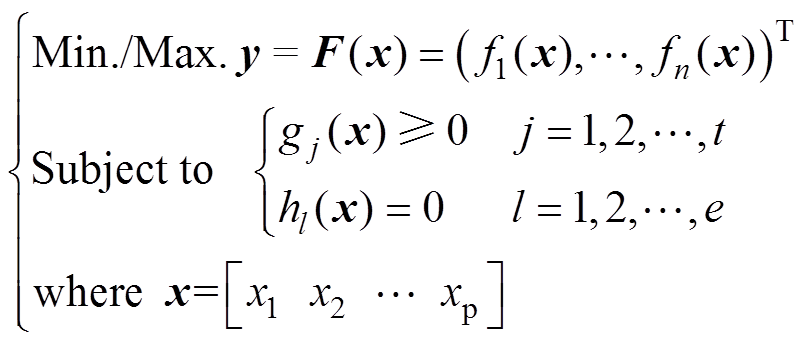（1）式中，x为p维决策向量；y为n维目标向量；g(x)和h(x)分别为多目标优化的不等式和等式约束。
在多目标优化问题中，当目标函数间处于冲突状态时，不存在使所有目标函数同时达到最大值或最小值的全局最优解，只能找到非劣解（或Pareto最优解）。所谓非劣解是指由这样一些解组成的集合（又称非劣解集），与集合之外的任何解相比，它们至少有一个目标函数比集合之外的解好，而其他目标函数又不比集合之外的解差[16]。两目标函数优化问题的Pareto前沿[15]如图1所示。从图1中可以看出，两个目标都要求越小越好，但目标之间是相互冲突的，即改善其中一个目标函数值就意味着牺牲另一个目标函数值，其在Pareto前沿上可以找到两个目标的最佳折中。
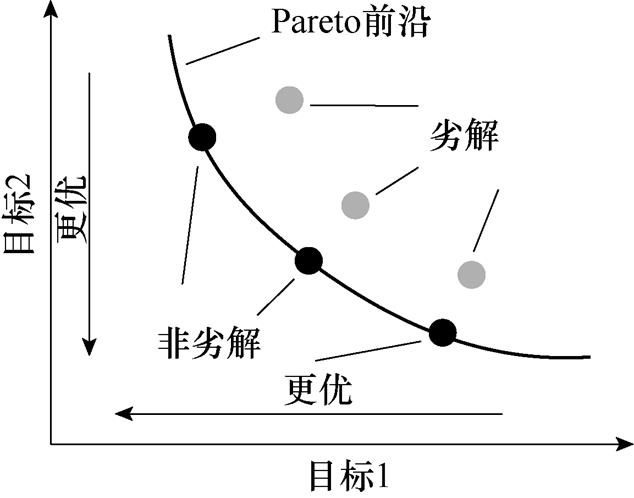
图1 两目标函数优化问题的Pareto前沿
Fig.1 Pareto front of a bi-objective optimization problem
变流器对电动汽车的性能有着重要影响，其性能的优劣可以通过相应的性能评价指标来衡量。本文从效率、寿命和成本的角度确定EV变流器的IGBT及其开关频率。由于电动汽车实际工作状态转换迅速，变流器的功率损耗实时变化，使得固定工况下定义的功率密度和效率等性能指标不能准确地反映EV变流器的运行指标。为此，对于图2中所示的典型电压源型（Voltage Source Inverter, VSI）EV变流器，本文将采用三个新的评价指标评估变流器的性能优劣。
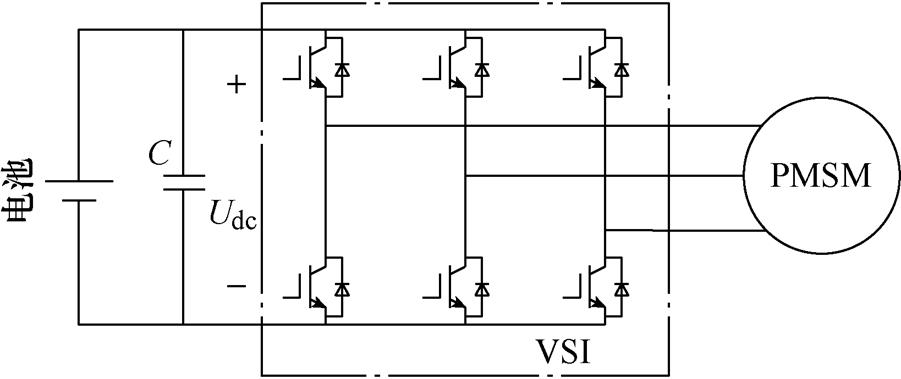
图2 EV变流器原理
Fig.2 The Schematic of EV converter
（1）能量损耗率（Energy Losses Per Kilometre, ELPK）。ELPK表示的是实际行驶工况内EV变流器消耗的能量，可表示为
（2）式中，Ei为EV实际行驶工况内变流器第i个元件的能量损耗；L为汽车的行驶距离。当采用城市道路循环（Urban Dynamometer Driving Schedule, UDDS）工况时，L=11.99km。
（2）首次平均故障里程（Mean Distance of First Failure, MDFF）。MDFF是指在变流器在第一次故障之前车辆行驶的总里程，可表示为
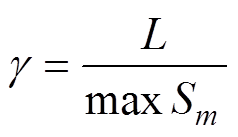（3）式中，Sm为变流器中由温度引起的第m个元件的累计损伤。
需要说明的是，在本文中，上述两个目标函数仅涉及IGBT，这是因为IGBT比薄膜电容器消耗更多能量，也更脆弱，详细的原因将在第3部分介绍。
（3）单位成本（Cost Per Watt, CPW）。CPW是指变流器总成本与额定输出功率之比。一般元器件的成本包含两部分：直接成本和间接成本。EV变流器的直接成本包括电源模块、散热器和电容器的采购成本；间接成本包括设备维护、员工工资等费用[17]。为简单起见，本文仅考虑元器件的直接成本。假设变流器的额定输出功率为Pout，则CPW可定义为
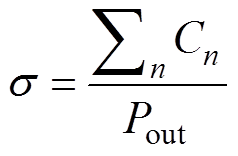（4）式中，Cn为变流器中第n个元件的成本。
众所周知，由于IGBT额定电流与芯片总面积成正比，且IGBT的损耗和无源元件的体积都受开关频率的影响，本文将IGBT的芯片面积Achip和开关频率fsw作为设计变量。根据上述分析，EV变流器的目标函数可以统一写成
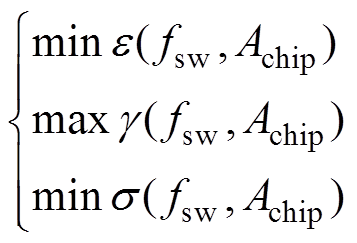（5）此外，为了保障设备安全可靠运行，需要根据设计技术规范、物理限制和元件的安全工作区域来定义一些约束条件。在本文中，EV变流器的设计约束包括IGBT的最大结温Tjmax和直流母线的电压纹波Du限制，可表示为
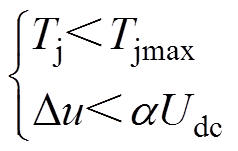（6）
式中，Tj为IGBT结温；a 为电压纹波率；Udc为额定母线电压。
从数学角度来看，电力电子变换器设计中的目标函数通常是多目标和非凸的。近年来，电力电子系统的多目标优化设计受到越来越多的关注，如文献[18]采用遗传算法（Genetic Algorithm, GA）来优化升压转换器的效率和成本。进一步地，针对电力电子变换器，文献[19-21]采用直接搜索方法（Direct Search Method, DSM）列举了所有可能的设计方案来搜索Pareto最优解。与其他算法相比，DSM可以通过搜索Pareto前沿全面列举所有可能的设计变量，以确保解的全局最优。本文采用了这种方法，设计的具体流程如图3所示。
首先，根据汽车和驱动电机模型，把汽车行驶工况转换成电压、电流和功率因数等电气参数。然后，利用稍后将介绍的电热模型计算不同设计变量（Achip和fsw）下IGBT的功率损耗和结温曲线。如果结温大于Tjmax，则更改设计变量并重新计算，直到结温满足约束条件为止。进一步，根据元件寿命模型计算IGBT的累积损伤，计算变流器的ELPK和MDFF。与此同时，散热器体积可以通过计算得到的变流器损耗确定，并根据母线电压纹波约束Du确定DC-link电容大小。最后，计算包括IGBT、电容器和散热器在内的整个变流器的成本，进而计算前面定义的三个评价函数值。至此，可以获得一组满足约束条件的可行解。修改设计变量并重复上述步骤，直到找到所有可行解，形成可行解集。在此基础上，根据Pareto支配关系确定EV变流器的Pareto前沿。最后，采用分层优化的方法对所有目标函数按其重要性分层排序，确定最佳设计方案。
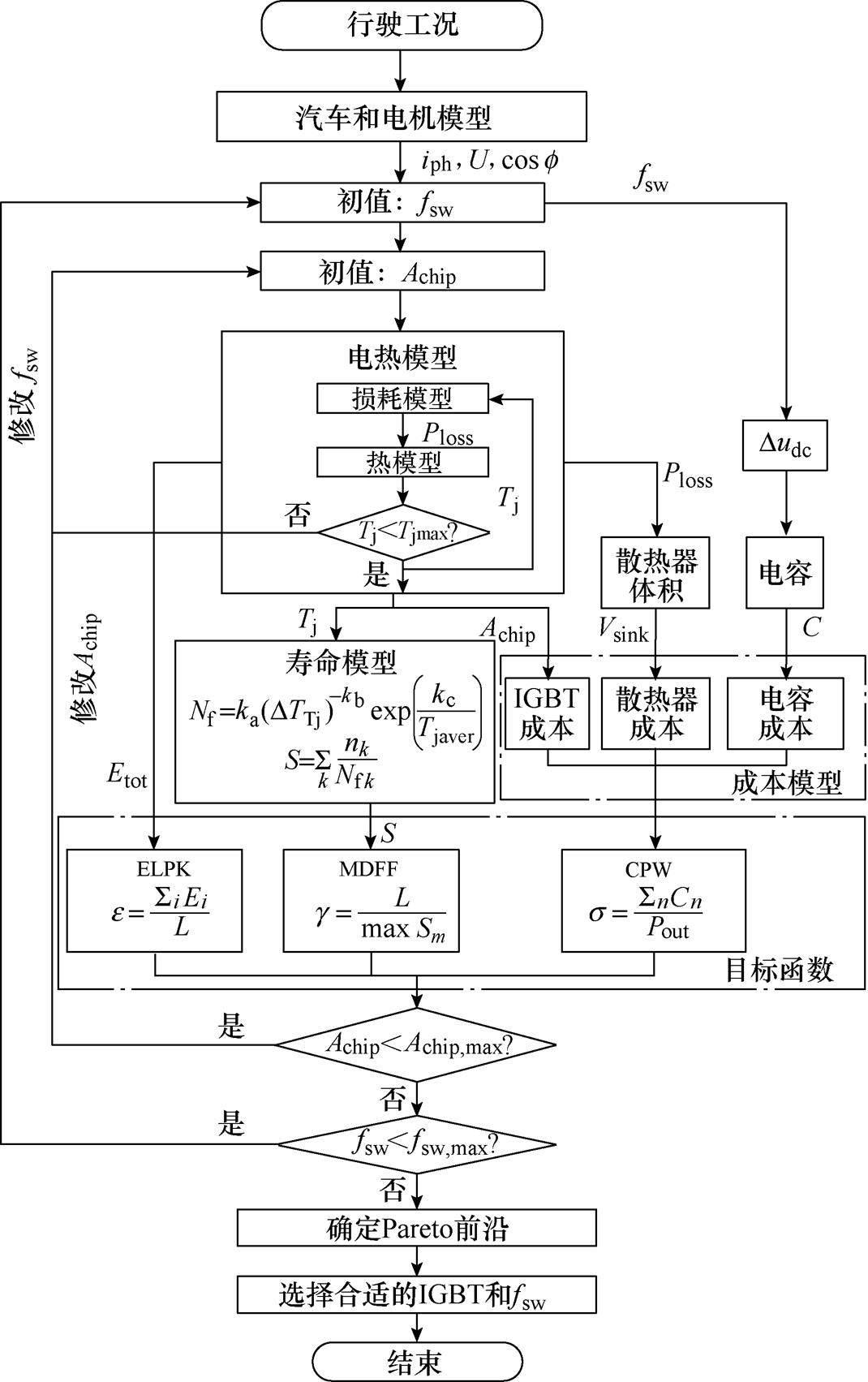
图3 多目标优化设计流程
Fig.3 The flowchart of the multi-objective optimization design
在研究电动汽车的动力性能时，一般采用平坦路面上行驶的纵向动力模型[22]，有
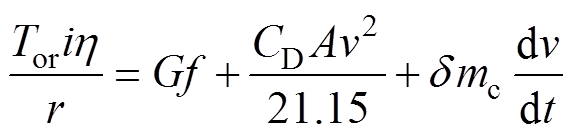（7）式中，Tor为电机的输出转矩；i为传动比；h 为传动系统总效率；r为驱动轮的滚动半径；G为电动汽车的重量；f为滚动阻力系数；CD为空气阻力系数；A为电动汽车迎风面积；v为相对速度（在无风时的汽车行驶速度）；d为旋转质量换算系数；mc为电动汽车质量。根据式（7），采用Matlab/Simulink软件就能搭建起电动汽车的仿真模型。本文以一小型EV为例，其详细参数见表1。
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）具有结构简单、体积小、质量轻、损耗低、效率高、功率因数高等优点，常被选为EV的驱动电机。本文采用转子磁链定向的矢量控制方法（Field Oriented Control, FOC），详细的电机参数见表2。由（7）式可获得UDDS工况下电机的速度和输出转矩曲线，如图4所示。从图4中可以看出，EV在起动或减速阶段，输出转矩变化剧烈；而在匀速行驶阶段，输出转矩变化小。
表1 电动汽车参数
Tab.1 Parameters of EV
参 数数 值 汽车质量mc/kg1 150 迎风面积A/m22.34 空气阻力系数CD0.4 滚动阻力系数f0.015 旋转质量换算系数d1.08 轮胎半径r/m0.297 传动效率h0.95
表2 电机参数
Tab.2 Motorparameters
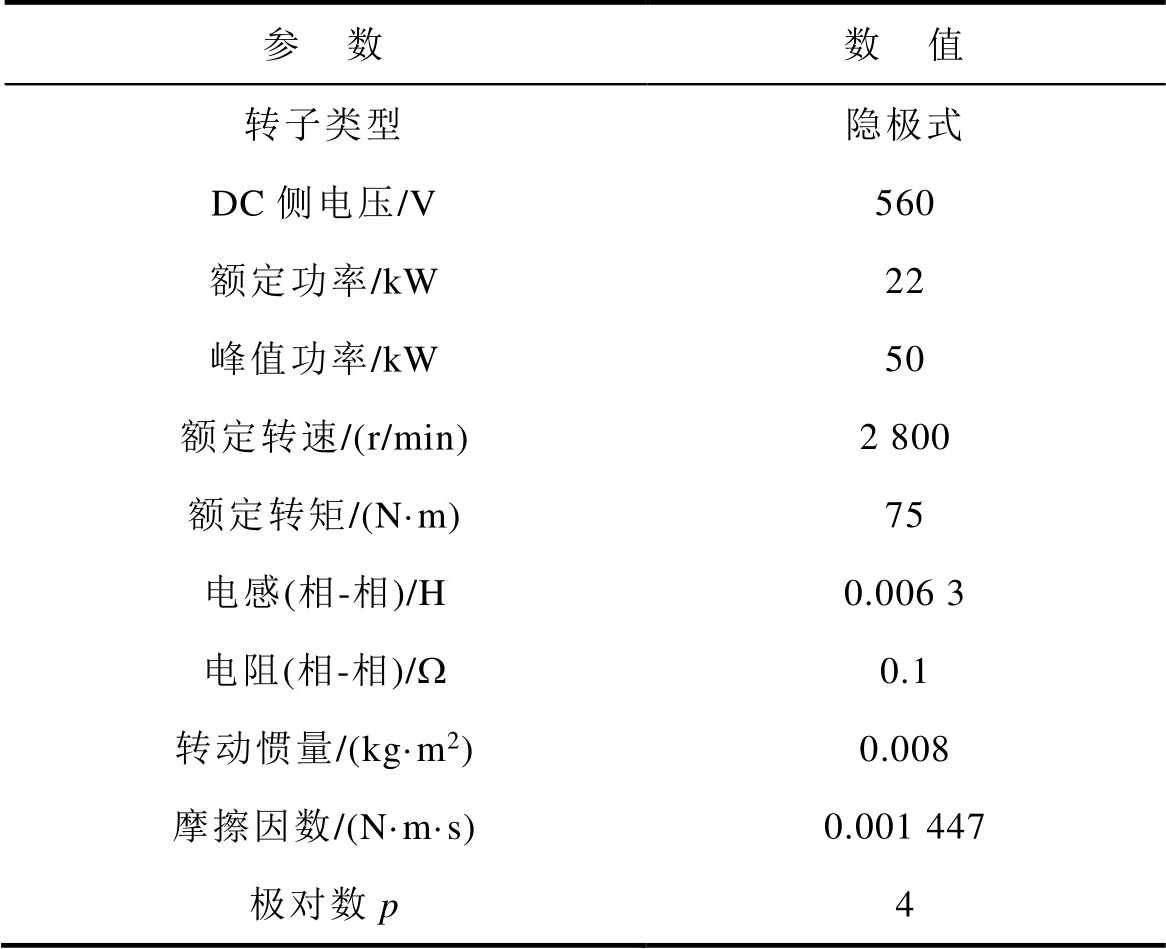
参 数数 值 转子类型隐极式 DC侧电压/V560 额定功率/kW22 峰值功率/kW50 额定转速/(r/min)2 800 额定转矩/(N·m)75 电感(相-相)/H0.006 3 电阻(相-相)/W0.1 转动惯量/(kg·m2)0.008 摩擦因数/(N·m·s)0.001 447 极对数p4
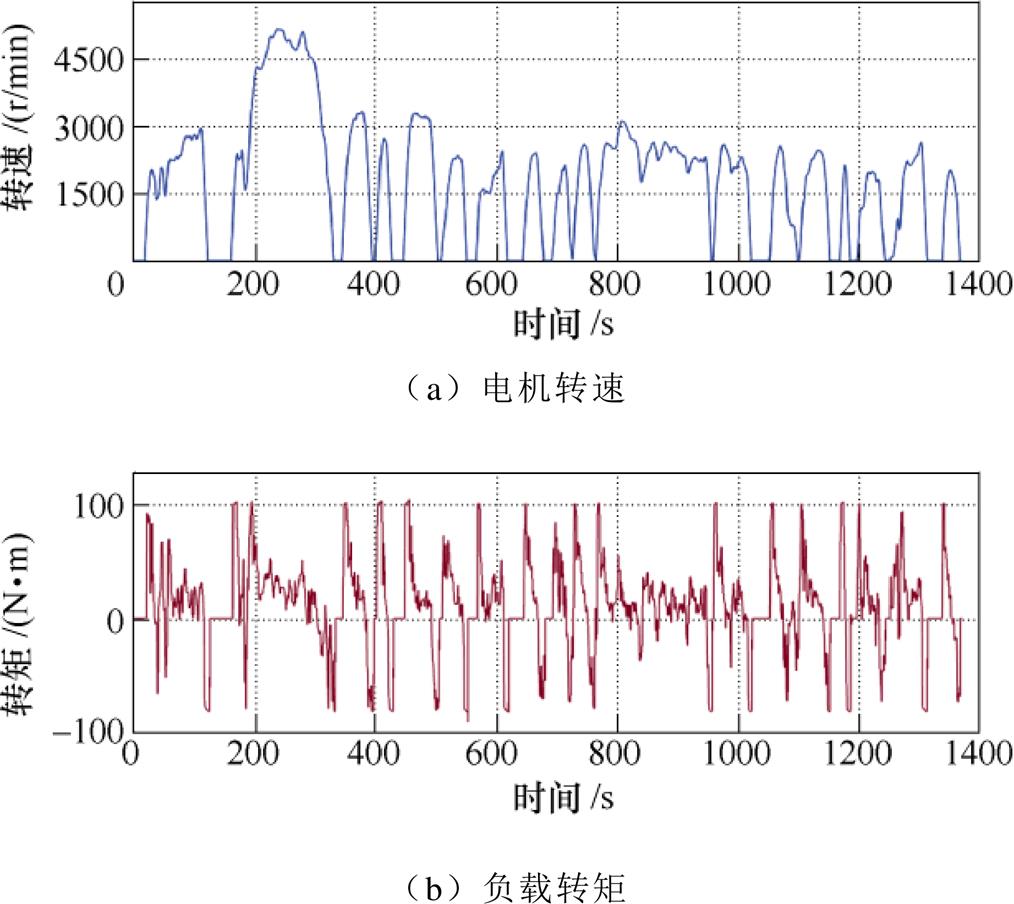
图4 UDDS工况下电机转速及负载转矩
Fig.4 Motor speed and load torque in UDDS
本节将详细介绍图3优化过程中使用的元件模型，包括IGBT、电容器和散热器。
功率器件的损耗和寿命与其结温及结温波动幅值密切相关，结温越高或波动幅值越大，其功率循环寿命就越短[23-25]。为了获得IGBT的结温和寿命曲线，首先需要建立如图5所示的EV变流器电热仿真模型，其主要包括行驶工况、汽车模型、电机模型、逆变器模型、损耗模型、电热模型和寿命模型。
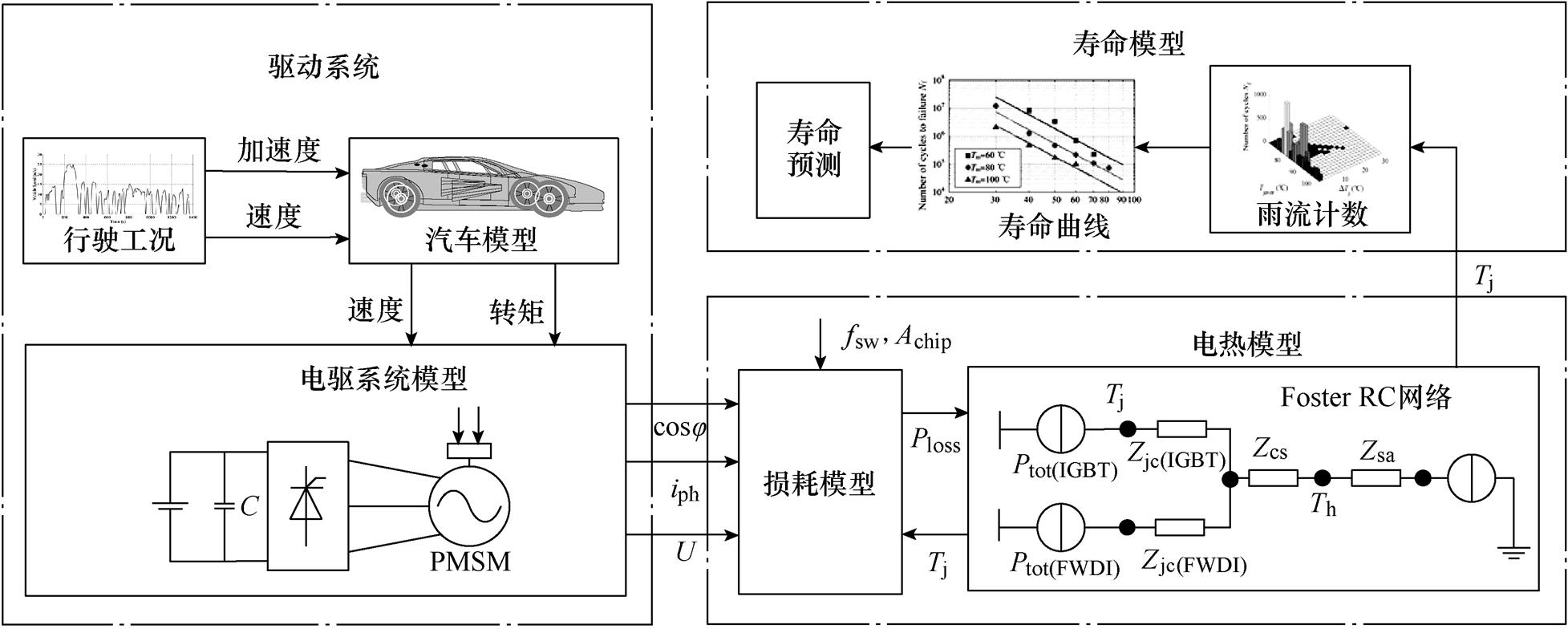
图5 EV变流器电热仿真模型
Fig.5 The electro-thermal simulation block diagram of EV converter
从工程角度讲，影响半导体价格和性能的两个关键因素是芯片面积和封装技术。其中，芯片面积决定IGBT通流能力；对于封装技术，各个公司采用的技术存在一定差异，相同规格、不同公司产品的某些参数也会不同（如热阻和寄生电感），且价格差别较大。考虑以上因素，针对同一公司的系列产品（相同封装技术）进行比较分析。本文以下分析都是基于Infineon公司的额定电压为1 200V的FSxxR12KT4系列IGBT模块，其详细参数见表3。此外，由于IGBT产品的芯片面积是不连续的，可能没有实际产品恰好与最终优化结果对应，可以选择最接近的产品。
表3 IGBT模块参数
Tab.3 Parameters of IGBT Modules
IGBTs芯片型号IGBT芯片面积/mm2 FS50R12KT4IGC50T120T8RL49.59 FS75R12KT4IGC70T120T8RL70.32 FS100R12KT4IGC99T120T8RL98.71 FS150R12KT4IGC142T120T8RL142.05
3.1.1 IGBT的损耗模型
文献[23]提出了采用芯片单位面积电流的方法来研究光伏逆变器的年度能量损耗，从而获得最佳芯片面积。本节拟采用该方法，研究UDDS工况下，IGBT损耗和结温变化特性，为下一步寿命分析做准备。
功率器件的损耗包括IGBT和反并联二极管（Freewheeling Diode, FWDI）的开关和导通损耗，它们都与开关频率fsw和芯片结温Tj都有关，其中IGBT的导通和开关损耗[23]可分别表示为
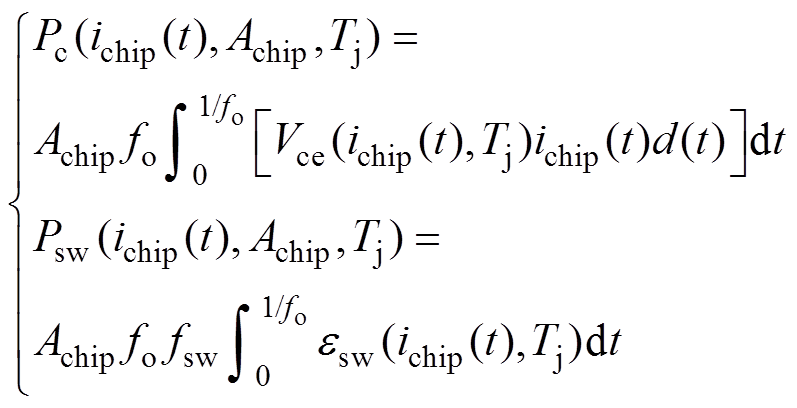（8）式中，fo为输出电流频率；ichip(t)=iph(t)/Achip为芯片电流密度，其中，iph(t)为输出相电流；d(t)为占空比；Vce(ichip(t),Tj)和εsw(ichip(t), Tj)分别为单位面积的通态压降和开关能量损耗函数，它们都与IGBT结温和芯片电流密度有关，其中结温Tj的计算方法将在后续部分详细介绍。
类似地，采用同样的方法可以计算FWDI的导通和开关损耗。需要说明的是，式（8）中，Achip指的是IGBT的芯片面积，而实际上同一模块中的IGBT和FWDI的面积不同。为了简化分析，本文将FWDI的芯片面积折算至IGBT。根据式（8），可以得到不同设计变量和参数条件下的单个开关（IGBT+FWDI）总损耗曲线，如图6所示，其中，实线表示结温超过150℃。从图6中可以看出，半导体总损耗将随着芯片面积的增加而减小，但是当相电流较小时，总损耗的减小幅度非常小。例如，与电流为60A时的工况相比，30A时的半导体功率损耗随芯片面积的变化要小得多。
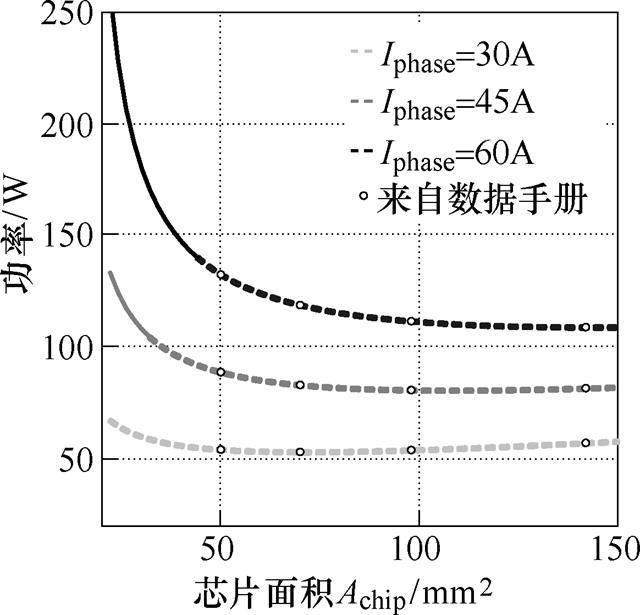
图6 不同工况下，单个开关的总损耗与芯片面积的关系（Tamb=70℃, fsw=10kHz, cosj =1）
Fig.6 Power losses of one switch vs. chip area (Tamb=70℃, fsw=10kHz, cosj =1)
3.1.2 IGBT的寿命模型
瑞士的LESIT项目组测试了不同厂家的标准工艺封装的IGBT模块，总结出了IGBT模型寿命模型[26-27]为
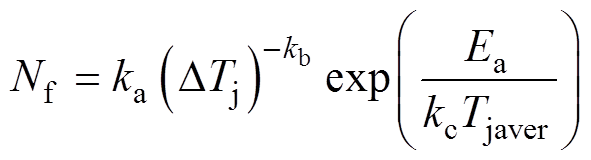（9）式中，Nf为故障循环次数；ka和kb为拟合系数；DTj为结温变化幅度；Ea为激活能；Tjaver为结温平均值；kc为玻尔兹曼常数。
IGBT的结温Tj(t)可表示为
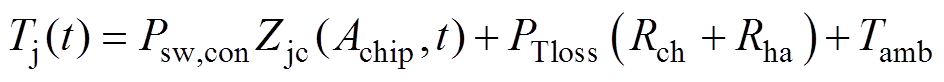（10）式中，Psw,con为单个IGBT的功率损耗；Zjc(Achip,t)为热阻抗；PTloss为模块的总损耗；Rch为壳-散热器间的热阻；Rha为散热器-环境间的热阻；Tamb为环境温度，这里指的是冷却水的入口温度。同理，二极管结温的计算方法与IGBT相同，这里不再赘述。
根据上述分析，在Matlab中建立如图5所示的电热仿真模型，可得到UDDS循环工况下EV变流器中单个IGBT芯片的功率损耗Ploss和结温Tj变化曲线，如图7所示。从图中可以看出，结温Tj在电动汽车启动阶段或加速阶段波动幅值剧烈，而在车辆稳定运行或减速制动时，波动较小。
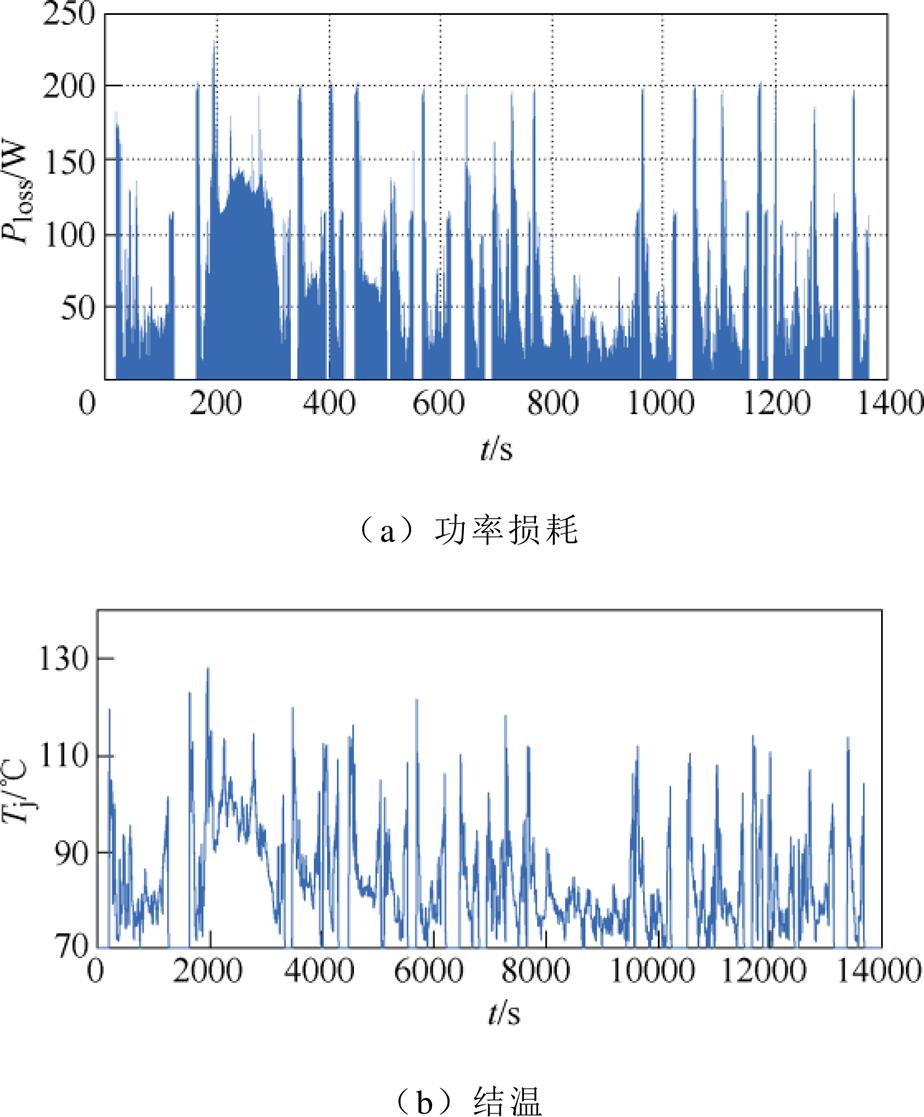
图7 UDDS循环工况下单个IGBT芯片的损耗和结温曲线（fsw=10kHz, Achip=70mm2）
Fig.7 IGBT power losses and junction temperatures under UDDS cycle ( fsw=10kHz, Achip=70mm2)
进一步地，为了预测IGBT模块的寿命，采用雨流计数法提取出不同Tjaver和DTj时的温度循环周期数。然后，根据疲劳损伤的线性累积理论计算出器件总损伤[28]为
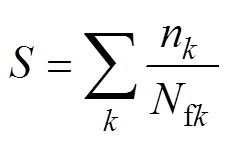（11）式中，nk为相应的Tjaver和ΔTj的温度循环周期次数；Nfk为相应的故障温度循环次数；SÎ(0, 1)，当S=1时，器件损坏。
3.1.3 IGBT的成本
成本是企业成功和可持续竞争优势的关键。在本文中，IGBT的成本是从经销商或制造商处获得的基于最小订货量（Minimum Order Quantity, MOQ）为2 500个的价格。同样的方法也用于获得其他元件（电容器和散热器）的成本数据。
对于同一系列的IGBT模块，其成本与芯片面积成线性关系，如图8所示。因此，IGBT模块的成本模型可表示为
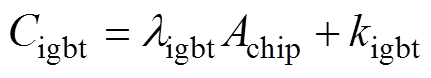（12） 式中，ligbt为单位面积成本；kigbt为封装成本（包括芯片集成和焊接）。不同类型的IGBT模块，其成本拟合系数见表4。
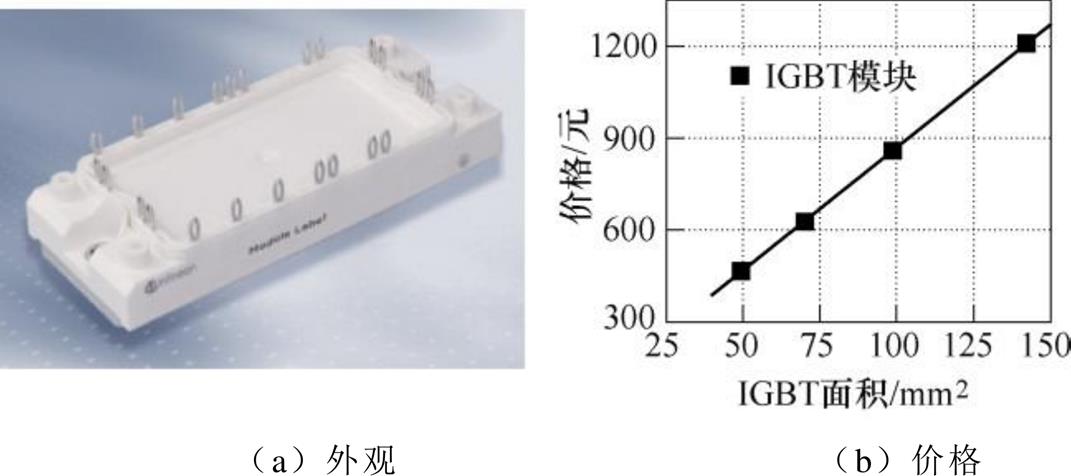
图8 IGBT模块的外观和价格
Fig.8 IGBT module appearance and unit price
表4 各元件的成本拟合系数
Tab.4 Cost fitting coefficients of different components
IGBT模块铝制水冷散热器薄膜电容 lx7.655/(元/mm2)117.38/(元/dm3)4.72/(元/mF) lx/元65.64117.324.05
功率器件产生的热量会导致器件温度升高，危及设备的正常工作。因此，需要设计合适的散热系统，把这部分热量带走。在本文的优化设计中，采用水冷散热系统。出于简化目的，本文按在峰值输出功率下保持散热器与环境间的温差为15℃来设计散热器和冷却系统。因此，散热器-环境间的热阻可表示为
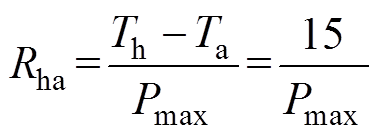（13）式中，Th为散热器与IGBT模块的接触表面温度；Ta为散热器进水温度；Pmax为IGBT的峰值损耗功率。
水冷散热器的种类众多、价格悬殊，可优化的变量众多（材质、沟槽数、沟槽尺寸、翅片、温度等），很难将众多变量融入到系统的多目标优化设计中。苏黎世联邦理工学院的Kolar教授提出了一种确定冷却系统性能指标（Cooling System Performance Index, CSPI）方法[29]为
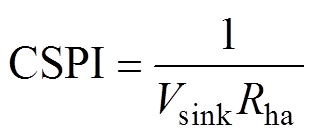（14） 式中，Vsink为散热器体积。这样，选定一种散热器，通过散热器体积这个变量，可以将散热器的热模型纳入系统的优化设计中。对候选的国内某厂家生产的双水道铝挤型散热器，按照文献[30]的方法进行了热阻计算，分析了固定水温（70℃），散热器体积变化时（实际中仅长度变，宽和高不变，宽和高为100mm×20mm）的CSPI，如图9所示。可以看出，当体积变化时，通过微调冷却水流速可以保持 CSPI基本稳定。为此在本文中假定CSPI保持在210W/(dm3·K)不变，这样就可以通过式（14）计算得到合适的水冷板尺寸。
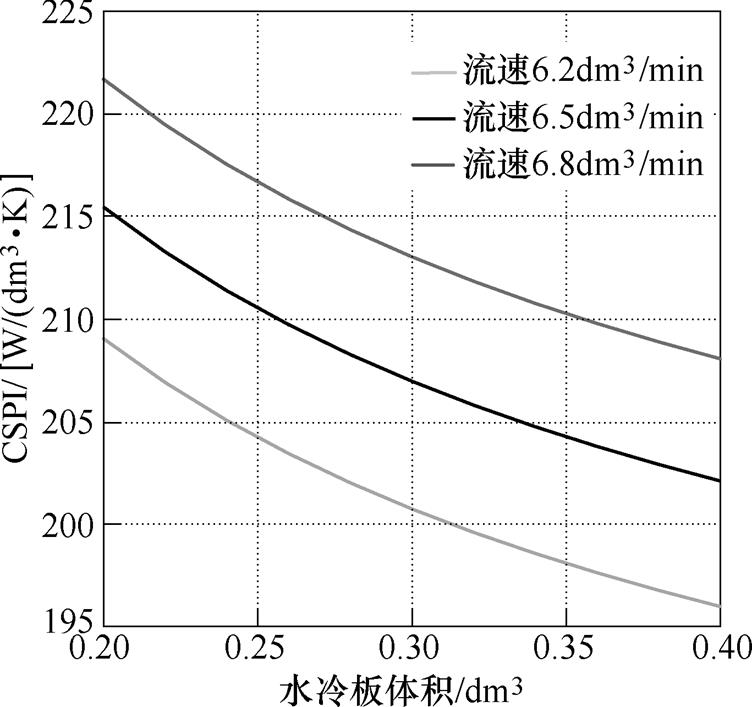
图9 不同体积散热器的CSPI
Fig.9 CSPI of heatsink with different volume
水冷板的成本通常取决于材料的体积或重量以及制造和加工成本，图10b所示的是国内某铝制水冷板的价格曲线。从图中可以看出，水冷板的价格与体积成线性关系，则其成本可表示为
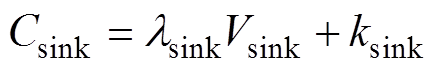（15） 式中，lsink为与散热器类型有关的单位体积成本；ksink为固定成本（打孔、切割等），拟合系数见表4。
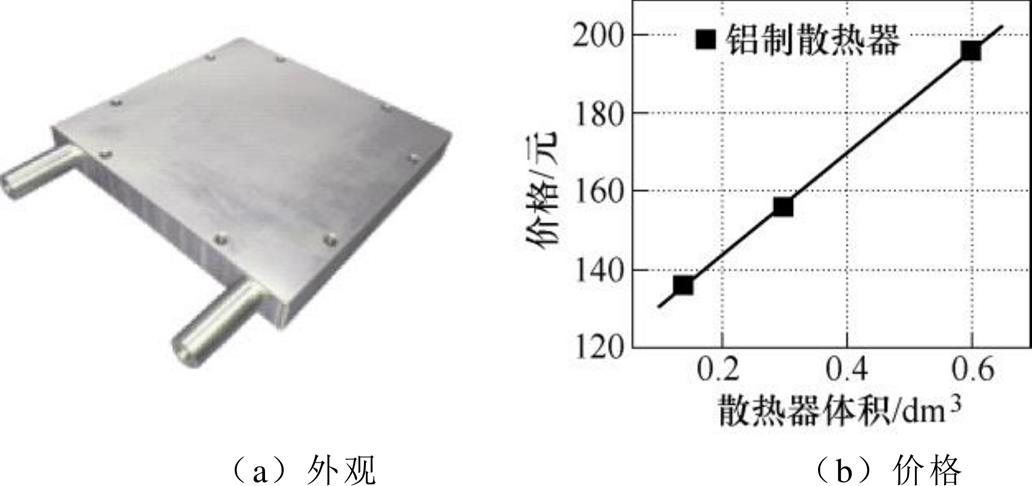
图10 水冷板外观和价格
Fig.10 Appearance and unit price of water cooling plate
变流器DC-link电容既可以采用电解电容，也可以用薄膜电容。虽然电解电容单位体积电容量更高，能达到更高的功率密度，但比薄膜电容更大的等效串联电阻（Equivalent Series Resistance, ESR）和泄漏电流又会产生更大的损耗，而电容器温升每提高5℃，其寿命将减小50%。因此，综合考虑，本文选用薄膜电容，则满足纹波电流约束的最小电容值[31]可表示为
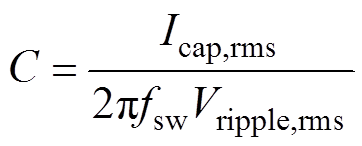（16）式中，Icap,rms为纹波电流有效值；Vripple,rms为母线电压纹波有效值。
对于驱动永磁电机的逆变器（功率因数约为1）而言，最恶劣工况下DC-link电容承受的电流应力[32]为
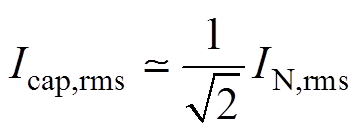（17）式中，IN,rms为变流器输出相电流的基波有效值。实际上，电机输出转矩越大，就需要越大的电流。因此，IN,rms[33]可表示为
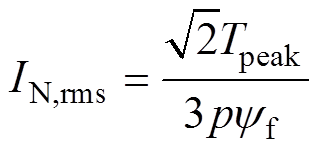（18）
式中，Tpeak为电机峰值转矩；yf为永磁体产生的磁链幅值。
对薄膜电容而言，其泄漏电流可忽略不计，则电容损耗Pdis,cap可表示为
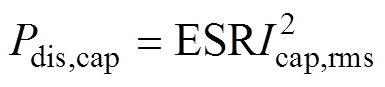（19）式中，ESR为电容等效串联电阻。进一步地，电容内核温升DTcap可表示为
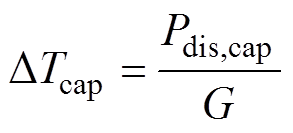（20）
式中，G为等效热导系数（可从电容数据表中获得）。
此外，统计结果表明，薄膜电容器寿命由其内核温升和纹波电流决定[34]，则
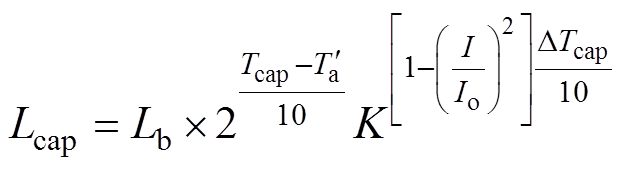（21）式中，Lcap为电容使用寿命；Lb为最高温度下的电容寿命；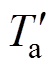
和DTcap分别为电容的、环境温度和内核温升；I为实际的纹波电流；Io为参考纹波电流；K为常量（一般取2或4）。
由于薄膜电容的体积与其电容量呈线性关系，为了使电容的选择具有一般性，本文采用的是TDK公司的B3267x系列小容量电容器。根据式（17）和式（18），可计算得到变流器最恶劣工况下流经DC-link电容器的最大纹波电流为46.82A。以开关频率8.5kHz为例，需要12只B32678G8156K电容并联。那么，由于电流分流效应，每只电容的损耗只有0.06W，引起的温升约为0.42℃，其对变流器的效率和寿命影响很小。因此，出于简化的目的，本文暂时不考虑DC-link电容对变流器损耗的影响，也不考虑电容寿命对变流器的影响，而只考虑其成本因素。
图11为TDK公司的金属化聚丙烯薄膜电容器的外观和单价，从图中可以看出，电容价格与其电容量成线性关系，则
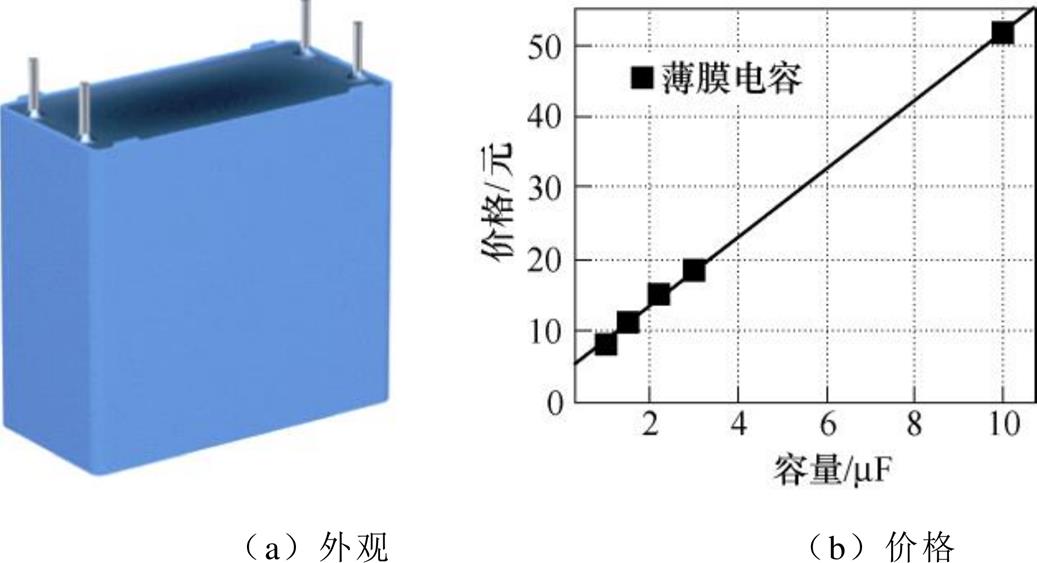
图11 薄膜电容器B3267x
Fig.11 Film capacitor B3267x
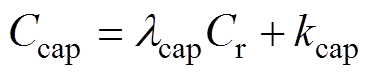（22）式中，lcap为单位电容成本；Cr为电容容量；kcap为常数，随电容生产工艺而不同。其拟合数值见表4。
变流器运行参数及约束条件见表5，根据图3中的优化过程和表5中列出的约束，可以获得如图12所示的EV变流器的可行解集。下面具体分析不同设计变量对各性能指标的影响。
表5 变流器运行参数及约束条件
Tab.5 Converter’s parameters and constraints
参 数数 值 变流器参数散热器进水温度Ta/℃70 DC-link电压Udc/V560 IGBT开关频率范围fsw/kHz3～40 IGBT芯片面积范围Achip/mm250～100 约束条件DC-link纹波电压Δudc(%)2.5 IGBT最大结温Tjmax/℃150
从图12中可以明显看出，变流器的能量损耗随开关频率fsw增加而增长，芯片面积Achip增大导致结温升高，IGBT寿命下降。然而，单位成本不一样，其随着开关频率的增大先减小后增加。与能量损耗和IGBT寿命相比，成本的变化规律复杂一点。当开关频率较低时（小于10kHz），成本快速下降至最小值；而当频率较高时，成本以较低的增长速率增长。造成这种现象主要是因为DC-link电容和水冷器的成本相互冲突。当频率较低时，IGBT损耗小，结温低，所需要的散热器成本就低。但是根据式（16）可知，更低的开关频率需要更大的电容来吸收直流母线纹波电压，造成电容的投资增大。与散热器比，薄膜电容的成本要更高些，因此开关频率较低时，变流器成本变化幅度较大。相反，随着频率增大，水冷器和电容的成本相互抵消，使得总成本变换缓慢。此外，开关频率较大时，需要一定的电容量来保证母线电压满足纹波约束条件，但却要求散热器的体积越来越大，导致总成本不断增加。
图12 EV变流器可行解集
Fig.12 The feasible solution set of EV converters
从图12还可以看出，芯片面积Achip对变流器损耗的影响微乎其微，但对成本和寿命影响较大。芯片面积每增加20mm2时，变流器寿命约增加2～3倍，成本约增长12%。当芯片面积较大时，IGBT结-壳间的热阻较小，那么同等条件下芯片的结温平均值和变化幅值均会变小，致使IGBT损伤较低、寿命变长，所以面积对变流器能量损耗影响较小。然而，IGBT模块的成本与面积近似地呈线性关系，所以变流器成本受芯片面积影响较大。
不同设计变量（开关频率fsw和芯片面积Achip）对变流器三个性能指标（ELPK、MDFF和CPW）的影响如图13所示，实线表示正比关系，虚线表示反比关系。从图中可以看出，指标ELPK与变量Achip成反比、与fsw成正比，指标MDFF与Achip成正比、与fsw成反比，而指标CPW受两变量的影响要复 杂些。
图13 设计变量与目标函数间的关系
Fig.13 Relationships between decision variables and objective functions
根据优化流程得到EV变流器的Pareto前沿如图14所示。首先，从图中可以看出，当MDFF较小及ELEK较大时，CPW可以取得更低。从前述分析（见图13）可知，增加开关频率或降低芯片面积都使得单位成本更低，但同时损耗会增加，导致ELEK增大，MDFF减小。其次，ELEK大于0.003kW·h/km时，CPW变化缓慢。这主要是因为更高的半导体损耗需要更昂贵的散热系统，这在很大程度上抵消了电容或芯片面积减小所带来的成本下降。
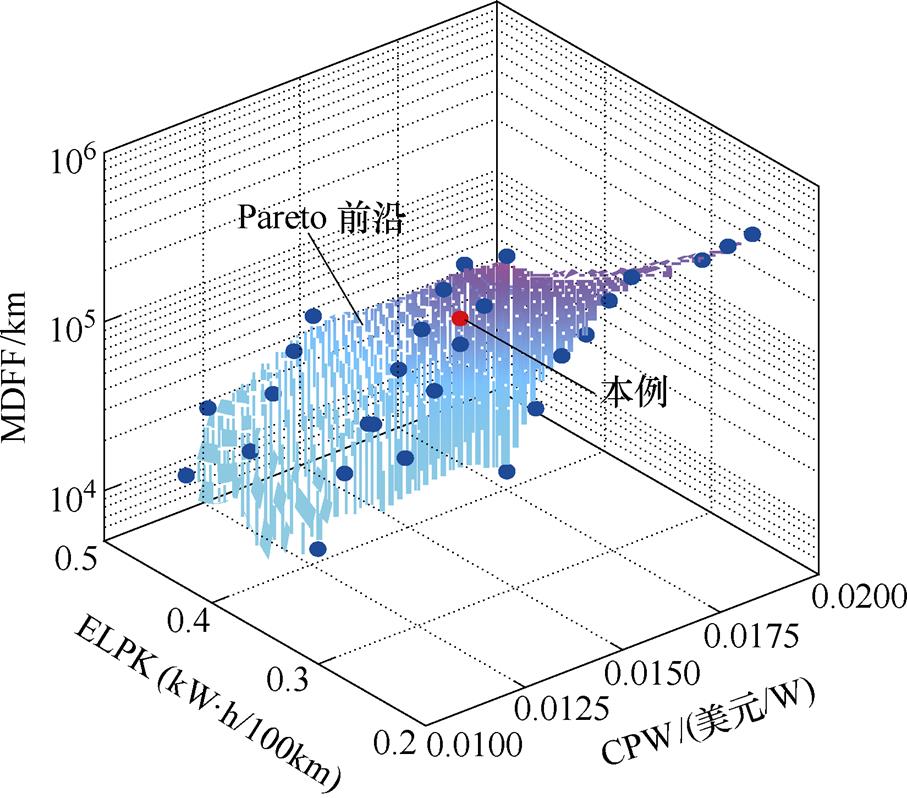
图14 EV变流器的Pareto前沿
Fig.14 Pareto front of EV converters
此外，从图14可知，EV变流器的设计存在多个最优解。为了从中选出最佳的设计方案，本文采用分层优化方法。该方法的基本思想是按重要性排序对目标函数进行排序。例如，三个性能指标ELPK、MDFF和CPW可以按优先级从高到低排序：MDFF→ELPK→CPW，该排序是基于可靠性＞效率＞成本的原则。
假如首先要求EV变流器的MDFF g＞400 000km及ELPK e ＜0.27kW·h/100km[13, 35]，然后考虑使EV变流器成本最小。详细设计过程如下：首先判断要求的性能指标g＞400 000km和e＜0.27kW·h/100km的合理性，如果它们在Pareto前沿之外，不存在最佳设计方案可以满足当前的约束条件；否则，存在最佳设计。从图14中可以很容易地发现，g＞400 000km，e ＜0.27kW·h/100km在Pareto内侧，则从Pareto前沿选出所有满足g＞400 000km和e＜0.27kW·h/100km的解。然后，两两之间相互比较，选出单位成本最小的解，即图14中所示的点（g=432 054km，ε= 0.268 8kW·h/100km，s =78.4元/kW，其设计变量开关频率fsw=8.5kHz，芯片面积Achip=76mm2），就是满足当前性能指标要求和约束的最优设计方案。
根据设计方案选取的变流器元件清单见表6，制造了一个22kW的EV变流器样机，如图15所示。实验测试平台如图16所示，其中IGBT结温通过其模块内部自带温敏电阻（Negative Temperature Coefficient, NTC），通过DSP进行AD转换和处理计算得到；水冷散热器温度采用K型热电偶和温度记录仪（TC08）测量；热交换器由水泵（最大流速12dm3/min）和带风扇的换热器组成，散热器温度可以通过调节风扇和水泵电压（即调节转速）来保持恒定70℃。
此外，补充说明以下几点：①为了和理论计算对比，实验原型的体积不是实物最大占用空间的体积，而是各部分（电容、散热器和模块）体积的直接累加；②实验选用的IGBT为FS75R12KT4，其芯片面积为70.3mm2，是优化芯片面积为76mm2的最近选择；③DC-link电容的最优值为186mF，实验选取了12个15mF薄膜电容并联构成一个180mF的电容器。理论值与实验值的对比见表7，CPW和功率密度均近似但略低于理论计算，是由于样机中的IGBT和电容参数都要小于理论值。进一步，各元件的成本和体积占比如图17所示，其中，总成本Ctot= 1 725.5元，总体积Vtot=1.683dm3。从图中可以看出，电容器占EV变流器总体积和成本的绝大多数，减小电容容量和体积是未来的重要工作。
表6 变流器元件清单
Tab.6 Bill of components of converter prototype
型号数量 IGBTFS75R12KT41 薄膜电容B32678G8156K (15mF, 875V)12 水冷散热板/mm长×宽×高(150×100×20)1 驱动电路Concept2BB0108T3
图15 实验样机实物图
Fig.15 EV converter prototype
图16 测试平台
Fig.16 Experimental platform
表7 优化设计与实验比较
Tab.7 Comparisons of the optimization design and converter prototype
参 数理论值实验值 开关频率fsw/kHz8.58.5 芯片面积Achip/mm27670.3 电容C/mF186180 体积Vtot/dm31.6831.631 总成本/元1 725.51 647.3 CPWs/(元/kW)7875 功率密度h/(kW/dm3)13.113.5
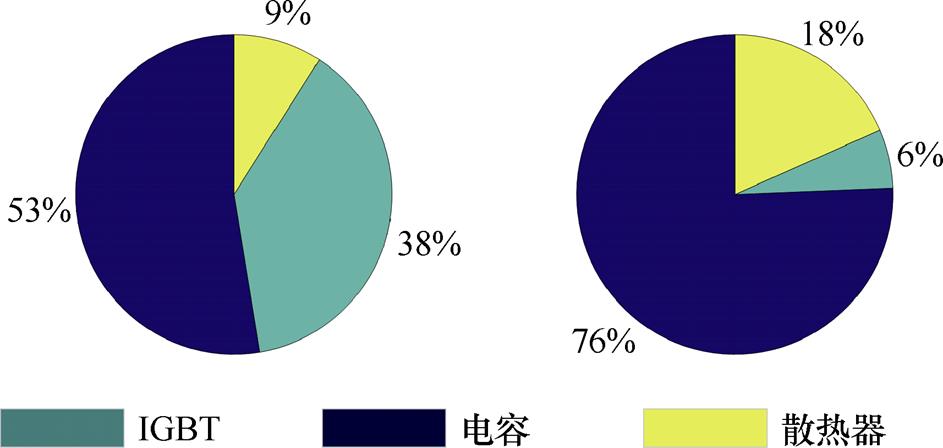
图17 变流器各元件成本和体积的占比
Fig.17 Proportions of cost and volume of the converter
表7验证了CPW指标的正确性。其他两个性能指标中，MDFF这个指标为变流器的寿命。变流器采用薄膜电容，其温升很小、寿命很长，因此寿命是指IGBT的寿命（不考虑连接件）。对于IGBT的寿命，有加快老化实验方法和仿真方法，其中加速老化实验包括温度循环和功率循环（即固定结温和结温波动，或固定功率和功率波动）两种，而变工况下IGBT的寿命，业内通用的是仿真方法，即根据仿真得到的温度曲线进行雨流计数后统计实现。另一指标ELPK为行驶工况下变换器能耗指标，需要时变负载进行测试。实验室不具备大功率时变负载，但是，能量损耗可以通过损耗实验进行间接验证，如果不同开关频率下，理论计算和实验的损耗基本吻合，那么能量只是多了一个时间变量，结果也将吻合。由于逆变器的绝大部分损耗都来源于IGBT，为验证开关频率对IGBT损耗的影响，测试了不同开关频率下的系统损耗和IGBT结温。实验参数见表8，实验结果如图18所示，与图12a的能量损耗率变化趋势一致。此外，理论计算和实验结果得到的数据基本吻合，损耗最大误差均不超过8%，结温最大误差不超过3%，证明了采用式（8）进行损耗分析的正确性。
表8 实验参数
Tab.8 Parameters of the experiments
参 数数 值 母线电压/V200 输出电流有效值/A20 功率因数0.91 输出频率/Hz200
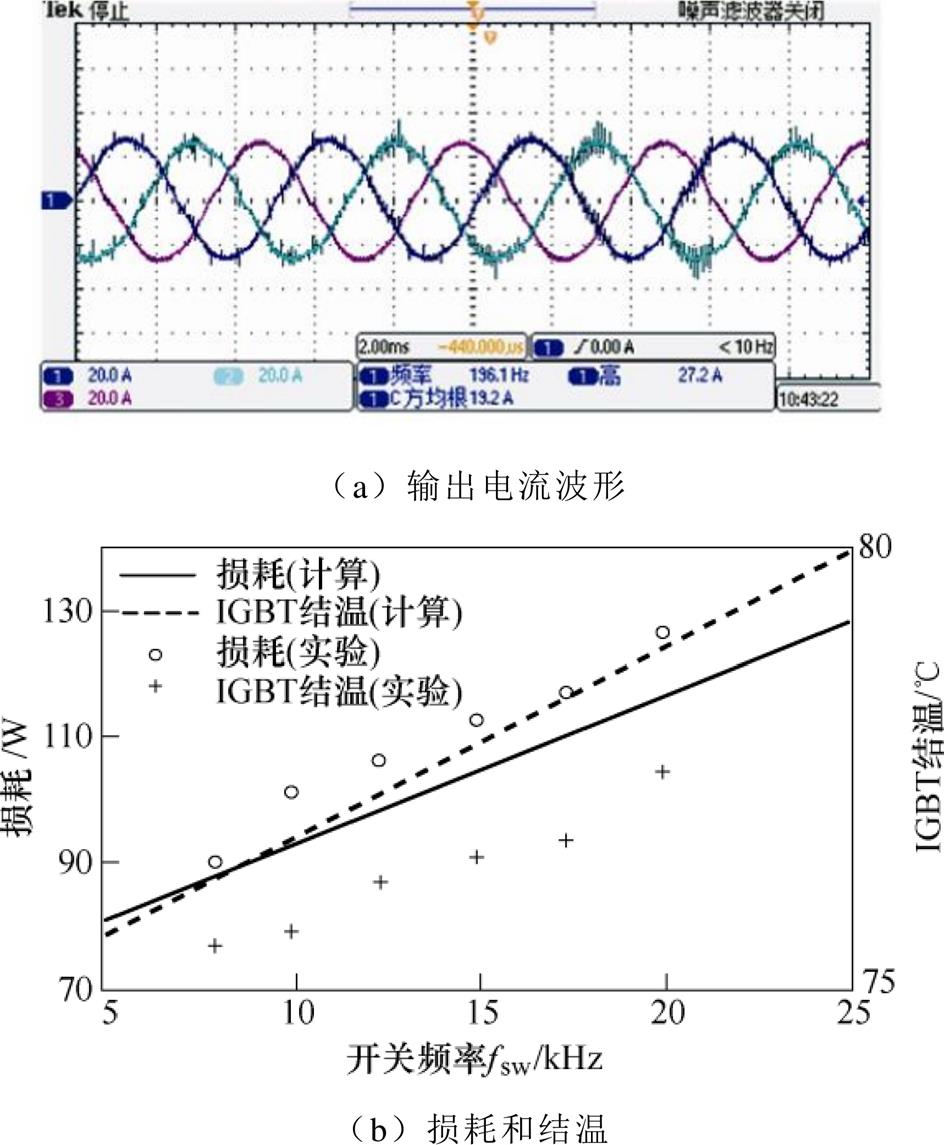
图18 实验结果
Fig.18 Experimental results
本文提出一种EV变流器的多目标优化设计方法，以寻找长时间工作下最合适的IGBT和开关频率。以开关频率和芯片面积作为设计变量建立EV变流器的三个评价函数，研究了目标函数与设计变量之间的关系，并基于Pareto最优理论实现能量损耗、成本和寿命之间的最佳折中。基于该方法，可以在满足设计要求的前提下获得最佳的设计方案，使得EV变流器满足效率和可靠性要求的同时成本最小。最后，实验验证了该方法的有效性。在优化设计过程中，也存在一些不足：一是对变流器性能有较大影响的IGBT驱动电路部分没有包括在优化设计中；二是尚未考虑不同元件（如IGBT和电容器）之间的热耦合作用。这些不足将会在未来的工作中进一步探讨和研究。
参考文献
[1] Zhou Heliang, Wei Feng, Sun Liqing. Development status of electric vehicles[J]. Journal of Asian Electric Vehicles, 2009, 2(1): 531-534.
[2] International energy agency. Global EV outlook 2017[DB/OL]. https://webstore.iea.org/global-ev- outlook-2017, 2017-6-6.
[3] 刘庆, 刘和平, 刘平, 等. 电动汽车用异步电动机低速转矩最大化[J]. 电工技术学报, 2017, 32(24): 30-41.
Liu Qing, Liu Heping, Liu Ping, et al. Torque maximization about electric vehicle induction motor at low speed[J]. Transactions of China Electro- technical Society, 2017, 32(24): 30-41.
[4] 王琪, 孙玉坤, 罗印升. 混合动力电动汽车的复合电源功率分配控制策略[J]. 电工技术学报, 2017, 32(18): 143-151.
Wang Qi, Sun Yukun, Luo Yinsheng. A power distribution control strategy of hybrid energy storage system in hybrid electric vehicles[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 143- 151.
[5] 王莉娜, 邓洁, 杨军一, 等. Si和SiC功率器件结温提取技术现状及展望[J]. 电工技术学报, 2019, 34(4): 703-716.
Wang Lina, Deng Jie, Yang Junyi, et al. Junction temperature extraction methods for Si and SiC power devices—a review and possible alternatives[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(4): 703-716.
[6] Wang Huai, Liserre M, Blaabjerg F, et al. Transi- tioning to physics-of-failure as a reliability driver in power electronics[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2014, 2(1): 97-114.
[7] Chen Dezhi, Kwon B, Bai Baodong. Selection of IGBTs for controlling rectifier and inverter based upon a novel analytical approach for loss calculation[C]//International Conference on Power Electronics and ECCE Asia, Seoul, South Korea, 2015: 1109-1115.
[8] Song Shoujun, Liu Weiguo, Schaefer U. Detailed power converter design for a 30kW switched reluctance starter/generator used in aircraft[C]// European Conference on Power Electronics and Applications, Barcelona, Spain, 2009: 1-10.
[9] Gong Guanghai, Heldwein L, Drofenik U, et al. Comparative evaluation of three-phase high-power- factor AC-DC converter concepts for application in future more electric aircraft[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 727-737.
[10] Josep B, Alfonso S, Orlandi A, et al. EMI reduction in switched power converters using frequency modulation techniques[J]. Converter Technology & Electric Traction, 2006, 47(3): 569-576.
[11] Besnerais J, Lanfranchi V, Hecquet M, et al. Characterization and reduction of audible magnetic noise due to PWM supply in induction machines[J] IEEE Transactions on Industrial Electronics, 2010, 57(4): 1288-1295.
[12] Waffler S, Preindl M, Kolar W. Multi-objective optimization and comparative evaluation of Si soft-switched and SiC hard-switched automotive DC-DC converters[C]//Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 2009: 3814- 3821.
[13] Whaling C L. Electrical and electronics technical team roadmap[DB/OL]. https://www.energy.gov/sites/ prod/files/2014/03/f13/ape032_whaling_2013_o.pdf, 2014-3-13.
[14] Biela J, Kolar W, Stupar A, et al. Towards virtual prototyping and comprehensive multi-objective opti- misation in power electronic[C]//Power Conversion and Intelligent Motion Conference Europe (PCIM), Nuremberg, Germany, 2010: 1-23.
[15] Ngatchou P, Zarei A, EI-Sharkawi A. Pareto multi- objective optimization[C]//International Conference on Intelligent Systems Application to Power Systems, Arlington, USA, 2005: 6-10.
[16] Deb K. Multi-objective optimization[M]. 2nd ed. Berlin: Springer, 2014.
[17] Niazi A, Dai S, Balabani S, et al. Product cost estimation: technique classification and methodology review[J]. Journal of Manufacturing Science, 2006, 128(2): 563-575.
[18] Adinolfi G, Graditi G, Siano P, et al. Multi-objective optimal design of photovoltaic synchronous boost converters assessing efficiency, reliability, and cost savings[J]. IEEE Transactions on Industrial Infor- mation, 2015, 11(5): 1038-1048.
[19] Boillat O, Krismer F, Kolar W. Design space analysis and r -h pareto optimization of LC output filters for switch-mode AC power sources[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(12): 6906- 6923.
[20] Burkart M, Kolar W. Comparative life cycle costs analysis of Si and SiC PV converter systems based on advanced h-r-s multi-objective optimization techni- ques[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4344-4358.
[21] Burkart M, Kolar W. Comparative h-r-s pareto optimization of Si and SiC multi-level dual active bridge topologies with wide input voltage range[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5258-5270.
[22] Schaltz E. Electric vehicles-modelling and simu- lations[M]. Aalborg: Aalborg University, 2011.
[23] Shen Yanfeng, Wang Huai, Yang Yongheng, et al. Mission profile-based sizing of IGBT chip area for PV inverter applications[C]//International Sympo- sium on Power Electronics for Distributed Generation Systems, Vancouver, Canada, 2016: 1-8.
[24] Wintrich A, Nicolai U, Tursky W, et al. Application manual power semiconductors[M]. Nuremberg: ISLE Verlag, 2011: 100-129.
[25] 汪波, 罗毅飞, 张烁, 等. IGBT极限功耗与热失效机理分析[J]. 电工技术学报, 2016, 31(12): 135-141.
Wang Bo, Luo Yifei, Zhang Shuo, et al. Analysis of limiting power dissipation and thermal failure mechanism[J]. Transactions of China Electro- technical Society, 2016, 31(12): 135-141.
[26] Bryant T, Mawby A, Palmer R, et al. Exploration of power device reliability using compact device models and fast electro-thermal simulation[J]. IEEE Transa- ctions on Industrial Applications, 2008, 44(3): 894- 903.
[27] 赖伟, 陈民铀, 冉立, 等. 老化实验条件下的IGBT寿命预测模型[J]. 电工技术学报, 2016, 31(24): 173-180.
Lai Wei, Chen Minyou, Ran Li, et al. IGBT lifetime model based on aging experiment[J]. Transaction of China Electrotechnical Society, 2016, 31(24): 173-180.
[28] Qin Sun, Dui Hongna, Fan Xueling. A statistically consistent fatigue damage model based on Miner’s rule[J]. International Journal of Fatigue, 2014, 69: 16-21.
[29] Drofenik U, Laimer G, Kolar W. Theoretical con- verter power density limits for forced convection cooling[C]//Proceeding of the International PCIM Europe Conference, Nuremberg, Germany, 2005: 608-619.
[30] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 教育出版社, 2006.
[31] Terzulli G. Evolution of power capacitors for Electric Vehicles[DB/OL]. http://www.avx.com/docs/techinfo/ EvolutionPowerVehicles.pdf. 2018-10-11.
[32] Kolar W, Round D. Analytical calculation of the RMS current stress on the DC-link capacitor of voltage- PWM converter systems[J]. IEE Proceedings-Electric Power Applications, 2006, 153(4): 535-543.
[33] Pillay P, Krishnan R. Modeling, simulation, and analysis of permanent-magnet motor drives. Part I: the permanent-magnet synchronous motor drive[J]. IEEE Transactions on Industrial Applications, 1989, 25(2): 265-273.
[34] Wen Xuhui, Hu Wei, Fan Tao, et al. Lifetime model research of motor drive system for electric vehicles[C]//2007 International Conference on Electrical Machines and Systems (ICEMS), Seoul, South Korea, 2007: 129-132.
[35] Wen Huiqing, Xiao Weidong, Wen Xuhui, et al. Analysis and evaluation of DC-link capacitors for high-power-density electric vehicle drive systems[J]. IEEE Transactions on Vehicular Technology, 2012, 61(7): 2950-2964.
Selections of IGBTs and Switching Frequency of the Electric Vehicle Converter Based on Multi-Objective Optimization
Abstract The selection of IGBTs is the primary and most important issue in the design stage of power converters, and plays an important role in converter’s efficiency, reliability and cost. However, IGBTs and switching frequency are always chosen approximately and empirically, and there is no clear theoretical basis so far. To solve this problem, a novel optimized design method of EV converters is proposed in this paper. First, three evaluation functions related to energy loss, lifetime and cost are established based on long term driving cycles. Then, the Pareto solution sets of two variables of IGBTs and switching frequency are obtained by the designed multi-objective optimization process. Last, an optimal solution is selected by using hierarchical analysis method and verified by experiments.
keywords：Electric vehicles converter, multi-objective optimization, reliability, cost
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190486
罗 旭 男，1990年生，硕士研究生，研究方向为电动汽车车变流器及其控制方法。E-mail: epxluo@mail.scut.edu.cn
王学梅 女，1972年生，博士，教授，研究方向为电力电子变流器的可靠性及控制方法。E-mail: epxmwang@scut.edu.cn（通信作者）
收稿日期2019-04-24
改稿日期 2019-09-04
国家自然科学基金资助项目（51577074）。
（编辑 崔文静）