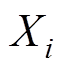 与
与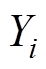 的斯皮尔曼等级相关系数计算公式为[21]
的斯皮尔曼等级相关系数计算公式为[21]摘要 目前对低压电器电寿命预测的研究多集中在剩余电寿命预测,然而预测预期电寿命更能有效指导产品的使用与维护,并且提高系统服役期的可靠性。交流接触器初态特征在一定程度上能够反映个体电寿命的长短,由此提出一种基于粗糙集与证据理论的交流接触器预期电寿命预测方法。首先采用粗糙集理论并结合相关计算经二次筛选获取关键初态特征,然后利用主客观综合赋权法建立关键初态特征权重集,并基于属性条件密度建立验证样本关键初态特征的匹配度表,之后利用二者构建独立证据,运用证据理论进行证据融合,决策验证样本个体预期电寿命等级。经实测数据验证,在小子样情况下,该方法可定性评估交流接触器个体预期电寿命,预测效果良好。
关键词:交流接触器 粗糙集理论 属性条件密度 证据理论 寿命预测
交流接触器是一种广泛使用的低压控制电器,主要用于远距离频繁接通和开断交流主电路以及大容量控制电路,对其寿命进行预测尤为重要。目前在低压电器电寿命预测的研究中,对剩余电寿命预测的研究较多[1-4]。但考虑到在工矿、交通运输、军事、航天等领域中,因交流接触器工作模式、工作环境、操作频率等不同,一般要求交流接触器电寿命达到数万次至几十万次。特别是相关行业里某些可靠性要求高、不易修复的系统,所采用的交流接触器不能随意更换,因而交流接触器个体电寿命须达到一定范围。若交流接触器提前退出工作状态,将直接影响系统的可靠运行,可能会造成严重的安全问题及经济损失。因此若在交流接触器出厂时就能实现交流接触器个体预期电寿命的准确预测,将便于交流接触器的使用和维护,对提高系统的安全运行水平具有重要意义。
当前,低压电器预期寿命预测的方法可分为两类:一类是基于抽样检测理论,根据样本的寿命数据推测整体的寿命分布[5]以及与寿命有关的可靠性特征量,如平均寿命、可靠寿命等。这类方法能够得到一批产品整体的寿命指标,但是在实际的生产过程中,因产品材料和制造工艺无法完全一致及人为因素的影响,同一批次的产品个体寿命存在一定的差别,表征整体寿命的指标无法准确反映某一个体的准确寿命情况。另一类方法是根据产品个体的性态参数推测其寿命,此类方法建立在产品个体的参数变化与寿命的内在关联之上,可以体现同一批次下不同产品个体的寿命差别,故其适用于产品个体的寿命预测。
预测寿命的性态参数可分为两类:性能退化特征和寿命初态特征。根据产品个体的性能退化特征推测产品寿命属于在线预测,当前的研究大多集中于基于回归分析、灰色模型等数学方法建模的预测。文献[6]将超程时间数据划分为多个区间,求得各区间平均超程时间作为测试集,在此基础上建立超程时间回归模型预测继电器寿命,并通过参数动态更新以提高预测准确度;文献[7]以超程时间为性能退化特征,采用灰色模型拟合超程时间的变化趋势,以超程时间失效阈值对应的开断次数作为安全型继电器的预测寿命。这类预测方法所需数据量较大,计算过程较复杂,不太适用于成本较低的产品。根据产品个体的寿命初态特征推测产品寿命属于离线预测,所需的数据量少,计算过程相对简单,在寿命预测后不影响产品的正常使用,因此通过产品的寿命初态特征预测预期寿命更具实用价值。当前已有文献从定性、定量的角度实现了继电器预期寿命的预测。文献[8]研究了吹弧磁场磁通密度和触点分断速度对继电器电寿命的影响,建立了前期的磁通密度、分断速度与继电器电寿命之间的回归模型,可用于高压直流输电继电器电寿命的定量预测。文献[9]根据继电器初始接触电阻定义了单个性能评价指标,建立单个性能评价指标与寿命的数学关系模型,定量评估继电器个体寿命,但由于初态特征与寿命之间关系复杂,仍需全面研究初态特征与个体寿命之间的定量关系,从而进一步提高预测准确度。文献[10]分析了继电器生命初态信息与其寿命的关联性,得到了初态信息与寿命之间的联系,提出了基于粗糙集理论的预测方法,利用个体间特征的匹配程度定性预测继电器试品的预期寿命,实用性较强。定性评估预期寿命实质上是一种对预期寿命的不确定性推理,即从带有模糊性、随机性、不确定因素的初态信息出发,在推理过程中运用不确定性知识,最终推理出具有一定程度不确定性的预期寿命等级。
不确定性推理的流程一般分为两步:首先在初始信息中筛选关键指标,之后基于关键指标结合相关不确定性推理方法推导结论。初始信息中有时存在较多冗余信息,使得运算过程较为复杂,推理结果准确度不高,因此首先要在初始信息中筛选关键指标,为后续的不确定性推理奠定基础。粗糙集理论的约简功能,可以在保持特征指标判别能力不变的情况下,删除其中不相关或不重要的指标,减少计算复杂度,在其他领域已实现较广泛的应用[11-13]。
在获得关键指标的基础上,根据相关方法进行不确定推理,最终推理出具有一定不确定性但基本合理的结论。常用不确定性推理方法包括可信度方法[14]、贝叶斯方法[15]、粗糙集理论[16]、证据理论[17-18]等。在处理不确定性信息上,证据理论比其他方法更加灵活,可以在不同层次上通过一定的证据合成方法对不同的证据体进行融合分析,从多方面给出对不确定性问题的描述,该方法处理过程简单,能区分“不确定”与“不知道”的差异,因此在不确定推理方面应用较为广泛。
粗糙集和证据理论的联合应用可省略粗糙集单一运用时规则提取的复杂运算,在一定程度上减少了计算量,同时可实现多属性数据的融合,更好地对已有数据之间的差异进行区分。文献[19]利用粗糙集的约简功能来优化设备技术状态评估指标,之后运用证据理论评估汽轮鼓风机技术状态类别。文献[20]利用粗糙集减小故障诊断系统的属性维数,再采用证据理论融合约简后的测试结果,从而决策机载高度表收发机故障类别。
综上,本文从定性角度评估交流接触器预期电寿命,利用斯皮尔曼等级相关系数研究交流接触器特征参量和电寿命之间的内在关联,为预测方法的建立奠定基础。之后建立一种基于粗糙集与证据理论定性预测交流接触器预期电寿命的方法。利用粗糙集理论结合相关计算筛选单类初态特征的最佳属性集,组合后二次约简筛选关键初态特征;采用关键初态特征权重集和验证样本关键初态特征的匹配度表构建证据理论的独立证据,运用Dempster组合规则进行证据组合,根据融合证据计算类概率函数值,给出预期电寿命等级的不确定性度量,决策验证样本个体的预期电寿命等级。在该预测方法的基础上,结合相关实例验证方法的有效性。
本文利用斯皮尔曼等级相关系数分析特征参量与电寿命的相关性,基于粗糙集理论、证据理论等方法建立交流接触器预期电寿命预测方法,其中涉及的主要理论与定义如下。
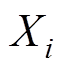 与
与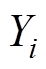 的斯皮尔曼等级相关系数计算公式为[21]
的斯皮尔曼等级相关系数计算公式为[21]
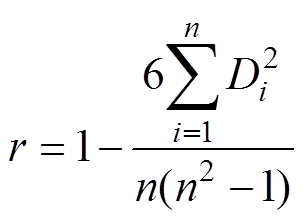 (1)
(1)
式中,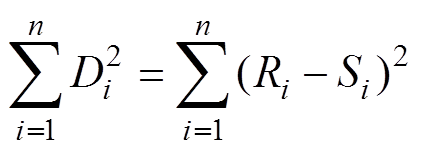 ,
,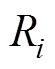 、
、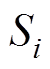 分别为
分别为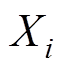 、
、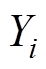 按大小或者优劣排序后的秩;
按大小或者优劣排序后的秩;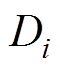 为两变量对应秩的差值;n为样本含量。
为两变量对应秩的差值;n为样本含量。
当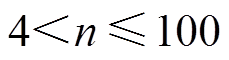 时,可通过查表进行等级相关检验。H0:
时,可通过查表进行等级相关检验。H0: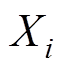 与
与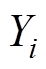 相互独立;H1:
相互独立;H1: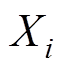 与
与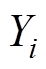 负相关,进行单侧检验。如果
负相关,进行单侧检验。如果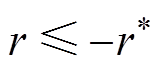 ,则拒绝H0,即
,则拒绝H0,即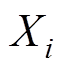 与
与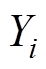 存在负相关关系,其中,
存在负相关关系,其中,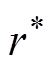 可根据显著性水平
可根据显著性水平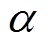 和自由度n查询等级相关系数临界值表获得。
和自由度n查询等级相关系数临界值表获得。
在粗糙集理论[10]中,知识被认为是一种对研究论域对象具有分类能力的信息。知识表达系统也称为信息系统,多元组表示的信息系统S如下:S =〈U, A, V, f 〉,其中U为研究对象的非空有限集,称为论域;A为属性的非空有限集,A=C∪D,C为条件属性,D为决策属性;V为属性值的集合,V=∪Va,Va为属性a的值域;f:U×A→V是一个信息函数,它为每个对象的每个属性赋予一个信息值: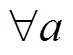 ∈A,x∈U,f(x, a)∈Va。
∈A,x∈U,f(x, a)∈Va。
设E是U上的一个等价关系,U/E表示E的所有等价类组成的集合。若R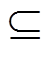 E且R≠
E且R≠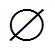 ,则∩R(即R中所有等价类关系的交集)也是一个等价关系,称为R上的不可区分关系,记为ind(R)。U/ind(R)表示与等价关系族R相关的知识。
,则∩R(即R中所有等价类关系的交集)也是一个等价关系,称为R上的不可区分关系,记为ind(R)。U/ind(R)表示与等价关系族R相关的知识。
1)上近似、下近似与正域
设U是给定论域,X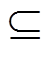 U,E是U上的等价关系族,可以得到两个与之相关的子集,即
U,E是U上的等价关系族,可以得到两个与之相关的子集,即
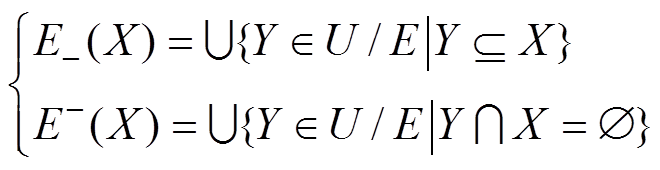 (2)
(2)式中,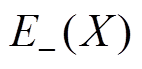 、
、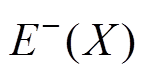 分别称为集合X的下近似集和上近似集,并有
分别称为集合X的下近似集和上近似集,并有
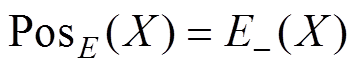 (3)
(3)
称为集合X的正域。
2)知识的约简
约简是获得与信息系统的属性全集具有相同基本集的最小属性子集。设R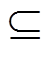 E,如果R是独立的,且ind(R)=ind(E),则R是E的一个约简。
E,如果R是独立的,且ind(R)=ind(E),则R是E的一个约简。
3)属性依赖度
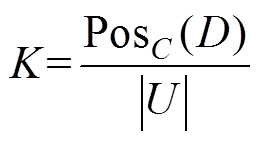 (4)
(4)属性依赖度K表达了决策属性对条件属性的依赖程度,表示在条件属性C下能够准确划分到决策类U/D的对象比率。
朴素贝叶斯分类模型可使用一种基于高斯核的核密度估计方法来计算属性条件密度P(Xj|Yi)[22],即叠加多个高斯分布来拟合概率密度函数,更接近实际情况。对于类别Yi,属性Xj的条件密度为
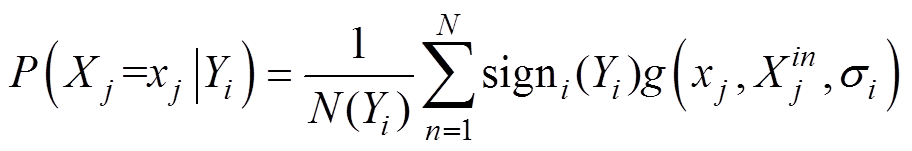 (5)
(5)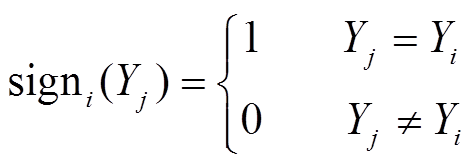 (6)
(6)
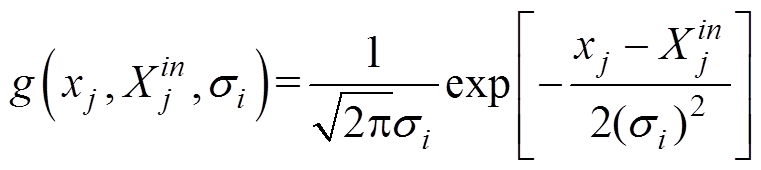 (7)
(7)
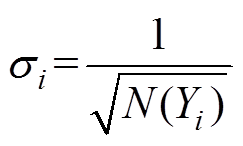 (8)
(8)式中,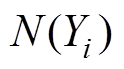 为数据集中属于类别Yi的样本数量;
为数据集中属于类别Yi的样本数量;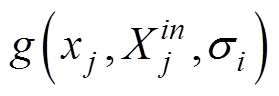 为高斯核函数,其中xj为要输入的属性值,
为高斯核函数,其中xj为要输入的属性值,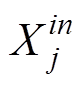 为在类别Yi中第n个样本的第j个属性值,
为在类别Yi中第n个样本的第j个属性值,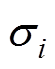 为窗口宽度参数。
为窗口宽度参数。
证据理论[23]在信息融合、模式识别及决策分析等领域已得到广泛应用,其基本概念如下。
1.4.1 基本概率分配函数、信任函数和似然函数
假设全域Z={z1, z2, , zn}为系统中所有可能发生的状态,且Z的各个元素互斥,则Z称为辨识框架。令2Z表示Z的所有子集组成的幂集,则任何一个命题A可以表达为2Z的一个子集。
, zn}为系统中所有可能发生的状态,且Z的各个元素互斥,则Z称为辨识框架。令2Z表示Z的所有子集组成的幂集,则任何一个命题A可以表达为2Z的一个子集。
设Z为辨识框架,函数m:2Z→[0, 1]称为基本概率分配函数,表示对命题A的精确信任度。对于空集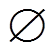 ,
,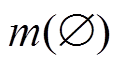 =0,对于A
=0,对于A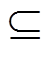 2Z,
2Z,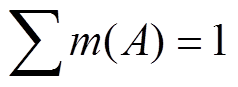 。若m(A)>0,则称命题A为该函数的一个焦元。
。若m(A)>0,则称命题A为该函数的一个焦元。
信任函数Bel:2Z→[0, 1],表示对A的全部信任。其中
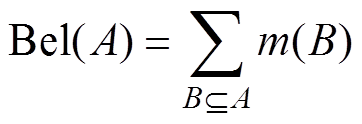 (9)
(9)似然函数Pl:2Z→[0, 1],表示对A的潜在信任。其中
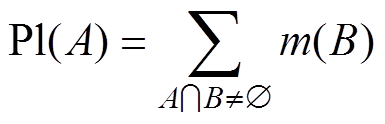 (10)
(10)
1.4.2 Dempster组合规则
设m1和m2分别是Z上的两个独立证据的概率分配函数,其对应的焦元分别为x、y。m1和m2的Dempster组合结果也是一个概率分配函数,可表示为m= m1 m2,其定义为
m2,其定义为
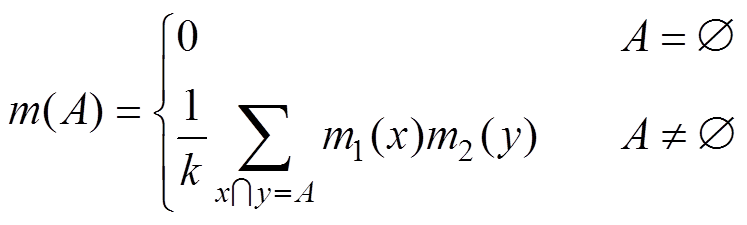 (11)
(11)式中,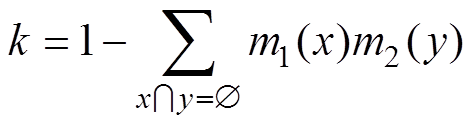 。
。
若需要合成两个以上证据时,可先结合前两个独立证据,再将Dempster组合结果同第三个证据相结合,以此类推,直到最后结果。
1.4.3 类概率函数
命题A的类概率函数为
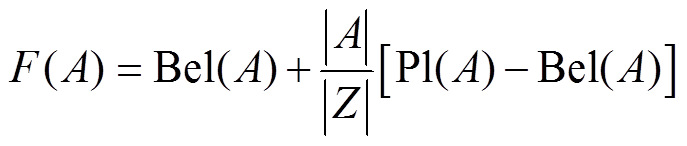 (12)
(12)式中,|A|、|Z|分别为A和Z中包含元素的个数。类概率函数可以衡量命题A的不确定性,代表了命题A成立的估计信任度。
本文选取11个H8C-12型号交流接触器作为试品,基于交流接触器电寿命试验平台,对交流接触器试品进行全寿命试验。采集交流接触器动作过程中触点的电压、电流,监测并记录这些试品随动作次数变化的特征参量。具体的试验条件见表1。
表1 电寿命试验条件
Tab.1 Electrical life test conditions
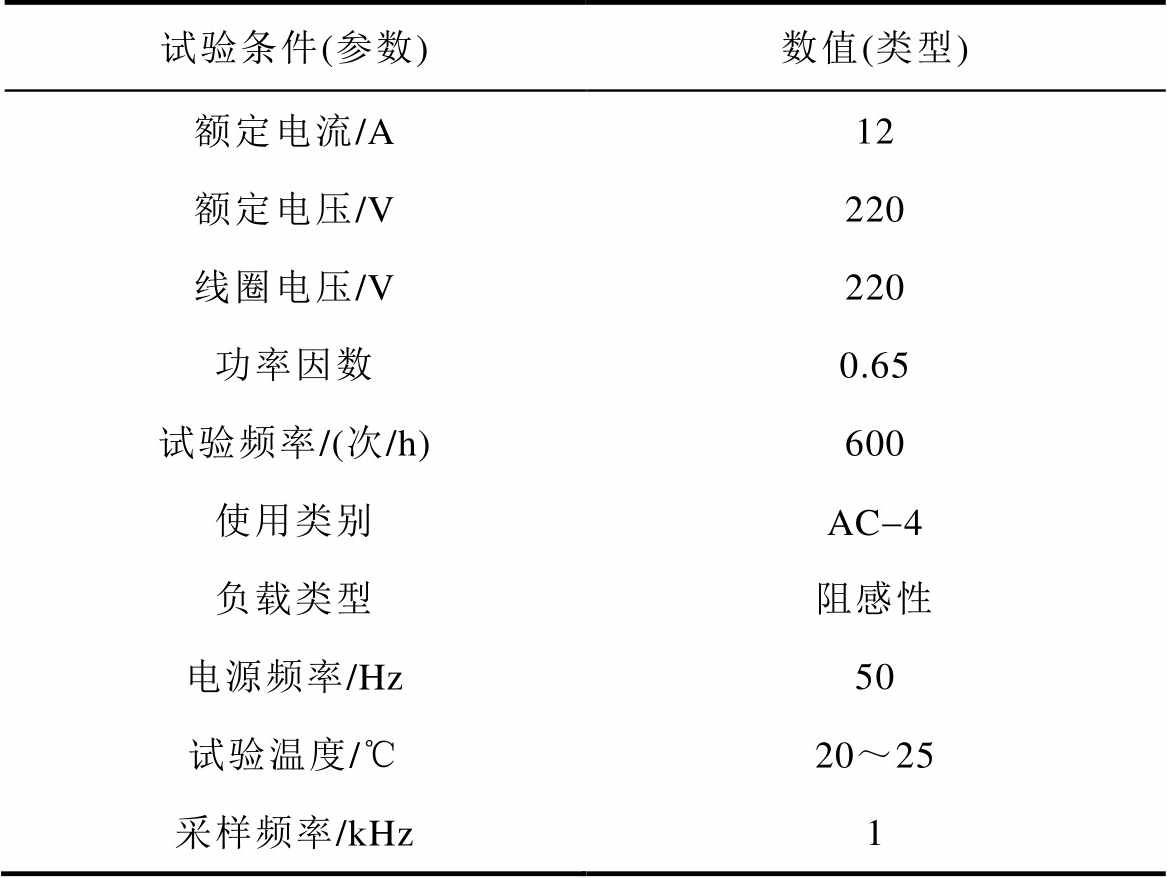
试验条件(参数)数值(类型) 额定电流/A12 额定电压/V220 线圈电压/V220 功率因数0.65 试验频率/(次/h)600 使用类别AC-4 负载类型阻感性 电源频率/Hz50 试验温度/℃20~25 采样频率/kHz1
以11个交流接触器的某相电寿命试验数据为例进行研究,提取寿命次数及其前1 000次的特征参量,研究的特征参量包括燃弧时间、燃弧能量、接触电阻、接触压降和释放电压,对前1 000次的特征参量做均值统计,统计结果见表2。
采用斯皮尔曼等级相关系数分析以上特征参量与电寿命的相关性,相关系数见表3。
对上述特征参量进行单侧检验。通过查询斯皮尔曼相关系数临界值表,获取临界值。在显著性水平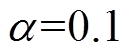 的条件下,
的条件下,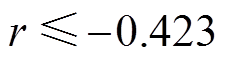 ,认为特征参量与电寿命存在负相关关系,
,认为特征参量与电寿命存在负相关关系,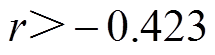 ,认为特征参量与电寿命无相关性。
,认为特征参量与电寿命无相关性。
表2 交流接触器特征参量与电寿命
Tab.2 The characteristic parameters and electrical life of AC contactor
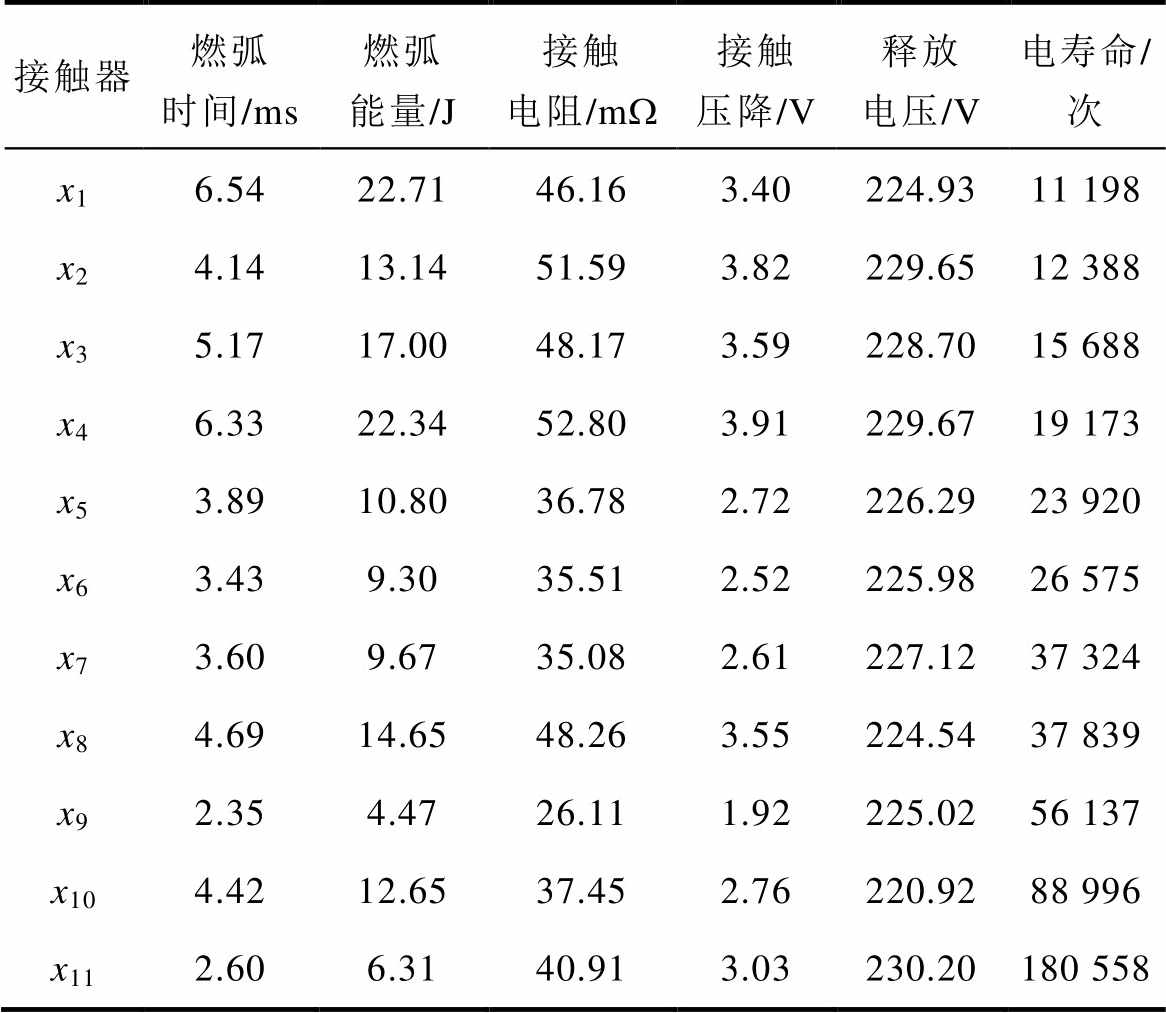
接触器燃弧时间/ms燃弧能量/J接触电阻/mW接触压降/V释放电压/V电寿命/次 x16.5422.7146.163.40224.9311 198 x24.1413.1451.593.82229.6512 388 x35.1717.0048.173.59228.7015 688 x46.3322.3452.803.91229.6719 173 x53.8910.8036.782.72226.2923 920 x63.439.3035.512.52225.9826 575 x73.609.6735.082.61227.1237 324 x84.6914.6548.263.55224.5437 839 x92.354.4726.111.92225.0256 137 x104.4212.6537.452.76220.9288 996 x112.606.3140.913.03230.20180 558
表3 特征参量与电寿命的相关系数
Tab.3 Correlation coefficient between characteristic parameters and electrical life

r燃弧时间燃弧能量接触电阻接触压降释放电压 电寿命-0.64-0.71-0.47-0.51-0.17
由上述分析可知,针对研究试品,释放电压与电寿命无相关性,燃弧时间、燃弧能量、接触电阻、接触压降与交流接触器电寿命存在负相关关系。
燃弧时间与燃弧能量有一定的相关性,接触电阻与接触压降同理。由表2数据计算燃弧时间与燃弧能量、接触电阻与接触压降的相关系数,见表4。
表4 特征参量之间的相关系数
Tab.4 Correlation coefficient between characteristic parameters

燃弧时间与燃弧能量接触电阻与接触压降 r0.990.98
由表4可知,燃弧时间与燃弧能量正相关程度较高,所包含的信息类似,因此选取其中之一作为初态信息即可,接触电阻与接触压降同理。由表3可知,燃弧能量、接触压降的相关系数绝对值比另外一组略大,因此最终选择燃弧能量、接触压降进行研究。
为了更为直观地反映燃弧能量、接触压降与交流接触器电寿命的关系,采用最小二乘一次拟合曲线拟合上述特征参量与交流接触器电寿命的总体趋势如图1所示。
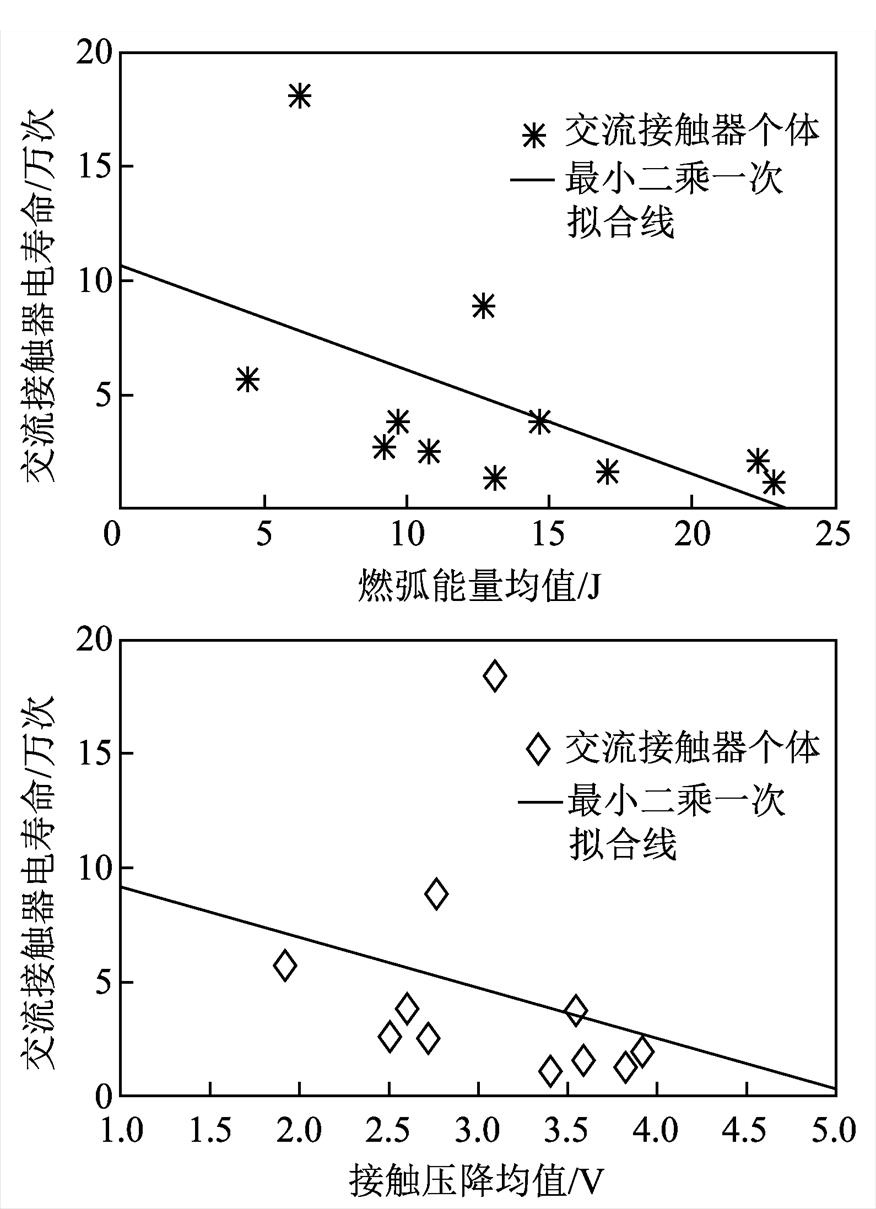
图1 特征参量与接触器电寿命拟合趋势图
Fig.1 Fitting trend diagram between characteristic parameters and electrical life of contactor
从图1的拟合趋势可知,以燃弧能量均值、接触压降均值作为初态特征,其在一定程度上可以反映交流接触器个体电寿命的长短。燃弧能量与接触压降为成本型参数,其均值越小,代表接触器初态特征表现越好。从总体趋势而言,初态特征表现较好的个体其电寿命相对较长,反之则电寿命相对较短,但也有部分个体存在一定差异。
由上述分析可知,仅以燃弧能量均值、接触压降均值作为初态特征难以全面准确地表征交流接触器电寿命的长短,因此进一步对均值进行分段处理。以200次为区间计算各参数均值,通过燃弧能量分段均值e1~e5、接触压降分段均值v1~v5更为细致地刻画出交流接触器初期的性态变化,研究燃弧能量分段均值、接触压降分段均值与交流接触器电寿命的关系,相关数据见表5和表6。
采用斯皮尔曼等级相关系数研究燃弧能量分段均值、接触压降分段均值与电寿命的关系,其相关系数见表7。
由表7可知,在显著性水平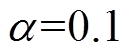 的条件下,燃弧能量分段均值、接触压降分段均值仍与电寿命存在负相关关系,但是不同的分段均值与电寿命的关联程度不同,因此筛选适当的分段均值作为预测变量能够对预期电寿命做出更为准确的预测。
的条件下,燃弧能量分段均值、接触压降分段均值仍与电寿命存在负相关关系,但是不同的分段均值与电寿命的关联程度不同,因此筛选适当的分段均值作为预测变量能够对预期电寿命做出更为准确的预测。
表5 燃弧能量分段均值与电寿命
Tab.5 Arcing energy sectional mean and electrical life
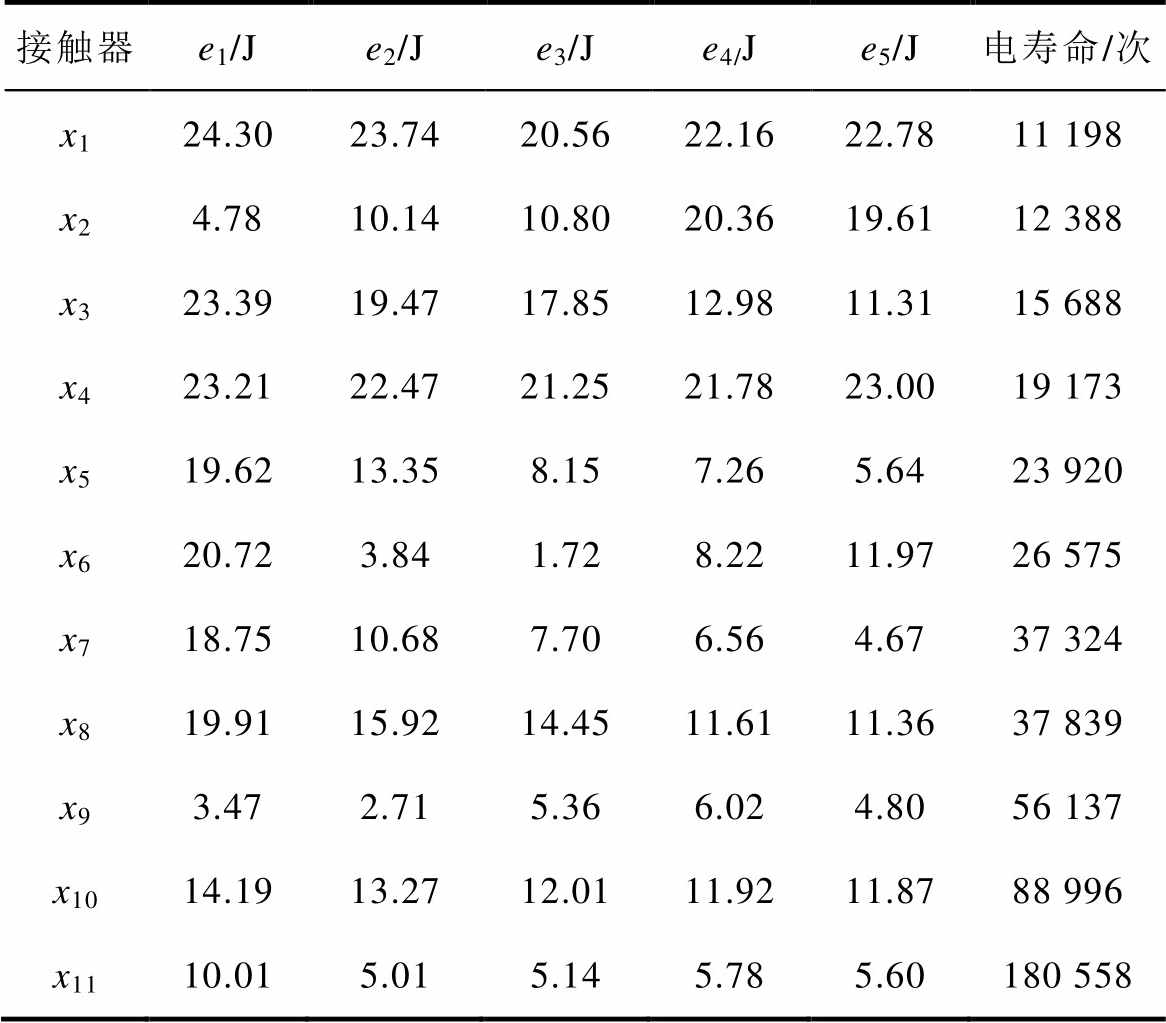
接触器e1/Je2/Je3/Je4/Je5/J电寿命/次 x124.3023.7420.5622.1622.7811 198 x24.7810.1410.8020.3619.6112 388 x323.3919.4717.8512.9811.3115 688 x423.2122.4721.2521.7823.0019 173 x519.6213.358.157.265.6423 920 x620.723.841.728.2211.9726 575 x718.7510.687.706.564.6737 324 x819.9115.9214.4511.6111.3637 839 x93.472.715.366.024.8056 137 x1014.1913.2712.0111.9211.8788 996 x1110.015.015.145.785.60180 558
表6 接触压降分段均值与电寿命
Tab.6 Contact pressure drop sectional mean and electrical life
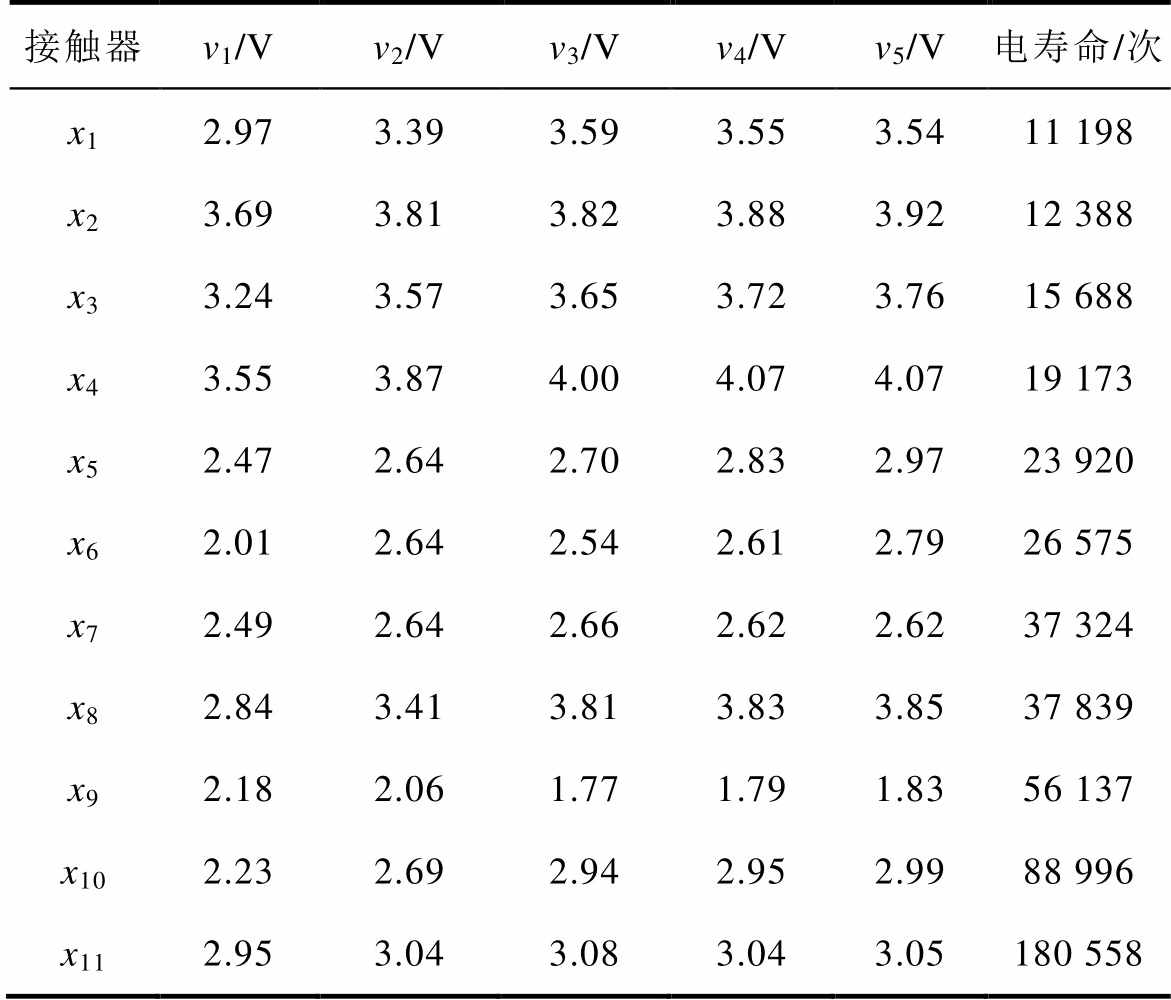
接触器v1/Vv2/Vv3/Vv4/Vv5/V电寿命/次 x12.973.393.593.553.5411 198 x23.693.813.823.883.9212 388 x33.243.573.653.723.7615 688 x43.553.874.004.074.0719 173 x52.472.642.702.832.9723 920 x62.012.642.542.612.7926 575 x72.492.642.662.622.6237 324 x82.843.413.813.833.8537 839 x92.182.061.771.791.8356 137 x102.232.692.942.952.9988 996 x112.953.043.083.043.05180 558
表7 分段均值与电寿命的相关系数
Tab.7 Correlation coefficient between sectional mean and electrical life
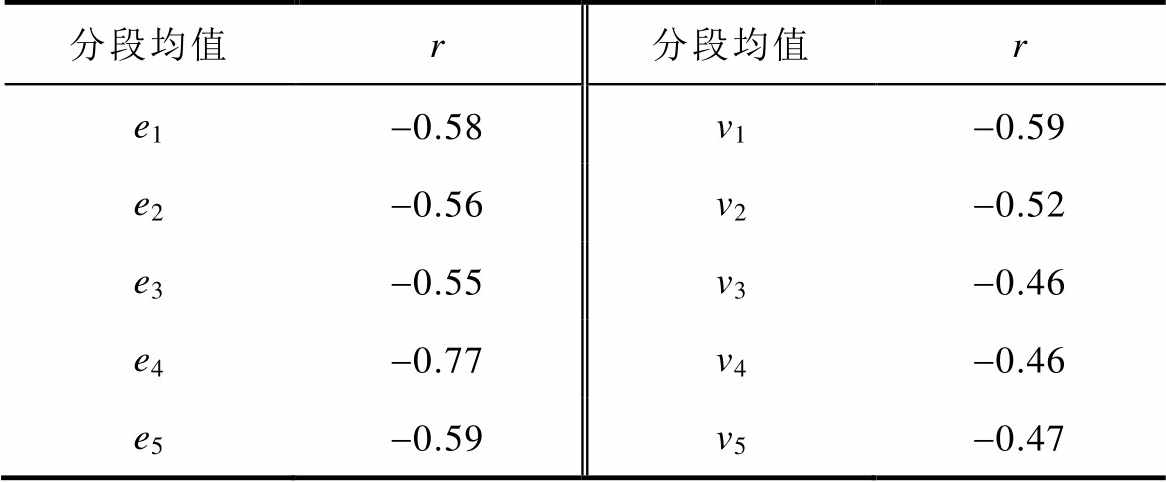
分段均值r分段均值r e1-0.58v1-0.59 e2-0.56v2-0.52 e3-0.55v3-0.46 e4-0.77v4-0.46 e5-0.59v5-0.47
交流接触器预期电寿命预测方法流程分为两大步骤:提取关键初态特征和不确定性推理预期电 寿命。
以燃弧能量分段均值e1~e5、接触压降分段均值v1~v5作为两类初态特征。由于同一类初态特征较为相近,本身可能存在信息冗余,因此采用粗糙集理论对建模样本的两类初态特征分别进行一次约简,在筛选两类初态特征各自的最佳属性集后,组合最佳属性集进行二次约简,以筛选关键初态特征Cj(j=1, 2,…, q)。
(1)基于粗糙集理论一次约简初态特征。首先分别建立基于燃弧能量、接触压降的粗糙集信息系统。选择离散化方法,对两个信息系统中的条件属性值和决策属性值离散化形成各自的决策表。条件属性离散化实现了初态特征等级的划分。决策属性离散化实现了交流接触器电寿命等级Gi(i=1, 2,…, p)的划分。在建立决策表之后,选择属性约简方法对两个决策表分别进行属性约简,得到燃弧能量与接触电阻各自的最简属性集。若最简属性集不唯一,计算不同寿命等级下属性离散值均值与理想值差的绝对值,进行累加以筛选初态特征的最佳属性集。
(2)基于粗糙集理论二次约简最佳属性集组合。将以上得到的两类初态特征的最佳属性集组合与决策属性构成二次决策表进行约简,获得燃弧能量与接触压降的综合最简属性集,以得到所筛选的关键初态特征。如上,若综合最简属性集不唯一,则选择包含两类初态特征的属性集,再根据累加绝对值筛选关键初态特征。
首先应结合建模样本进行预测方法的关键环节参数的确定,包括建立关键初态特征权重集,以及建立验证样本关键初态特征的匹配度表。之后利用二者构建独立证据,运用证据理论进行证据融合,获取类概率函数值决策验证样本个体预期电寿命 等级。
3.2.1 预测方法关键环节的确定
关键初态特征权重wj表示由初态特征Cj所构建的独立证据在决策预期电寿命等级中的重要程度,合理的权重分配是准确决策寿命等级的基础。主客观综合赋权法可以减少权重分配过程中信息的损失,使得赋权结果较为合理,因而采用主客观综合赋权法进行关键初态特征权重分配。
分析建模样本特征数据以主观赋权法建立主观权重集Ws;根据建模样本寿命及特征数据以客观赋权法建立客观权重集Wo;之后线性综合获取关键初态特征权重集W={w1, w2,…, wj}。
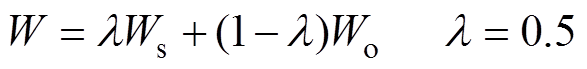 (13)
(13)在建立关键初态特征权重集后,还需获得验证样本关键初态特征的匹配度表,为证据理论中独立证据的构建做好准备。基于朴素贝叶斯分类模型中的属性条件密度P(Xj|Yi)建立交流接触器关键初态特征在不同寿命等级对应特征分布中的匹配度,具体过程如下。
针对建模样本,对应Gi寿命等级下的样本数量为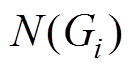 ,由
,由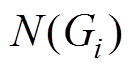 根据式(8)计算
根据式(8)计算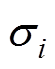 。
。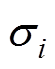 与
与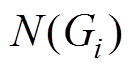 个Cj特征值作为高斯核函数的参数,
个Cj特征值作为高斯核函数的参数,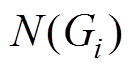 个高斯核函数线性叠加模拟了Gi寿命等级下Cj特征分布的情况。将验证样本关键初态特征Cj数值代入式(5),计算P(Cj|Gi)作为关键初态特征Cj对应于寿命等级Gi的匹配度
个高斯核函数线性叠加模拟了Gi寿命等级下Cj特征分布的情况。将验证样本关键初态特征Cj数值代入式(5),计算P(Cj|Gi)作为关键初态特征Cj对应于寿命等级Gi的匹配度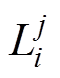 ,每个验证样本共获得p×q个匹配度,并根据式(14)对某一特征下的匹配度
,每个验证样本共获得p×q个匹配度,并根据式(14)对某一特征下的匹配度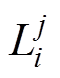 进行归一化处理。
进行归一化处理。
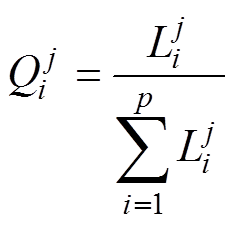 (14)
(14)3.2.2 基于证据理论的预期电寿命预测
在确定以上预测方法关键环节参数后,进行验证样本预期电寿命等级的不确定性推理。首先由划分的寿命等级Gi建立证据理论中的辨别框架为 = {G1, G2,…, Gp},再根据关键初态特征Cj的权重wj与验证样本匹配度Q建立独立证据,其对应的基本概率分配函数为mj。
= {G1, G2,…, Gp},再根据关键初态特征Cj的权重wj与验证样本匹配度Q建立独立证据,其对应的基本概率分配函数为mj。
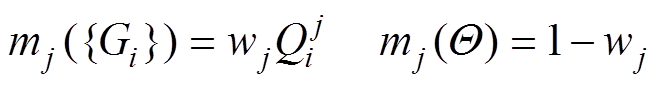 (15)
(15)在建立独立证据后,根据Dempster组合规则计算融合证据M。由M得到命题“交流接触器预期电寿命等级为Gi”的信任函数Bel(Gi)和似然函数Pl(Gi)分别为
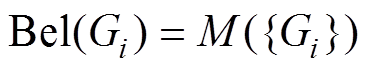 (16)
(16)
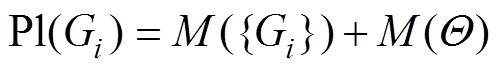 (17)
(17) 之后根据式(12)计算命题的类概率函数值F(Gi)。类概率函数值F(Gi)是命题“交流接触器预期电寿命等级为Gi”成立的不确定性度量。F(Gi)越大,命题的估计信任度越高。因此,决策原则为类概率函数值最大值F(Gi)max所对应寿命等级是验证样本个体预期电寿命等级。基于上述内容,本文所提出的交流接触器预期电寿命预测方法的具体流程如图2所示。
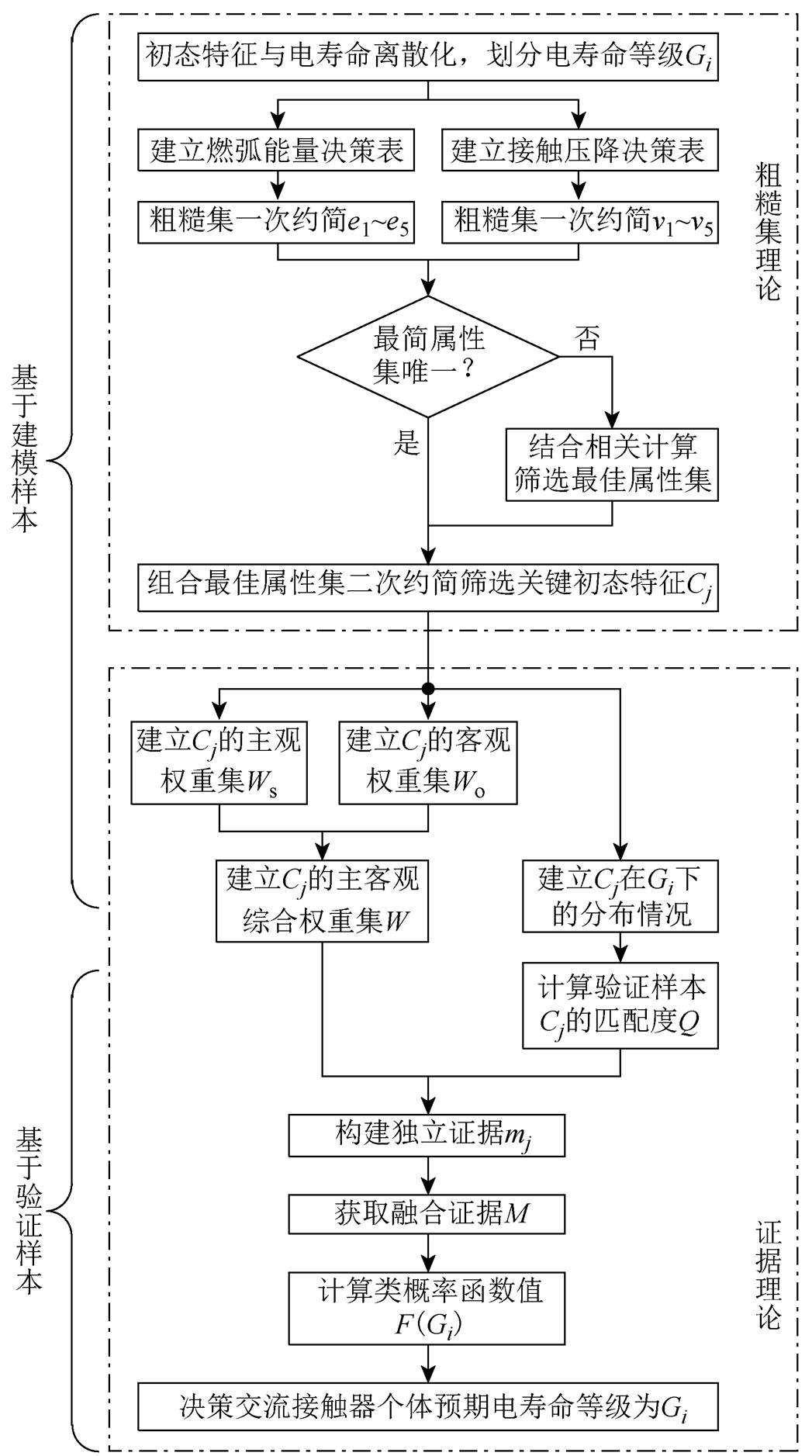
图2 交流接触器预期电寿命预测流程
Fig.2 Flow chart of AC contactor expected electrical life prediction
从11组试品的数据中,选用其中的9组x2~x4、x6~x11用于预测方法中关键环节的确定,剩下的两组x1、x5用来验证预测方法的有效性。由表5、表6去掉验证样本x1、x5的数据,建立两类初态特征的信息系统。
4.1.1 建立决策表
两类初态特征与寿命信息构成了粗糙集理论中的两个信息系统,要分别对两类初态特征进行约简,首先要以决策表的形式来表示信息系统,而决策表中的值要求采用离散数据,因此对条件属性Ce={e1, e2,…, e5}、Cv={v1, v2,…, v5}和决策属性D={接触器电寿命}进行离散化处理,分别建立燃弧能量决策表和接触压降决策表。条件属性根据数据特点采用经验法进行离散,决策属性则根据条件属性的分布情况进行离散。本实例中将条件属性与决策属性离散化划分为三个级别,也可以认为是三个模糊语言值,例如“小、中、大”,具体离散方法如下:e1~e5为五段燃弧能量均值,采用统一标准进行离散化,“1、2、3”分别表示其值属于[0, 11J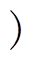 、[11J, 20J
、[11J, 20J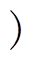 、[20J, +∞
、[20J, +∞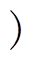 区间;v1~v5为五段接触压降均值,同理采用统一标准进行离散化,“1、2、3”分别表示其值属于[0, 2.6V
区间;v1~v5为五段接触压降均值,同理采用统一标准进行离散化,“1、2、3”分别表示其值属于[0, 2.6V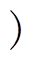 、[2.6V, 3.6V
、[2.6V, 3.6V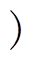 、[3.6V, +∞
、[3.6V, +∞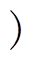 区间;对于接触器电寿命,“1、2、3”分别表示其值属于[0, 2
区间;对于接触器电寿命,“1、2、3”分别表示其值属于[0, 2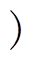 万次、[2, 5
万次、[2, 5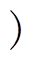 万次、[5, +∞
万次、[5, +∞ 万次区间,分别对应寿命等级“G1、G2、G3”。
万次区间,分别对应寿命等级“G1、G2、G3”。
之后,按照上述离散规则,对相应的初态特征与寿命信息进行离散操作,燃弧能量、接触压降的决策表见表8和表9。
表8 燃弧能量决策表
Tab.8 Arcing energy decision table
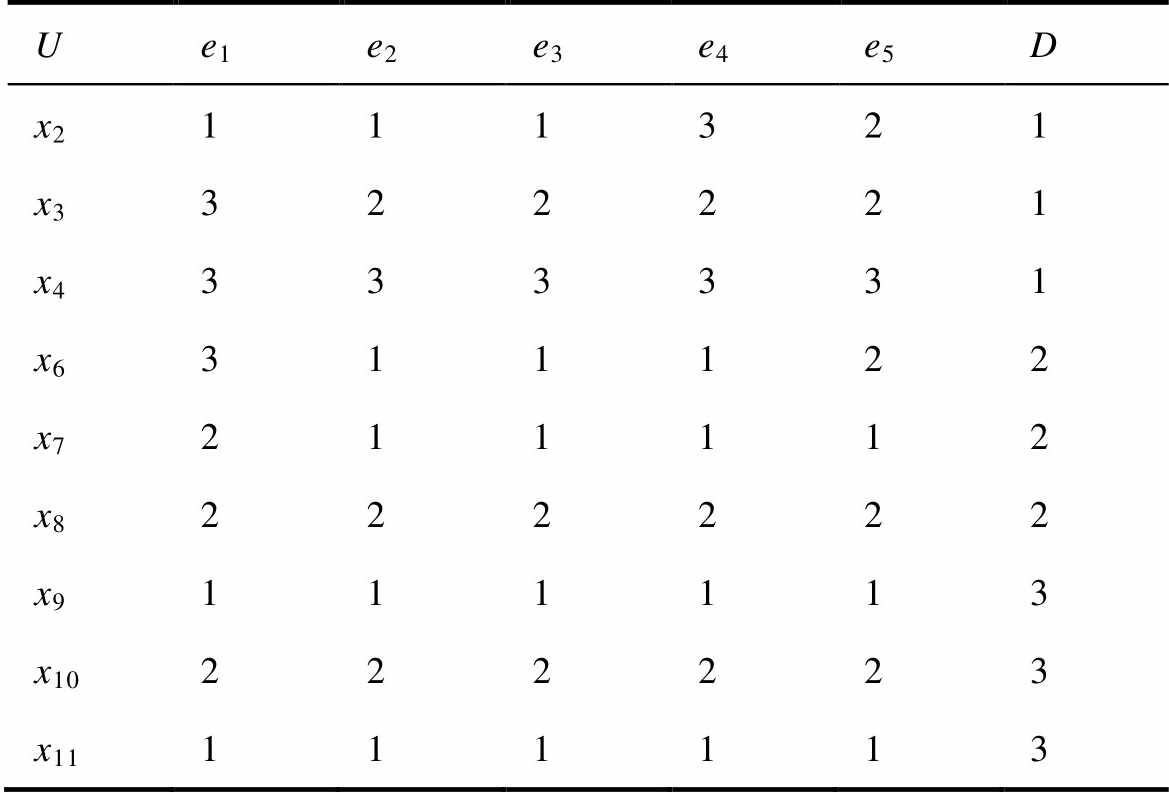
Ue1e2e3e4e5D x2111321 x3322221 x4333331 x6311122 x7211112 x8222222 x9111113 x10222223 x11111113
表9 接触压降决策表
Tab.9 Contact pressure drop decision table
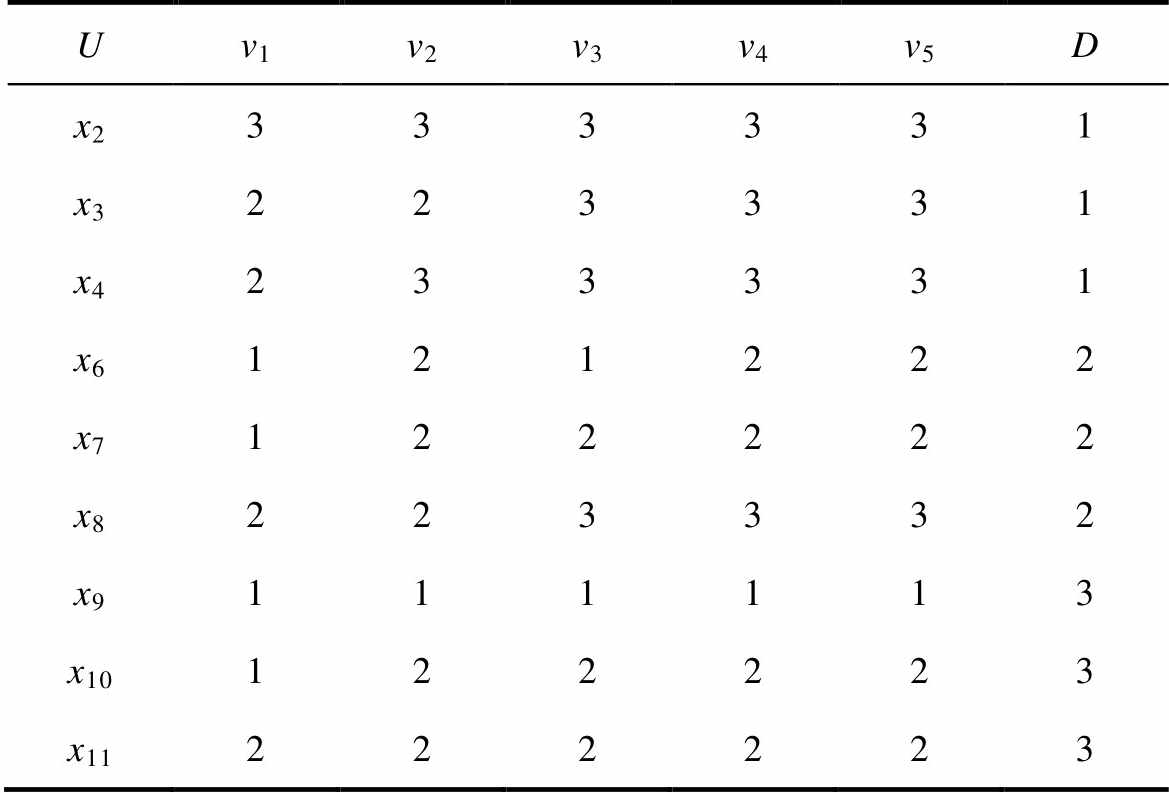
Uv1v2v3v4v5D x2333331 x3223331 x4233331 x6121222 x7122222 x8223332 x9111113 x10122223 x11222223
4.1.2 粗糙集一次约简结果分析
采用基于属性依赖度的约简算法对两个决策表分别进行约简。算法约简过程为将5个条件属性指标赋给0、1两种状态,0代表属性组合中没有该属性,1代表属性组合中有该属性,计算条件属性组合[0 0 0 0 1]~[1 1 1 1 1]的依赖度target1,并计算属性组合中0的个数所占的比重target2,获取目标函数target=target1+target2。目标函数值越大代表对应属性组合中属性越少,依赖度越高,目标函数值最大的属性组合即为最简属性集。经一次约简后,燃弧能量的最简属性集为{e1, e4},接触压降的最简属性集为{v1, v2, v3}。燃弧能量、接触压降最简属性集唯一,即为燃弧能量、接触压降最佳属性集,组合后进行二次约简。
4.1.3 粗糙集二次约简结果分析
将燃弧时间、接触压降的最佳属性集组合与决策属性构成二次决策表,采用基于属性依赖度的约简算法进行二次约简,综合最简属性集为{e1, e4, v1}、{e1, e4, v3}。综合最简属性集不唯一,通过v1、v3对应的累加绝对值筛选最终的关键初态特征。
在理想情况下“G1、G2、G3”寿命等级试品对应的属性离散值为“3、2、1”。计算表9中不同寿命等级下属性离散值均值与理想值差的绝对值进行累加,累加绝对值H越小,代表该属性与理想情况更为接近,v1、v3对应的累加绝对值见表10。
表10 接触压降分段均值对应的累加绝对值
Tab.10 Cumulatived absolute value corresponding to contact pressure drop sectional mean

v1v3 G12/30 G22/30 G31/32/3 H5/32/3
由表10可知,v3对应的累加绝对值较小,更贴近理想情况,因此最终选取e1、e4、v3为关键初态特征C1、C2、C3。
4.2.1 特征权重集与匹配度表的建立
G1法赋权过程无需构造判断矩阵及计算一致性检验,简便直观,灰关联定权通过计算评价因素与评价目标的关联度,确定评价因素的客观权重,因此采用G1-灰关联定权法获取关键初态特征权重集W,为证据理论中独立证据的构建做好准备。
首先由表5和表6可知,整体上建模样本燃弧能量对电寿命的区分程度比接触压降的高,主观上给出关键初态特征的相对重要程度C1=C2,C2= 1.2C3,根据G1法[24]建立主观权重集Ws;之后由表5和表6分析建模样本的寿命及特征数据,以建模样本的电寿命作为灰关联定权母序列,建模样本的关键初态特征作为灰关联定权子序列,对其进行预处理,分辨率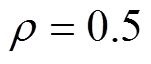 ,采用灰关联定权法[25]建立客观权重集Wo,最终根据式(13)线性组合客观权重集Wo和主观权重集Ws得到关键初态特征权重集W,见表11。
,采用灰关联定权法[25]建立客观权重集Wo,最终根据式(13)线性组合客观权重集Wo和主观权重集Ws得到关键初态特征权重集W,见表11。
表11 关键初态特征权重集
Tab.11 Weight set of key initial state characteristics
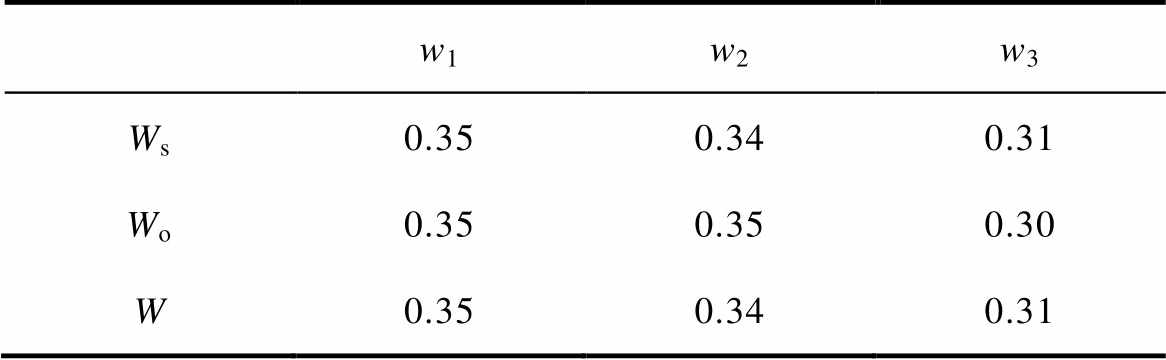
w1w2w3 Ws0.350.340.31 Wo0.350.350.30 W0.350.340.31
在建立关键初态特征权重集后,获取验证样本关键初态特征的匹配度表。根据表8获取Gi寿命等级下样本数量为N(Gi)并计算si,由表5和表6获取Gi寿命等级下建模样本的Cj特征值,二者作为N(Gi)个高斯核函数的参数,对高斯核函数线性叠加模拟Gi寿命等级下Cj特征分布的情况。将表5、表6中验证样本x1、x5关键初态特征值代入式(5),计算验证样本关键初态特征匹配度Q,见表12。
表12 验证样本关键初态特征匹配度
Tab.12 Matching degree of key initial characteristics for verification sample

j=1j=2j=3 x1110.51 000.26 000.23 x5000.11 10.840.46 00.160.43
4.2.2 验证样本预期电寿命测试
在建立关键初态特征权重集与验证样本关键初态特征匹配度表后,对验证样本预期电寿命等级进行不确定性推理。首先由划分的寿命等级Gi建立辨别框架为 ={G1, G2, G3},再根据式(15)构建独立证据对应的基本概率分配函数,见表13。
={G1, G2, G3},再根据式(15)构建独立证据对应的基本概率分配函数,见表13。
表13 基本概率分配函数
Tab.13 Basic probability assignment

mj({G1})mj({G2})mj({G3}) x1m10.35000.65 m20.34000.66 m30.160.080.070.69 x5m100.3500.65 m200.290.050.66 m30.030.140.130.69
基于Dempster 组合规则进行证据组合,获取融合证据M,见表14。
表14 融合证据
Tab.14 Fusion evidence

M({G1})M({G2})M({G3}) Mx10.600.050.030.32 Mx50.020.550.100.33
根据式(16)、式(17)由M建立框架 上的信任函数Bel(Gi)与似然函数Pl(Gi),再根据式(12)计算验证样本预期电寿命隶属于Gi寿命等级的类概率函数值,见表15。
上的信任函数Bel(Gi)与似然函数Pl(Gi),再根据式(12)计算验证样本预期电寿命隶属于Gi寿命等级的类概率函数值,见表15。
表15 类概率函数
Tab.15 Genus probability function
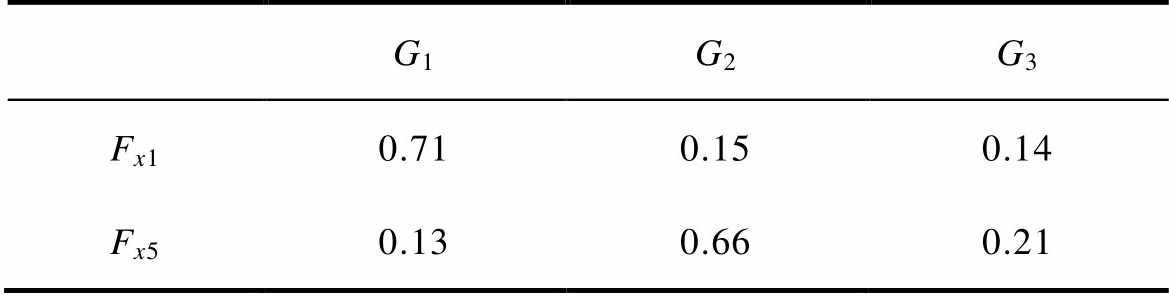
G1G2G3 Fx10.710.150.14 Fx50.130.660.21
基于类概率函数表和决策原则,验证样本电寿命等级预测结果与实际结果,见表16。
表16 预期电寿命与实际电寿命
Tab.16 Expected electrical life and actual electrical life
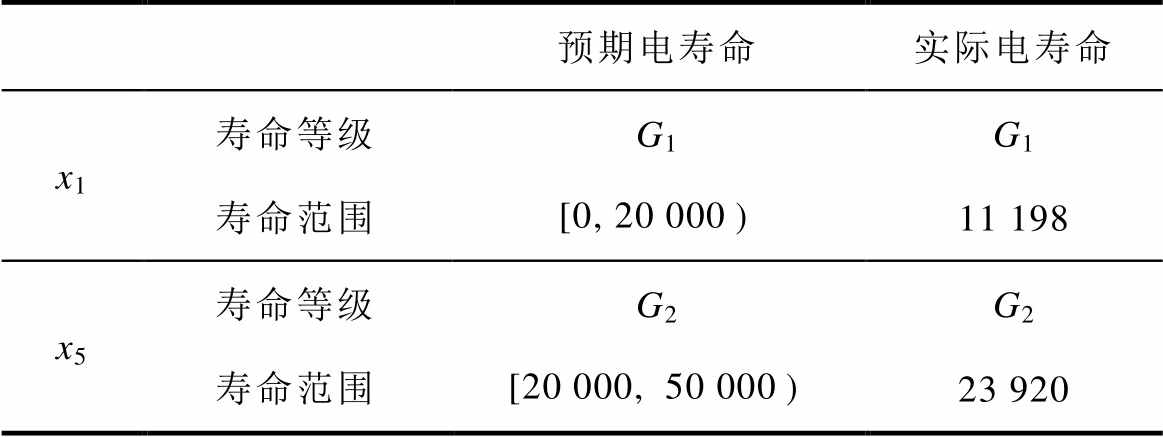
预期电寿命实际电寿命 x1寿命等级G1G1 寿命范围[0, 20 00011 198 x5寿命等级G2G2 寿命范围[20 000,50 00023 920
根据以上方法,接触器x1预期电寿命等级为G1,接触器x5预期电寿命等级为G2,均与实际结果一致。
之后,在其他条件不变的情况下,改变建模-验证的样本比例进行预期电寿命预测,全部预测结果见表17。
表17 不同样本比例下的预测结果
Tab.17 Prediction results at different sample ratios

建模-验证的样本比例正确预测错误预测 9-2x1、x5无 8-3x1、x5、x11无 7-4x1、x5、x7、x11无 6-5x1、x5、x7、x11x2
由表17可知,在6个样本建模、5个样本测试的情况下,接触器x2没有正确预测其电寿命等级,在其他情况下,均对相应的验证样本预测出了正确的电寿命等级,体现了该方法在小子样的情况下,具有一定的实用性和较强的灵活性,但建模样本过少会导致个别样本预测错误,因此仍需保证一定数量的样本建模,以使粗糙集约简结果及概率密度函数的构建更为合理。因此为了更好地说明整体方法的实施过程,上文以9个样本建模,2个样本测试进行说明。
基于交流接触器个体初期的性态变化与电寿命的关系,本文提出一种基于粗糙集与证据理论的交流接触器预期电寿命预测方法。该方法针对小子样、贫信息进行不确定性推理,实现交流接触器个体预期电寿命的定性预测。本文研究成果如下:
1)针对研究试品,由斯皮尔曼等级相关系数并结合特征参量与电寿命的总体变化趋势,发现寿命初期燃弧时间、燃弧能量、接触电阻、接触压降与电寿命存在负相关关系,它们的差异在一定程度上可以反映交流接触器个体电寿命的长短。
2)基于粗糙集理论从燃弧能量、接触压降的分段均值中筛选关键初态特征,预测所需数据量较小,减少了预测方法运算的复杂度。采用证据理论对多个证据融合,综合考虑了多个关键初态特征对寿命等级预测的影响,更好地区分了特征信息在寿命等级上的差异。粗糙集与证据理论联合应用充分发挥了相关方法的优点,使得两种方法在一定程度上进行互补。
3)在小子样且保证一定数量样本建模的情况下,针对不同的建模-验证的样本比例进行预期电寿命预测,达到了较好的预测效果,具有一定的实用性和较强的灵活性。
该方法仍可进一步研究改进,完善初态信息后进一步实现交流接触器电寿命的定量预测,以及研究交流接触器实际工况条件对电寿命的影响与预测模型参数的修正,亦可推广应用于其他低压开关电器产品的预期电寿命预测中,提高方法的适用性。
参考文献
[1] 李奎, 李晓倍, 郑淑梅, 等. 基于BP神经网络的交流接触器剩余电寿命预测[J]. 电工技术学报, 2017, 32(15): 120-127.
Li Kui, Li Xiaobei, Zheng Shumei, et al. Residual electrical life prediction for AC contactor based on BP neural network[J]. Transactions of China Electro- technical Society, 2017, 32(15): 120-127.
[2] 李奎, 段宇, 黄少坡, 等. 基于Wiener过程的交流接触器剩余电寿命预测[J]. 中国电机工程学报, 2018, 38(13): 3978-3986, 4039.
Li Kui, Duan Yu, Huang Shaopo, et al. Residual electrical life prediction of AC contactor based on the wiener process[J]. Proceedings of the CSEE, 2018, 38(13): 3978-3986, 4039.
[3] 李志刚, 刘伯颖, 李玲玲, 等. 基于小波包变换及RBF神经网络的继电器寿命预测[J]. 电工技术学报, 2015, 30(14): 233-240.
Li Zhigang, Liu Boying, Li Lingling, et al. Life prediction of relay based on wavelet packet transform and RBF neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 233-240.
[4] 刘建强, 陈爱峰, 闫一凡, 等. 高速列车电磁接触器可靠性评估方法[J]. 电工技术学报, 2018, 33(增刊2): 461-471.
Liu Jianqiang, Chen Aifeng, Yan Yifan, et al. Reliability evaluation method of electromagnetic contactor used in high-speed train[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 461- 471.
[5] Zheng Shumei, Niu Feng, Li Kui, et al. Analysis of electrical life distribution characteristics of AC contactor based on performance degradation[J]. IEEE Transactions on Components Packaging and Manufa- cturing Technology, 2018, 8(9): 1604-1613.
[6] 李华, 孙东旺, 贺鹏举, 等. 基于超程时间回归模型的继电器寿命预测方法[J]. 电工技术学报, 2013, 28(增刊2): 414-417, 423.
Li Hua, Sun Dongwang, He Pengju, et al. The method of relay life prediction based on the regression model of super-path time[J]. Transactions of China Electro- technical Society, 2013, 28(S2): 414-417, 423.
[7] 孙永奎, 张玉琢, 徐超凡, 等. 安全型继电器失效机理判别与寿命预测[J]. 交通运输工程学报, 2018, 18(3): 138-147.
Sun Yongkui, Zhang Yuzhuo, Xu Chaofan, et al. Failure mechanisms discrimination and life predi- ction of safety relay[J]. Journal of Traffic and Transportation Engineering, 2018, 18(3): 138-147.
[8] Cui Xinglei, Zhou Xue, Zhai Guofu, et al. Electrical lifespan prediction of HVDC relay based on the accumulated arc erosion mass[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2018, 8(3): 356-363.
[9] 李志刚, 张菲菲, 李玲玲. 基于元器件初始信息的寿命评估方法[J]. 机械工程学报, 2014, 50(16): 41-46.
Li Zhigang, Zhang Feifei, Li Lingling. Lifetime evaluation approach based on initial information of components[J]. Journal of Mechanical Engineering, 2014, 50(16): 41-46.
[10] 李玲玲, 张士暖, 李志刚, 等. 基于粗糙集理论和生命初态信息的继电器寿命预测方法[J]. 电工技术学报, 2016, 31(18): 46-53.
Li Lingling, Zhang Shinuan, Li Zhigang, et al. The life prediction method of relay based on rough set theory and relay’s initial life information[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 46-53.
[11] 林晓宁, 蔡金锭. 基于粗糙集理论的变压器油纸绝缘状态评估[J]. 电力系统保护与控制, 2019, 47(7): 22-29.
Lin Xiaoning, Cai Jinding. Evaluation of transformer oil-paper insulation based on rough set theory[J]. Power System Protection and Control, 2019, 47(7): 22-29.
[12] Peng Xiaosheng, Wen Jinyu, Li Zhaohui, et al. Rough set theory applied to pattern recognition of partial discharge in noise affected cable data[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 147-156.
[13] Fetouh T, Zaky M. New approach to design svc-based stabilizer using genetic algorithm and rough set theory[J]. IET Generation, Transmission & Distri- bution, 2017, 11(2): 372-382.
[14] 刘征宇, 王雪松, 汤伟, 等. 基于可信度因子推理模型的电池组均衡方法[J]. 中国机械工程, 2019, 30(9): 1090-1096.
Liu Zhengyu, Wang Xuesong, Tang Wei, et al. A battery equalization strategy based on reasoning model of C-F[J]. China Mechanical Engineering, 2019, 30(9): 1090-1096.
[15] Li Shaoyi, Zhang Kai, Yin Jianfei, et al. A study on IR target recognition approach in aerial jamming environment based on bayesian probabilistic model[J]. IEEE Access, 2018, 7: 50300-50316.
[16] Barros D M O A, Luiz M R, Ribeiro E R. Short-circuit fault diagnosis based on the rough sets theory for a single-phase inverter[J]. IEEE Transa- ctions on Power Electronics, 2018, 34(5): 4747- 4764.
[17] Du Wei, ZhangChuan, Fang Ning, et al. A quantita- tive analysis of electromagnetic simulation model credibility[J]. IEEE Antennas and Wireless Pro- pagation Letters, 2019, 18(1): 34-38.
[18] 刘满君, 程林, 黄道姗, 等. 基于运行可靠性理论的高可靠性供电路径搜索方法[J]. 电工技术学报, 2019, 34(14): 3004-3011.
Liu Manjun, Cheng Lin, Huang Daoshan, et al. The high reliability supply path searching method based on the operational reliability theory[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3004-3011.
[19] 耿俊豹, 邱玮, 孔祥纯, 等. 基于粗糙集和D-S证据理论的设备技术状态评估[J]. 系统工程与电子技术, 2008, 30(1): 112-115.
Geng Junbao, Qiu Wei, Kong Xiangchun, et al. Technical condition evaluation for devices based on rough set theory and D-S evidence theory[J]. Systems Engineering and Electronics, 2008, 30(1): 112-115.
[20] 孙伟超, 李文海, 李文峰. 融合粗糙集与D-S证据理论的航空装备故障诊断[J]. 北京航空航天大学学报, 2015, 41(10): 1902-1909.
Sun Weichao, Li Wenhai, Li Wenfeng. Avionic devices fault diagnosis based on fusion method of rough set and D-S theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1902-1909.
[21] Deval S M, Shoushun C, Soon L K. A Hamming distance and spearman-correlation based star identi- fication algorithm[J]. IEEE Transactions on Aero- space and Electronic Systems, 2018, 55(1): 17-30.
[22] 江帆, 杨洪耕. 基于选择性贝叶斯分类的非侵入式负荷识别方法[J]. 电力建设, 2019, 40(2): 94-99.
Jiang Fan, Yang Honggeng. Non-intrusive load identification method based on selected Bayes classifier[J]. Electric Power Construction, 2019, 40(2): 94-99.
[23] 刘建强, 刘传铎, 王轶欧, 等. 单相PWM整流器IGBT及直流侧电容故障诊断方法[J]. 电工技术学报, 2019, 34(增刊1): 244-257.
Liu Jianqiang, Liu Chuanduo, Wang Yiou, et al. Fault diagnosis method for IGBT and DC-link capacitor of single-phase PWM rectifier[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 244-257.
[24] 鲍学英, 柴乃杰, 王起才. 基于G1法和改进DEA的铁路绿色施工节能措施综合效果研究[J]. 铁道学报, 2018, 40(10): 15-22.
Bao Xueying, Chai Naijie, Wang Qicai. Com- prehensive effect of energy-saving measures on railway green construction based on G1 method and improved DEA models[J]. Journal of the China Railway Society, 2018, 40(10): 15-22.
[25] 储冉, 王怀秀, 王亚慧. 基于熵权与灰关联度定权的VIKOR多准则综合评价研究[J]. 现代电子技术, 2018, 41(24): 162-166, 169.
Chu Ran, Wang Huaixiu, Wang Yahui. Research on multi-criteria comprehensive evaluation based on entropy weight and grey relational legal weight for VIKOR[J]. Modern Electronics Technique, 2018, 41(24): 162-166, 169.
Expected Electrical Life Prediction of AC Contactor Based on Rough Set and Evidence Theory
Abstract At present, the research on the electrical life prediction of low-voltage electrical apparatus mostly focuses on the residual electrical life prediction. However, predicting the expected electrical life is more effective in guiding the use and maintenance of products and improving the reliability of the system during service period. AC contactor's initial state characteristics can reflect the length of the individual's electrical life to a certain extent, so a method for predicting the expected electrical life of AC contactor based on rough set and evidence theory was proposed. Firstly, the rough set theory and corresponding calculation were used to obtain the key initial state characteristics through twice screening. Secondly, the weight set of key initial state characteristics was established by subjective and objective comprehensive weighting method and the matching degree table of verification sample's key initial state characteristics was established based on the attribute condition density. Finally, the independent evidence was constructed by the matching degree table and weight set, then evidence theory was used to fuse evidences and decide the individual's expected electrical life grade of verification sample. The measured data proves that in the case of small samples, the method can qualitatively evaluate the expected electrical life of the AC contactor and the prediction effect is good.
keywords:AC contactor, rough set theory, attribute conditional density, evidence theory, life prediction
中图分类号:TM572.2
DOI: 10.19595/j.cnki.1000-6753.tces.190633
孙曙光 男,1979年生,博士,副教授,研究方向为智能检测与故障诊断。E-mail: sunshuguang_2000@163. com(通信作者)
王锐雄 男,1994年生,硕士研究生,研究方向为检测技术与自动化装置。E-mail: 1362052701@qq. com
收稿日期 2019-05-23
改稿日期 2019-09-20
河北省教育厅资助科研项目资助(ZD2016108)。
(编辑 郭丽军)