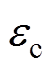 指的是实际位置点与参考轮廓的最短距离,轮廓误差示意图如图1所示。可以看出,轮廓误差是一个仅与实际位置和参考轮廓形状相关的几何概念。
指的是实际位置点与参考轮廓的最短距离,轮廓误差示意图如图1所示。可以看出,轮廓误差是一个仅与实际位置和参考轮廓形状相关的几何概念。摘要 针对直驱XY平台在加工高速度和尖角轮廓时精度较差的问题,提出一种在全局任务坐标系(GTCF)中采用迭代学习控制(ILC)和互补滑模控制(CSMC)相结合的轮廓控制方法。首先,利用实际轮廓误差的一阶导数构建轮廓误差模型,并将轮廓误差和轮廓运动轨迹作为控制变量建立GTCF,使系统能够协调运行。然后,采用ILC对轮廓跟踪过程中的未建模动态进行补偿,并利用CSMC抑制直驱XY平台伺服系统中参数变化、外部扰动等不确定性因素的影响。最后,系统实验结果表明,该控制方法具有较强的鲁棒性和快速的轮廓跟踪性,能够实现更精确的控制性能,减小系统的轮廓误差,进而改进直驱XY平台伺服系统的高精度轮廓加工性能。
关键词:直驱XY平台 全局任务坐标系 迭代学习控制 互补滑模控制 轮廓控制
为满足制造业的生产要求,永磁直线同步电动机(Permanent Magnet Linear Synchronous Motor, PMLSM)驱动的XY平台因其结构简单和响应速度快等优点被应用于精密加工设备等领域[1-2]。然而,由于两轴之间运动不协调和系统不确定性产生的轮廓误差,将严重限制直驱XY平台伺服系统的轮廓运动控制性能[3-4]。因此,应建立先进的协调机制以保证两轴协调控制,并设计强鲁棒性控制器,抑制系统不确定性因素的影响,从而减少轮廓误差,以满足直驱XY平台伺服系统的轮廓控制要求。
为实现优异的轮廓加工性能,文献[5]提出一种基于零极点对消的前馈控制方法,通过减小单轴的跟踪误差来提高系统的轮廓精度。但仅减小单轴的跟踪误差不能有效减小轮廓误差[6]。文献[7]提出了交叉耦合控制(Cross-Coupled Control, CCC),利用反馈实时计算出的轮廓误差,在各轴控制器中产生附加的补偿信号,以改善各轴的协调运动。文献[8]将一种局部近似的方法应用于位置环CCC。然而,CCC仅适用于斜率缓慢时变的线性轮廓,对于高速度大曲率或者存在尖角的轮廓,该方法产生的轮廓误差较大。文献[9]提出了一种局部任务坐标系(Local Task Coordinate Frame, LTCF),将系统的轮廓控制转化为轮廓误差镇定问题和轮廓快速跟踪问题。但是,与CCC类似,LTCF使用位置跟踪误差来估计轮廓误差,这种轮廓误差的计算方法不够精确。文献[10]采用迭代学习控制(Iterative Learning Control, ILC)补偿重复轮廓跟踪任务中的未建模动态,然而ILC易受到系统中不确定性因素的影响,所以必须设计控制器对不确定性进行控制。滑模控制具有响应快,对系统参数变化和外部扰动等不确定性具有强鲁棒性的优点,成为在非线性控制系统中广泛应用的方法[11]。
因此,在全局任务坐标系(GlobalTask Coor- dinate Frame, GTCF)中,采用ILC和互补滑模控制(Complementary Sliding Mode Control, CSMC)相结合的控制方法。GTCF将实际轮廓误差的一阶导数近似为轮廓误差,在加工高速度和大曲率轮廓时可以保证两轴间的协调控制。ILC通过迭代学习误差信号,将结果输入CSMC,对未建模动态进行补偿;CSMC用于抑制系统中不确定性因素,从而提高了轮廓精度。实验验证了所提出的控制方案能够实现优异的轮廓控制性能,满足直驱XY平台高精密加工要求。
直驱XY平台伺服系统的轮廓误差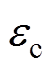 指的是实际位置点与参考轮廓的最短距离,轮廓误差示意图如图1所示。可以看出,轮廓误差是一个仅与实际位置和参考轮廓形状相关的几何概念。
指的是实际位置点与参考轮廓的最短距离,轮廓误差示意图如图1所示。可以看出,轮廓误差是一个仅与实际位置和参考轮廓形状相关的几何概念。
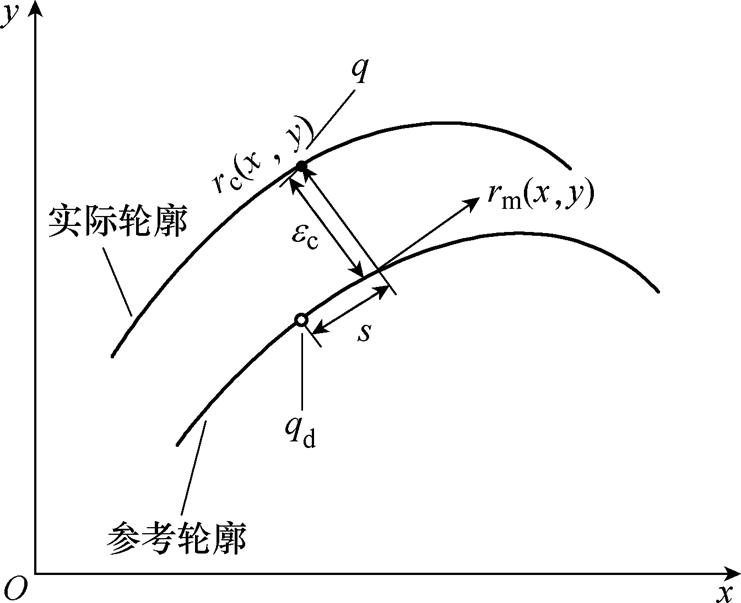
图1 轮廓误差示意图
Fig.1 Schematic of contouring error
首先,XY平台的参考轮廓表示为
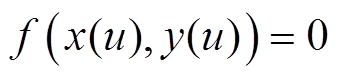 (1)
(1)式中,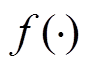 为一个已知的光滑曲线;u为时间t的参数。
为一个已知的光滑曲线;u为时间t的参数。
然后,定义GTCF为
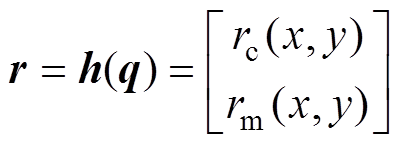 (2)
(2)式中,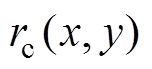 为实际轮廓误差
为实际轮廓误差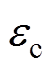 的一阶近似值,即
的一阶近似值,即
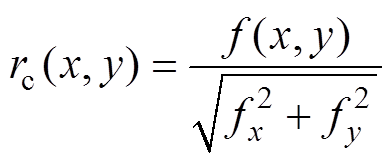 (3)
(3)
式中
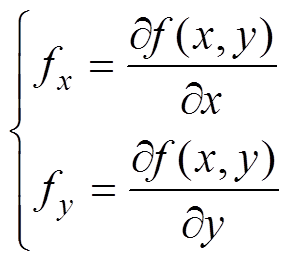 (4)
(4)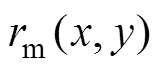 为参考点与实际位置沿参考轮廓的法线方向投影之间的距离,表示轮廓运动轨迹,即
为参考点与实际位置沿参考轮廓的法线方向投影之间的距离,表示轮廓运动轨迹,即
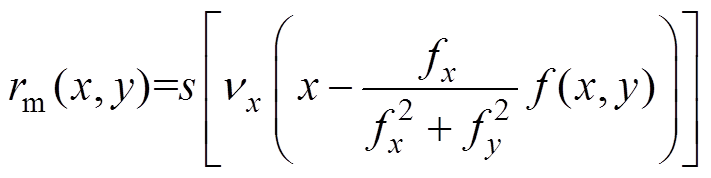 (5)
(5)
式中,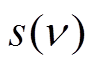 为轮廓曲线长度;
为轮廓曲线长度;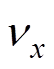 为
为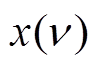 的反函数。
的反函数。
参考轮廓可表示为
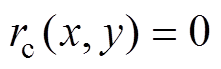 (6)
(6)对于参考轮廓上的点,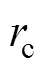 的方向与参考轮廓的法向一致。因此,可以用
的方向与参考轮廓的法向一致。因此,可以用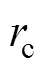 近似表示轮廓误差为
近似表示轮廓误差为
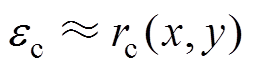 (7)
(7)
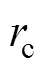 的方向矢量与沿参考轮廓法线方向的单位矢量相同,即
的方向矢量与沿参考轮廓法线方向的单位矢量相同,即
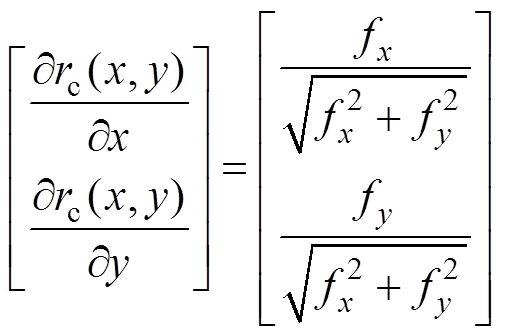 (8)
(8)
同时,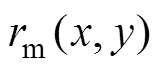 的方向矢量与沿参考轮廓的切线方向的单位矢量相同,即
的方向矢量与沿参考轮廓的切线方向的单位矢量相同,即
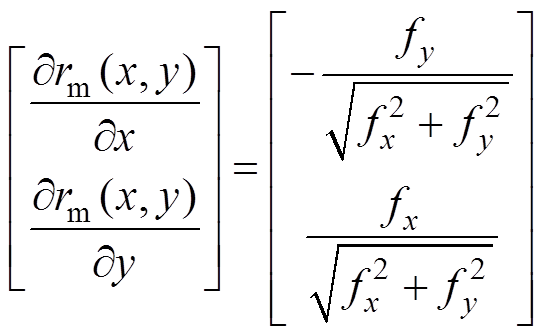 (9)
(9)所以,在GTCF中,轮廓控制的目标就转化为使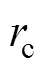 收敛为零并让
收敛为零并让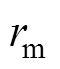 精确跟踪参考轮廓。
精确跟踪参考轮廓。
式(2)中坐标变换的雅可比矩阵可近似为
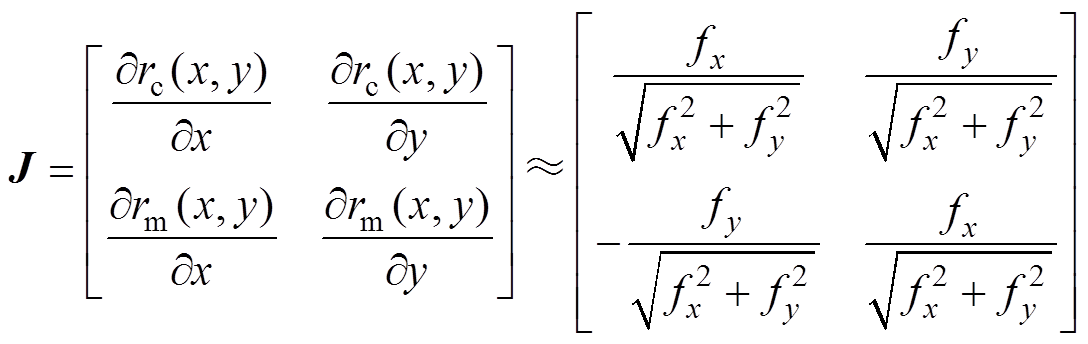 (10)
(10)式中,J为酉矩阵,即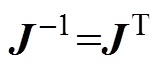 。因此,通过酉矩阵J建立了从笛卡尔坐标到GTCF的精确酉变换。
。因此,通过酉矩阵J建立了从笛卡尔坐标到GTCF的精确酉变换。
在笛卡尔坐标系中,直驱XY平台的动态方程为
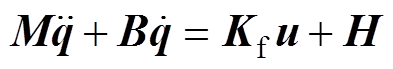 (11)
(11)式中,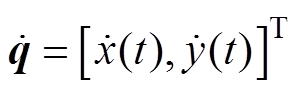 为速度矢量;
为速度矢量;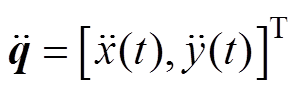 为加速度矢量;
为加速度矢量;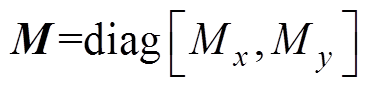 为动子总质量;B=
为动子总质量;B= 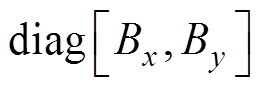 为黏滞摩擦因数;
为黏滞摩擦因数;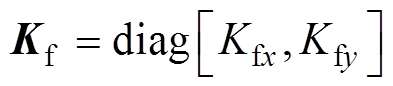 为电磁推力常数;u为控制输入矢量;H为包括系统参数变化、外部扰动和摩擦力等非线性扰动的总不确定性。
为电磁推力常数;u为控制输入矢量;H为包括系统参数变化、外部扰动和摩擦力等非线性扰动的总不确定性。
由式(2)和式(10)得
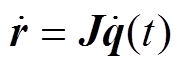 (12)
(12)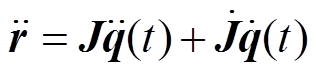 (13)
(13)
因此,将式(12)、式(13)代入式(11),并在等式两边同时乘以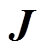 ,得
,得
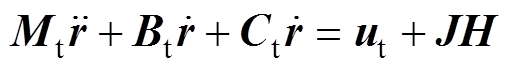 (14)
(14)式中
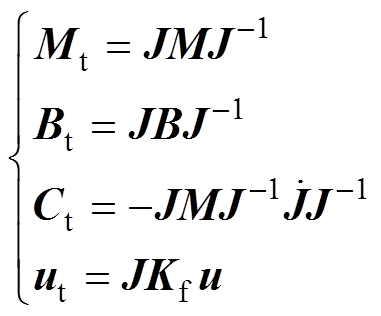 (15)
(15)
令
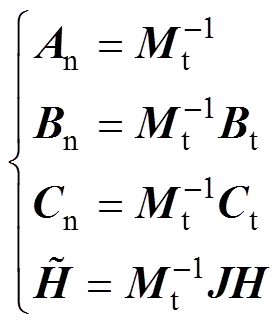 (16)
(16)将式(16)代入式(15),得到GTCF中的动态方程
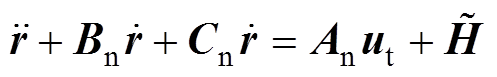 (17)
(17)
式中,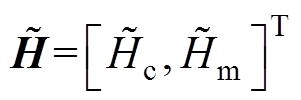 ;
;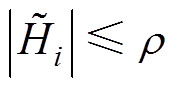 ,i代表c或m;r 为正常数。
,i代表c或m;r 为正常数。
基于GTCF-LCSMC的直驱XY平台伺服系统框图如图2所示,图2中主要包括GTCF、ILC和CSMC等环节。GTCF将保证双轴协调控制,以应对高速大曲率以及尖角的轮廓加工问题;ILC利用误差信号,采用前馈控制对参考轮廓进行修正,提高动态响应速度;CSMC补偿系统不确定性,增强系统的鲁棒性。
ILC可以在没有精确动态模型的情况下自动生成最佳控制信号,从而对轮廓实现跟踪,因此对于高精度运动控制具有重要意义[12]。ILC可用于优化轨迹,以补偿轮廓控制的未建模不确定性。
在GTCF中定义输出误差矢量为
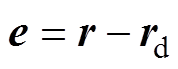 (18)
(18)式中,rd为参考轮廓。ILC的输出量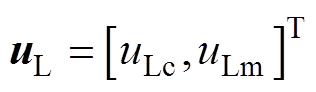 以前馈控制方式调整rd,从而生成修正轮廓
以前馈控制方式调整rd,从而生成修正轮廓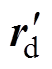 ,即
,即
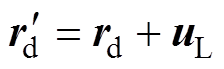 (19)
(19)
同时,修正误差向量为
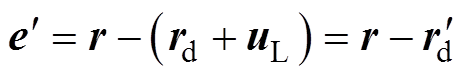 (20)
(20)XY平台伺服系统的动态方程与CSMC视为一个整体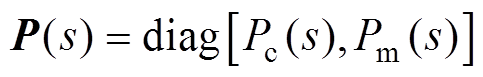 ,则系统动态方程表示为
,则系统动态方程表示为
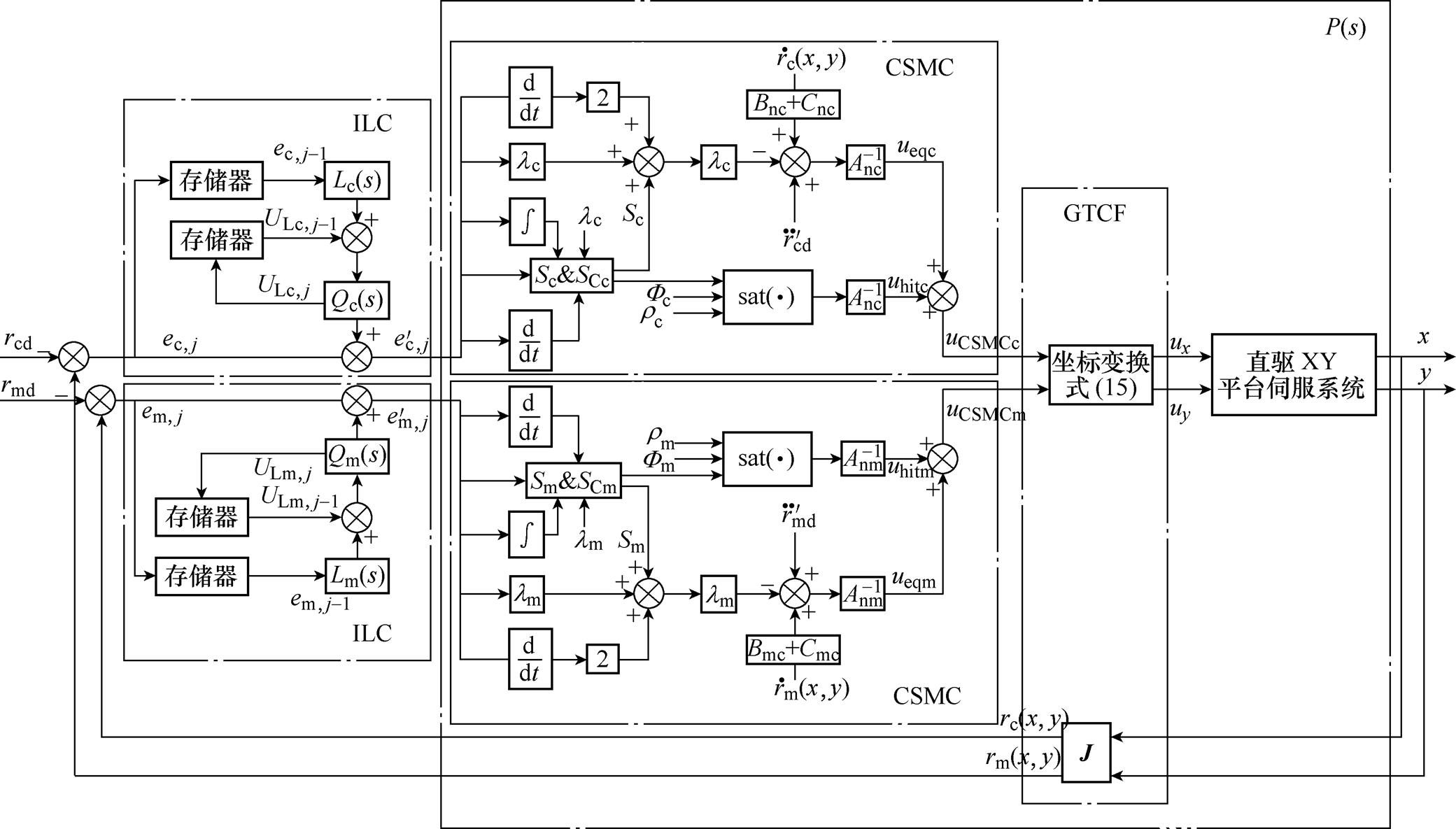
图2 基于GTCF-LCSMC的直驱XY平台伺服系统框图
Fig.2 Block diagram of direct drive XY table servo system based on GTCF-LCSMC
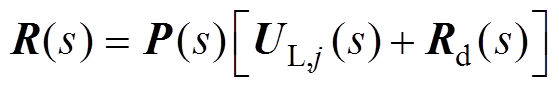 (21)
(21)式中,j为迭代次数;UL为迭代学习控制律。为产生最佳的控制输入,迭代学习控制律表示为
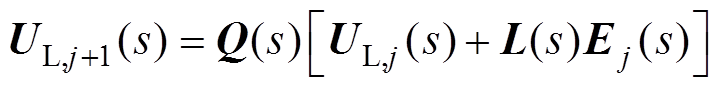 (22)
(22)
式中,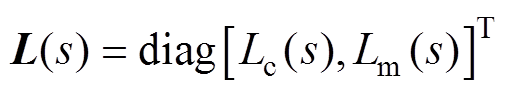 为学习函数矩阵;
为学习函数矩阵;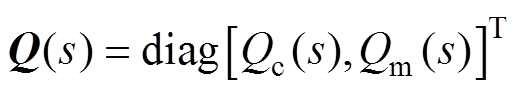 为Q滤波器。由于PD型学习函数具有结构简单和可调性高等优点,因此设计PD型学习函数为
为Q滤波器。由于PD型学习函数具有结构简单和可调性高等优点,因此设计PD型学习函数为
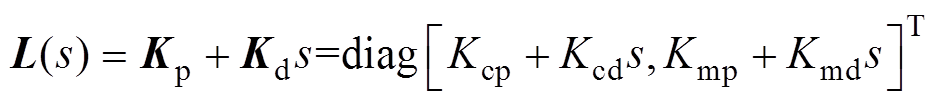 (23)
(23)ILC系统收敛的充要条件为
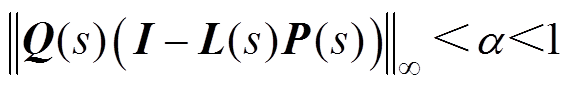 (24)
(24)
式中,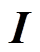 为单位矩阵;
为单位矩阵;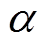 为收敛率。令
为收敛率。令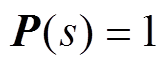 ,将式(23)代入式(24)得
,将式(23)代入式(24)得
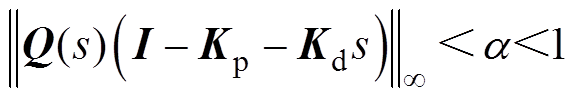 (25)
(25)令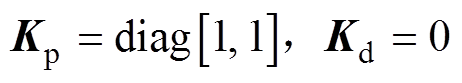 ,则收敛率
,则收敛率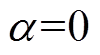 。此时ILC经过一次迭代后便可收敛,ILC的收敛性得到保证。
。此时ILC经过一次迭代后便可收敛,ILC的收敛性得到保证。
CSMC能够很好地补偿系统中摩擦力、参数变化等不确定性,采用两个滑模面相结合的设计,进一步提高系统的抗扰能力[13]。为了满足控制要求,设计广义滑模面S为
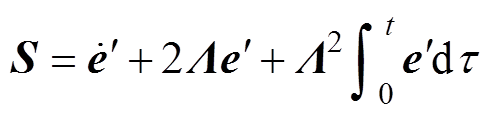 (26)
(26)式中,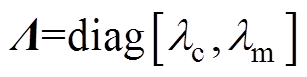 ,
,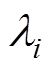 为正常数。对式(26)求导,并结合式(17)和式(20),得
为正常数。对式(26)求导,并结合式(17)和式(20),得
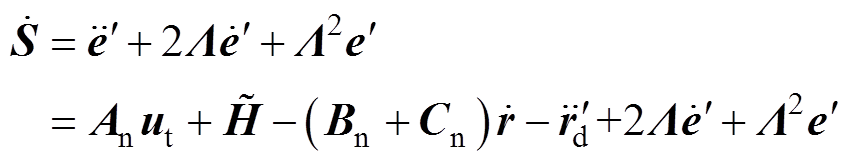 (27)
(27)
设计互补滑模面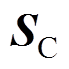 为
为
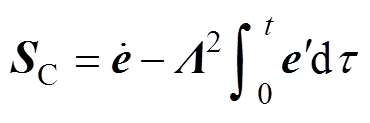 (28)
(28)在CSMC中,广义滑模面和互补滑模面的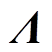 相同。因此
相同。因此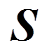 与
与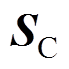 的关系为
的关系为
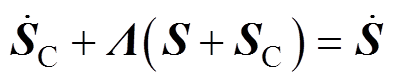 (29)
(29)
根据式(26)~式(28),得到CSMC的控制律![]() 为
为
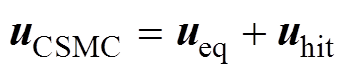 (30)
(30)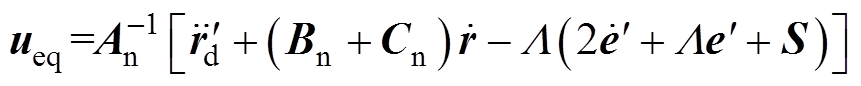 (31)
(31)
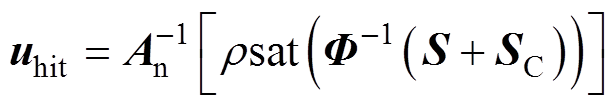 (32)
(32)
式中,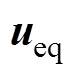 为等效控制律;
为等效控制律;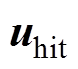 为切换控制律;
为切换控制律;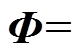
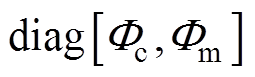 为边界层厚度。
为边界层厚度。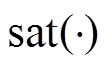 为饱和函数,表示为
为饱和函数,表示为
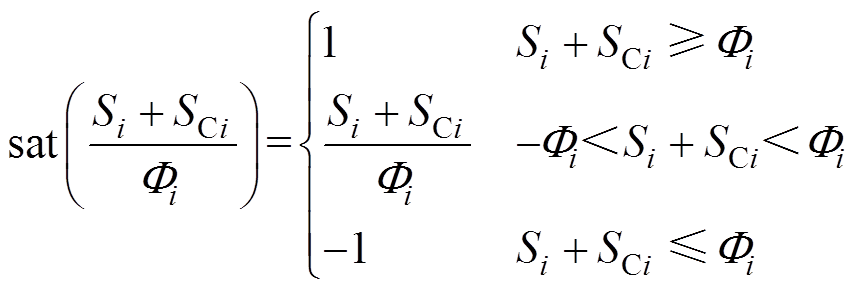 (33)
(33)定义李雅普诺夫函数为
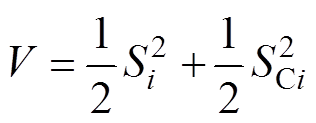 (34)
(34)
对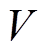 求导,并结合式(23)和式(29)~式(32),得
求导,并结合式(23)和式(29)~式(32),得
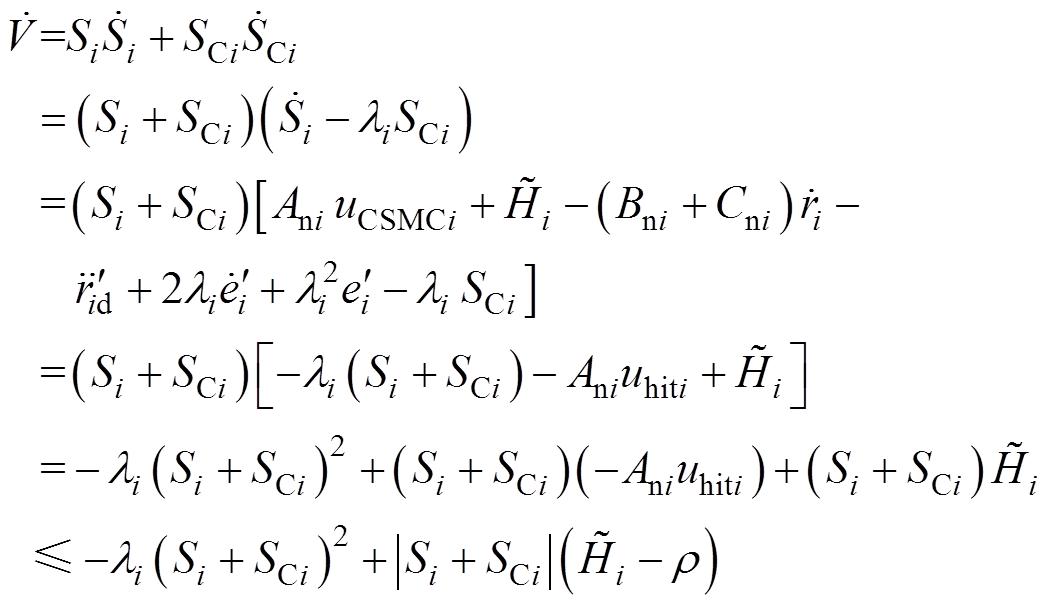 (35)
(35)由式(17)中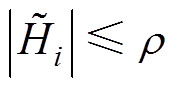 ,得
,得![]() 。这就保证了系统可以在有限时间内达到边界层,从而可以保证直驱XY平台伺服系统的稳定性。
。这就保证了系统可以在有限时间内达到边界层,从而可以保证直驱XY平台伺服系统的稳定性。
实验中选择慧摩森科技公司生产的LM22-26系列XY平台作为控制对象进行实验研究。采用美国GSI公司的Micro-EMercury II 1600-40型光栅编码器作为两轴位置传感器,X-RS232和Y-RS232分别为PC与X轴、Y轴的驱动器通信口。XY平台伺服系统硬件结构图如图3所示。
XY平台中PMLSM参数: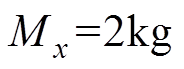 ,
,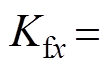
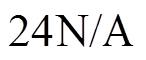 ,
,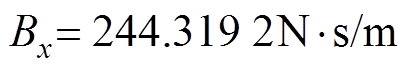 ;
;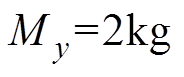 ,
,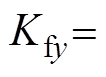
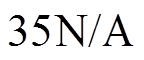 ,
,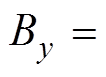
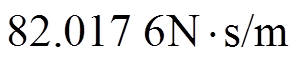 。通过不断调节参数使系统运行状态良好,采用CSMC的参数设置为r =3,lc=35,
。通过不断调节参数使系统运行状态良好,采用CSMC的参数设置为r =3,lc=35,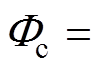
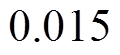 ,lm=12,
,lm=12,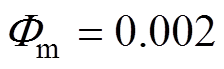 。系统分别采用LTCF- CSMC、GTCF-CSMC、GTCF-LCSMC三种控制方案进行实验。
。系统分别采用LTCF- CSMC、GTCF-CSMC、GTCF-LCSMC三种控制方案进行实验。
为验证直驱XY平台伺服系统的鲁棒性和轮廓跟踪性能,对系统输入xd(t)=0.02cos(pt),yd(t)= 0.02sin(pt)的圆形轮廓,并对两轴同时施加如图4a所示的外部扰动,系统产生的轮廓误差如图4b~图4d所示。对比实验结果可以发现,LTCF-CSMC、GTCF-CSMC和GTCF-LCSMC产生的轮廓误差的最大值分别为7.2mm、5.6mm和3.9mm。这表明在初始时刻LTCF由跟踪误差建立的轮廓误差模型不够精确,导致轮廓误差较大,而GTCF建立的轮廓误差模型,能对轮廓误差进行精确估计,从而显著提高系统的轮廓控制性能。GTCF-LCSMC的轮廓误差于0.12s趋近于零,表明ILC采用前馈控制对参考轮廓进行修正,响应速度更快。施加外部扰动后,LTCF-CSMC的轮廓误差变化范围为-2.7~3.7mm,GTCF-CSMC的轮廓误差变化范围为-1.8~2.6mm,GTCF-LCSMC的轮廓误差变化范围为-1.2~1.9mm。意味着GTCF-LCSMC能够抑制系统的不确定性,具有较强的鲁棒性。因此,GTCF-LCSMC不仅可以对轮廓误差进行精确估计,并且还具有优异的轮廓误差控制性能,能够降低系统的轮廓误差。
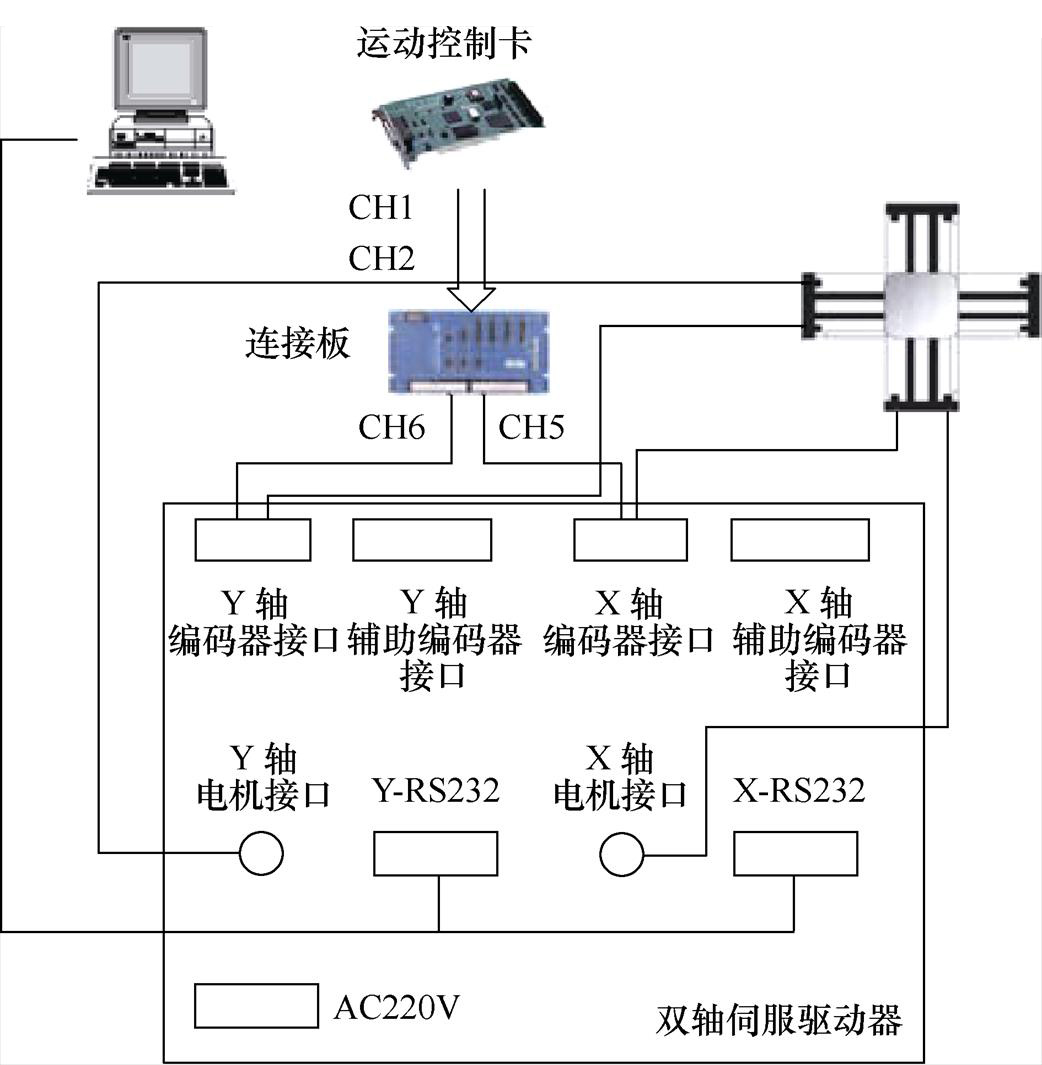
图3 XY平台伺服系统的硬件结构图
Fig.3 Hardware structure diagram of XY table servo system
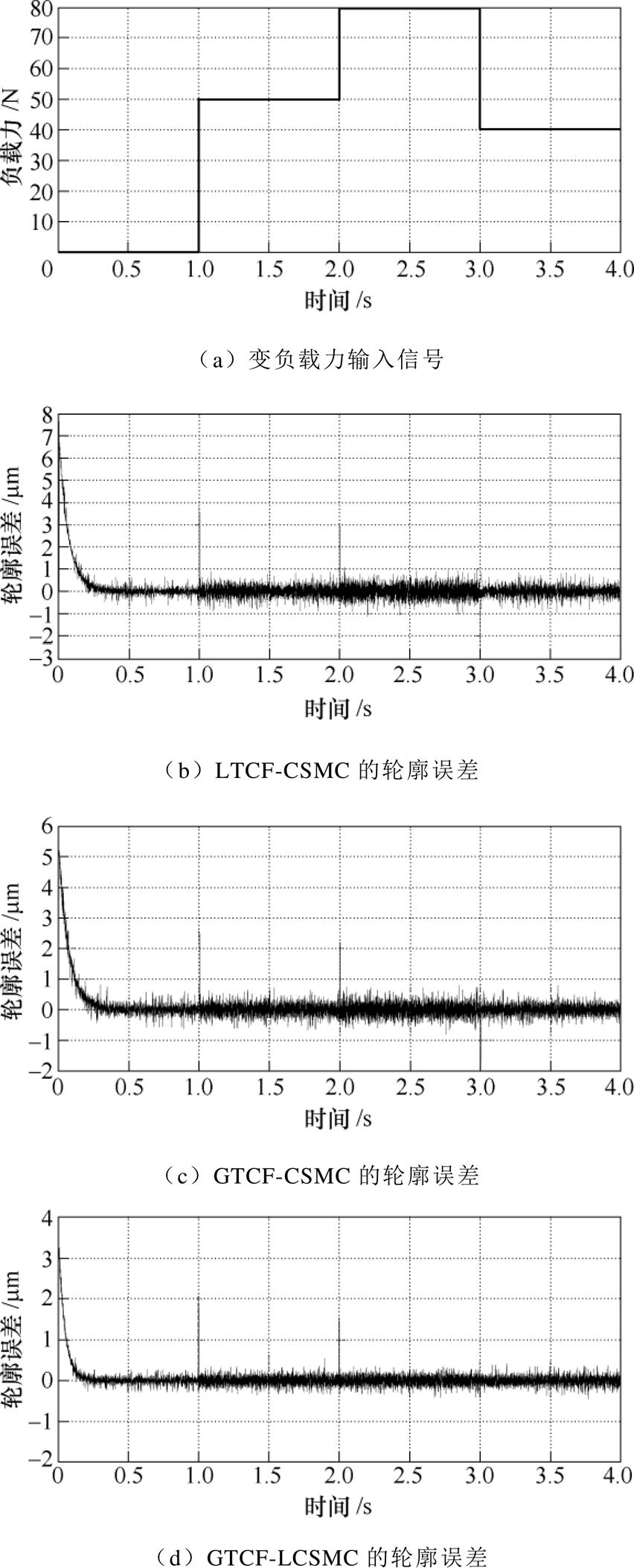
图4 圆形参考轮廓实验结果
Fig.4 Experimental results of circular reference contour
为了进一步考察GTCF-LCSMC的性能,对系统输入xd(t)=0.06cos(pt)和yd(t)=0.02sin(pt)的高速椭圆形轮廓,系统产生的轮廓误差如图5所示。由图5可以看出,LTCF-CSMC产生的轮廓误差最大值为12.5mm,轮廓误差的方均根值为1.68mm,收敛时间为0.61s;GTCF-CSMC产生的轮廓误差最大值为7.6mm,轮廓误差的方均根值为0.79mm,收敛时间为0.45s;GTCF-LCSMC产生的轮廓误差最大值为4.8mm,轮廓误差的方均根值为0.39mm,收敛时间为0.3s,其轮廓误差的方均根值比LTCF-CSMC降低了76.8%且响应速度最快。因此,GTCF-LCSMC对于高速大曲率的轮廓,加工性能更好。
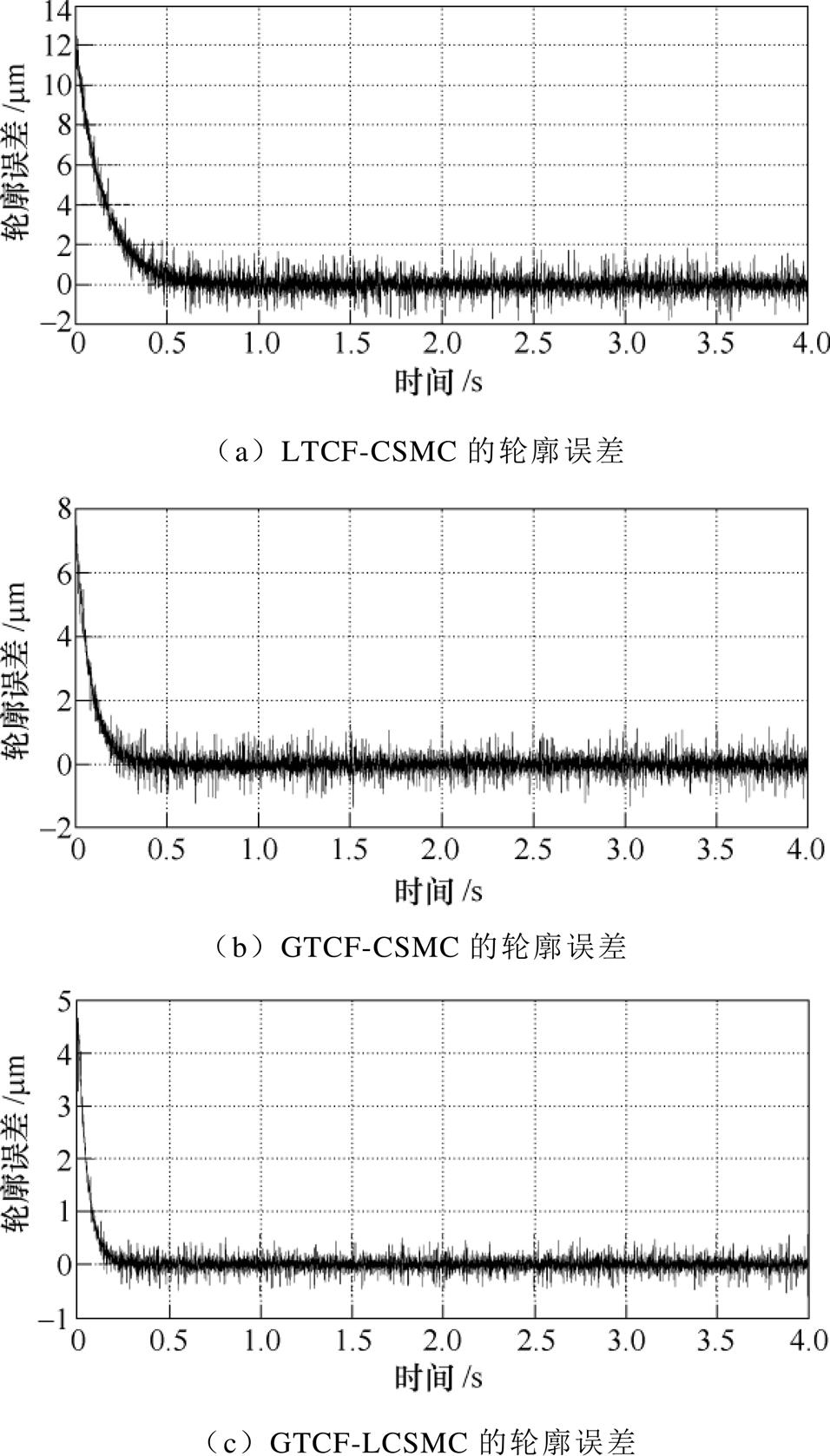
图5 椭圆形参考轮廓实验结果
Fig.5 Experimental results of ellipse reference contour
当系统输入如图6a所示的xd(t)=0.01cos3(pt)和yd(t)=0.01sin3(pt)的星形参考轮廓时,直驱XY平台伺服系统的轮廓误差曲线如图6b~图6d所示。从图中可以看出,在曲线的平滑处,三种控制方案都可以产生良好的跟踪轮廓;LTCF-CSMC在尖角处产生的最大轮廓误差约为9.7mm,轮廓跟踪性能不佳;GTCF-CSMC在尖角处产生的最大轮廓误差约为5mm;GTCF-LCSMC在尖角处产生的最大轮廓误差约为3.3mm,可以更精确地跟踪尖角处的参考轮廓,因此该控制方案有效可行。
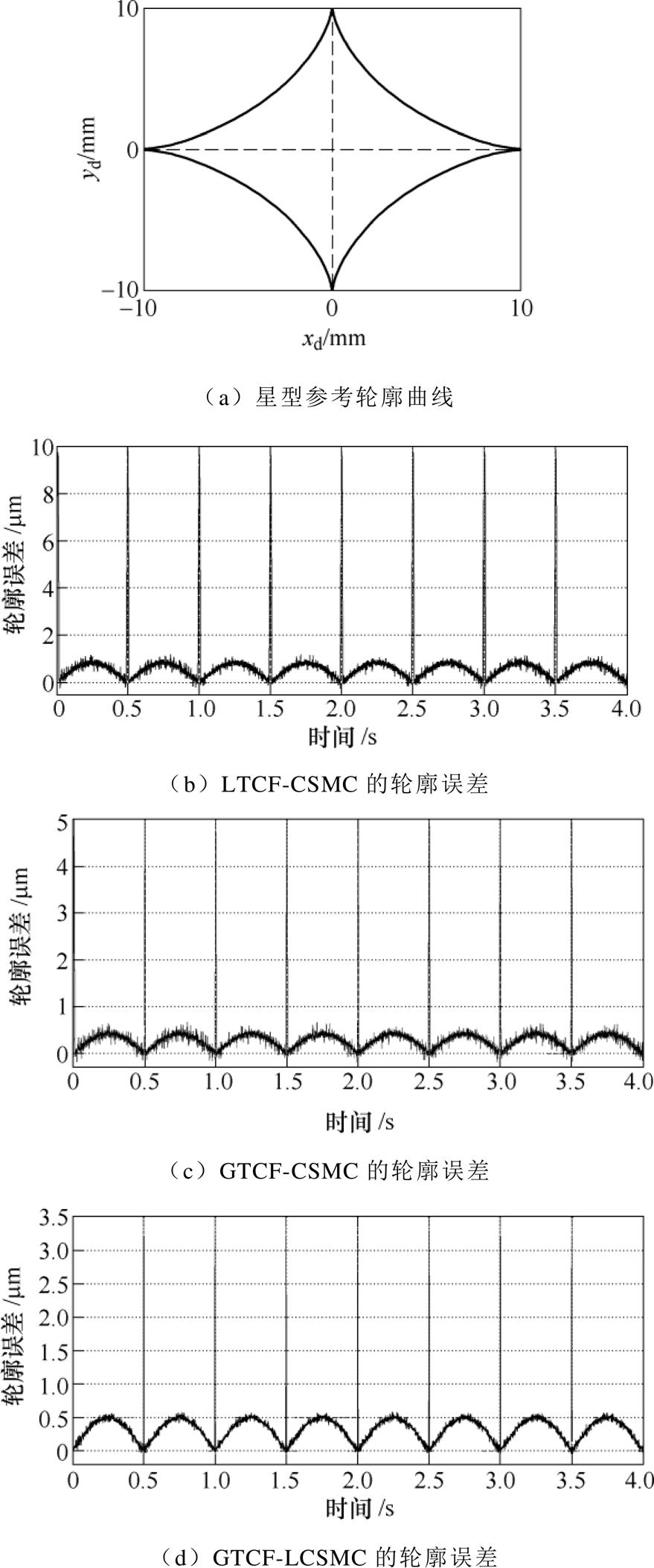
图6 星形参考轮廓实验结果
Fig.6 Experimental results of astroid reference contour
为实现直驱XY平台伺服系统的高精密轮廓控制,考虑到高速大曲率和尖角轮廓使得系统轮廓精度变低这一问题,提出了一种GTCF-LCSMC的精密轮廓控制方案。GTCF可以实现双轴的协调控制;ILC对参考轮廓进行修正并采用CSMC对系统中的不确定性进行控制。从理论上分析了ILC的收敛性与CSMC的稳定性。实验结果表明,本文所采用的控制方案显著减小了系统的轮廓误差且大大提高了系统的响应速度,实现了高精密轮廓控制。
参考文献
[1] 原浩, 赵希梅. 基于动态轮廓误差估计的双轴直驱平台精密轮廓控制[J]. 电工技术学报, 2019, 34(21): 4037-4043.
Yuan Hao, Zhao Ximei. Precision contouring control based on dynamic contouring error estimation for dual axis direct drive platform[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4474- 4480.
[2] 武志涛, 杨永辉. 一种永磁直线电机驱动X-Y平台精密轮廓跟踪控制策略[J]. 电工技术学报, 2018, 33(17): 4037-4043.
Wu Zhitao, Yang Yonghui. A precise contour tracking control method for X-Y table driven by permanent magnet linear motors[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4037- 4043.
[3] Hanifzadegan M, Nagamune R. Contouring control of CNC machine tools based on linear parameter- varying controllers[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(5): 2522-2530.
[4] 赵希梅, 赵久威, 李洪谊. 基于GPC和DOB的直驱XY平台鲁棒跟踪控制[J]. 电工技术学报, 2015, 30(6): 150-154.
Zhao Ximei, Zhao Jiuwei, Li Hongyi. Robust tracking control for direct drive XY table based on GPC and DOB[J]. Transactions of China Electro- technical Society, 2015, 30(6): 150-154.
[5] Li Ming, Zhu Yu, Yang Kaiming, et al. An integrated model-data based zero phase error tracking feed- forward control strategy with application to an ultra-precision wafer stage[J]. IEEE Transactions on Industrial Electronics, 2016, 64(5): 4139-4149.
[6] 王丽梅, 张宗雪. H型精密运动平台交叉耦合模糊PID同步控制[J]. 沈阳工业大学学报, 2018, 40(1): 1-5.
Wang Limei, Zhang Zongxue. Cross-coupled fuzzy PID synchronous control for H-type precision motion platform[J]. Journal of Shenyang University of Tech- nology, 2018, 40(1): 1-5.
[7] Yeh S S, Hsu P L. Estimation of the contouring error vector for the cross-coupled control design[J]. IEEE/ ASME Transactions on Mechatronics, 2002, 7(1): 44-51.
[8] Yang Jiangzhao, Li Zexiang. A novel contour error estimation for position loop-based cross-coupled control[J]. IEEE/ASME Transactions on Mechatro- nics, 2011, 16(4): 643-655.
[9] Chen S L, Wu K C. Contouring control of smooth paths for multiaxis motion systems based on equivalent errors[J]. IEEE Transactions on Control Systems Technology, 2007, 15(6): 1151-1158.
[10] Hu Chuxiong, Wang Ze, Zhu Yu, et al. Performance oriented precision LARC tracking motion control of a magnetically levitated planar motor with comparative experiments[J]. IEEE Transactions on Industrial Electronics, 2016, 63(9): 5763-5773.
[11] Ghaffari A, Ulsoy A G. Dynamic contour error estimation and feedback modification for high- precision contouring[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(3): 1732-1741.
[12] 朱国昕, 雷鸣凯, 赵希梅. 永磁同步电机伺服系统自适应迭代学习控制[J]. 沈阳工业大学学报, 2018, 40(1): 6-11.
Zhu Guoxin, Lei Mingkai, Zhao Ximei. Adaptive iterative learning control for permanent magnet synchronous motor servo system[J]. Journal of Shenyang University of Technology, 2018, 40(1): 6-11.
[13] 赵希梅, 金鸿雁. 基于Elman神经网络的永磁直线同步电机互补滑模控制[J]. 电工技术学报, 2018, 33(5): 973-979.
Zhao Ximei, Jin Hongyan. Complementary sliding mode control for permanent magnet linear syn- chronous motor based on Elman neural network[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 973-979.
Learning Complementary Sliding Mode Contouring Control Based on Global Task Coordinate Frame for Direct Drive XY Table
Abstract A contouring control scheme was proposed for direct drive XY table combining iterative learning control (ILC) and complementary sliding mode control (CSMC) in the global task coordinate frame (GTCF), in order to solve the problem of poor precision when processing high speed or sharp corner contours. Firstly, the error model was constructed by the derivative of actual contouring error. The contouring error and trajectory are used as control variables to establish the GTCF, which enables the system to operate in coordination. Then, the unmodelled dynamics in the contouring tracking process were compensated by ILC, and CSMC was used to suppress the influence of uncertainties such as parameters changing, external disturbances and so on in the direct drive XY table servo system. Finally, the system experimental results show that the proposed method has strong robustness and fast contouring tracking performance. It can achieve more accurate control performance, reduce the contouring error, and improve the high precision contouring machining performance of the direct drive XY table servo system.
keywords:Direct drive XY table, global task coordinate frame, iterative learning control, com- plementary sliding mode control, contouring control
中图分类号:TP273; TM351
DOI: 10.19595/j.cnki.1000-6753.tces.190039
原 浩 男,1992年生,博士研究生,研究方向为直线伺服、智能控制等。E-mail: yuanhao_sut@163.com
赵希梅 女,1979年生,教授,博士生导师,研究方向为电机控制、机器人控制、智能控制等。E-mail: zhaoxm_sut@163.com(通信作者)
收稿日期2019-01-12
改稿日期 2019-06-27
辽宁省自然科学基金计划重点项目(20170540677)和辽宁省教育厅科学技术研究项目(LQGD2017025)资助。
(编辑 赵 鹏)