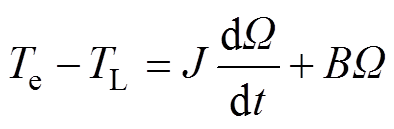 (1)
(1)摘要 针对传统永磁同步电机转速环PI控制下转速跟踪性能差的问题,设计一种复合PI无位置传感器应用于表贴式永磁同步电机转速环控制系统。在传统PI控制的基础上,转速环采用积分钳位型抗积分饱和方法,增加给定输入微分前馈环节和控制增益环节,增强转速环系统跟踪响应性能。分析无阻尼自然频率和阻尼比两者参数选取对系统转矩扰动和角速度测量噪声抑制能力的影响,证明系统抗转矩扰动性能与抑制噪声性能之间存在矛盾。针对该问题,设计以电机转子角速度为状态变量的新型滑模观测器对角速度进行观测,将其直接引入至转速闭环系统反馈,避免角速度反馈噪声对转速跟踪性能造成影响。实验结果验证了该理论分析的正确性与控制策略的可行性。
关键词:表贴式永磁同步电机 复合PI控制 微分前馈 控制增益 滑模观测器
永磁同步电机因功率密度高、运行可靠等优点被广泛应用于诸多工业领域,在其控制算法中,PI控制因结构简单、算法易实现而占据主导地位[1]。然而,永磁同步电机具有多变量、非线性、强耦合的特点,并且在其运行过程中,负载转矩实时变化,传统的PI控制技术已无法满足工业自动化对时变转速实时跟踪性和鲁棒性的要求[2-3]。与此同时,转速闭环系统中,实际转速反馈大多通过对位置传感器检测的转子机械角度进行微分来间接获取。该方法存在三大弊端[4-5]:①使用位置传感器增大了电机体积,提高了成本;②复杂环境下位置传感器易出现故障,系统可靠性降低;③位置传感器检测的转子机械角度存在量化误差,使得对其微分得到的实际转速反馈存在测量噪声,影响闭环系统的跟踪性能。因此,需摒弃位置传感器的使用,增强闭环系统转速反馈的准确性。
为实现永磁同步电机高性能控制,其控制系统内的转速外环和电流内环均需对其相应指令实时跟踪,并且对外部干扰具备较强的鲁棒性。由于电流内环系统跟踪性能只与电机内部参数有关,与外部负载扰动无关,往往需通过精确数学模型计算输出电压给定即可达到良好的电流跟踪效果,因此实际工程应用中,电流环参数一旦确定,则适用于各种工况场合,参数无需二次调整。而对于转速外环系统,会受到时变转速给定和时变负载等不确定性外部扰动,要达到转速实时跟踪目的较为困难,其控制方法主要包括PI控制[6-7]、滑模控制[8-9]、内模控制[10-11]、自抗扰控制[12-13]以及二自由度控制[14]等。实际永磁同步电机高性能调速系统中,控制策略仍然以PI控制为主。对于PI控制,其参数整定对于系统跟踪性能和抗扰性能至关重要。文献[15]提出一种变给定增益PI控制器,通过计算给定变化率自动选择对应的最优增益,进而达到良好的转速跟踪性能。然而,由于系统的PI控制器增益实时变化,无法避免给定转速变化下的系统转速波动。为了提高系统抗外部负载干扰性能,文献[16]利用非线性扰动观测器来估计负载转矩,进而对分数阶PI参数进行自适应调节。该方法虽具有一定效果,但设计过程中需考虑众多非理想因素,算法较复杂、工程实用性不高。文献[17]针对柔性负载下PI参数整定困难问题,分析了PI调节器参数与系统零极点的关系,提出基于极点配置的PI调节器参数整定方法,有效地削弱了柔性负载下的机械振动。然而,该方法中的PI参数整定只针对系统的机械振动问题,对系统连续变化输入的跟踪性能尚未考虑。
本文针对传统永磁同步电机转速环PI控制下转速跟踪性能差的问题,设计了一种复合PI控制器应用于表贴式永磁同步电机(Surface Permanent Magnet Synchronous Motor, SPMSM)转速环控制系统。在传统PI控制的基础上,转速环采用积分钳位型抗积分饱和方法,增加给定输入微分前馈环节和控制增益环节,简化PI参数整定过程,增强转速环系统跟踪响应性能。在此基础上,分析无阻尼自然频率和阻尼比两者参数选取对系统转矩扰动和角速度测量噪声抑制能力的影响,证明系统抗转矩扰动性能与抑制噪声性能之间存在矛盾,需摒弃位置传感器。当前无位置传感器控制大多首先通过滑模观测器观测到电机两相静止坐标系下的反电动势,对其反正切处理以间接获得转子位置和转速。该方法通过两相反电动势间接计算转子位置以及转速,同样避免不了反馈噪声的影响。针对该问题,本文设计以电机转子机械角速度为直接状态变量的新型滑模观测器,对角速度值进行观测,将其直接引入至转速环闭环系统作为反馈,避免角速度反馈噪声对转速跟踪性能造成影响。实验结果验证了所提控制方法的正确性。
永磁同步电机机械运动方程可以表示为
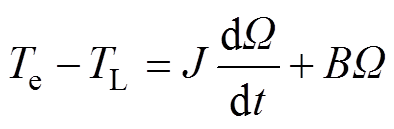 (1)
(1)式中,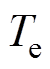 、
、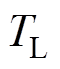 分别为电机输出电磁转矩和负载转矩;
分别为电机输出电磁转矩和负载转矩;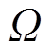 为转子机械角速度;
为转子机械角速度;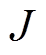 为转动惯量;
为转动惯量;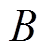 为黏滞摩擦因数。
为黏滞摩擦因数。
对式(1)做相应变换,得到
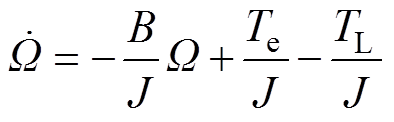 (2)
(2)对于表贴式永磁同步电机,有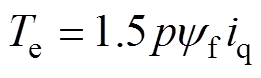 ,其中,p为电机极对数;
,其中,p为电机极对数;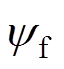 为转子磁链给定;
为转子磁链给定;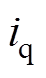 为交轴转矩电流实际值。将式(2)继续变换为
为交轴转矩电流实际值。将式(2)继续变换为
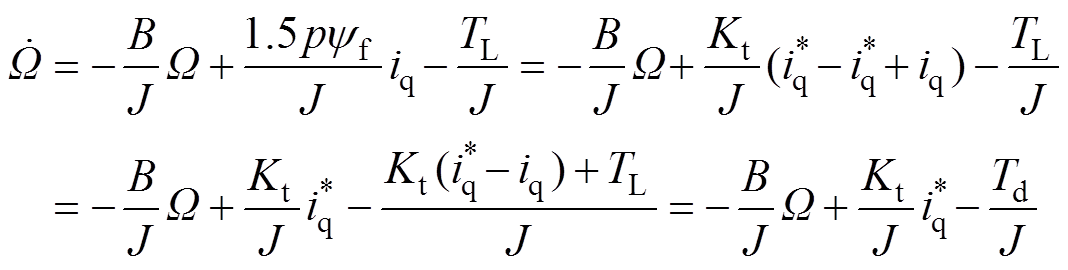 (3)
(3)
式中,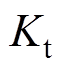 为表贴式永磁同步电机电磁转矩系数,
为表贴式永磁同步电机电磁转矩系数,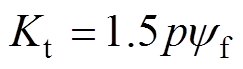 ;
;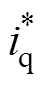 为转矩电流给定;
为转矩电流给定;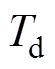 为总转矩扰动,包括负载转矩项和转矩电流控制误差引起的转矩扰动项,
为总转矩扰动,包括负载转矩项和转矩电流控制误差引起的转矩扰动项,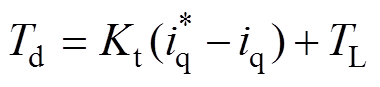 。令状态系数as=
。令状态系数as= ,控制增益
,控制增益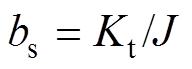 ,扰动项
,扰动项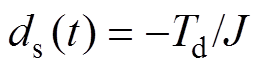 ,则式(3)可简化为
,则式(3)可简化为
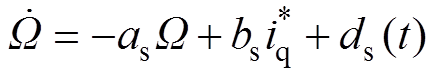 (4)
(4)考虑到黏滞摩擦因数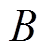 极小,则有
极小,则有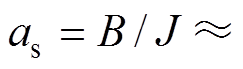
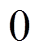 ,式(4)进一步简化为
,式(4)进一步简化为
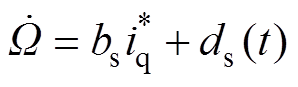 (5)
(5)
定义转子机械角速度跟踪误差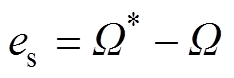 ,
,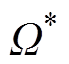 为转子机械角速度给定。建立以机械角速度跟踪误差为状态变量的状态方程,得到
为转子机械角速度给定。建立以机械角速度跟踪误差为状态变量的状态方程,得到
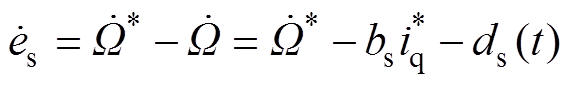 (6)
(6)若转速环控制器采用线性比例积分反馈控制律,即
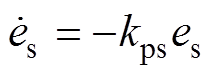 (7)
(7)
式中, 为转速环控制器比例系数,结合式(6)和式(7),得到转速环控制器下的输出转矩电流给定为
为转速环控制器比例系数,结合式(6)和式(7),得到转速环控制器下的输出转矩电流给定为
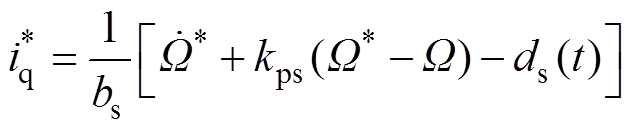 (8)
(8)在有位置传感器永磁同步电机控制系统中,转子机械角速度实际值通过对位置传感器检测到的转子机械角度进行微分获取。然而,由于检测到的转子机械角度存在量化误差等原因,使得微分得到的实际角速度存在测量噪声,即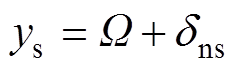 ,其中,
,其中,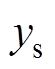 为通过位置传感器间接获取到的角速度反馈,
为通过位置传感器间接获取到的角速度反馈,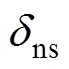 为角速度
为角速度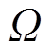 的测量噪声,则转子机械角速度跟踪误差变为
的测量噪声,则转子机械角速度跟踪误差变为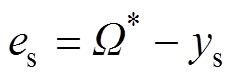 。通过引入积分器抵消扰动项
。通过引入积分器抵消扰动项 对系统的影响,利用机械角速度跟踪误差的积分替代扰动项,得到转速环PI控制器下的输出转矩电流给定为
对系统的影响,利用机械角速度跟踪误差的积分替代扰动项,得到转速环PI控制器下的输出转矩电流给定为
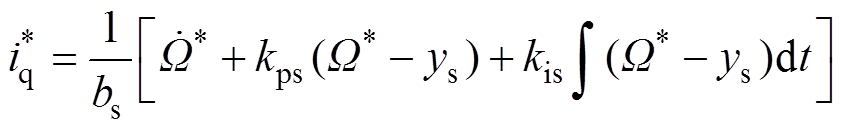 (9)
(9)
对电机输出电磁转矩进行限幅处理,则限幅后的转矩电流给定为
 (10)
(10)式中,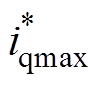 为转矩电流限幅值;sign为符号函数。
为转矩电流限幅值;sign为符号函数。
在传统PI控制的基础上,系统转速环采用积分钳位型抗积分饱和方法,增加给定输入微分前馈环节和控制增益环节。基于此,得到表贴式永磁同步电机转速环复合PI控制结构如图1所示。
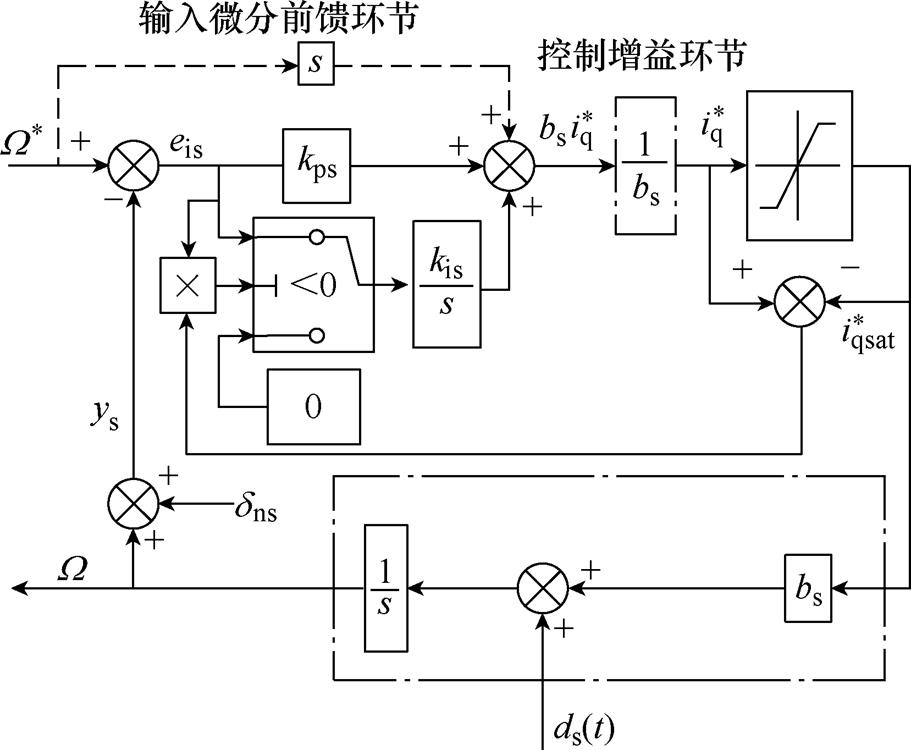
图1 转速环复合PI控制结构
Fig.1 Structure of compound PI control for speed regulation system
将式(9)复合PI控制器输出转矩电流给定代入式(5),得到复合PI控制下的闭环系统输出为
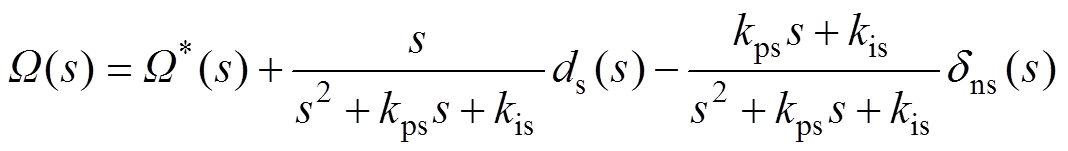 (11)
(11)当系统无输入微分环节时,闭环系统输出变为

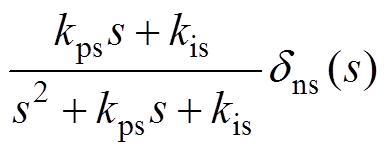 (12)
(12)当系统给定转速输入为连续变化的值时,其输入微分量对应的控制量能够通过系统输入微分前馈环节被及时响应。结合式(11)可得,在无扰动情况下,转速环复合PI控制系统能够无稳态误差地跟踪连续变化输入。
在系统给定转速输入为阶跃信号时,其微分项对应脉冲信号,考虑电流环带宽及电流限幅的影响,阶跃输入信号下微分量对应的控制量无法通过系统输入微分前馈环节被响应,此时输入微分前馈环节不起作用,相当于系统无输入微分环节。根据式(12),复合PI控制在给定作用下表现为二阶系统,令 为典型二阶系统特征多项式
为典型二阶系统特征多项式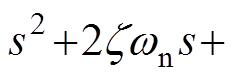
 ,则
,则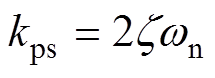 ,
,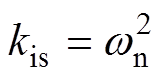 ,其中,
,其中, 为系统阻尼比,
为系统阻尼比,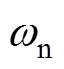 为无阻尼自然频率,得到闭环系统输出为
为无阻尼自然频率,得到闭环系统输出为
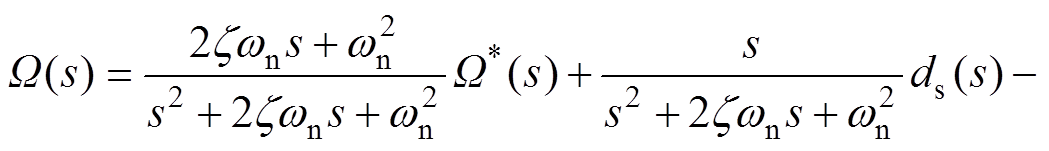
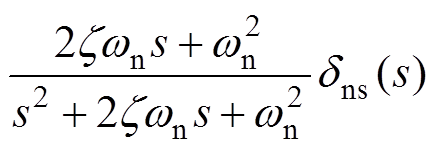 (13)
(13)
由式(13)可得转速闭环系统在转矩扰动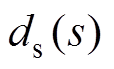 和角速度测量噪声
和角速度测量噪声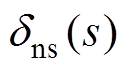 单独作用下的传递函数分别为
单独作用下的传递函数分别为
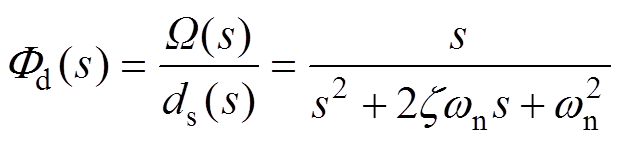 (14)
(14)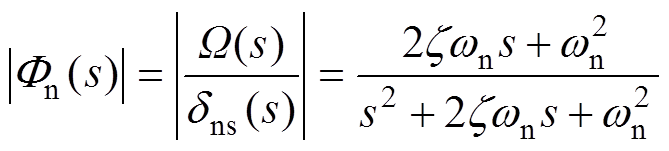 (15)
(15)
式(14)、式(15)可分别表征转矩扰动和角速度测量噪声对转速跟踪性能的影响,为分析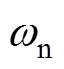 和
和 大小对转矩扰动和测量噪声抑制能力的影响,绘制不同
大小对转矩扰动和测量噪声抑制能力的影响,绘制不同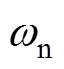 和
和 取值下的转矩扰动和测量噪声传递函数幅频特性曲线如图2和图3所示。根据图2可知,在
取值下的转矩扰动和测量噪声传递函数幅频特性曲线如图2和图3所示。根据图2可知,在 取值相同情况下,低频段
取值相同情况下,低频段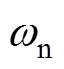 越大,系统对转矩扰动的抑制能力越强;高频段
越大,系统对转矩扰动的抑制能力越强;高频段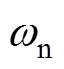 越大,系统对测量噪声的抑制能力越弱。根据图3可知,在
越大,系统对测量噪声的抑制能力越弱。根据图3可知,在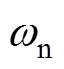 取值相同情况下,在
取值相同情况下,在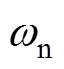 频段附近,
频段附近, 越大,系统对转矩扰动的抑制能力越强;高频段
越大,系统对转矩扰动的抑制能力越强;高频段 越大,系统对测量噪声的抑制能力越弱。由此证明系统抗转矩扰动性能与抑制测量噪声性能之间存在矛盾。鉴于此,设计以角速度为直接状态变量的新型滑模观测器对角速度进行直接观测,避免闭环系统角速度反馈噪声对系统跟踪性能造成影响。
越大,系统对测量噪声的抑制能力越弱。由此证明系统抗转矩扰动性能与抑制测量噪声性能之间存在矛盾。鉴于此,设计以角速度为直接状态变量的新型滑模观测器对角速度进行直接观测,避免闭环系统角速度反馈噪声对系统跟踪性能造成影响。
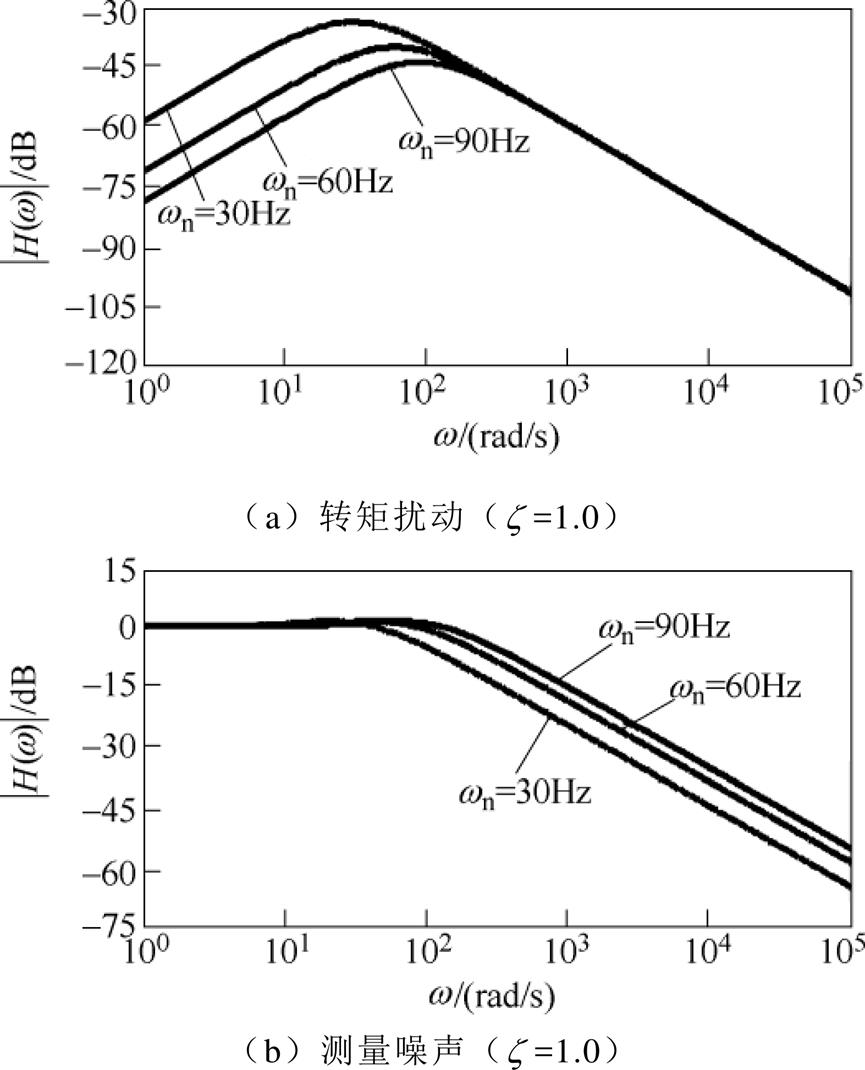
图2 不同 取值下的转矩扰动和测量噪声传递函数幅频特性曲线
取值下的转矩扰动和测量噪声传递函数幅频特性曲线
Fig.2 Torque disturbance and measurement noise transfer function amplitude-frequency characteristic curve at different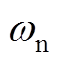
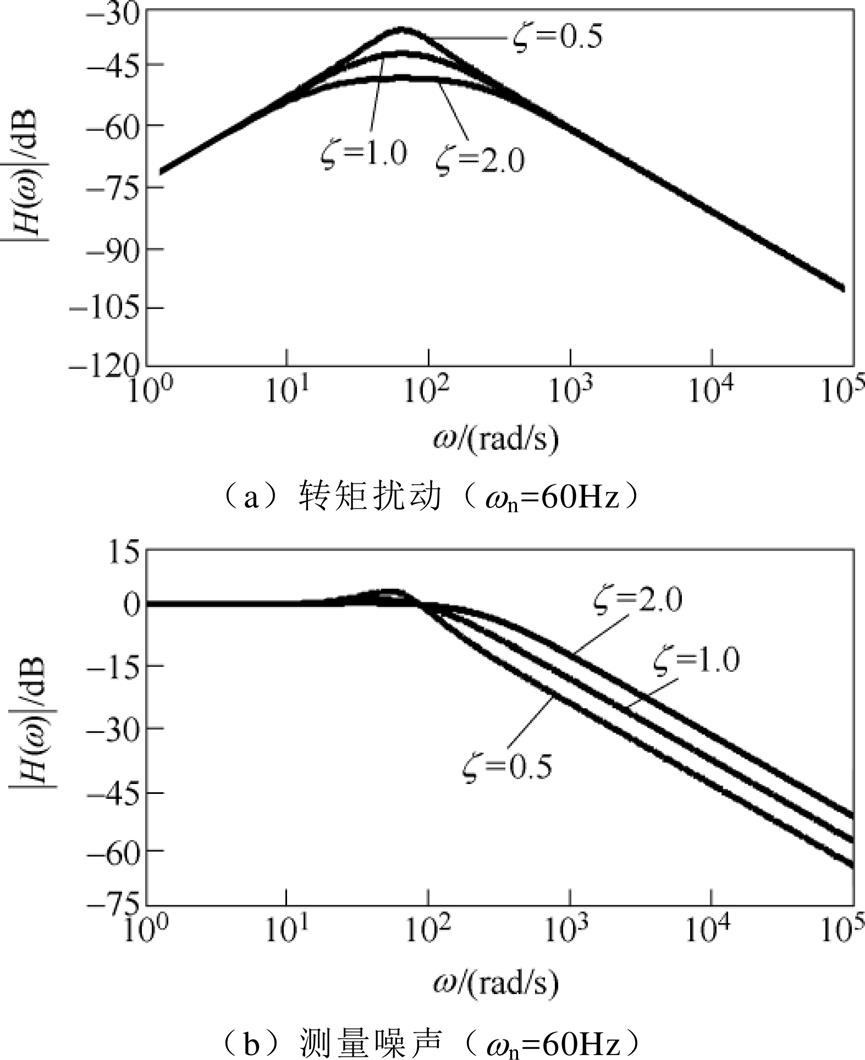
图3 不同 取值下的转矩扰动和测量噪声传递函数幅频特性曲线
取值下的转矩扰动和测量噪声传递函数幅频特性曲线
Fig.3 Torque disturbance and measurement noise transfer function amplitude-frequency characteristic curve at different
以 轴电流
轴电流 、
、 ,转子机械角速度
,转子机械角速度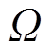 和转子机械角度位置
和转子机械角度位置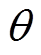 为状态变量建立表贴式永磁同步电机在
为状态变量建立表贴式永磁同步电机在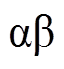 静止坐标系下的状态方程为
静止坐标系下的状态方程为
 (16)
(16)式中,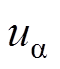 、
、 为
为 轴电压;
轴电压;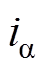 、
、 为
为 轴电流;
轴电流;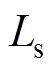 为定子dq轴电感;
为定子dq轴电感; 为定子电阻;
为定子电阻;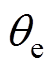 为转子电角度位置,且有
为转子电角度位置,且有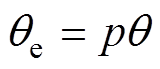 。
。
根据式(16),建立以 轴电流
轴电流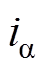 、
、 ,转子机械角速度
,转子机械角速度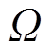 和转子机械角度位置
和转子机械角度位置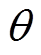 为观测变量的滑模观测器方程为
为观测变量的滑模观测器方程为
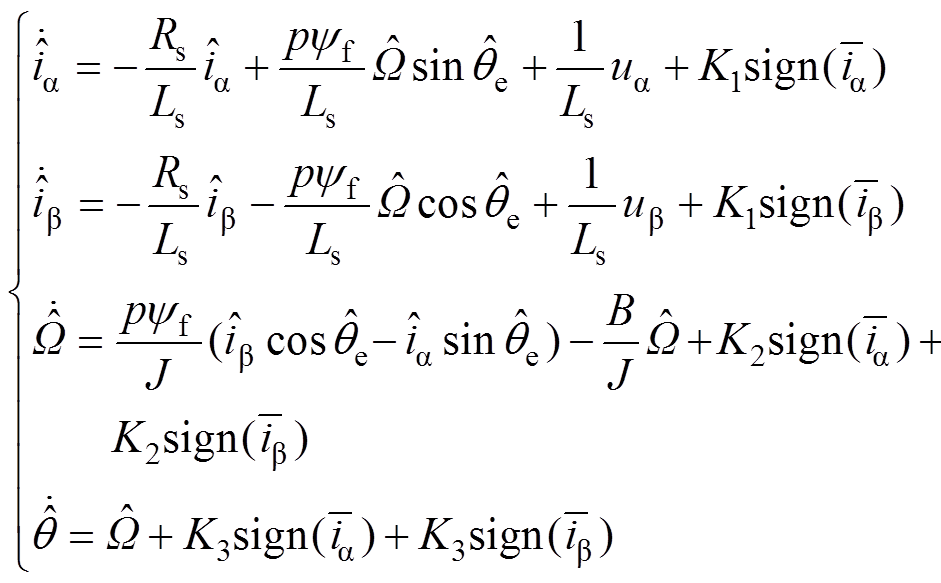 (17)
(17)式中,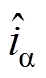 、
、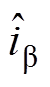 为
为 轴电流观测值;
轴电流观测值;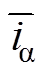 、
、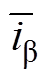 为
为 轴电流观测误差,且有
轴电流观测误差,且有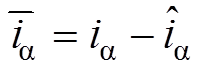 ,
,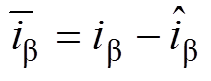 ;
; 为转子机械角速度观测值;
为转子机械角速度观测值; 为转子机械角度位置观测值;
为转子机械角度位置观测值;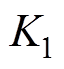 、
、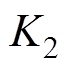 和
和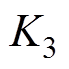 为观测器增益。
为观测器增益。
将式(16)与式(17)相减,得到
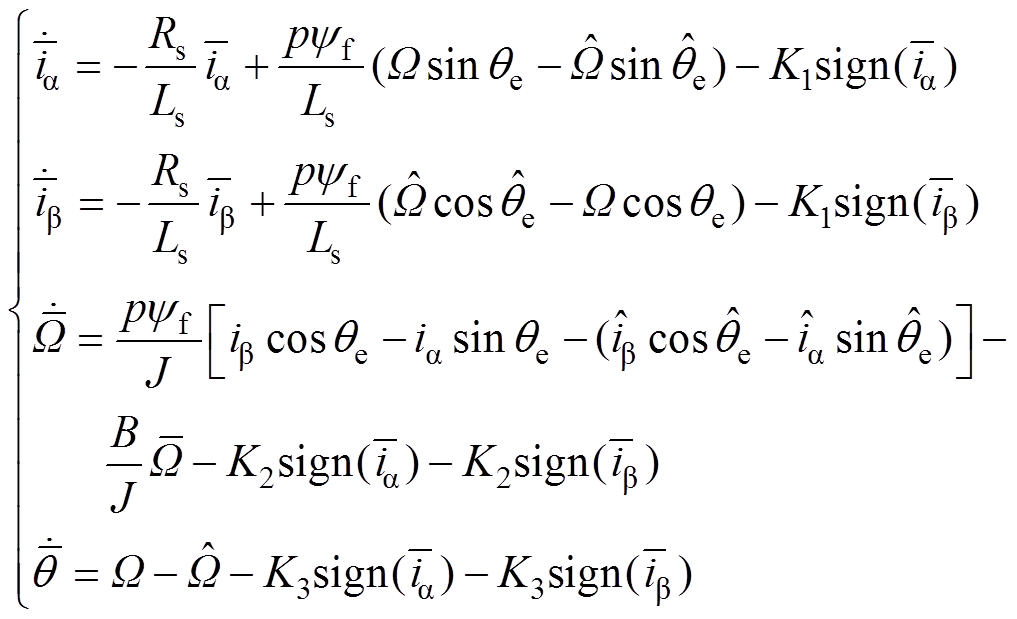 (18)
(18)式中,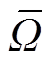 为转子机械角速度观测误差;
为转子机械角速度观测误差;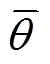 为转子机械角度位置观测误差,且有
为转子机械角度位置观测误差,且有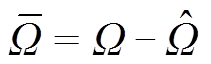 ,
, 。
。
为证明式(17)观测器稳定性,定义Lyapunov函数为
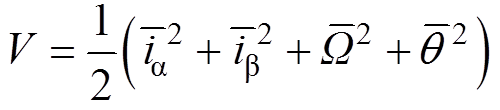 (19)
(19)对式(19)求导,得到
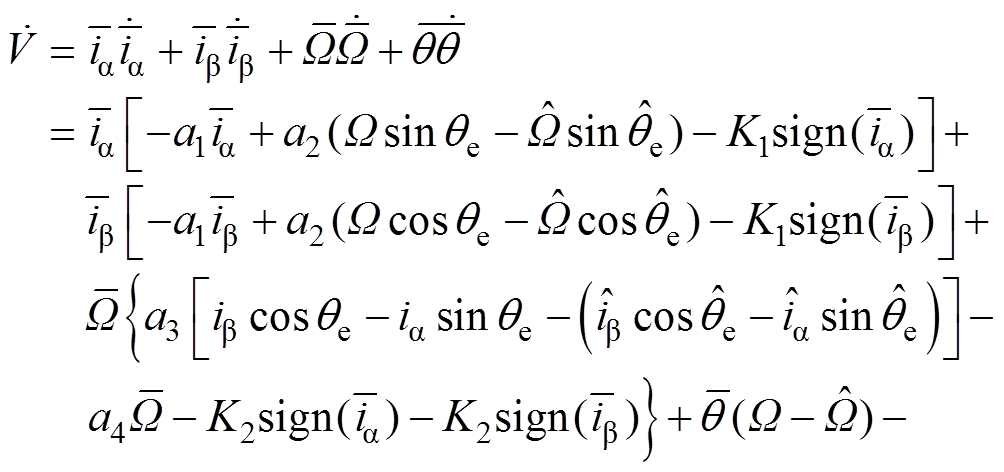
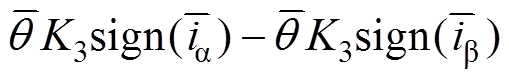 (20)
(20)式中,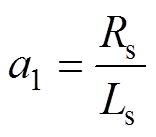 ;
;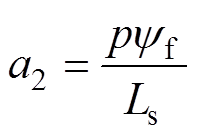 ;
;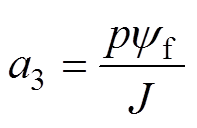 ;
;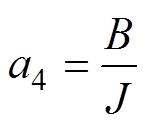 。将式(20)改写成
。将式(20)改写成
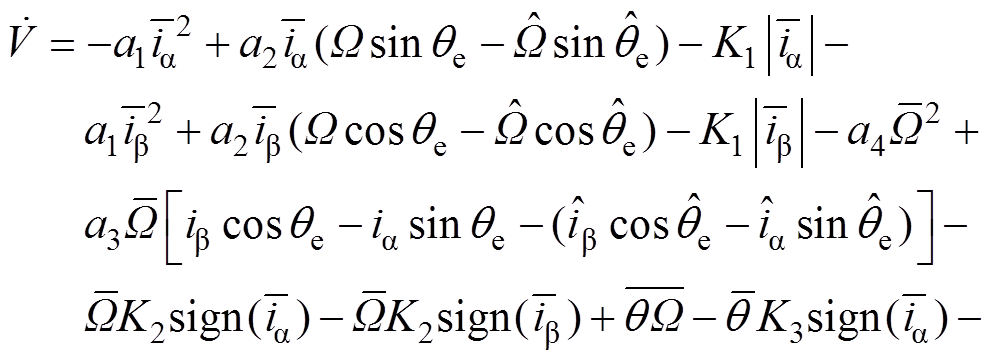
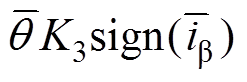 (21)
(21)考虑到
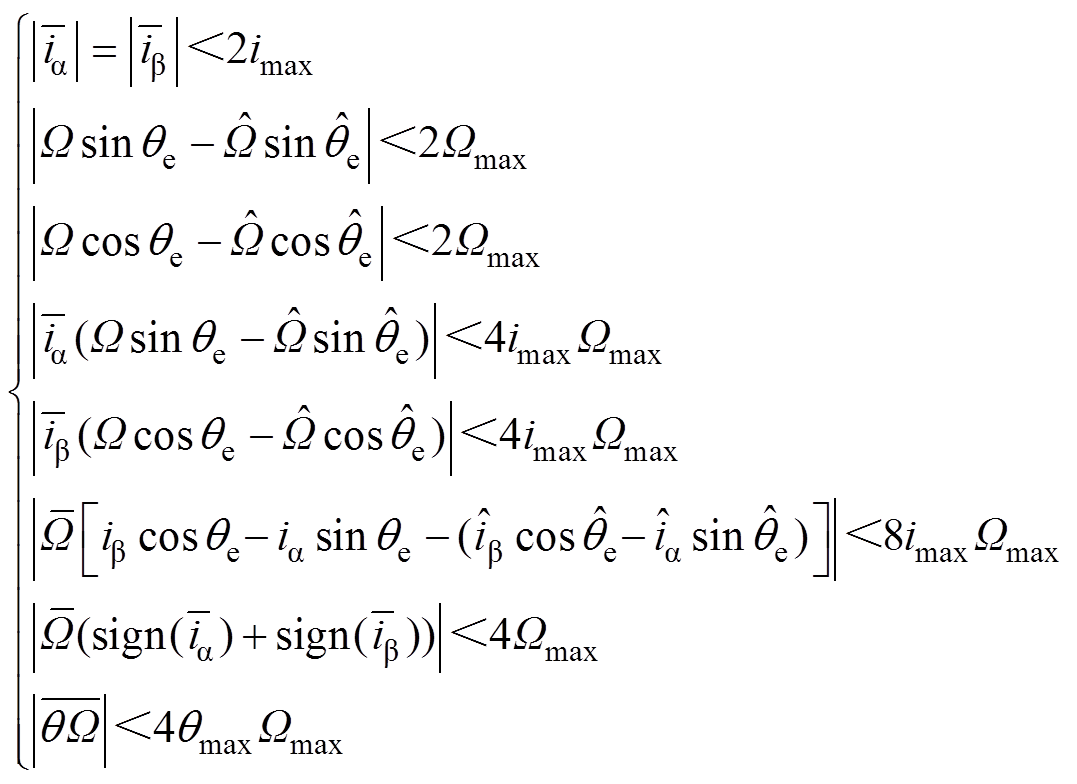 (21)
(21)
式中,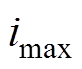 、
、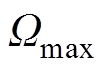 及
及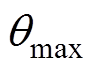 分别为
分别为 轴电流、转子机械角速度及转子机械角度位置最大值。
轴电流、转子机械角速度及转子机械角度位置最大值。
另外,由于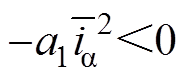 ,
,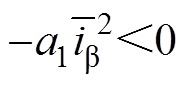 ,
,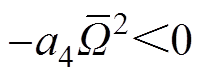 ,选取观测器增益
,选取观测器增益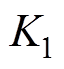 、
、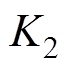 和
和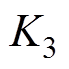 满足
满足
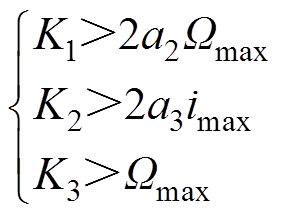 (22)
(22)即可保证观测器稳定。
综上,表贴式永磁同步电机转速环复合PI无位置传感器控制系统结构如图4所示。
为验证转速环复合PI无位置传感器控制策略的有效性,在永磁同步电机交流调速平台上,对本文提出的转速环控制策略进行实验验证,实验电机参数见表1。
相应地,实验平台如图5所示,具体包括被控永磁同步电机、驱动器、磁滞测功机、测功机控制器、PC等。其中,被控永磁同步电机上安装有2 500线的增量式编码器,该编码器起到两个作用:①在有位置传感器下,验证复合PI控制下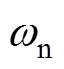 和
和 参数对系统抗扰能力影响分析的正确性;②检测电机的实际转子机械角度位置,并基于此计算电机实际转速,将其与估计转子机械角度位置和估计转速作对比。
参数对系统抗扰能力影响分析的正确性;②检测电机的实际转子机械角度位置,并基于此计算电机实际转速,将其与估计转子机械角度位置和估计转速作对比。

图4 表贴式永磁同步电机转速环复合PI无位置传感器控制系统结构
Fig.4 Structure of sensorless compound PI control for SPMSM speed regulation system
表1 实验电机参数
Tab.1 Parameters of experiment motor

参 数数 值 额定功率/W750 额定电压/V220 额定电流/A4.2 额定转矩/(N·m)2.4 额定转速/(r/min)3 000 定子电阻/W0.901 dq轴电感/mH6.552 极对数4 转动惯量/(kg·m2)

图5 实验平台
Fig.5 Experimental platform
首先,实验中整个永磁同步电机控制系统包括转速环和电流环系统,电流环均采用传统PI控制,转速环将复合PI控制与传统PI控制进行对比。在传统PI控制系统稳定且性能较优的前提下,将转速环PI模块替换为本文提出的复合PI控制模块。通过在芯片代码中写入可调频率和幅值的正弦信号作为系统转速给定,以验证系统转速跟踪响应性能;通过测功机控制器突加、突卸负载转矩,用于模拟外部负载扰动,以验证系统抗负载扰动的鲁棒性。传统PI控制参数设置为综合考虑超调及响应性能两方面因素下,经过反复调试达到的较优值。
为验证复合PI控制下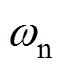 和
和 参数大小对系统抗负载扰动能力影响分析的正确性,在800r/min转速、额定负载工况下突卸负载,如图6所示为突卸负载工况下的转速电流响应波形,该工况下使用编码器获取转子机械角度位置和实际转速。其中, 图6a为
参数大小对系统抗负载扰动能力影响分析的正确性,在800r/min转速、额定负载工况下突卸负载,如图6所示为突卸负载工况下的转速电流响应波形,该工况下使用编码器获取转子机械角度位置和实际转速。其中, 图6a为 ,
,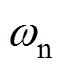 分别取值30Hz、60Hz和90Hz时的转速电流响应波形;图6b为
分别取值30Hz、60Hz和90Hz时的转速电流响应波形;图6b为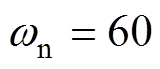 Hz,
Hz, 分别取值0.5、1.0和2.0时的转速电流响应波形。根据6a可知,
分别取值0.5、1.0和2.0时的转速电流响应波形。根据6a可知, 相同时,
相同时,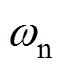 取值越大,负载转矩突变下的转速波动越小,调节时间越短。具体地,当
取值越大,负载转矩突变下的转速波动越小,调节时间越短。具体地,当
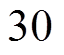 Hz时,转速变化达到40r/min,调节时间达到300ms;而当
Hz时,转速变化达到40r/min,调节时间达到300ms;而当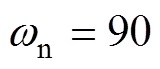 Hz时,转速变化降低为15r/min,调节时间降低为170ms,由此验证
Hz时,转速变化降低为15r/min,调节时间降低为170ms,由此验证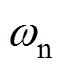 越大,系统对转矩扰动的抑制能力越强。同理,根据图6b可知,
越大,系统对转矩扰动的抑制能力越强。同理,根据图6b可知,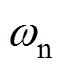 相同时,
相同时, 取值越大,负载转矩突变下的转速波动越小,调节时间越短。具体地,在
取值越大,负载转矩突变下的转速波动越小,调节时间越短。具体地,在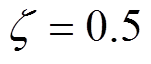 时,转速变化达到32r/min,调节时间同样达到300ms;而当
时,转速变化达到32r/min,调节时间同样达到300ms;而当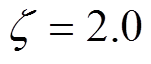 时,转速变化降低为15r/min,调节时间无明显变化,由此验证
时,转速变化降低为15r/min,调节时间无明显变化,由此验证 越大,系统对转矩扰动的抑制能力越强。
越大,系统对转矩扰动的抑制能力越强。
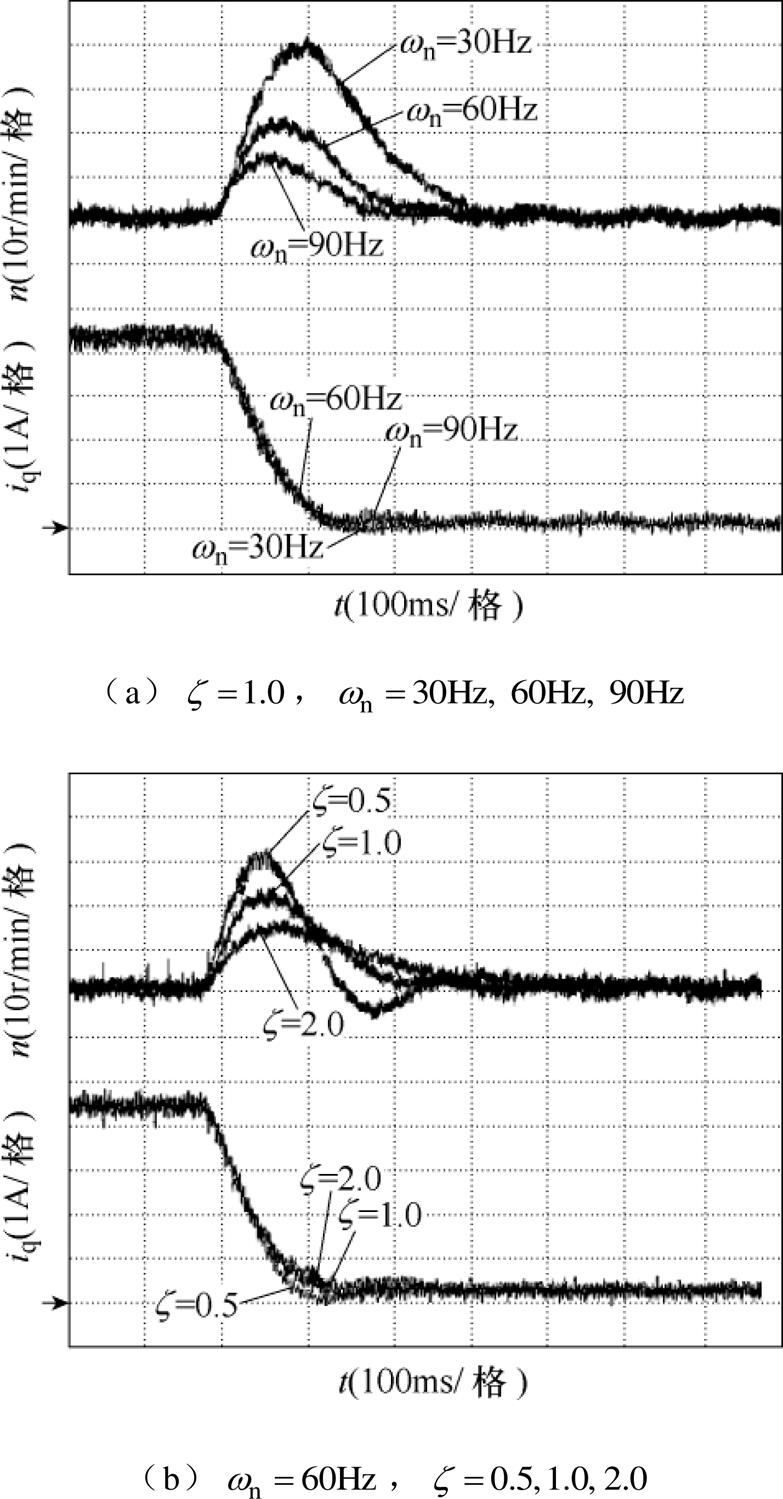
图6 突卸负载工况下的转速电流响应波形
Fig.6 Speed and current response waveforms under sudden unloading load condition
为验证复合PI控制下系统转速跟踪响应性能的优势,将复合PI控制下的转速跟踪响应与传统PI控制进行对比,如图7所示为正弦转速给定下的实际转速及其误差对比。其中给定正弦转速分两种情形:①幅值为500r/min,频率为5Hz,如图7a和图7b所示;②幅值为200r/min,频率为15Hz,如图7c和图7d所示。对比图7a与图7b可知,当给定正弦转速幅值为500r/min,频率为5Hz时,传统PI控制下的转速跟踪存在幅值为10r/min、频率为5Hz的正弦误差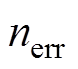 ,而复合PI控制下的转速跟踪误差始终在零附近上下波动,波动值限制在
,而复合PI控制下的转速跟踪误差始终在零附近上下波动,波动值限制在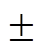 3r/min之内。同理,对比图7c与图7d可知,当给定正弦转速幅值变化为200r/min,频率为15Hz时,传统PI控制下的转速跟踪存在幅值为20r/min、频率为15Hz的正弦误差,而复合PI控制下的转速跟踪误差始终在零附近上下波动,波动值依旧限制在
3r/min之内。同理,对比图7c与图7d可知,当给定正弦转速幅值变化为200r/min,频率为15Hz时,传统PI控制下的转速跟踪存在幅值为20r/min、频率为15Hz的正弦误差,而复合PI控制下的转速跟踪误差始终在零附近上下波动,波动值依旧限制在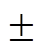 3r/min之内。由此可以验证复合PI控制在系统转速跟踪响应性能方面的优势,其可有效提高系统的转速环响应带宽。
3r/min之内。由此可以验证复合PI控制在系统转速跟踪响应性能方面的优势,其可有效提高系统的转速环响应带宽。
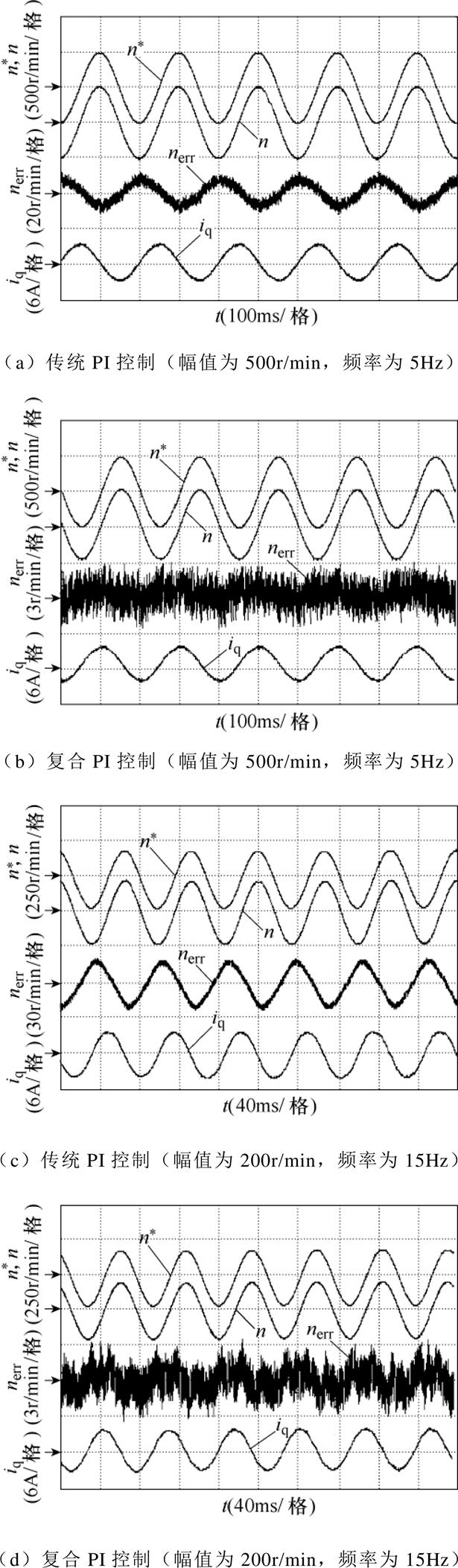
图7 正弦转速给定下的实际转速及其误差对比
Fig.7 Comparison of actual speed and its error under sinusoidal speed given
为验证复合PI控制在抗外部负载扰动性能方面的优势,在额定转速下,通过测功机控制器突加、突卸额定负载,将复合PI控制下的实际转速与传统PI控制进行对比,如图8所示。图8a为传统PI控制下突加额定负载时的转速电流响应波形,在突加额定负载瞬间,实际转速存在25r/min左右的向下波动,经过大约300ms时间恢复至稳态;图8b为复合PI控制下突加额定负载时的转速电流响应波形,在突加额定负载瞬间,实际转速仅存在10r/min左右的向下波动,经过大约200ms时间恢复至稳态;图8c为传统PI控制下突卸额定负载时的转速电流响应波形,在突卸额定负载瞬间,实际转速存在25r/min左右的向上波动,同样经过大约300ms时间恢复至稳态;图8d为复合PI控制下突卸额定负载时的转速电流响应波形,在突卸额定负载瞬间,实际转速存在仅10r/min左右的向上波动,并且经过大约200ms时间恢复至稳态。对比图8a~图8d可知,额定转速下,突加、突卸额定负载瞬间,复合PI控制下的转速波动量仅为传统PI控制下的40%左右,稳态恢复时间较传统PI控制也有所缩短。
如图9所示为系统引入新型滑模观测器,电机在300r/min转速下的转子机械角度位置估计及其电角度误差 。根据图9可知,转子机械角度位置估计严格跟随实际转子位置,其电角度位置估计误差限制在
。根据图9可知,转子机械角度位置估计严格跟随实际转子位置,其电角度位置估计误差限制在 12°之内。
12°之内。
图8 负载突变下的实际转速及转矩电流对比
Fig.8 Comparison of actual speed and torque current under abrupt load change
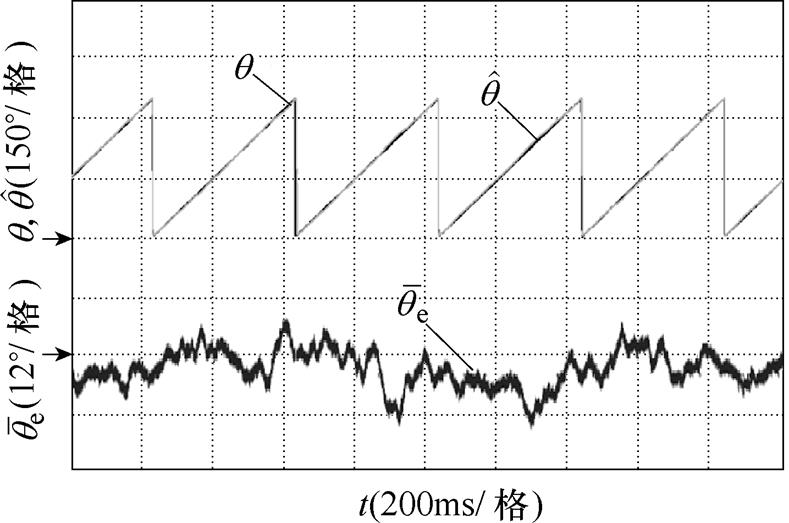
图9 300r/min转速下的转子机械角度位置估计及其电角度误差
Fig.9 Rotor mechanical position estimation and electrical error at 300r/min
如图10所示为转速突变下的响应波形,其中包括转子位置估计误差、实际转速以及估计转速,在3s时刻给定电机转速由500r/min阶跃上升至额定转速,在7s时刻给定电机转速由额定转速阶跃下降至500r/min。编码器获取的转子位置不参与闭环控制,通过新型滑模观测器观测到的转子位置和转速完成闭环系统控制,转速环采用复合PI控制。根据图10可知,当转速给定由500r/min阶跃上升至额定转速时,转子位置估计误差无明显变化,估计转速严格跟随实际转速。当转速给定由额定转速阶跃下降至500r/min时,转子位置估计误差同样无明显变化,估计转速严格跟随实际转速。
同理,图11为负载转矩突变下的响应波形,其中,图11a为突加、突卸负载工况,包括负载转矩、实际转速以及转子位置估计误差,并且电机运行在额定转速工况。图11b为阶梯式突加负载工况,包括负载转矩和转子位置估计误差,并且电机运行在50%额定转速工况。同样,编码器获取的转子位置不参与闭环控制,通过估计转子位置和估计转速完成闭环系统控制,转速环均采用复合PI控制。根据图11a可知,在突加、突卸额定负载瞬间,电机实际转速存在 10r/min左右的波动量,但在0.2s内均恢复稳态,结合图11b可知,负载突变对转子位置估计误差影响较小。
10r/min左右的波动量,但在0.2s内均恢复稳态,结合图11b可知,负载突变对转子位置估计误差影响较小。
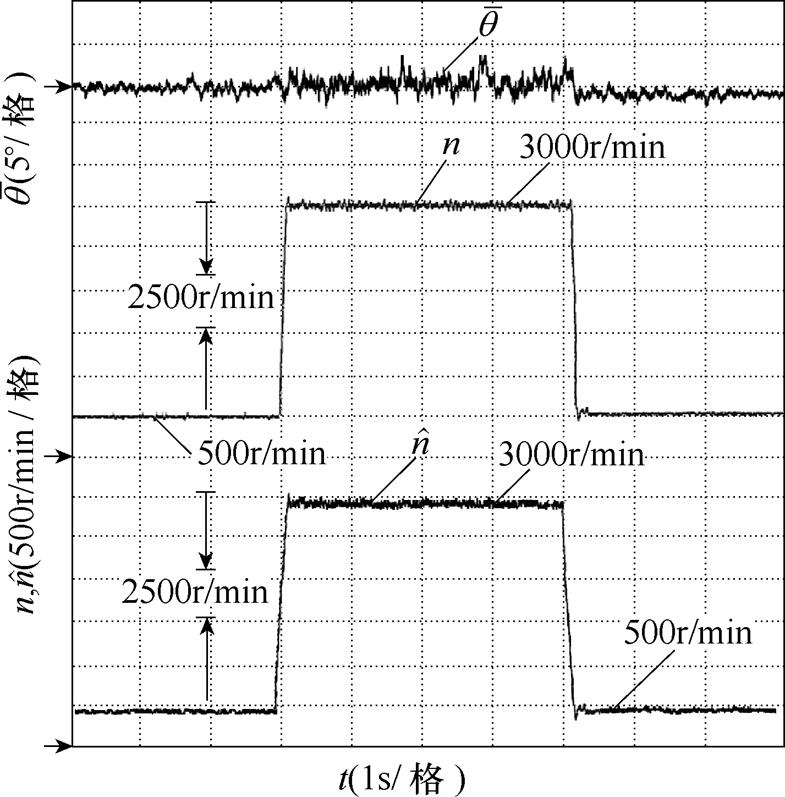
图10 转速突变下的响应波形
Fig.10 Response waveforms under sudden speed change
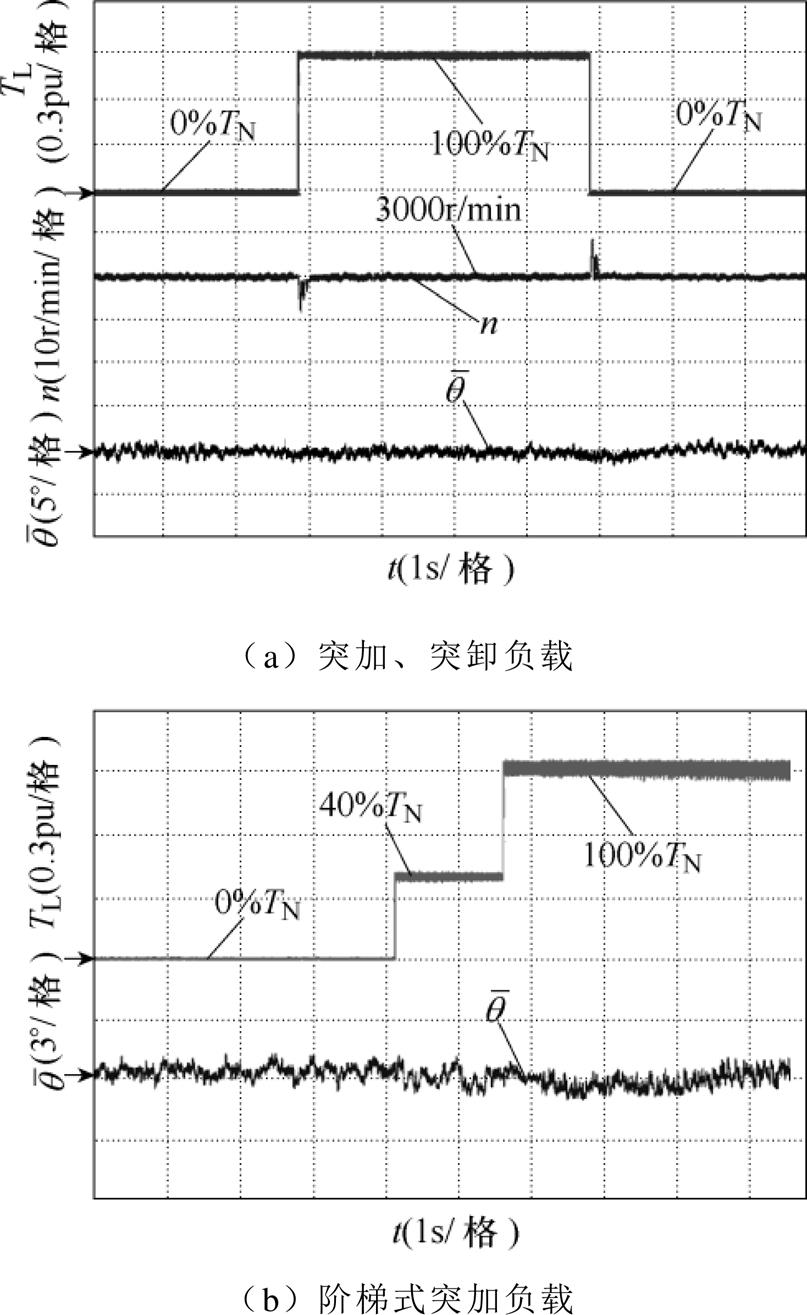
图11 负载突变下的响应波形
Fig.11 Response waveforms under sudden load change
图12为负载、转速突变下的响应波形,其中包括负载转矩、实际转速以及转子位置估计误差。电机空载运行在500r/min,突加额定负载,大约经过4s后,给定电机转速由500r/min阶跃上升至3 000r/min。根据图12可知,负载转矩扰动下,电机实际转速存在较小的波动;转速扰动下,实际转速能够快速跟随给定转速,无明显超调,转子位置估计误差始终无明显变化,进一步验证了转速环复合PI无位置传感器控制对于负载扰动和转速扰动的鲁棒性。
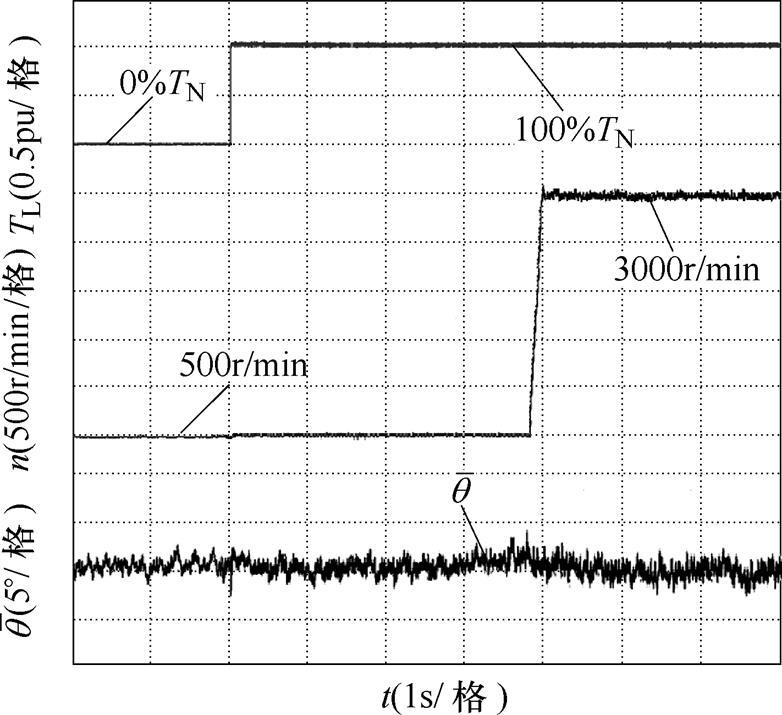
图12 负载、转速突变下的响应波形
Fig.12 Response waveforms under sudden load and speed change
本文设计一种复合PI控制器应用于表贴式永磁同步电机转速环控制系统。在传统PI控制的基础上,增加了给定输入微分前馈环节对连续变化输入及时响应,增强了转速环系统跟踪响应性能。分析了无阻尼自然频率和阻尼比两者参数选取对系统转矩扰动和角速度测量噪声抑制能力的影响,证明了系统抗转矩扰动与抑制噪声之间的矛盾性,为PI控制系统相关参数的选择与优化提供了理论依据。设计了以电机转子机械角速度为直接状态变量的新型滑模观测器对角速度值进行观测,将观测值直接引入至转速闭环系统作为反馈,避免角速度反馈噪声对转速跟踪性能造成影响。
以750W表贴式永磁同步电机为实验对象,对转速环复合PI无位置传感器控制策略下的相应实验波形进行分析研究,实验结果验证了时变输入下复合PI控制相对于传统PI控制优良的跟踪性能,新型控制策略对于转矩扰动和转速扰动有着较强的鲁棒性。另外,考虑到本文控制策略目前只能应用于表贴式永磁同步电机,下一步将重点研究控制策略的普及化以及工程化问题,以期实现其实际工程应用。
参考文献
[1] Errouissi R, Al-Durra A, Muyeen S M. Experimental validation of a novel PI speed controller for AC motor drives with improved transient performances[J]. IEEE Transactions on Control Systems Technology, 2018, 26(4): 1414-1421.
[2] 张海洋, 许海平, 方程, 等. 基于负载转矩观测器的直驱式永磁同步电机新型速度控制器设计[J]. 电工技术学报, 2018, 33(13): 2923-2934.
Zhang Haiyang, Xu Haiping, Fang Cheng, et al. Design of a novel speed controller for direct-drive permanent magnet synchronous motor based on load torque observer[J]. Transactions of China Electro- technical Society, 2018, 33(13): 2923-2934.
[3] 刘宁, 夏长亮, 周湛清, 等. 基于比例增益补偿的永磁同步电机转速平滑控制[J]. 电工技术学报, 2018, 33(17): 4007-4015.
Liu Ning, Xia Changliang, Zhou Zhanqing, et al. Smooth speed control for permanent magnet synchronous motor using proportional gain compensation[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4007-4015.
[4] 朱军, 田淼, 付融冰, 等. 基于载波频率成分的永磁同步电机转子定位研究[J]. 电力系统保护与控制, 2015, 43(14): 48-54.
Zhu Jun, Tian Miao, Fu Rongbing, et al. Research on rotor position of permanent magnet synchronous motor based on carrier frequency component[J]. Power System Protection and Control, 2015, 43(14): 48-54.
[5] Liang Donglai, Li Jian, Qu Ronghai, et al. Adaptive second-order sliding-mode observer for PMSM sensorless control considering VSI nonlinearity[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8994-9004.
[6] 胡勤丰, 陈威振, 邱攀峰, 等. 适用于连续加减速的永磁同步电机模糊增益自调整PI控制研究[J]. 中国电机工程学报, 2017, 37(3): 907-914.
Hu Qinfeng, Chen Weizhen, Qiu Panfeng, et al. Research on fuzzy self-tuning gain PI control for accelerating and decelerating based on permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(3): 907-914.
[7] 彭熙伟, 高瀚林. 永磁同步电机的改进对角递归神经网络PI控制策略[J]. 电机与控制学报, 2019, 23(4): 126-132.
Peng Xiwei, Gao Hanlin. Improved diagonal recur- sion neural network and PI control of permanent magnet synchronous motor[J]. Electric Machines and Control, 2019, 23(4): 126-132.
[8] 崔家瑞, 高江峰, 张波, 等. 永磁同步电机滑模变结构鲁棒控制[J]. 电机与控制学报, 2016, 20(5): 84-89.
Cui Jiarui, Gao Jiangfeng, Zhang Bo, et al. Robust control of synchronous motor based on sliding mode variable structure[J]. Electric Machines and Control, 2016, 20(5): 84-89.
[9] Liu Jing, Li Hongwen, Deng Yongting. Torque ripple minimization of PMSM based on robust ILC via adaptive sliding mode control[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3655-3671.
[10] Li Shihua, Gu Hao. Fuzzy adaptive internal model control schemes for PMSM speed-regulation system[J]. IEEE Transactions on Industrial Informatics, 2012, 8(4): 767-779.
[11] Liu Guohai, Chen Lingling, Zhao Wenxiang, et al. Internal model control of permanent magnet synchronous motor using support vector machine generalized inverse[J]. IEEE Transactions on Industrial Infor- matics, 2013, 9(2): 890-898.
[12] 左月飞, 张捷, 刘闯, 等. 针对时变输入的永磁同步电机改进型自抗扰控制器[J]. 电工技术学报, 2017, 32(2): 161-170.
Zuo Yuefei, Zhang Jie, Liu Chuang, et al. A modified adaptive disturbance rejection controller for per- manent magnetic synchronous motor speed regulation system with time-varying input[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 161-170.
[13] Sira R H, Linares F J, García R C, et al. On the control of the permanent magnet synchronous motor: an active disturbance rejection control approach[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 2056-2063.
[14] 左月飞, 符慧, 刘闯, 等. 永磁同步电机调速系统的一种新型二自由度控制器[J]. 电工技术学报, 2016, 31(17): 140-146.
Zuo Yuefei, Fu Hui, Liu Chuang, et al. A novel two- degree-of-freedom controller for permanent magnetic synchronous motor speed-regulation system[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 140-146.
[15] 符慧, 左月飞, 刘闯, 等. 永磁同步电机调速系统的一种变给定增益PI控制器[J]. 电工技术学报, 2017, 32(1): 168-174.
Fu Hui, Zuo Yuefei, Liu Chuang, et al. A variable input gain proportional integral controller for per- manent magnetic synchronous motor speed-regulation system[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 168-174.
[16] Apte A, Thakar U, Joshi V. Disturbance observer based speed control of PMSM using fractional order PI controller[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(1): 316-326.
[17] 丁有爽, 肖曦. 基于极点配置的永磁同步电机驱动柔性负载PI调节器参数确定方法[J]. 中国电机工程学报, 2017, 37(4): 1125-1138.
Ding Youshuang, Xiao Xi. Parameter tuning methods based on pole placement for PI controllers of flexible loads driven by PMSM[J]. Proceedings of the CSEE, 2017, 37(4): 1125-1138.
Sensorless Compound PI Control for Surface Permanent Magnet Synchronous Motor Speed Regulation System
Abstract Traditional speed loop PI control of permanent magnet synchronous motor (PMSM) has poor speed tracking performance. Aiming at this problem, a compound PI controller is designed for the speed loop control system of surface PMSM (SPMSM). On the basis of traditional PI control, the integral clamping anti-integral saturation method is adopted in the speed loop, and the given input differential feedforward link and control gain link are added to enhance the tracking response performance of the speed loop system. The influence of the parameters of undamped natural frequency and damping ratio on the system's torque disturbance and angular speed measurement noise suppression ability is analyzed, which proves there is a contradiction between anti-torque disturbance and noise suppression performance of the system. For this reason, a new sliding mode observer (SMO) with speed as the state variable is designed to observe the motor speed, which is directly introduced into the closed-loop speed feedback system to avoid the influence of speed feedback noise on speed tracking performance. The experimental results verify the correctness of the theoretical analysis and the feasibility of the control strategy.
keywords:Surface permanent magnet synchronous motor, compound PI control, differential feedforward, control gain, sliding mode observer
中图分类号:TM301
DOI: 10.19595/j.cnki.1000-6753.tces.190380
李垣江 男,1981年生,博士,研究方向为电机驱动控制以及复杂控制系统。E-mail: liyuanjiang@just.edu.cn(通信作者)
董 鑫 男,1994年生,硕士,研究方向为永磁同步电机无传感器控制。E-mail: 215962529@qq.com
收稿日期 2019-04-04
改稿日期 2019-07-09
国家自然科学基金(51809128)和江苏省省重点研发计划产业前瞻与共性关键技术重点(BE2018007)资助项目。
(编辑 陈 诚)