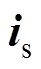和
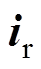分别为定、转子电流矢量；
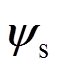和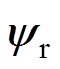
分别为定、转子磁链矢量；
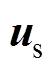定子端电压矢量；各物理参数均表示为折算到定子侧的实际值，Rs和Rr分别为定、转子侧绕组电阻；Lls和Llr分别为定、转子侧绕组漏电感；M为定、转子绕组间的互感，即励磁电感，且定、转子绕组自感分别为Ls=M +Lls、Lr=M +Llr；C为励磁电容；Rl为电阻负载；w 为转子转速，且保持不变。因M为励磁电流的非线性函数，该等效电路为非线性电路。摘要 为了解析计算出自励异步发电机带载建压励磁电容值，首先，建立其基于静止两相正交参考坐标系下的空间矢量暂态等效电路及其数学模型。然后，提出一种系统稳定性的等价转换分析方法，得到表征系统能量平衡和运动稳定的准极限环临界条件。再次，计算准极限环临界条件，得到给定转子转速和电阻情况下带载建压励磁电容临界值解析解，进一步得到给定励磁电容和电阻情况下带载建压转子转速临界值解析解，以及确保自励的必要条件：电阻和励磁电容限值的解析解。最后，与其他方法和模型仿真对不同工况进行比较，验证该文方法的正确性、高效性和通用性，并证明该文方法适于更复杂系统的分析，解析式具有工程参考价值，有助于系统优化配置和性能评估。
关键词：自励异步发电机 暂态等效电路 空间矢量模型 暂态稳定性 解析式
作为目前新能源发电的重要方式[1]，自励异步发电机（Self-Excited Induction Generator, SEIG）除具有异步发电机成本低、可靠性高、易维护等诸多优点外，还独具短路自保护等更可靠的优点，应用日益广泛，尤其在绿色小水电、小风电等节能环保新能源微电网建设方面，日益受到人们的高度关注[2]。
随着对SEIG的理论研究逐步深入，其应用技术发展更加快速，自身电压和频率调节能力的不足也逐步得以克服[3-8]。然而考虑到控制实现、节能和相关设备成本等诸多因素，理论方面的更深研究仍显得异常重要。其理论分析方法主要归结为两种类型：其一为基于稳态数学模型，该方法在早期研究中用得较多[9-11]，通常采用数值计算，励磁电容临界值的计算过程较简易，但计算的程序实现不可避免地存在效率和发散性问题，而且无法评价暂态性能；其二是基于两相正交参考坐标系下的状态空间暂态数学模型，此方法物理意义较显明，既可计算励磁电容和转子转速的临界值，还可分析定子频率和状态参数的动态响应，因其初期[12-15]以及近期包括求解励磁电容值的Routh判据的方法[16]为直接计算6阶或以上的复杂参数方程，也常采用数值计算，效率和通用性还可提高。
基于SEIG暂态数学模型，用扩展Hurwitz 判据方法可将6阶的原状态空间方程等效地降低为3阶[17-18]，解析计算出带不同性质负载情况下转子转速的临界值[19]和自励产生的必要条件，还是不能对励磁电容临界值进行解析计算。为此，提出一种理论分析方法[20-21]，但因其仍是直接对复杂的6阶参数方程计算，且只能解析计算空载建压电容临界值和带载建压转子转速临界值以及自励产生的必要条件[22]，而仍不能解析计算带载建压电容值。扩展Hurwitz判据方法降低了参数方程阶次，大幅简化了计算，但运算过程有待优化，机理分析亦需深入，以使理论分析更具通用性。
本文建立SEIG在静止两相正交参考坐标系下的空间矢量暂态等效电路及其数学模型，并由此出发，提出一种在系统运动稳定意义上的等价转换分析方法，继而通过暂态稳定性分析得到，临界条件即准极限环的运动形态及其数学表示。对准极限环临界条件解析计算，得到给定转子转速和电阻情况下的励磁电容和定子频率临界值的解析解和使发电机能够工作的前提条件，即电阻和励磁电容的限值及其容许范围。经与其他方法和模型仿真的过程和结果比较，验证了本方法的正确性和有效性，深化SEIG系统机理性分析，适于其他更复杂系统，表明其通用性，解析式具有工程参考价值。
以笼型异步电机、励磁电容和电阻负载组成的SEIG为研究对象，在任意旋转两相正交参考坐标系中，发电机的励磁电感系数是时不变常数，而且只表现为励磁电流的非线性函数[23]。
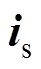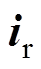图1所示为静止参考坐标系下SEIG空间矢量等效电路。图中，p为微分算子；各空间矢量正方向参照异步电动机，和分别为定、转子电流矢量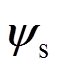；和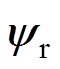分别为定、转子磁链矢量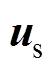；定子端电压矢量；各物理参数均表示为折算到定子侧的实际值，Rs和Rr分别为定、转子侧绕组电阻；Lls和Llr分别为定、转子侧绕组漏电感；M为定、转子绕组间的互感，即励磁电感，且定、转子绕组自感分别为Ls=M +Lls、Lr=M +Llr；C为励磁电容；Rl为电阻负载；w 为转子转速，且保持不变。因M为励磁电流的非线性函数，该等效电路为非线性电路。
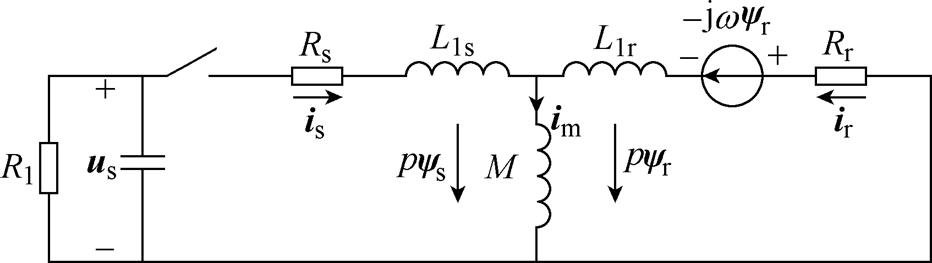
图1 静止参考坐标系下的SEIG空间矢量等效电路
Fig.1 Space-vector equivalent circuit of SEIG in the stationary reference frame
为便于分析SEIG空间矢量模型，做如下假定：①不计电机的铁损；②不计频率和温度变化对绕组电阻的影响；③只考虑气隙磁动势的空间基波分量和电动势、电流的时间基波分量。
由静止参考坐标系下的空间矢量等效电路可知，运行暂态励磁电流Im的计算公式为
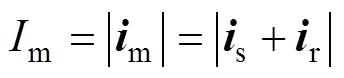（1）定、转子磁链矢量的方程分别为
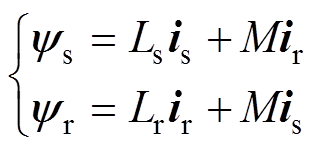（2）
转子旋转产生的运动电动势矢量为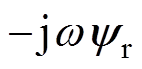
，则笼型异步发电机空间矢量数学模型为
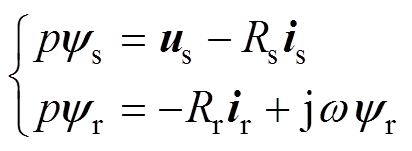（3）定子端的负载与励磁电容并联，空间矢量方程为
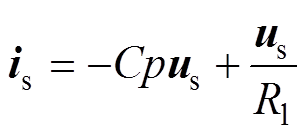（4）
联立方程式（1）～式（4）可得，在静止两相正交参考坐标系下的SEIG空间矢量数学模型为
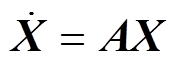（5）式中，X=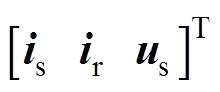
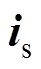，=isa+jisb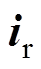；=ira+jirb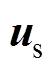；=usa+jusb；漏磁系数s =1-M2/(LrLs)；空间矢量模型的复系数矩阵为
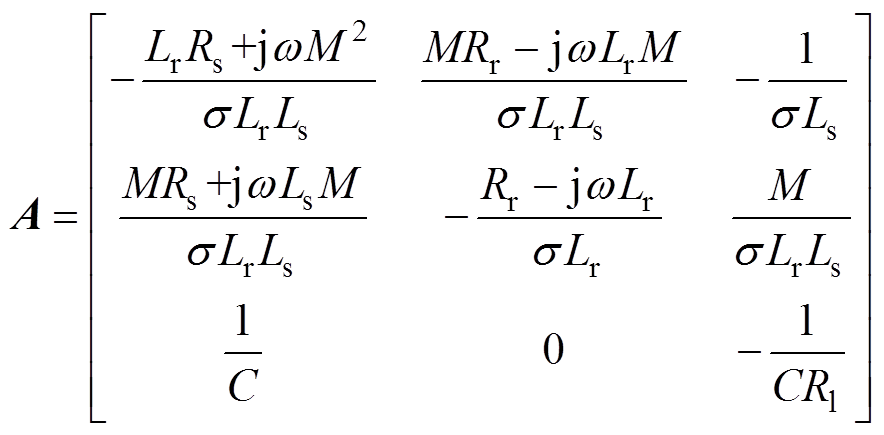
在SEIG系统自励建压或投切负载等暂态变化过程中，各参量发生着剧烈变化，根据式（1）可知，Im变化剧烈。由于在任意旋转两相正交参考坐标系下的励磁电感M都是励磁电流Im的一个确定的非线性函数，该函数是由电机空载磁化特性曲线决定的。用励磁电感关于励磁电流的非线性函数一般形式表示的电机空载磁化特性曲线包括三段：从励磁电流为零时开始的励磁电感单调增大段、中区间的励磁电感基本不变段和励磁电流使磁路饱和时开始的励磁电感单调减小段。而实际上，一般形式的特性曲线单调增大段的励磁电流很小、区间很窄，特别是做发电运行时，在该区段是不可能稳定工作的，稍有扰动就会停止发电，因此该段通常忽略不计，将磁化特性曲线近似为两段，在励磁电流较小时的磁路非饱和区间内，励磁电感近似为基本不变的 常数。
本文采用的电机空载磁化特性曲线近似形式如图2所示，当Im较小时，电机运行在其空载磁化特性曲线的非饱和区，M基本不变，此时电机基本工作在电动机状态，可视其为线性系统；当Im一旦大于某值，电机运行则进入空载磁化特性曲线的饱和区，随之开始进入发电运行模式，M也将随Im的增大而非线性地单调减小，该空间矢量数学模型则表现为非线性特征。
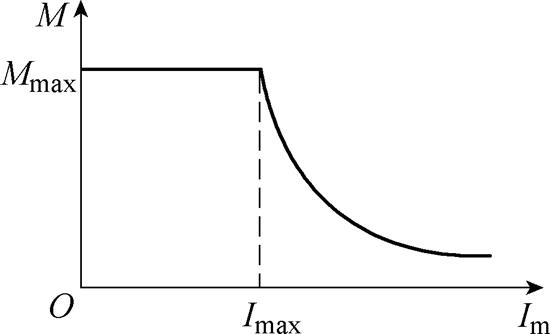
图2 SEIG空载近似磁化特性曲线
Fig.2 Approximate magnetization curve of unloaded SEIGs
基于SEIG状态空间暂态数学模型，系数矩阵为实数，通过对系统能量转化和运动性质的分析，可以明显地得出实系数矩阵特征根在复平面上的基本分布情况。但要确定地解析求解出所有特征根，却因实系数矩阵特征方程阶次较高而难以做到。对于同一个系统，采用同一参照系下的不同表示方式，虽可能有不同的行为表现或运动形态，但运动性质都必定相同。因此，在同一静止两相正交参考坐标系下，稳定的SEIG系统不管用哪一种数学模型描述分析都是稳定，而不稳定的就都不稳定，与采用的数学模型无关。其实，实系数矩阵表示的状态空间数学模型与复系数矩阵表示的空间矢量数学模型是具有紧密关联的，为此，引入一项定义和一条定理。
对于任意复方阵方程
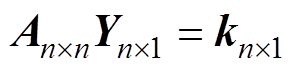（6）利用矩阵的方块形式，可写成
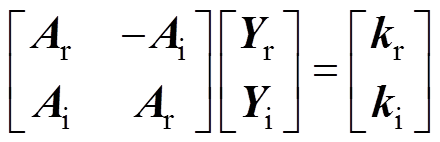（7）
式中，Ar、Yr、kr和Ai、Yi、ki分别表示矩阵A、Y、k对应的实部和虚部实矩阵。经此变换，把一个n´n的复系数矩阵方程转变为一个2n´2n的实系数状态空间方程，方程阶次增大了一倍，运算复杂度也大幅增加，甚至难以解析计算。将这种运算变换的性质应用于SEIG系统参数的解析求解问题。
定义 按n´n排列的复数方阵A到按2n´2n排列的实数方阵Q的映射F：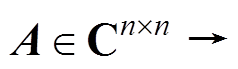
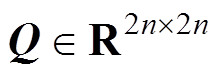，若
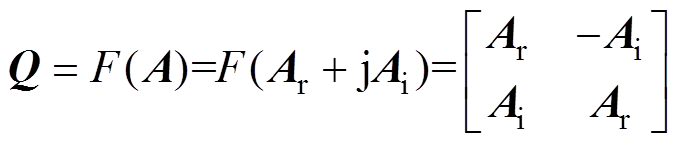（8）定理 可对角化复数方阵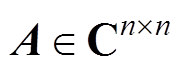
在映射F作用下的象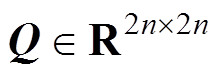的特征值为A的特征值及其共轭。
证明：设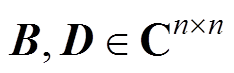
，依“定义”，对二者乘积B·D取F映射，可得
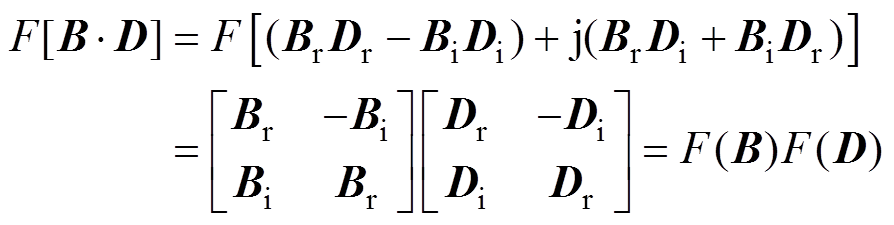（9）式中，Br、Bi和Dr、Di分别为B和D的实、虚部实矩阵。总存在非奇异矩阵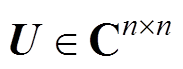
，能使A对角化为相似对角矩阵S，即
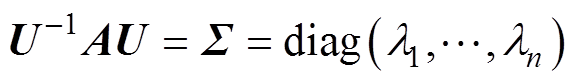（10）
则有
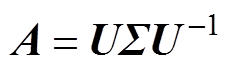（11）根据式（9）性质，并对两边同时取行列式，可得
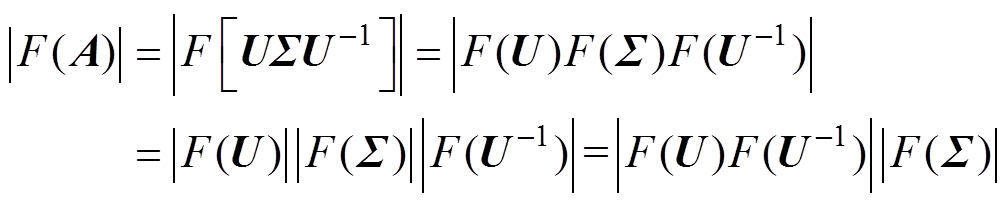
（12）根据“定义”，易知
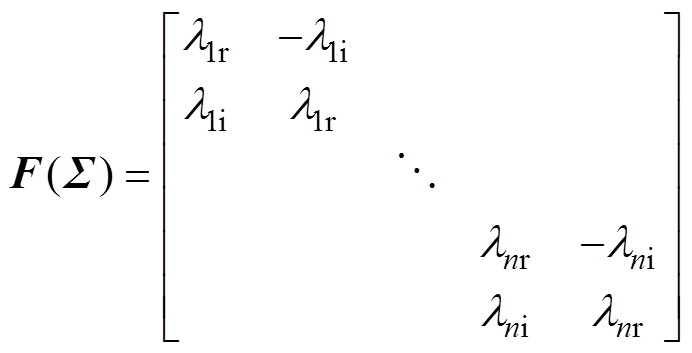（13）
复方阵A和对应实方阵Q的特征多项式分别为
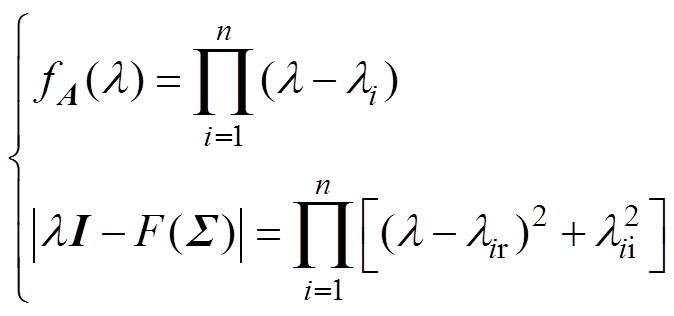（14）式中，li=lir+jlii。当li为实数时，lii=0，且li=lir，Q有实特征值lir二重；当li为虚数时，Q有一对共轭复数特征值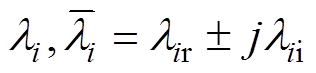
。得证。
由“定理”可知，同一静止两相正交参考坐标系下，SEIG的空间矢量数学模型的复系数矩阵和对应状态空间数学模型的实系数矩阵的特征根在复平面上具有相同分布，都包含了系统稳定性的全部信息，即两种方法在判定系统稳定性问题上是等价的。那么，“定理”可用作系统暂态稳定性的重要判定依据；反之，由系统整体的运动性质亦可确定对应的复、实系数矩阵的特征根分布。
尽管两种数学模型在对系统暂态稳定性的判定上等价，但系统的运动形态描述却不相同，这依赖于数学模型列向量的物理意义。空间矢量模型的列向量分量是状态参数的空间矢量，而状态空间模型的列向量分量则是空间矢量在两相正交坐标轴上的投影，因而同是描述系统运动，形态表现就不同。
不管是用两种模型中的哪一种来分析，在系统稳定与否的性质判定上都是一致的，因此与基于状态空间数学模型进行的稳定性分析相似，带载自励建压需两个必要条件：①为X0≠0；②由于复矩阵A有det(A)≠0，则须$Re(l)≥0，l 为A的特征根。那么要确保自励建压过程持续至成功，暂态运行点X运动能量必须不得衰减，直至达到系统能量和运动的一种平衡状态，区别于基于状态空间数学模型分析的极限环运动，称基于空间矢量数学模型分析的这种运动形态为准极限环。
同理，对于投切负载的暂态过程，即初始条件为非原点微小邻域内的任意能量组配的运动平衡状态-某种准极限环运动，当受到某种扰动时，不管暂态运动过程多么复杂，最终都会过渡到另一种能量重组的运动平衡状态，当然系统崩溃回到原点除外。因此，基于空间矢量模型的理论分析可以可靠地判定系统的稳定性及其平衡状态。
基于空间矢量数学模型的稳定性分析得到的能量平衡是一种临界条件，等同于基于状态空间数学模型的稳定性分析结果，但运动形态不同，则称该临界条件为准极限环条件。其数学描述为：系统空间矢量数学模型的复系数矩阵A的特征方程式（15）与虚轴有公共点jws或-jws。
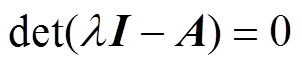（15）不妨设公共点为jws（ws＞0），依据准极限环条件，有det(jwsI-A)=0，由实、虚部分别等于0得
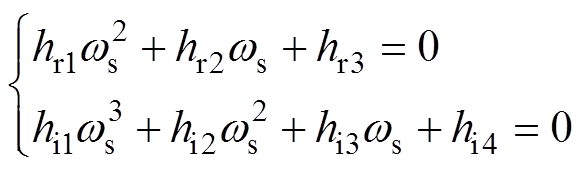（16）其中
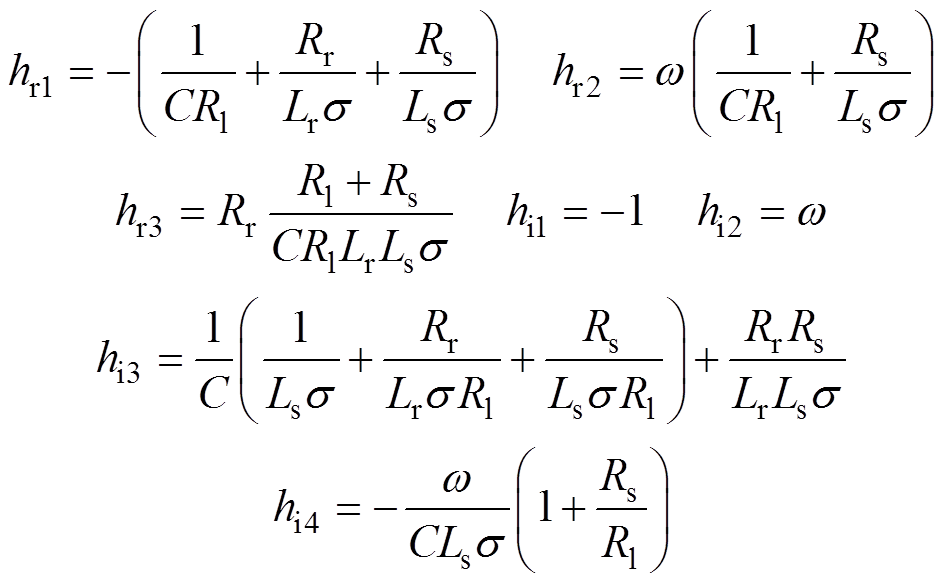
由式（16）之第一式即实部等于0的方程可知，其既是关于定子频率ws的一元二次方程，同时又是分别关于励磁电容的倒数1/C和转子转速w 的一元一次方程。因此，依其既可得到在给定转子转速和负载条件下的励磁电容和定子频率的值，也可得到在给定励磁电容和负载条件下的转子转速和定子频率的值，定子频率值表征的是SEIG稳态运行准极限环运动形态的特征量。
当转子转速w 和负载Rl为已知时，首先由实部等于0的方程解出C，它是关于定子频率ws、转子转速w 和负载Rl的函数，即
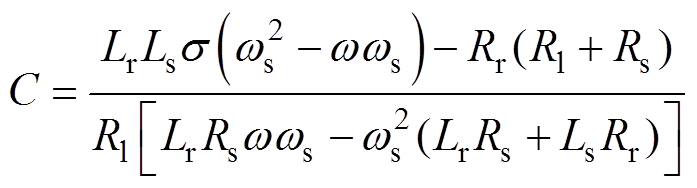（17）然后将其代入式（16）的第二式即虚部等于0的方程，经化简和整理，可得
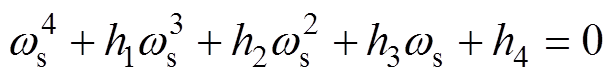（18）
其中
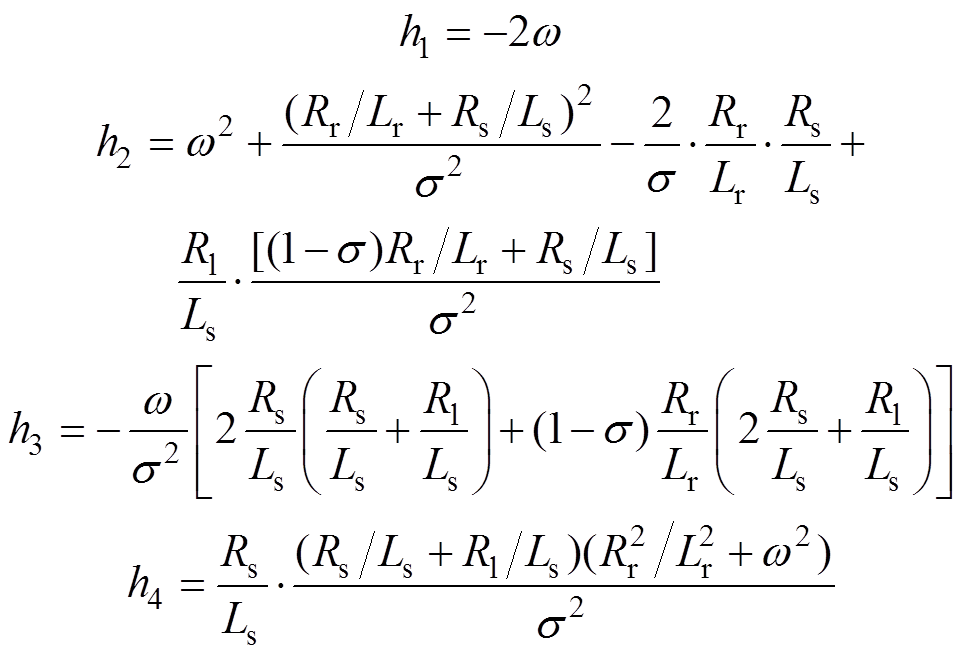
式（18）是一个关于ws的一元四次参数方程，经等效变换，易得其解析解，由于定子频率ws须为实数，经其中两判别式D1≥0且D2≥0得到，只有其中的两个解符合条件，它们分别为
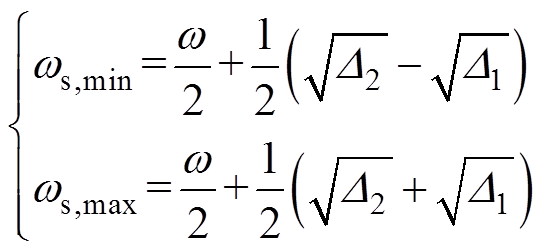（19）
其中
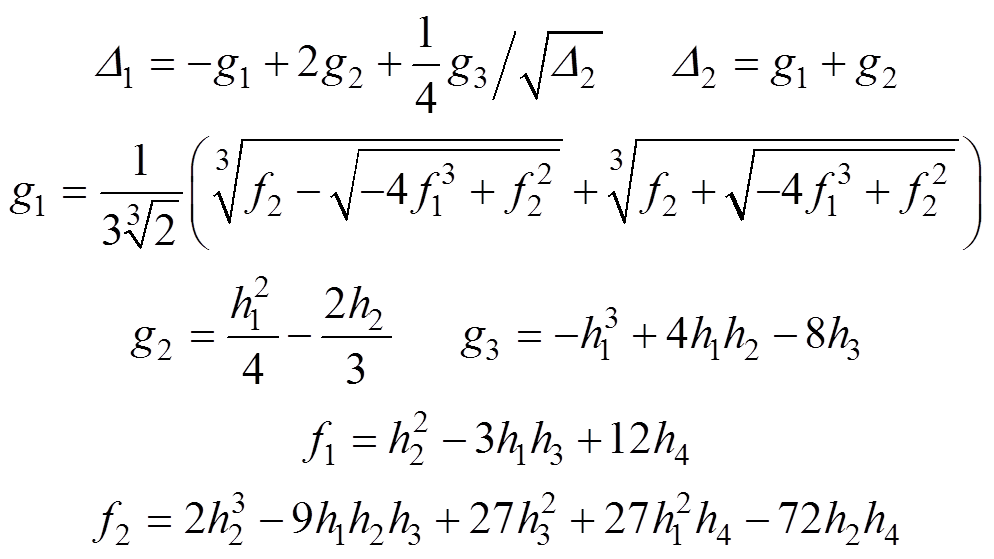
将定子频率解析式（19）代入式（17）即可得到给定转子转速和电阻情况下的励磁电容临界值解析解为
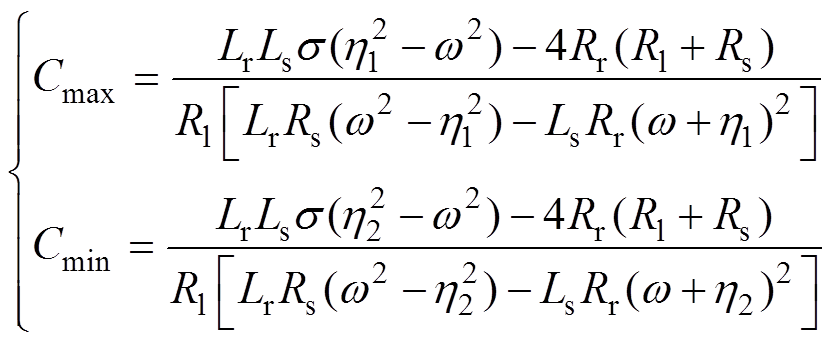（20）
式中，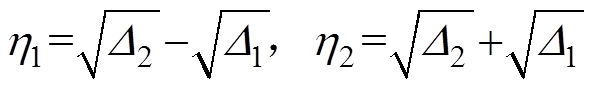
。
由于SEIG是发电运行模式，定子频率ws必定小于转子转速w，且大小相差应不太大，则励磁电容C关于ws的函数式（17）是一个单调递减函数，则ws为最大值ws,max时，C取得最小值；反之，ws为最小值ws,min时，C取得最大值，由此还可确定实际工作条件的解析式。
综上，在给定转速和负载条件下，确保自励建压成功的励磁电容C的取值范围为（Cmin, Cmax）。
由式（16）可知，两方程都是关于转子转速w 的一次参数方程，不妨先假设励磁电容C和电阻Rl为已知，首先由实部等于0的方程解出w，它是关于定子频率ws、励磁电容C和电阻Rl的函数。
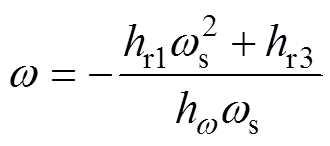（21）式中，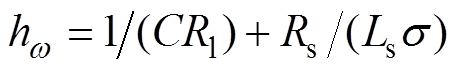
表示hr2中w 的系数，将式（21）代入虚部等于0的另一方程可得，关于定子频率二次方
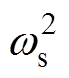的二次参数方程为
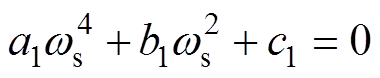（22）其中
求解式（22）可得，给定励磁电容和负载情况下临界条件的定子频率ws解析解式为
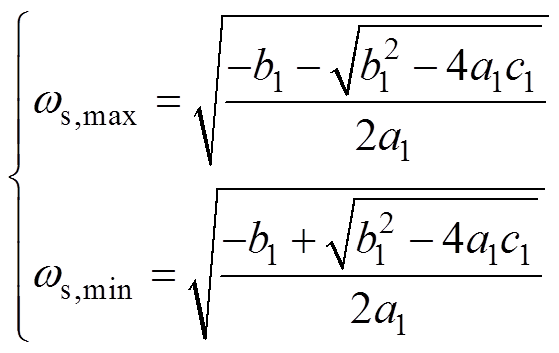（23）将定子频率解析式（23）代入式（21）即得，给定励磁电容和负载电阻情况下转子转速临界条件解析解为
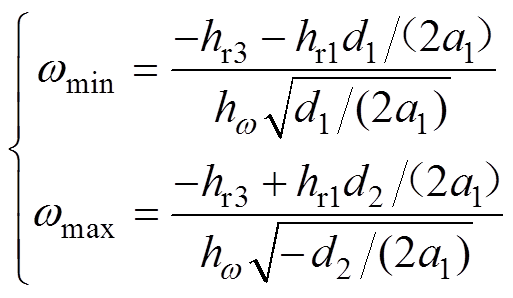（24）
其中
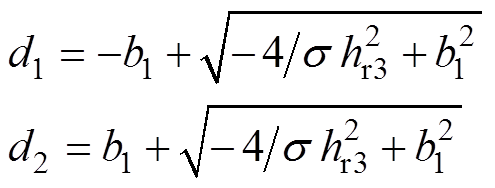
由于hr1＜0，hr3＞0且hw＞0同时成立，则式（21）是关于定子频率ws的一个单调递增函数，则ws为最大值ws,max时，w 取得最大值；反之，ws为最小值ws,min时，w 也取得最小值，由此还可进一步确定实际工作条件的ws和w 解析式。
由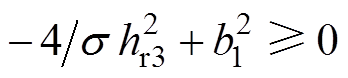
可得，等价整理化简为
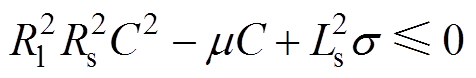（25）式中，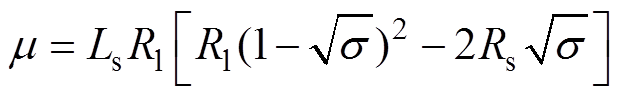
。由此可知，它是一个关于C的二次参数不等式，当且仅当其判别式大于等于0时，不等式的解集为非空集，物理意义为发电机能够工作，解其判别式得
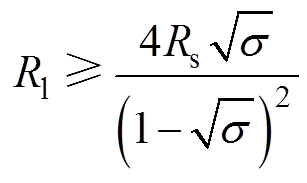（26）该式表明，SEIG带载自励建压须Rl大于一定值，其大小仅由异步发电机系统本身的参数决定。
当负载满足式（26）情况下，解不等式（25）可得，励磁电容容许限值的解析式为
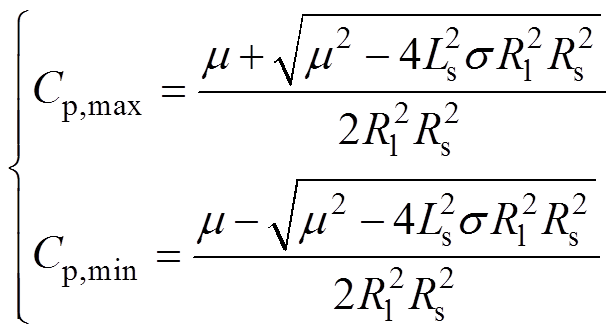（27）则励磁电容容许取值的范围为（Cp,min, Cp,max）。
需要强调指出的是，两种条件下的励磁电容值解析式的实际物理意义根本不同，主要体现在：①前者指的是运动稳定临界条件的励磁电容值，亦即使SEIG能量平衡能够稳态运行的励磁电容值，反映正常工作实际成立的充分条件，而后者则是一种理论上的分析值，反映的则是能够实际工作的前提或必要条件；②前者对于确定的稳态其励磁电容和定子频率的值都是唯一的，因此有一组多余，可舍去，后者限于实际工作条件，转速不可能太高，则励磁电容值不宜太小，而励磁电容值也不可能太大，故可用于自励建压尤其是投切负载暂态过程分析的取值参考。
为便于验证由空间矢量数学模型得到的准极限环条件及励磁电容临界值和限值解析计算式的正确性，本文首先与由状态空间数学模型得到的极限环条件及励磁电容限值解析计算式和稳态条件及稳态励磁电容值[22]作比较，其次为更贴近发电机工作实际，将由本文解析式计算所得额定条件励磁电容值代入仿真模型，检验能否建压成功。所用发电机数据：磁极对数nP=2，额定功率PN=2.2kW，额定电压UN=380V（星形联结），额定电流IN=5A，额定频率fs=50Hz，作发电机运行时，额定转速nN=1 430r/min。电机自身参数为：定子电阻Rs=3.383W；转子电阻Rr=2.973W；定子漏感Lls=8.479mH；转子漏感Llr= 8.479mH；非饱和区励磁电感M=0.287 5H。
由式（26）可判断，与之前文献[21-22]所得计算结果完全一致。当给定w =223.17rad/s，Rl=29.49W，M=0.287 5H时，两种方法对自励建压励磁电容临界值和限值所得计算结果见表1。由表1可知，对自励建压励磁电容临界值中的最小值的计算两种方法的结果（或饱和区稳态所需值）一致；励磁电容限值计算结果完全一致。
表1 自励建压励磁电容临界值和限值的计算结果
Tab.1 Computed results of critical values and limit values of exciting capacitance for self-excitation buildup
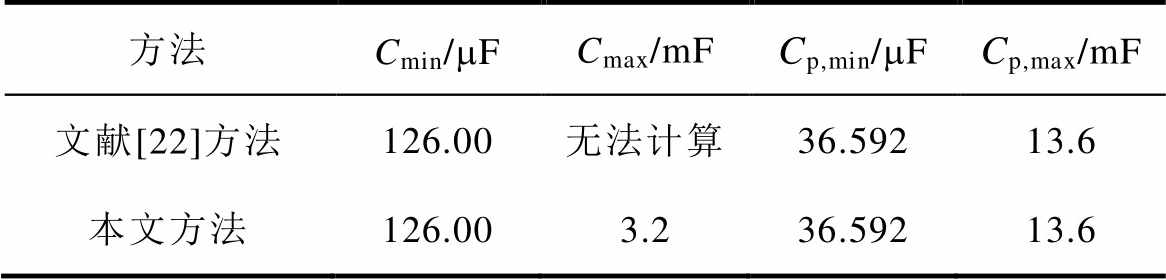
方法Cmin/mFCmax/mFCp,min/mFCp,max/mF 文献[22]方法126.00无法计算36.59213.6 本文方法126.003.236.59213.6
进一步地，该异步发电机额定工作条件的转子转速w =299.5rad/s、负载电阻Rl=22W，带载建压开始时励磁电感M =0.287 5H，则由式（20）可解得Cmax=1.748mF，Cmin=106.79mF，显然最大值因使磁路深度过饱和而不可能工作，因而实际能够工作的励磁电容理论值为Cmin=106.79mF。考虑到模型误差影响和响应时间，配置所需励磁电容为C=108mF，图3所示为SEIG带载建压的定子a相电压仿真波形，显示带载建压达到稳态的持续时间约为42.4s，说明越接近励磁电容理论临界值，带载建压响应速度越慢，以至不能成功自励建压，亦即不能发电，仿真数据与本文理论分析结果基本一致。
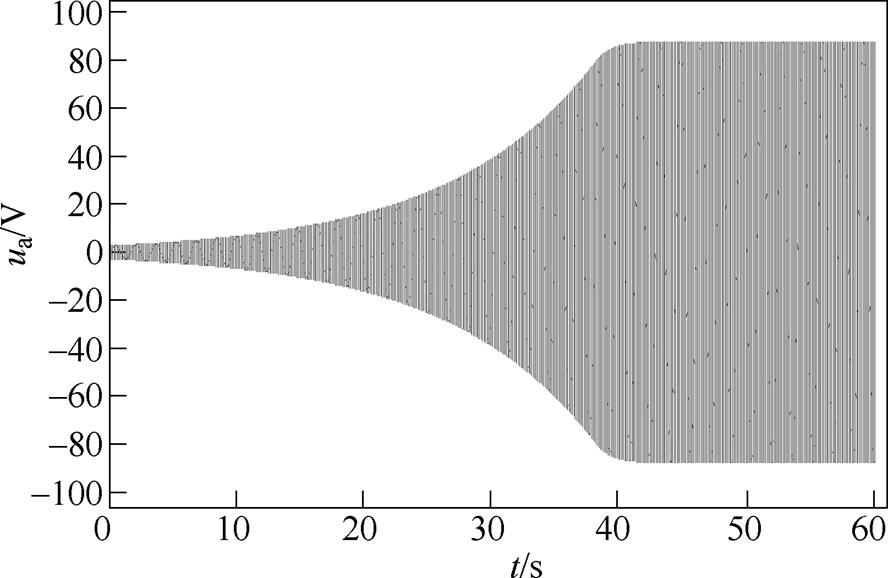
图3 w =299.5rad/s、Rl=22W、C=108mF的 SEIG带载建压a相电压仿真波形
Fig.3 a-phase voltage simulation waveform of loaded buildup for w =299.5rad/s、Rl=22W、C=108mF of SEIG
综合以上一般情况下的两个方面比较，表明本文理论分析方法及其所得励磁电容解析计算公式的正确性、高效性和通用性。
为证明本文方法和解析计算式更具一般性，选择一种不同电机[15]进行测试，并与不同计算方法进行比较。额定值：PN=2.2kW，UN=380V（星形联结），IN=5A，nP=2；作发电机单独运行时，nN=1 500r/min。电机参数：Lls=Llr=0.010 9H，Rs=2.8W，Rr=3.2W，互感不饱和值M=0.375 4H。
为深入验证本文方法及其所得励磁电容和转子转速临界值解析计算式的正确性，特别是与基于状态空间数学模型的方法及其所得空载自励建压励磁电容和转子转速临界值解析计算式[20]进行比较，对同一算例用不同计算方法所得计算结果对比见表2。数据显示，四种算法对励磁电容临界值的计算结果一致；解析式法和一维优化算法能计算转速且结果一致，基于稳态模型的数值法（文献[10]）则不能；特别是后面两种解析式方法计算结果基本一样。
表2 空载（Rl=¥）自励建压临界值计算结果
Tab.2 Computed results of critical values for unloaded (Rl=¥) self-excitation buildup
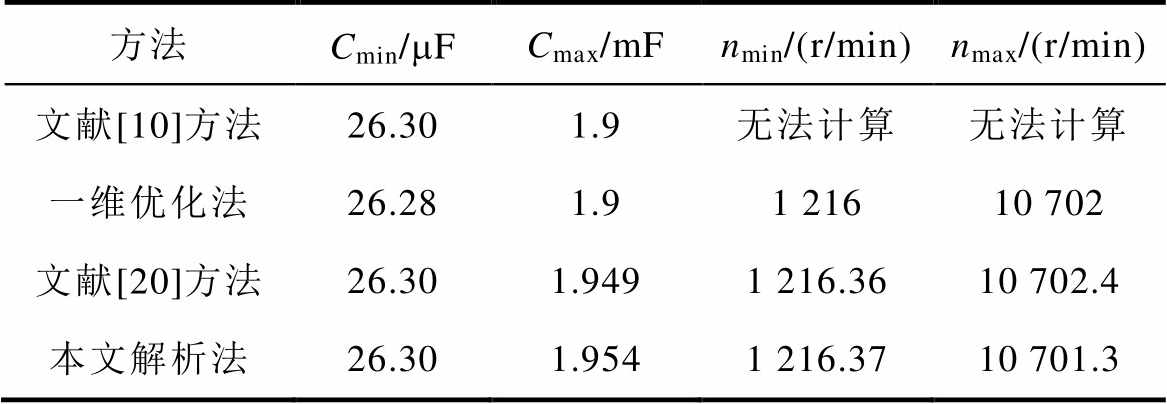
方法Cmin/mFCmax/mFnmin/(r/min)nmax/(r/min) 文献[10]方法26.301.9无法计算无法计算 一维优化法26.281.91 21610 702 文献[20]方法26.301.9491 216.3610 702.4 本文解析法26.301.9541 216.3710 701.3
通过对空载自励建压励磁电容和转速参数进行计算的三种方法对比，基于稳态模型的数值计算方法顾名思义仅仅适用于稳态，同样需要面对求解多元6次参数方程的难题，尽管赋值程序化运算大为方便，但并没有实质解决计算效率的问题；基于暂态模型的一维优化算法虽然可以更为全面反映系统暂态和稳态，但仍囿于对多元6次甚或以上的更复杂参数方程采用的优化等数值算法而没能彻底解决计算效率的问题；第三种方法虽也基于暂态模型可同时研究暂态和稳态响应，并解决了计算效率问题，但仍是对6次的参数方程进行解析计算，过程欠优化，且解析公式仅适用于空载建压的情形，不够全面，故通用性还有一定局限。
与计算SEIG参数临界值的之前方法相比，本文方法是基于静止两相正交参考坐标系上空间矢量的暂态等效电路及其数学模型，不但解析求解出带电阻条件下的转子转速临界值，而且还解析求解出励磁电容临界值，而空载临界值的计算则可视为其Rl=¥时的一种特例。本文分析方法可推广应用到带阻感负载的SEIG临界值的解析计算甚至其他更复杂的系统，深化其运行机理研究，因此具有一定的通用性，解析公式具有较强的工程参考价值，可用于发电机优化高效的配置和性能评估。
针对自励异步发电机带载建压励磁电容值还未能解析计算的问题，本文首先建立了自励异步发电机在静止两相正交参考坐标系下的空间矢量暂态等效电路及其数学模型。由此出发，提出了一种系统稳定性的等价转换分析方法和表征系统能量平衡与运动稳定的准极限环临界条件，该方法有效降低了参数方程的阶次，大幅减少了计算复杂度，从而使解析计算成为可能。通过对临界条件的解析计算，先后解出了给定转子转速和电阻情况下定子频率和励磁电容的临界值解析式，给定励磁电容和电阻情况下定子频率和转子转速的临界值计算式，以及使SEIG能够工作的前提条件：电阻和励磁电容限值解析式及其容许取值范围。最后，与以往其他算法和模型仿真进行了较为全面的比较，计算结果一致，证明了正确性；解析计算公式证明了高效性；特别地对带载建压励磁电容实现了解析计算，证明了方法更具通用性，总之表明了本文所提方法的正确性和有效性，可推广应用到更复杂系统。
参考文献
[1] Chauhan Y K, Jain S K, Singh B. A prospective on voltage regulation of self-excited induction gener- ators for industry applications[J]. IEEE Transactions on Industry Applications, 2010, 46(2): 720-730.
[2] Singh G K. Self-excited induction generator for renewable applications[J]. Encyclopedia of Sustai- nable Technologies, 2017: 239-256.
[3] Rajagopal V, Singh B, Kasal G K. Electronic load controller with power quality improvement of isolated induction generator for small hydro power generation[J]. IET Renewable Power Generation, 2011, 5(2): 202-213.
[4] Chilipi R R, Singh B, Murthy S S, et al. Design and implementation of dynamic electronic load controller for three-phase self-excited induction generator in remote small-hydro power generation[J]. IET Rene- wable Power Generation, 2014, 8(3): 269-280.
[5] Singh B, Murthy S S, Chilipi R R, et al. Static synchronous compensator variable-frequency drive for voltage and frequency control of small-hydro driven self-excited induction generators system[J]. IET Generation Transmission & Distribution, 2014, 8(9): 1528-1538.
[6] Chilipi R R, Singh B, Murthy S S. Performance of a self-excited induction generator with DSTATCOM- DTC drive-based voltage and frequency controller[J]. IEEE Transactions on Energy Conversion, 2014, 29(3): 545-557.
[7] Scherer L G, Tambara R V, Camargo R F. Voltage and frequency regulation of standalone self-excited induction generator for micro-hydro power gener- ation using discrete-time adaptive control[J]. IET Renewable Power Generation, 2016, 10(4): 531-540.
[8] Tischer C B, Tibola J R, Scherer L G, et al. Proportional-resonant control applied on voltage regulation of standalone SEIG for micro-hydro power generation[J]. IET Renewable Power Generation, 2017, 11(5): 593-602.
[9] Tandon A K, Murthy S S, Berg G J. Steady state analysis of capacitor self-excited induction gener- ators[J]. IEEE Transactions on Power Apparatus and System, 1984, 103(3): 612-618.
[10] Chan T F. Capacitance requirements of self-excited induction generators[J]. IEEE Transactions on Energy Conversion, 1993, 8(2): 304-311.
[11] 吴新振, 王祥珩. 异步发电机空载建压电容值的确定方法[J]. 清华大学学报, 2004, 44(7): 893-896.
Wu Xinzhen, Wang Xiangheng. Self-excited capa- citance or induction generator for no load oper- ation[J]. Journal of Tsinghua University, 2004, 44(7): 893-896.
[12] Harrington R J, Bassiouny F M M. New approach to determine the critical capacitance for self-excited induction generators[J]. IEEE Transactions on Energy Conversion, 1998, 13(3): 244-249.
[13] Wang Li, Su Jianyi. Dynamic performance of an isolated self-excited induction generator under various loading conditions[J]. IEEE Transactions on Energy Conversion, 1999, 14(1): 93-100.
[14] 郝宽胜, 吴新振. 基于暂态模型的异步发电机稳压电容计算[J]. 中国电机工程学报, 2007, 27(3): 51-56.
Hao Kuansheng, Wu Xinzhen. Capacitance calcu- lation for keeping constant voltage of induction generators based on transient model[J]. Proceedings of the CSEE, 2007, 27(3): 51-56.
[15] 吴新振, 郝宽胜, 兰勇. 以特征值为判据的异步发电机自激建压过程分析[J]. 中国电机工程学报, 2008, 28(8): 111-116.
Wu Xinzhen, Hao Kuansheng, Lan Yong. Analysis of voltage build-up for self-excited induction generator based on eigenvalues[J]. Proceedings of the CSEE, 2008, 28(8): 111-116.
[16] 李嘉, 吴新振, 王海峰. 基于Routh判据的自激感应发电机空载建压分析[J]. 电工技术学报, 2018, 33(7): 1523-1530.
Li Jia, Wu Xinzhen, Wang Haifeng. Analysis of no-load voltage build-up for self-excited induction generator based on routh criterion[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1523-1530.
[17] Bodson M, Kiselychnyk O. The complex Hurwitz test for the analysis of spontaneous self-excitation in induction generators[J]. IEEE Transactions on Auto- matic Control, 2013, 58(2): 449-454.
[18] Bodson M, Kiselychnyk O. Analysis of triggered self-excitation in induction generators and experi- mental validation[J]. IEEE Transactions on Energy Conversion, 2012, 27(2): 238-249.
[19] 李嘉, 吴新振, 王海峰. 基于Hurwitz判据的自激感应发电机带载建压分析[J]. 中国电机工程学报, 2018, 38(10): 3094-3101.
Li Jia, Wu Xinzhen, Wang Haifeng. Voltage build-up analysis of loaded self-excited induction generators based on Hurwitz stability criterion[J]. Proceedings of the CSEE, 2018, 38(10): 3094-3101.
[20] 李海涛, 卢子广. 基于Lyapunov稳定性理论的自励异步发电机建压过程分析[J]. 电工技术学报, 2014, 29(9): 167-173.
Li Haitao, Lu Ziguang. Analysis of voltage build-up for self-excited induction generators based on Lyapunov stability theory[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 167-173.
[21] 李海涛, 卢子广, 杨达亮. 自励异步发电机带载稳态的解析计算[J]. 中国科学: 技术科学, 2014, 44(11): 1202-1210.
Li Haitao, Lu Ziguang, Yang Daliang. Analytic computation for steady states of loaded self-excited induction generators[J]. Scientia Sinica: Techno- logica, 2014, 44(11): 1202-1210.
[22] Li Haitao, Lu Ziguang, Li Zhuo. Transient analysis of load switches of self-excited induction generators based on Lyapunov stability theory[J]. IEEJ Transa- ctions Electrical and Electronic Engineering, 2017, 12(3): 337-346.
[23] Krause P C, Wasynczuk O, Sudhoff S D. Analysis of electric machinery and drive systems[M]. New York: IEEE Press, 2002.
Analytical Calculation of Exciting Capacitance for Buildup of Loaded Self-Excited Induction Generators
Abstract To obtain the capacitance for buildup of loaded self-excited induction generators (SEIGs) analytically, firstly, this paper established the space-vector transient equivalent circuit and the mathematic model in the stationary two-phase orthogonal reference frame. Thereafter, an equivalent transformation analysis approach for system stability was proposed, and the critical condition of quasi-limit cycle representing energy equilibrium and motion stability was obtained. Thirdly, the analytical calculation of the critical condition of quasi-limit cycle is obtained for loaded buildup under a given rotor speed and resistance. It was easier to obtain the critical rotor speeds of loaded buildup under a given capacitance and resistance. Moreover, the necessary conditions for ensuring self- excitation were calculated, i.e. the analytic limit values of the resistance and capacitance. Finally, compared with other methods and model simulations under different operating modes, the proposed approach has good agreement of the calculated results, simplicity of calculation and applicability of analytic formulas, which is applicable to more complex systems. The analytic formulas are helpful for system configuration optimization and performance evaluation.
keywords：Self-excited induction generator (SEIG), transient equivalent circuit, space-vector model, transient stability, analytic formulas
中图分类号：TM343
DOI: 10.19595/j.cnki.1000-6753.tces.190595
李海涛 男，1980年生，博士，讲师，研究方向为异步发电机系统稳定性分析与控制、新能源发电系统等。E-mail: fzhli_sh@163.com（通信作者）
蔡建平 男，1975年生，博士，教授，研究方向为非线性系统控制、鲁棒控制、自适应控制的理论与应用等。E-mail: caijianping2001@163.com
收稿日期 2019-05-20
改稿日期 2019-07-26
国家自然科学基金资助面上项目（61573322）和浙江省水利科技计划项目（RC1815）资助。
（编辑 赵 鹏）