图1 磁性纳米粒子对外部磁场的响应
Fig.1 The response of magnetic nanoparticles to external magnetic fields
摘要 磁性粒子成像是一种具有高成像分辨率的示踪剂成像技术。针对现阶段成像系统的开放式扫描难题，利用高灵敏度的线型零磁场，实现高分辨率的二维扫描成像方法。设计一种具有开放式线圈结构的线型零磁场，利用梯度静磁场构造线型零磁场以确定示踪剂的位置，在均匀交变磁场实现线型零磁场的平移扫描。对该线圈结构进行详细的设计分析，首先确定实现高分辨率的磁性粒子成像线圈系统的电流驱动方式；接着对开放式线型零磁场的扫描方式进行有限元仿真计算分析；最后根据其驱动方式与平移扫描区域范围的关系，进行粒子质量分数模型的成像实验。实验结果表明，开放式线圈结构所构成的线型零磁场在1.316T/m的梯度磁场中，可以实现在成像区域为17mm×17mm内的磁性纳米粒子示踪剂的高分辨率成像，其分辨率可达亚毫米级，理论证明了开放式线型零磁场扫描方式用于磁性粒子成像的可行性。
关键词：磁性粒子成像 开放式 成像分辨率 线型零磁场 有限元仿真
磁性粒子成像（Magnetic Particle Imaging, MPI）是一种新型示踪剂成像技术，利用磁性纳米粒子示踪剂在零磁场中的非线性磁化特性，可视化被测物内的示踪剂质量分数，从而检测磁性纳米粒子示踪剂的空间分布。由于MPI的信号直接来自于可视范围内的示踪剂质量分数，可以获得纳摩尔级检测灵敏度[1]，以及亚毫米级的成像分辨率[2]，因此近年来得到广泛的关注，并应用于细胞跟踪[3]、血管造影[4]以及炎症成像[5]等领域。
MPI由德国科学家Bernhard Gleich和Jürgen Weizenecker教授首次提出，于2005年在《Nature》上发表了一篇文章，成像实验初步证实了MPI成像的可行性[2]。并在2009年首次实现体内MPI扫描，对搏动的小鼠心脏进行三维实时扫描成像[6]。近几年，MPI的相关研究工作取得了飞速发展。飞利浦实验室研究团队提出了一种新的零磁场方案，通过利用线型零磁场（Field-Free Line, FFL）来提高MPI的灵敏度[7]。Lübeck大学的研究团队引入了第一个可行的FFL线圈布置系统，并引入了基于FFL扫描方式的图像重建算法，进一步提高FFL线圈几何的效率[5-11]。日本Kyushu大学的研究团队开发了一种检测3次谐波的高灵敏度线型零磁场MPI系统，检测到在50mm距离处1μg的磁性纳米粒子[12-15]。
但现阶段的MPI系统以封闭式结构居多，封闭式系统虽能产生较稳定且较大的磁场梯度，但限制了成像目标的体积大小，造成测量上的局限性。同时，由于MPI技术是利用磁性纳米粒子在零磁场下的独特响应来进行成像，使用基于系统矩阵的方法进行重建[16]，仅零磁场附近的粒子可以发出特征信号。因此具有高灵敏度和高成像速度的线型零磁场的扫描方式成为首选。同时成像分辨率与零磁场的梯度强度直接相关[1]。因此，利用开放式成像空间结构构造线型零磁场，即对复杂磁场的设计，尤其是零磁场的精细设计对MPI成像具有重要意义。
针对现阶段成像系统的开放式扫描难题，本文设计了一种开放式线圈结构的线型零磁场，通过改进线圈形状及布置结构的方法构建零磁场线圈布置结构，提高零磁场的均匀性，并设计相应的电场驱动方式实现MPI线圈结构的成像区域磁场扫描，控制输入电流的幅度，实现线型零磁场的平移扫描。同时，进行有限元仿真分析研究，确定实现高精度的线型零磁场所需的电流驱动方式，详细分析其磁场分布、磁场均匀性及线型零磁场的分辨率，实现高分辨率的平面二维扫描成像方法。
磁性纳米粒子的非线性磁化特性是MPI成像的基础。磁场强度较大时，磁性纳米粒子出现磁化强度饱和的状态，仅当在零磁场附近时，磁性纳米粒子可以对外加的交变磁场产生响应，即粒子发出特征信号。利用外界的检测线圈可以接收到该粒子信号，通过感应电压表征，提取粒子的频率信号就可进行MPI图像重建。图1所示为磁性纳米粒子对外部磁场的响应。非线性磁化曲线如图1a所示，外加如图1b所示的足够幅值的交变磁场，则磁性纳米粒子将呈现出图1c所示的磁化响应M(t)，这时接收到感应电压信号如图1d所示。
图1 磁性纳米粒子对外部磁场的响应
Fig.1 The response of magnetic nanoparticles to external magnetic fields
如果每一个零磁场区域内的磁性纳米粒子信号都可以被检测到，使用基于系统矩阵的方法进行重建，其中扫描点源已进行校准[15]，就可以得到成像区域内的磁性纳米粒子分布图像，实现磁性粒子的空间成像。
成像分辨率是评估零磁场的重要指标，即为能分辨的两点间的最小距离[17]。MPI的成像分辨率由成像区域内的磁场和所使用的磁性纳米粒子的粒径决定。其中，空间内磁场的梯度压缩零磁场的宽度，较小的零磁场宽度可以使MPI成像达到较高的分辨率；磁性纳米粒子的粒径决定了其在磁场中的非线性磁化范围，从而影响着成像分辨率的大小。综合考虑磁场梯度大小和粒径大小这两点因素，可以使用磁化强度的半峰宽（Full Width at Half Maxima, FWHM）来描述磁化特性的动态范围宽度[18]。在MPI中，粒子磁化的饱和特性可以用Langevin函数来描述，FWHM即为Langevin函数导数衰减到其最大值的50%时的信号宽度。利用如图2所示不同粒径下磁化特性曲线导数[19]，可计算出MPI的图像分辨率。
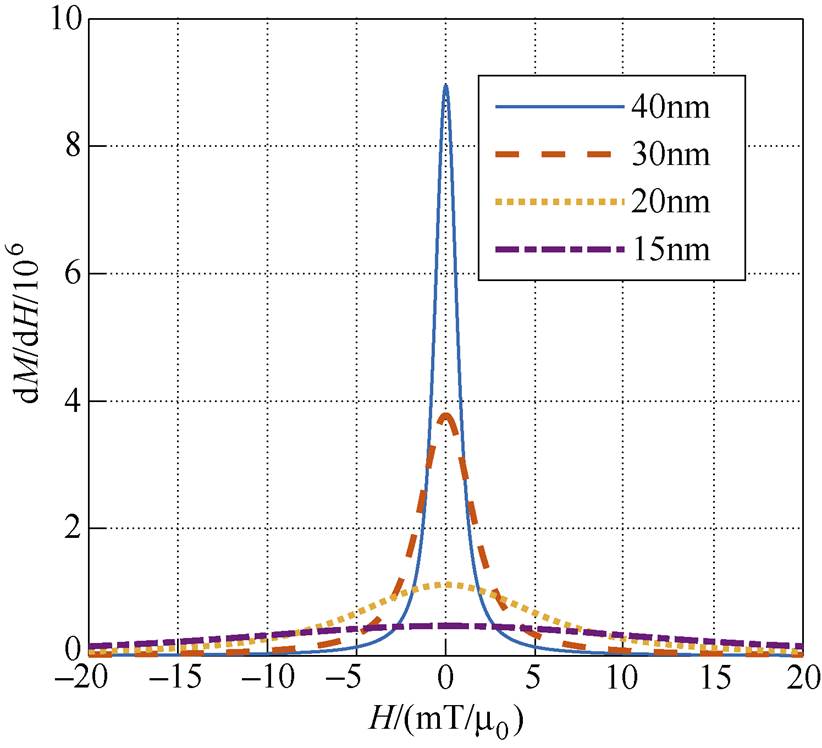
图2 不同粒径下磁化特性曲线导数
Fig.2 Derivatives of magnetization characteristic curves at different particle sizes
若要MPI达到所需要的成像分辨率，就必须要反过来计算得到其相应的磁场梯度大小，并为后面磁场设计提供零磁场的性能需求。用郎之万函数来描述具有超顺磁性的磁性粒子的响应磁场[20]，因此计算其函数的FWHM≈4.16，其与梯度场之间的关系表示为
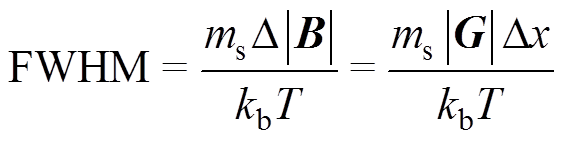（1）
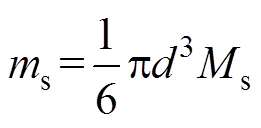（2）
式中，B为磁感应强度；G为磁场梯度；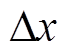
为分辨率；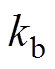
为玻耳兹曼常数；T为热力学温度；
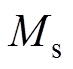为饱和磁化强度（
），
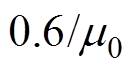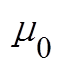为真空磁导率；d为磁性纳米粒子粒径。因此磁场梯度可以表示为
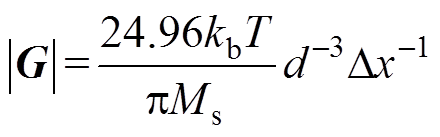（3） 梯度与分辨率和磁性纳米粒子粒径的关系如 图3所示。在相同磁场梯度下，磁性纳米粒子粒径越大，分辨率越高，这是因为粒子的粒径越大，其非线性磁化过程中的动态范围越窄，可产生信号的非饱和区域越小，即单个成像像素点减小，成像分辨率增大。粒子粒径与分辨率之间的关系在式（3）中也可以体现。
图3 梯度与分辨率和粒子粒径的关系
Fig.3 The relationship between gradient and resolution and particle size
从图3中虚线标注处可以看出，使用40nm粒径的磁性纳米粒子时，若要求分辨率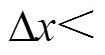
1mm，则磁场梯度
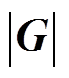＞1.093T/m时，才能满足设计需求。
根据计算所得的磁场梯度，采用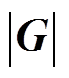＞1T/m为标准设计MPI的零磁场。现阶段零磁场主要分为零磁场点和线型零磁场（FFL），而理论上已经得到证明，基于FFL的MPI的灵敏度是基于FFP的MPI的10倍[9]，且响应粒子的数量比FFP高得多，信噪比（Signal to Noise Ratio, SNR）得到改善，在扫描时间减少的同时提高了成像分辨率。因此本文采用线型零磁场的方式构建MPI所需的零磁场。而MPI布置的几何结构，迄今为止主要有三种：封闭式结构，被测目标置于管状装置的中心；开放式结构，被测目标位于两个扫描系统之间，可从侧面进入；单面线圈结构，用于集成在床、桌子或开发为手持设备[21]。MPI系统需要在其成像面积尽可能的大的前提下，空间分布的磁场保持稳定，因此本文以开放式结构作为系统的几何结构，设计了一种开放式线型零磁场线圈系统。
将已注入磁性纳米粒子的被测目标置于由上、下两侧线圈系统组成的开放式线型零磁场线圈系统中，线圈系统结构如图4所示。被测区域内产生一个线型零磁场区域，利用磁性纳米粒子的非线性磁化响应特性，通过接收线圈获得粒子信号，经过计算机的重建算法来实现磁性粒子在被测目标内质量分数分布的可视化。
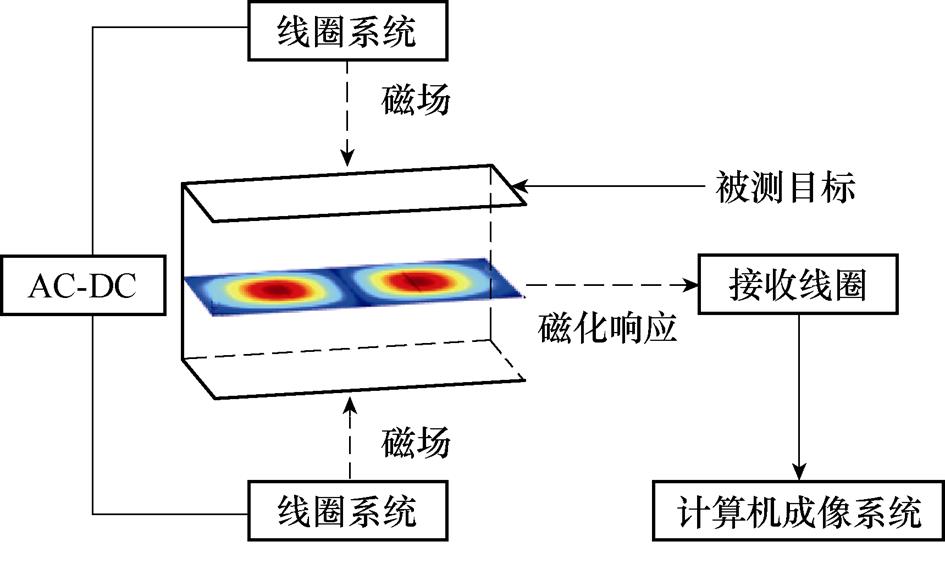
图4 线圈系统结构
Fig.4 Coil system structure
针对开放性结构的线型零磁场构造问题，利用组合线圈设计特殊的线圈布置结构，并采用特定的电流施加方式，构造线型零磁场。根据Biot-Savart公式，计算线圈周围空间磁场[22]。如果两对麦克斯韦线圈的中心轴互相平行，即满足镜像规则，则在此基础上中心轴交点的垂线位置处，始终存在一个FFL[23]。由该原理可以构造出最简单的开放式线型零磁场，其需要通过两对圆线圈产生，这种线圈布置类似于双平面梯度的磁共振成像[24]。
平面梯度线圈布置如图5所示，相邻两线圈紧靠无间距，整个坐标的原点位于系统的中心。在四个线圈中通入直流电流，其中相邻两线圈通入异向电流，同轴两线圈通入同向电流。xz截面以及xy截面的不同线圈形状的线型零磁场均匀性如图6所示，磁场强度矢量在y轴附近（x=z=0）互相抵消，在z=0处的xy平面上产生一段磁场强度为0的区域，该区域即为线型零磁场。
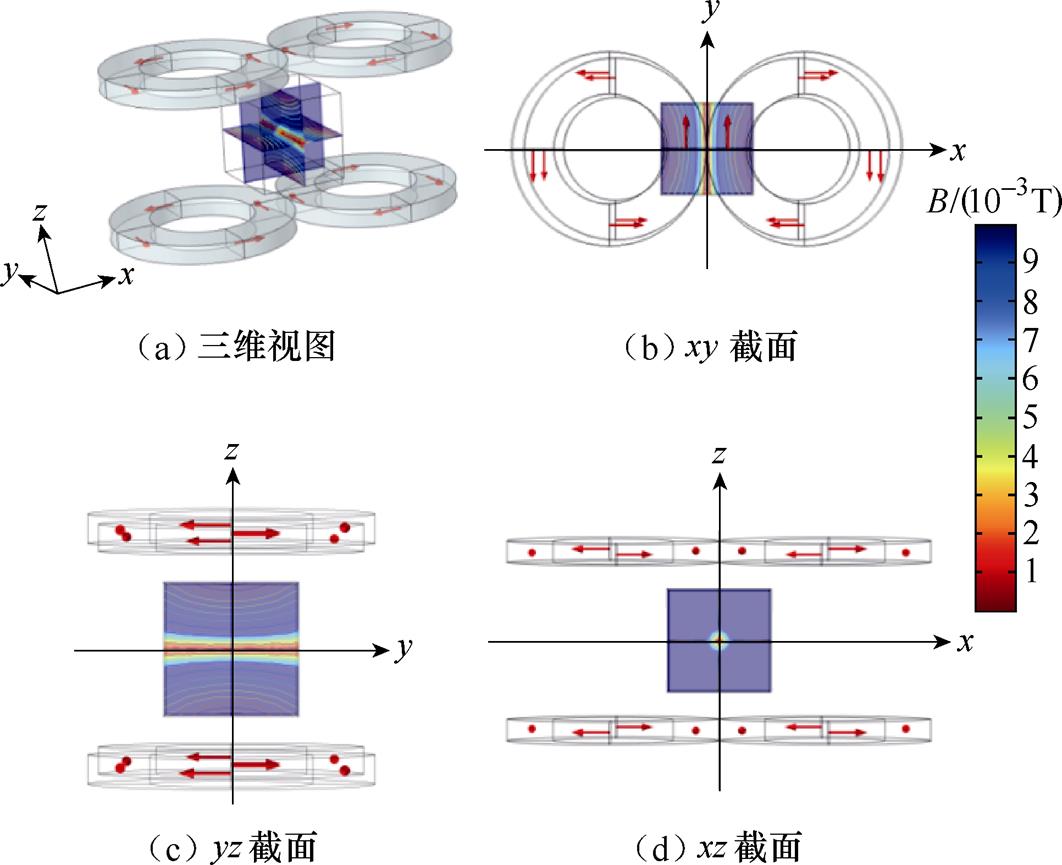
图5 平面梯度线圈布置
Fig.5 Planar gradient coil arrangement
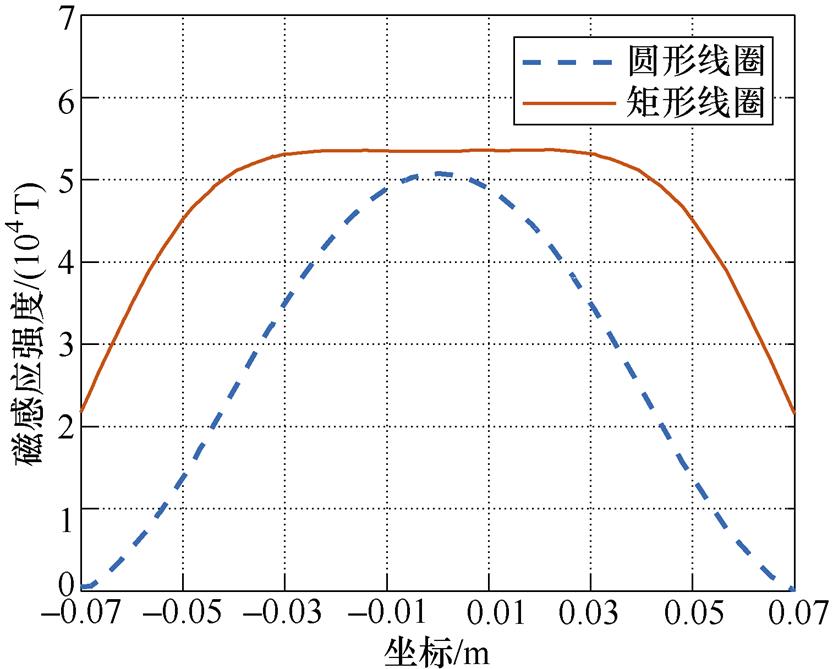
图6 不同线圈形状的线型零磁场均匀性
Fig.6 Magnetic field-free line uniformity of different coil shapes
但从图5c可以明显的看出，线型零磁场的z方向梯度随着与中心点距离的增大而增大，造成了零磁场的不均匀性，这是由于线圈的圆形结构导致的。图6为矩形线圈和圆形线圈沿FFL方向的磁感应强度。其中，在中心点处圆形线圈的磁感应强度最大，并向两侧衰减；而矩形线圈由于其平直的线圈结构，其磁感应强度在中心处保持稳定不变，满足FFL的均匀性需求。因此本文采用矩形线圈来代替原始的圆形线圈[25]，即可消除这一零磁场的非均匀性 问题。
构造出MPI所需的线型零磁场后，若要实现扫描成像，则需要MPI提供成像范围内所有位置的粒子响应信号，因此如何使线型零磁场遍历整个成像区域成为设计磁场的关键。若采用机械移动的扫描方式，即移动线圈结构或移动被测物，不但会给重建图像带来不可预知的伪影，且降低成像速度。因此本文引入电气扫描的方式，对线圈结构进行改进，在提高系统稳定性的同时，实现线型零磁场的扫描。
在原有线圈结构的内侧加入驱动线圈组，在驱动线型零磁场平行移动的同时，提供交变磁场激励。开放式线型零磁场线圈布置结构如图7所示，本文在平面梯度线圈的内部增加一组驱动线圈，两个驱动线圈平行布置在z轴方向上以保持开放式设计，使用一对赫姆霍兹线圈产生均匀磁场。加入驱动线圈后会压缩成像区域的空间，同时线圈组间z方向的间距也会影响成像空间的磁场梯度大小。因此在满足成像区域空间尽可能大的情况下，减小线圈组间距，使其获得满足成像分辨率需求的磁场梯度。为满足上述要求，设置两驱动线圈间距为5cm，且驱动线圈为单匝多层线圈。
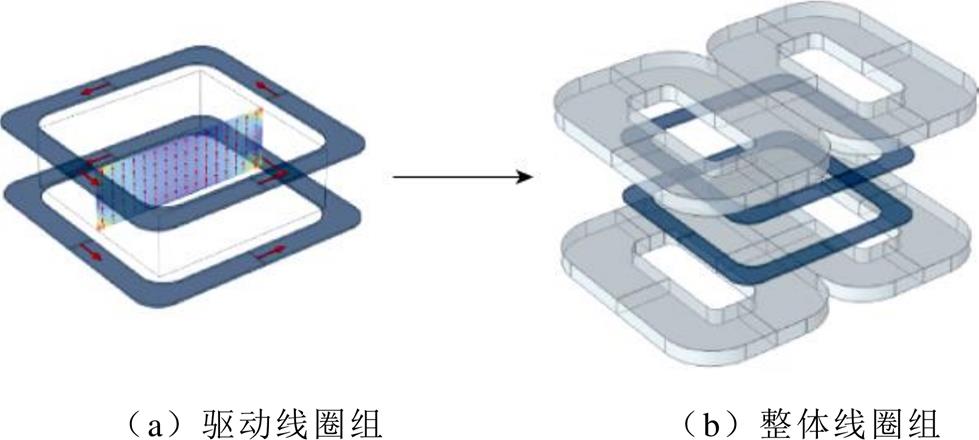
图7 开放式线型零磁场线圈布置结构
Fig.7 Open magnetic field-free line coil arrangement structure
通过这种方法，使用驱动线圈就可以实现FFL在xy平面内水平移动。整体的开放式线型零磁场线圈结构参数见表1。
表1 线圈结构参数表
Tab.1 Coil structure parameter
线圈外尺寸/cm×cm水平厚度/cm垂直厚度/cm匝数 平面梯度线圈18.6×124.61.6184 驱动线圈20×2020.210
为了使线圈在空间中产生磁场，从而构建线型零磁场，所设计的开放式零磁场线圈布置结构中，在线圈中通入电流，线圈内通入的电流会影响线型零磁场周围的磁场梯度，可以反映出零磁场的精度，从而决定成像分辨率。平面梯度线圈产生的磁场是一个梯度静磁场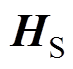
，施加直流电信号，产生线型零磁场，用于选择磁性纳米粒子特征信号的空间位置，其性能与MPI的成像分辨率直接相关。驱动线圈产生的磁场是一个均匀交变磁场
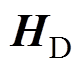，施加低频交流电信号，用于移动线型零磁场及激励施加，其信号峰值决定了扫描范围，且与MPI的成像区域面积直接相关。分别分析平面梯度线圈及驱动线圈内通入电流的大小对磁场梯度的影响，设计合适的电流驱动方式。
静磁场中安培定律的积分和微分形式分别表示为
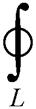
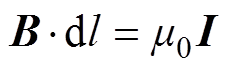（4）
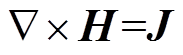（5）
式中，H为磁场强度；I为流过闭合线圈的电流；J为电流密度。在有限元仿真软件中进行磁场分析，设置不同的电流值，仿真计算得到空间内不同区域的磁感应强度及相应的磁场梯度。
在扫描过程中，非磁化饱和区域内的磁性纳米粒子处于一个由与空间位置相关的梯度静磁场
以及一个与驱动时间相关的均匀交变磁场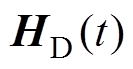
叠加产生的局部磁场
中，表示为
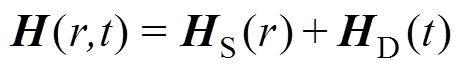（6）在三维空间中，区域r内与时间t相关的磁场可以表示为
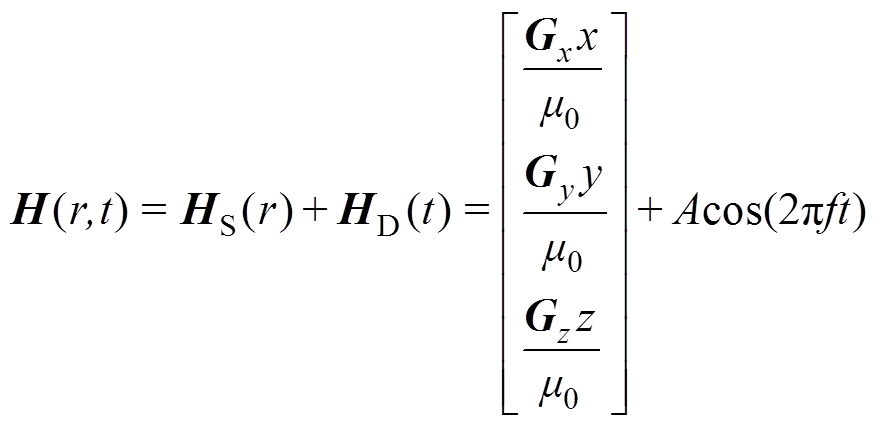（7）
式中，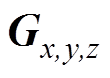
为不同方向的磁场梯度；
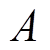为交变磁场幅度；
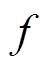为交变磁场频率。
电流与磁场间的关系如图8所示。为了获得MPI所需的1T/m的磁场梯度，首先分析用于产生梯度静磁场的平面梯度线圈电流对磁场梯度的影响。分别计算施加电流为30A、40A、50A、60A、70A时，xy截面y=0、x=-5～5cm二维截面上的磁感应强度，如图8a所示，共5组每组125个数据点。利用该数据分别计算不同电流情况下的磁场梯度，如图8b所示。
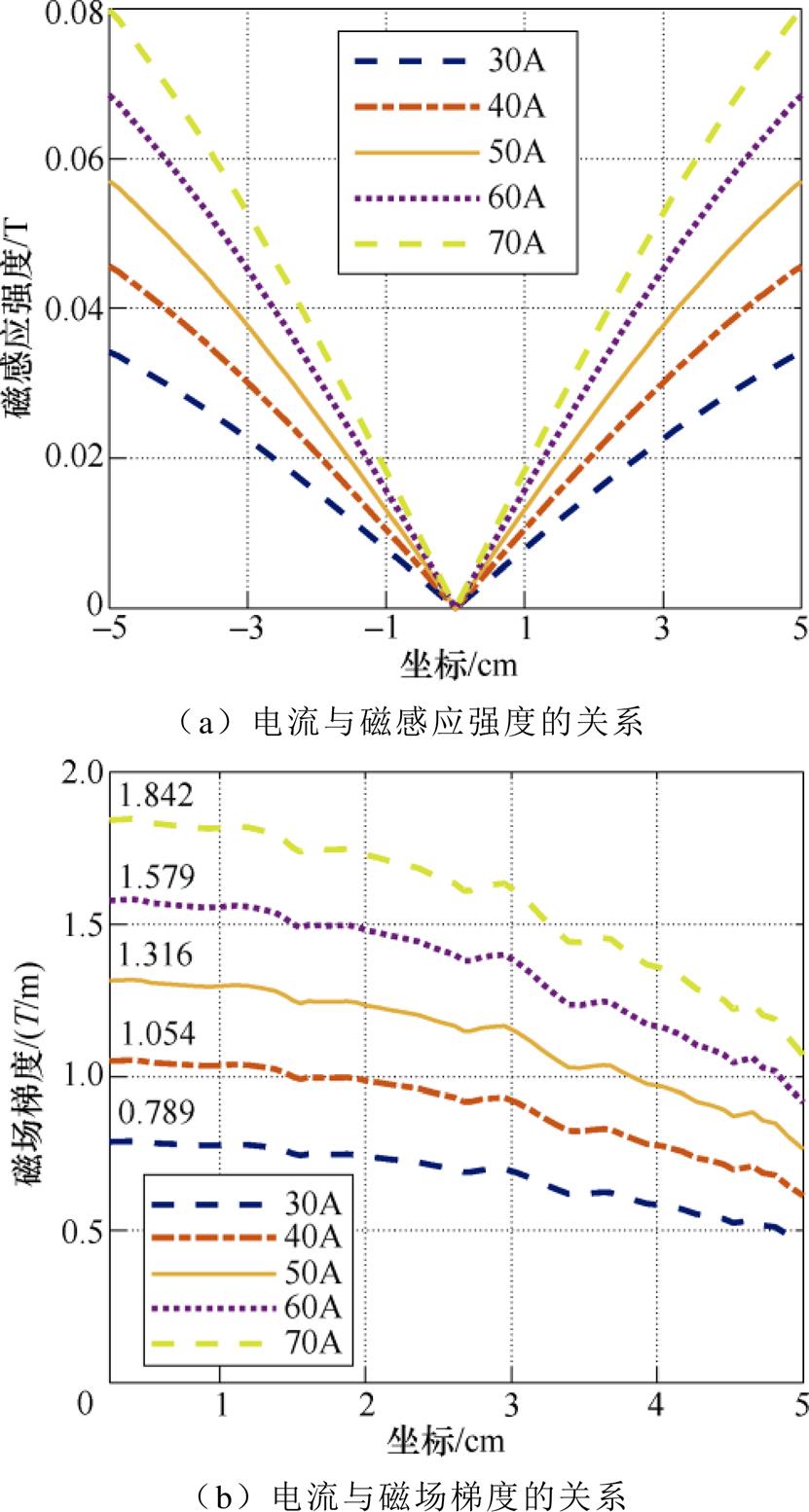
图8 电流与磁场间的关系
Fig.8 Relationship between current and magnetic field
当电流越大时，磁感应强度越大，且离坐标中心越远，磁感应强度差越大，但不同电流下呈现的磁场趋势相同，均随着与坐标中心距离的减小而线性减小。从磁场梯度角度看，平面梯度线圈产生的磁场梯度并不均匀，随着与FFL的距离增大而减小。同时，电流越大、磁场梯度越大，呈现近似线性递增的关系。在磁场梯度尽可能满足MPI分辨率需求的前提下，采用较小平面梯度线圈电流，本文采用50A梯度场电流，此时磁场梯度为1.316T/m。
分析用于产生均匀交变磁场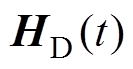的驱动线圈电流对磁场梯度的影响。由式（7）可知，局部磁场由梯度静磁场和均匀交变磁场产生，如果梯度磁场足够大，则交变磁场对原磁场的梯度影响可以忽略。因此根据本文所设计的系统扫描方式，线型零磁场沿y方向延伸（
）并在驱动线圈的驱动下沿x方向移动，此时满足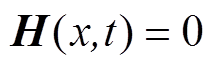
，FFL的位置可以描述为
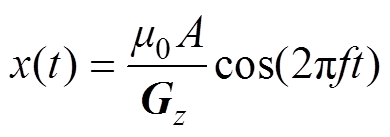（8） 因此，根据式（8）可知，FFL沿着x轴方向在区域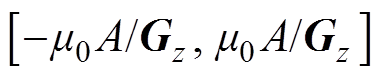
上振荡，完成平行扫描的工作。其中，FFL在区域中心具有最高速度，在边缘速度降低。分别研究FFL的最大平移距离与驱动线圈交变磁场幅度关系，及其与梯度静磁场产生的梯度之间的关系。最大移动距离与交变磁场幅度及梯度的关系如图9所示，交变磁场的幅度与最大平移距离呈正比，同时梯度静磁场会阻碍FFL的平移，即选择场梯度越大，最大平移距离越小。理论上，在1T/m的梯度静磁场中，施加8 875A/m的驱动磁场（即幅值为100A的驱动场电流），FFL的最大移动距离为0.011 2m。
图9 最大移动距离与交变磁场幅度及梯度的关系
Fig.9 Relationship between maximum moving distance and amplitude and gradient of alternating magnetic field
图10所示为FFL在梯度为1.316T/m的磁场中，不同驱动电流下，FFL在x轴方向下的最大平移位置，及x方向磁感应强度与移动坐标之间的关系。图中的左侧为xy截面的磁感应强度分布，用虚线标注白色亮线即为FFL，右侧为x方向的磁感应强度数值与成像区域坐标之间的关系，其中磁感应强度最小的坐标位置同样用虚线标注，即为FFL所处的位置，与左图相对应。
图10 不同驱动电流下的磁感应强度
Fig.10 Magnetic induction intensity map under different driving currents
根据结果可知，当施加正向电流时，线型零磁场向x轴正方向移动。移动方向与驱动线圈通入电流的方向有关，且电流绝对值越大，移动距离越大。
分析不同的驱动场电流与FFL最大移动距离之间的关系，对仿真结果与理论计算进行比较分析，驱动电流与移动距离的关系如图11所示。仿真结果与理论计算结果一致，驱动电流与移动距离呈线性递增的关系。因此，通过移动距离与电流的关系，可以根据所需距离设置不同的采样频率，达到等距扫描的目的。在扫描面积尽可能大的前提下，采用较小的驱动电流。
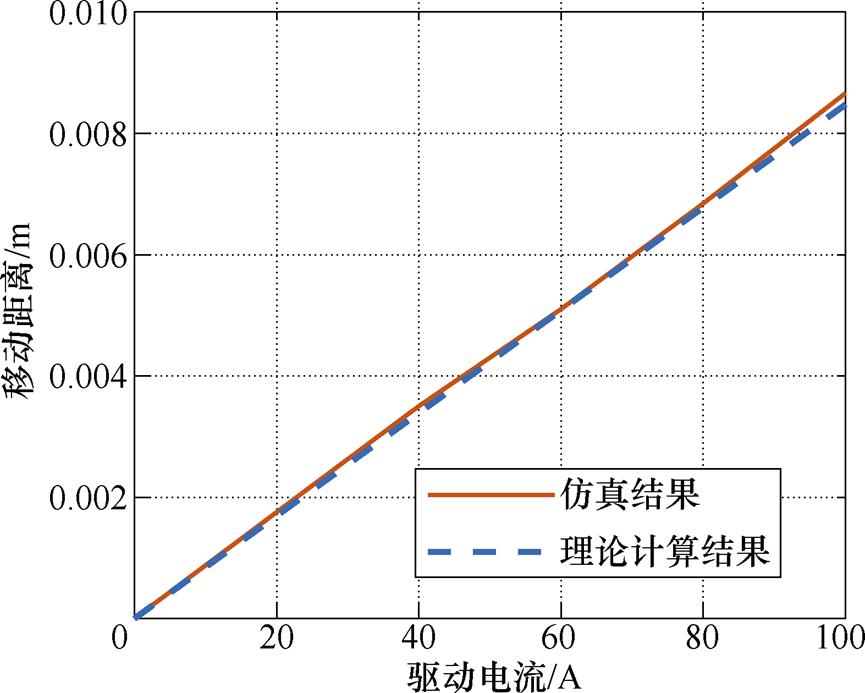
图11 驱动电流与移动距离的关系
Fig.11 Driving current and moving distance
最终确定两者的施加电流，使用50A的平面梯度线圈电流，幅值为100A的驱动电流，磁场梯度为1.316T/m，采用横向扫描及纵向扫描叠加的扫描方式，成像面积为17mm×17mm，通过加大驱动电流以及增加低频焦点场的方式，可以进一步扩大成像面积。
线型零磁场周围的磁场梯度可以反映出零磁场的精度，从而决定成像分辨率。根据本文所设计的开放式线型零磁场，施加50A平面梯度线圈电流以及幅值为100A驱动线圈电流。
对本文所设计的开放式线型零磁场线圈布置结构进行仿真分析，磁场分布仿真计算结果如图12所示。其中，中间的长方体部分为成像区域，磁感应强度值最低的深蓝色细线即为FFL。对仿真得到的空间磁场数据进行线型零磁场均匀性分析、分辨率分析以及扫描成像结果分析。
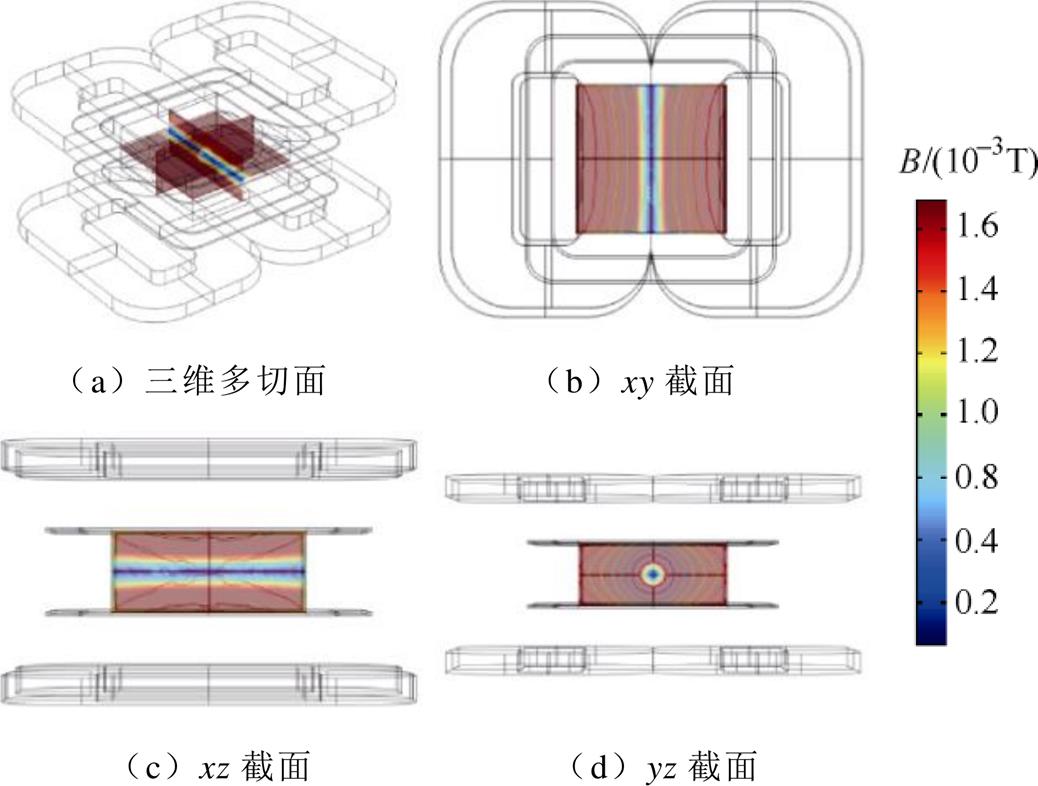
图12 磁场分布仿真计算结果
Fig.12 Magnetic field distribution simulation calculation result
FFL的纵向均匀性在很大程度上影响了最后的成像质量，不同的成像算法对FFL的均匀性要求不同。分析开放式零磁场线圈系统所构造的零磁场线的纵向均匀性，如图13所示为FFL在x=0.2mm处沿y轴20cm的磁感应强度曲线。该曲线表示FFL边缘处的磁感应强度情况，可以清楚地看到，在y=0点附近的磁感应强度比较稳定，长度为10cm的FFL其磁感应强度变化稳定在0.04mT内，当FFL增大时，头尾两侧的磁感应强度逐渐减小，因此根据其磁场特性，以及重建算法的要求，可以选择相应的FFL长度以保证磁场的均匀性。针对本文所设计的线型零磁场，一般选择两虚线段以内的FFL长度进行扫描成像，可以看出其均匀性较好，满足MPI所需的磁场要求。
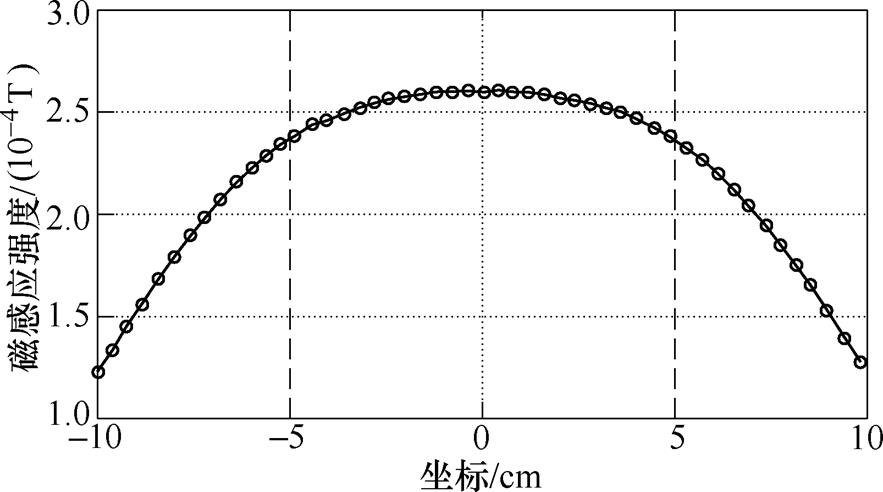
图13 x=0.2mm处沿y轴20cm磁感应强度曲线
Fig.13 20cm magnetic induction curve along the y axis at x=0.2mm
MPI利用位于零磁场中的磁性纳米粒子发射出的粒子信号进行成像，因此由磁场梯度大小所决定的FFL磁化响应未饱和区域大小决定了磁性粒子成像系统的成像分辨率。根据FWHM的定义，计算不同粒径的磁性纳米粒子在磁化饱和时所需要的磁场大小，再利用仿真得到的磁场分布数据，计算在磁场梯度为1.316T/m下的分辨率，计算的结果见表2。当径粒为60nm时，分辨率为0.304mm，达到亚毫米级，且仿真计算得到的分辨率数值与式（3）的理论计算结果相近，理论计算的分辨率更高，满足MPI的高分辨率需求。同时因为成像的扫描方式为横竖双方向扫描，因此该分辨率即为成像分辨率。
表2 不同粒径磁性纳米粒子在1.316T/m下的分辨率
Tab.2 Imaging resolution of magnetic nanoparticles with different particle sizes at 1.316T/m
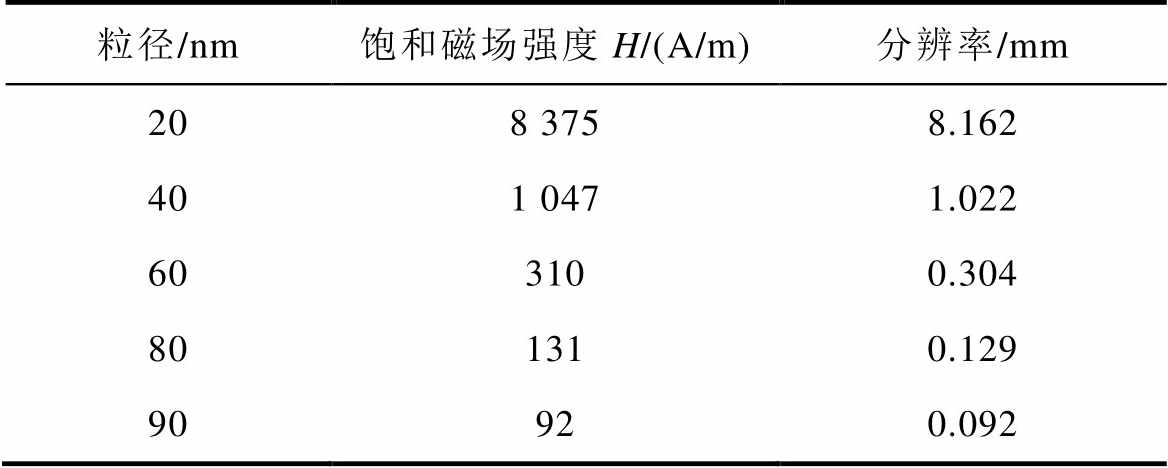
粒径/nm饱和磁场强度H/(A/m)分辨率/mm 208 3758.162 401 0471.022 603100.304 801310.129 90920.092
根据所计算的成像分辨率，计算一个驱动场周期（0.05s）下的扫描数据，设置采样间隔为0.000 3s，针对一个17mm×17mm的成像区域，利用90nm粒径的磁性纳米粒子悬浮液进行实验，设置梯度电流为直流50A，驱动电流为交变电流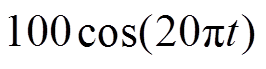
A，在1.316T/m的梯度磁场下进行成像实验，计算一个驱动场扫描周期的时间，其成像精度为0.1mm× 0.1mm。对于不同大小以及形状的磁性纳米粒子质量分数模型进行仿真及扫描成像实验。
利用仿真计算得到的z方向磁场强度，采用系统矩阵法进行图像重建，使用MPI信号方程对接收信号进行建模，得到横向平移扫描和纵向平移扫描下的一维时间信号，并采用系统矩阵法进行重建，将粒子信号从时间域还原到空间域。具体的图像扫描重建过程如图14所示，两个方向下的扫描重建粒子信号为一维时间信号，将粒子信号从时间域还原到空间域。针对单粒子的粒子质量分数模型来看，重建的粒子信号均在粒子所处的横轴及纵轴的坐标处呈现出信号峰值。磁性粒子质量分数模型及其二维成像如图15所示。图15a中的黑色区域表示填充磁性纳米粒子悬浮液，且每个像素内粒子质量分数一致，将二者依据线形零磁场特性进行图像重建，最后得到的粒子质量分数信号重建图像如图15b所示。
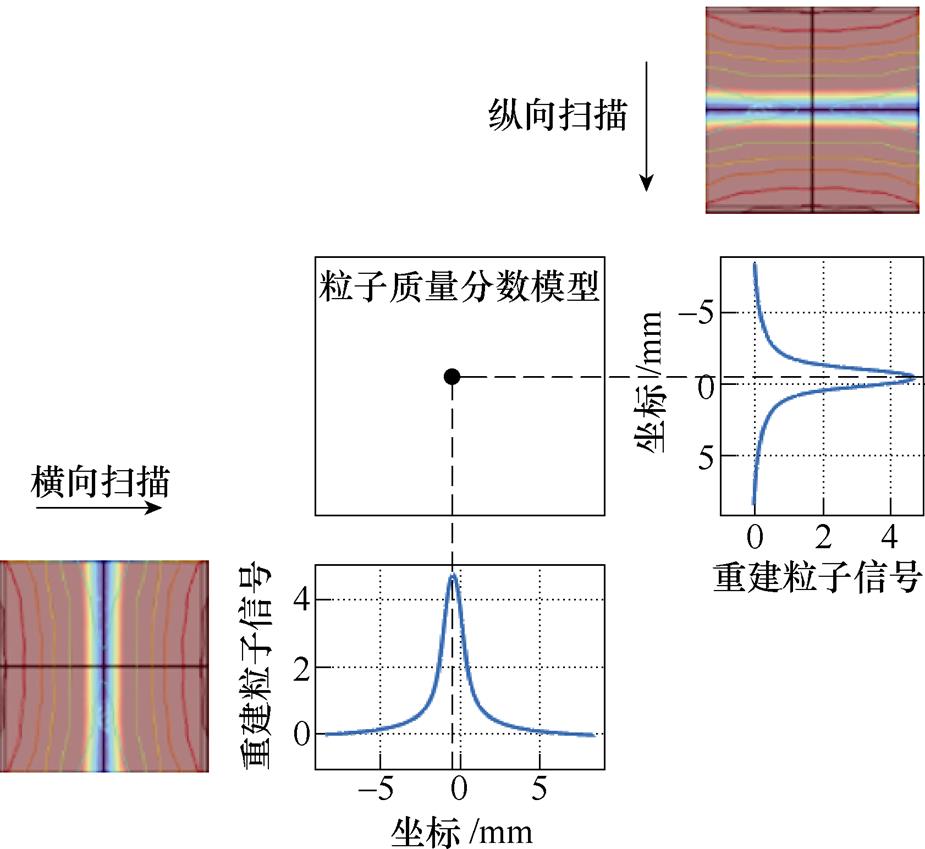
图14 图像扫描重建过程
Fig.14 Image scanning reconstruction process
图15 磁性粒子质量分数模型及其二维成像
Fig.15 Magnetic particle quatity score model and its two-dimensional imaging
对六种不同粒子质量分数模型进行重建。对比不同大小的质量分数模型可以看出，本文所设计的开放式线型零磁场可以清晰地分辨出0.1mm尺寸的磁性纳米粒子质量分数模型，同时其对模型大小的成像准确度也随着模型的增大而提高。对比不同形状的质量分数模型，可以看出当模型尺寸为0.5mm时，图像边缘清晰且形状大小准确。如图15c所示，从图像的粒子质量分数信号可以看出，粒子尺寸越大，区域内聚集的粒子越多，其质量分数信号也相应增大。根据结论证明，利用本文所设计的开放式线型零磁场进行扫描成像即可得到粒子质量分数位置的清晰图像。
本文针对现阶段成像系统的开放式扫描结构问题，利用高灵敏度的线型零磁场，提出了一种基于开放式线型零磁场设计的MPI方法，实现了高成像分辨率的线型零磁场扫描成像方法。具体结论如下：
1）在MPI中，要实现亚毫米级分辨率，理论上所需的磁场梯度要大于1.093T/m。根据该精度要求，本文采用开放式线圈结构，与封闭式结构相比，在增加舒适度的同时，减小了对被测目标体积的限制，进而扩大了成像面积。
2）采用线型零磁场的方式，与零磁场点相比，不仅提高了成像分辨率，也在一定程度上加快了成像速度，同时确保了线型零磁场良好的均匀性。
3）针对平移扫描方式，利用数值计算及仿真两种方式对平移距离与驱动电流的关系进行分析，其两种计算方式结果相同，平移距离与驱动电流呈正比关系，因此通过对驱动电流的控制，可以实现MPI的等距平扫。
4）采用这种设计方法后，其理论的成像分辨率可小于亚毫米级分辨率。最后重建的图像分辨率为0.1mm×0.1mm，成像区域为17mm×17mm，通过横向扫描与纵向扫描叠加的方式，可以实现基于开放式线型零磁场的高成像分辨率扫描成像。理论证明了开放式线型零磁场扫描方式用于磁性粒子成像的可行性。
参考文献
[1] Weizenecker J, Borgert J, Gleich B. A simulation study on the resolution and sensitivity of magnetic particle imaging[J]. Physics in Medicine and Biology, 2007, 52(21): 6363-6374.
[2] Gleich B, Weizenecker J. Tomographic imaging using the nonlinear response of magnetic particles[J]. Nature, 2005, 435(7046): 1214-1217.
[3] Bulte J W M, Walczak P, Bernard S, et al. Deve- loping cellular MPI: initial experience[C]//Inter- national Workshop on Magnetic Nanoparticles- particle Science, Imaging Technology, Germany, Lübeck, 2010: 201-204.
[4] Cetin S, Saritas E U, Unal G. Vessel tractography for magnetic particle imaging angiography[C]//IEEE 5th International Workshop on Magnetic Particle Imaging (IWMPI), Turkey, Istanbul, 2015: 1.
[5] Sigovan M, Boussel L, Sulaiman A, et al. Rapid- clearance iron nanoparticles for inflammation imaging of atherosclerotic plaque: initial experience in animal model[J]. Radiology, 2009, 252(2): 401-409.
[6] Weizenecker J, Gleich B, Rahmer J, et al. 3D real- time in vivo magnetic particle imaging[J]. Physics in Medicine and Biology, 2009, 54(5): 1-10.
[7] Weizenecker J, Gleich B, Borgert J. Magnetic particle imaging using a field free line[J]. Journal of Physics D: Applied Physics, 2008, 41(10): 105009.
[8] Tobias K, Marlitt E, Sven B, et al. Efficient generation of a magnetic field-free line[J]. Medical Physics, 2010, 37(7): 3538-3540.
[9] Knopp T, Erbe M, Sattel T F, et al. Generation of a static magnetic field-free line using two Maxwell coil pairs[J]. Applied Physics Letters, 2010, 97(9): 092505.
[10] Knopp T, Biederer S, Sattel T F, et al. 2D model- based reconstruction for magnetic particle imaging[J]. Medical physics, 2010, 37(2): 485-491.
[11] Knopp T, Rahmer J, Sattel T F, et al. Weighted iterative reconstruction for magnetic particle imaging[J]. Physics in Medicine and Biology, 2010, 55(6): 1577-1589.
[12] Enpuku K, Miyazaki T, Morishita M, et al. Narrowband magnetic nanoparticle imaging using cooled pickup coil and gradient field[J]. Japanese Journal of Applied Physics, 2015, 54(5): 057002.
[13] Morishige T, Mihaya T, Bai S, et al. Highly sensitive magnetic nanoparticle imaging using cooled-Cu/ HTS-superconductor pickup coils[J]. IEEE Transa- ctions on Applied Superconductivity, 2014, 24(4): 1-5.
[14] Sasayama T, Tsujita Y, Morishita M, et al. Three- dimensional magnetic nanoparticle imaging using small field gradient and multiple pickup coils[J]. Journal of Magnetism and Magnetic Materials, 2016, 427(1): 144-150.
[15] Yuya T, Masahiro M, Teruyoshi S, et al. Three- dimensional magnetic particle imaging utilizing multiple pickup coils and field-free line[C]//16th International Superconductive Electronics Conference (IEICE), Naples, Italy, 2017: 1-3.
[16] Rahmer J, Weizenecker J, Gleich B, et al. Signal encoding in magnetic particle imaging: properties of the system function[J]. BMC Medical Imaging, 2009, 9(1): 1-21.
[17] Den Dekker A J, Van den Bos A. Resolution: a survey[J]. Journal of the Optical Society of America, 1997, 14(3): 547-557.
[18] Houston W V. A compound interferometer for fine structure work[J]. Physical Review, 1927, 29(3): 478-484.
[19] Knopp T, Buzug T M. Magnetic particle imaging: an introduction to imaging principles and scanner instrumentation[M]. New York: Springer, 2012.
[20] Chikazumi S. Physics of magnetism[M]. New York: John Wiley & Sons, 1964.
[21] Kaethner C, Ahlborg M, Grafe K, et al. Asymmetric scanner design for interventional scenarios in magnetic particle imaging[J]. IEEE Transactions on Magnetics, 2015, 51(2): 1-4.
[22] 汪泉弟, 康健炜, 王赢聪, 等. 磁谐振无线电能传输系统空间磁场的时空特性[J]. 电工技术学报, 2018, 33(19): 4486-4495.
Wang Quandi, Kang Jianwei, Wang Yingcong, et al. Temporal and spatial characteristics of magnetic fields in magnetic resonant wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4486-4495.
[23] Lü Xing, Wang Zheng, Yang Wenhui. Field free line generation for magnetic particle imaging based on the mirror rule[C]//IEEE 2013 6th International Con- ference on Biomedical Engineering and Informatics (BMEI), Hangzhou, China, 2013: 43-47.
[24] 贺中华, 何为, 贺玉成, 等. 皮肤烧伤深度检测的单边核磁共振浅层成像磁体系统[J]. 电工技术学报, 2019, 34(3): 449-458.
He Zhonghua, He Wei, He Yucheng, et al. Unilateral nuclear magnetic resonance superficial imaging magnet system for skin burn depth assessment[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 449-458.
[25] 郑广君. 适应需求侧管理的高效中距离磁共振式电动汽车无线充电线圈优化设计[J]. 电工技术学报, 2017, 32(增刊1): 209-216.
Zheng Guangjun. Optimization design of efficient middle-distance magnetic-resonance wireless charge coil suitable for electric vehicle charging[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(S1): 209-216.
Design and Analysis of Magnetic Field-Free Line in Magnetic Particle Imaging
Abstract Magnetic particle imaging is a tracer imaging technique with high imaging resolution. Aiming at the open scanning problem of the current imaging system, a high-resolution two-dimensional scanning imaging method is realized by a highly sensitive magnetic field-free line. A magnetic field-free line with an open coil structure is designed. The magnetic field-free line is constructed by gradient static magnetic field to determine the position of the tracer, and the uniform alternating magnetic field is used for translation scanning of magnetic field-free line. The coil structure is analyzed in detail. Firstly, the current driving method of the magnetic particle imaging coil system for realizing high resolution is determined. Then the finite element simulation calculation analysis of the open magnetic field-free line scanning method is carried out. Finally, according to the relationship between the driving mode and the range of the translation scanning region, the imaging experiment of the particle quality score model is carried out. The results show that the open coil structure of the magnetic field-free line can realize high resolution imaging of magnetic nanoparticle tracer in the imaging area of 17mm×17mm in a gradient magnetic field of 1.316T/m, the resolution can reach sub-millimeter. It is proved that the magnetic field-free line scanning method is feasible for magnetic particle imaging.
keywords：Magnetic particle imaging, open, imaging resolution, magnetic field-free line, finite element simulation
DOI: 10.19595/j.cnki.1000-6753.tces.190472
中图分类号：TM153
刘洋洋 女，1995年生，硕士研究生，研究方向为生物医学电磁科学与技术。E-mail: liuyangyang_sut@163.com
杜 强 男，1975年生，讲师，硕士生导师，研究方向为生物电工技术。E-mail: duqiang@sut.edu.cn（通信作者）
收稿日期 2019-04-22
改稿日期 2019-10-29
国家自然科学基金（51377109）和辽宁省自然科学基金计划（2019-ZD-0204）资助项目。
（编辑 陈 诚）