（1）摘要 该文引入小磁滞回线下磁能损耗数学模型，使用AMH-1M-S型动态磁特性测试系统测量了Fe-Co-V、Terfenol-D与Fe-Ga合金样品的高频磁滞回线，利用实验测试结果结合数学模型对比分析了三种材料的磁导率幅值、介质损耗因数、介质储能和电磁损耗变化规律。当励磁磁场频率为50kHz时，随着磁感应强度的增加，Terfenol-D和Fe-Ga合金的介质损耗因数近似线性增加，三种合金样品的电磁损耗均增大。当磁感应强度为0.03T时，随着励磁磁场频率的增加，Fe-Co-V、Fe-Ga合金磁导率幅值都先增大后减小，Terfenol-D合金的介质储能增加最快并且其电磁损耗随频率增速最快。在1～40kHz内Fe-Ga合金的电磁损耗高于Fe-Co-V合金，在40～60kHz内Fe-Ga合金电磁损耗低于Fe-Co-V合金。该文结果为磁致伸缩材料的电磁损耗分析与高频器件设计提供了依据。
关键词：高频 磁滞回线 磁导率 介质损耗因数 电磁损耗
先进的软磁材料表现出高频率、高磁通密度以及微型化、多功能两种并存的发展格局，一些先进的电工软磁材料得到快速发展，特别是以Fe-Co-V、Terfenol-D与Fe-Ga合金为代表的磁致伸缩材料被广泛应用，对电力器件的影响深远[1-3]。Fe-Co-V合金具有极高的饱和磁感应强度（2.4T）和居里温度（980～1 100℃）、饱和磁致伸缩系数（60～100× 10-6）大，适用于质量轻、体积小的航空元器件（如继电器、电磁铁、微特电机等），但该合金的电阻率（0.27mW·m）低，在高频下使用时受磁能损耗影响较大[4-5]。Terfenol-D合金是一种磁致伸缩系数（2 000× 10-6）大、能量密度高和响应速度快的磁致伸缩材料，在大功率超声（f ≥20kHz）、声呐等应用领域有显著优势，然而该合金材料在高频驱动过程中产生磁滞，影响器件的能量转换效率[6-8]。Fe-Ga合金具有磁导率高、应力灵敏度高、饱和磁场较低等优点，广泛应用于新型传感器件、振动发电领域，而影响Fe-Ga合金器件性能的关键指标是Fe-Ga合金的磁导率和电磁损耗[9-10]。因此，三种不同磁致伸缩材料在高频领域进行器件设计时，高频磁能损耗分析是研究与其相关的合金器件结构设计和应用的基础。
文献[11]研究了环状Galfenol合金的高频磁特性，重点分析了材料的磁导率、矫顽力、剩余磁感应强度和损耗随频率的变化关系。文献[12]研究发现，Tbdyfe合金的电磁损耗随频率的变化曲线是抛物线型，并且涡流损耗占损耗的主要部分，利用Tbdyfe合金粉末制备了一种新型复合材料，电磁损耗受频率影响不大，主要损耗为磁滞损耗。文献[13]在0.2～8GHz的频率范围内测量了软磁材料FeCoB薄膜中磁导率随外磁场强度的变化规律。文献[14]建立了在交流励磁作用下超磁致伸缩材料的磁场函数，发现驱动频率将影响磁场的大小和滞后性，并且得到了适用于中低频磁能损耗计算的数学模型，分析了驱动磁场频率对复数磁导率、磁场的滞回特性以及磁能损耗的影响，但文中并没有分析材料高频情况下的电磁特性。文献[15]将传统的J-A磁滞模型与瞬态涡流和剩余损耗模型相结合，建立了J-A动态磁滞模型，该模型需要的参数较多，实际工程中应用较少。文献[16]提出一种改进铁耗计算模型，能够反映出高频高磁密时叠片材料内的涡流趋肤效应、动态磁滞回线和畴壁运动的变化规律，并且实验测量结果与计算结果有较好的对应性。文献[17]改进了Steinmetz损耗方程，提出在对称和非对称磁感应波形下对不同软磁材料的损耗预测方法，经过实验测量与计算结果对照，证明了该方法的工程实用性。文献[18]设计了一种双线圈铁镓合金磁滞伸缩换能器，利用磁能与机械能的转换关系分析了该换能器在不同磁场频率下的能量储能、电磁损耗以及机械能变化规律。
由于磁致伸缩材料的多样性以及高频下磁滞特性的复杂性，不同磁致伸缩材料的损耗特性随频率变化情况对比分析较少。本文针对在相同工程背景下磁致伸缩器件在设计过程中所遇到的材料选取问题，从不同磁致伸缩材料的磁导率、介质损耗因数、介质储能和电磁损耗等方面对比分析Fe-Co-V、Terfenol-D与Fe-Ga合金的磁能表现，引入小磁滞回线磁能损耗模型，利用AMH-1M-S型动态磁特性测试系统测量了典型磁致伸缩材料Fe-Co-V、Terfenol-D、Fe-Ga合金在不同励磁磁场频率和不同磁感应强度下的动态磁滞回线，对比分析三种材料在不同条件下磁能损耗影响因素，为磁致伸缩新型器件的优化设计和应用提供了理论与实验参考。
根据瑞利定理，磁致伸缩材料在不同的磁化过程中，低磁场下的磁滞回线可以通过解析式来表达，特别是磁感应强度峰峰值决定的小磁滞回线，可以用上升分支和下降分支的方程来描述[19]。
上升分支
（1）下降分支
（2）
式中，a、b为可逆和不可逆瑞利常数；H为磁场强度；B为磁感应强度；（Hp, Bp）为磁滞回线尖端点，描述了初始磁化曲线遵循以下规律
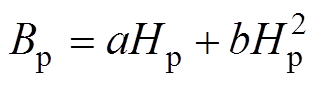（3）式中，Bp为正弦磁感应强度峰峰值。
在极低磁场的限制下，磁化曲线呈线性，常数a与初始磁化率ci成正比
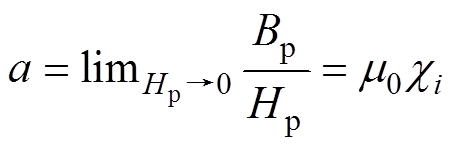（4）对磁滞回线的积分可以得到单位体积的磁滞损耗为
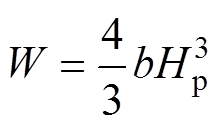（5）
它可以等效地表示为磁感应强度峰峰值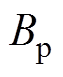
的函数，有
（6）若式（3）中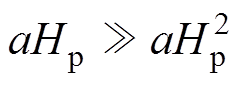
，即线性导向占主导地位，那么式（5）可以近似为
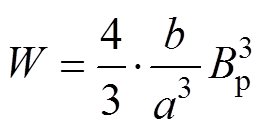（7）
若式（3）中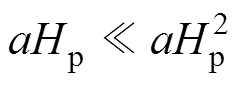
，则式（5）近似为
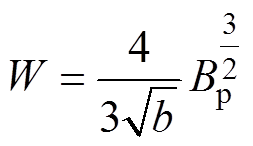（8）通过验证可以得出在B-H平面中磁滞回线的任何位置，a和b参数值取决于之前磁场的历史信息、移动的磁畴壁数量和能量分布状况。如果磁场的幅值足够低，使得式（4）的线性近似合理，可以实现将自感和互感的理念应用于任何具有连接线圈的样品，以这种方式可以分析磁心的损耗情况。在瑞利区域内，当样品处在低磁场中，给一个封闭的磁性材料样本施加一个交变的弱磁场，可以用复数磁导率来近似材料的本构关系，有
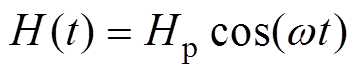（9）
由于样品中涡流的限制，样品的磁感应强度在时间上滞后磁场强度，有
（10）式中，d 为磁心损耗引起的电压与电流的相位差，代表磁感应强度和磁场强度的滞后关系。
将式（10）表示为两个相位相差90°正弦波叠加，即
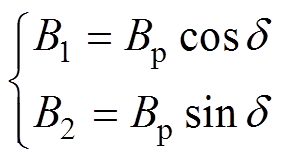（11）复数形式为
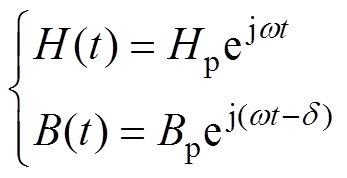（12）
由式（12）可以得到复数磁导率[20]为
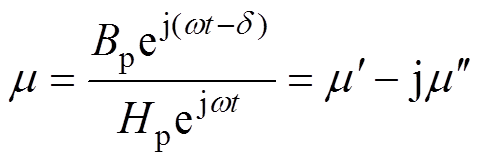（13）其中
式中，
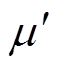和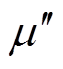
分别为复数磁导率的实部和虚部。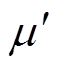表示磁场作用下产生的磁化强度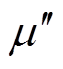，表示在磁场作用下材料磁偶极矩引起的损耗。
介质损耗因数可表示为
（14）式中，介质损耗因数是磁致伸缩材料在交变磁场中每周期损耗的能量与储能的能量之比，用来反映软磁材料在交变磁化时磁能的损耗和存储性能。
此时单位体积的电磁损耗公式可以表示为
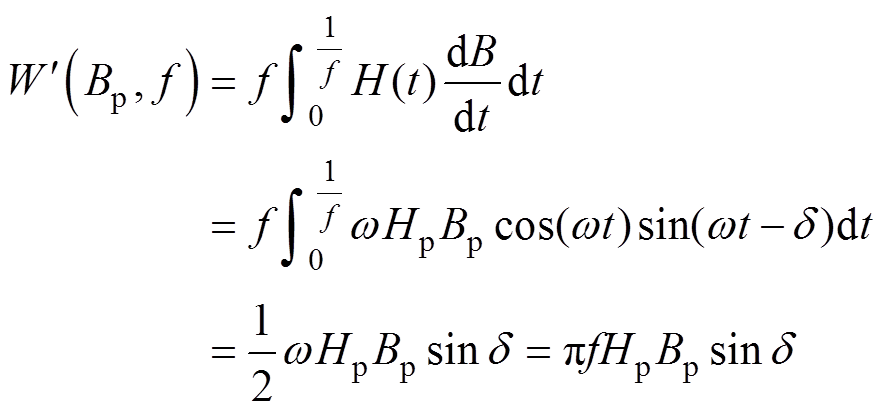
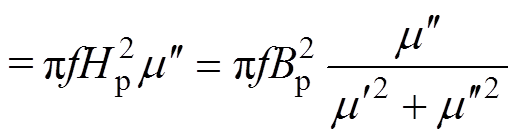（15）
其中
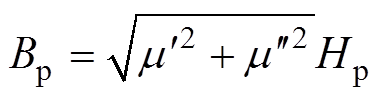
式（15）表明，在给定磁感应强度峰峰值的情况下，可以用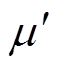和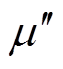来近似磁滞曲线的形状和面积，从而可以计算磁能损耗。
单位质量电磁损耗为
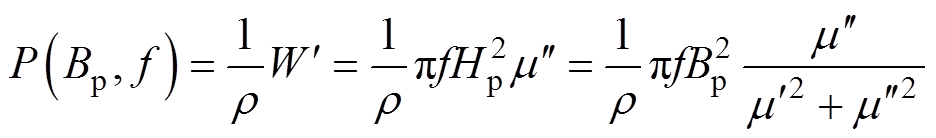（16）式中，r 为材料密度。
单位质量的介质储能为
（17）式（16）和式（17）都是通过复数磁导率的实部和虚部计算得到，表明了磁化程度和磁偶极矩的变化对不同磁致伸缩材料单位质量电磁损耗和介质储能的影响。
实验中，Fe-Co-V、Terfenol-D与Fe-Ga合金均为环状样品，测试样品的内径为8.60mm，外径为11.93mm，高为3.53mm，三种样品的驱动线圈选用线径为0.50mm的漆包线20匝，感应线圈选用线径为0.15mm的漆包线10匝。三种合金样品的化学分子式分别为Fe49Co49V2、Tb42.3Dy17.7Fe40和Fe83Ga17，磁化方向沿样品轴向。
材料动态磁特性测量原理如图1所示，该实验系统主要是由计算机、信号发生器、功率放大器、磁通计、数据采集系统、采样电阻等组成。开始工作时通过计算机界面控制信号发生器发生一定频率的正弦交流小信号，再经功率放大器后施加在励磁线圈上，在励磁线圈及其周围产生一个交变磁场，该磁场的频率与励磁电流频率相同，通过环形测试样品与励磁线圈产生电磁耦合作用，在感应线圈两端产生感应电动势，感应的信号经过磁通计传入数据采集系统，同时通过采样电阻将励磁线圈的信号也传入数据采集系统，最后采集系统中的数据导出到计算机中，可以绘制相应的磁滞曲线。实验测试平台是一个集成电气柜，如图2所示。该测试平台用来测量磁致伸缩材料的交直流磁特性，校准测量时，能够保证磁导率的误差在±1.5%，电磁损耗的误差在±3%。
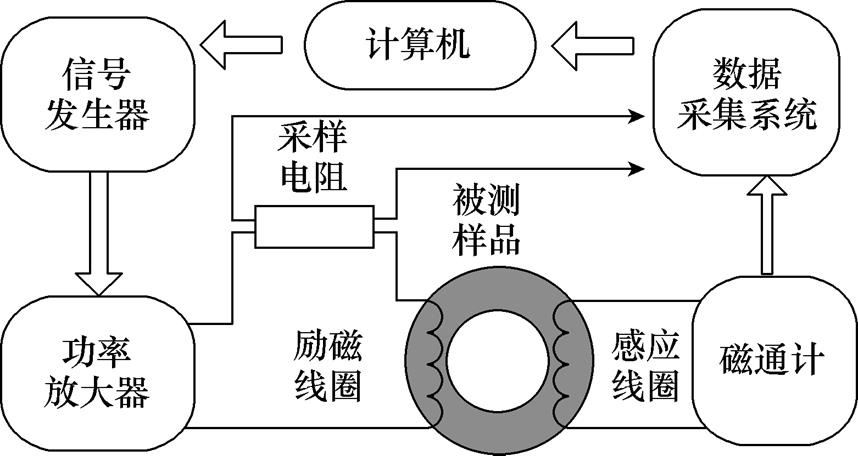
图1 材料动态磁特性测量原理
Fig.1 Schematic diagram of dynamic magnetic characteristics measurement of annular soft magnetic material
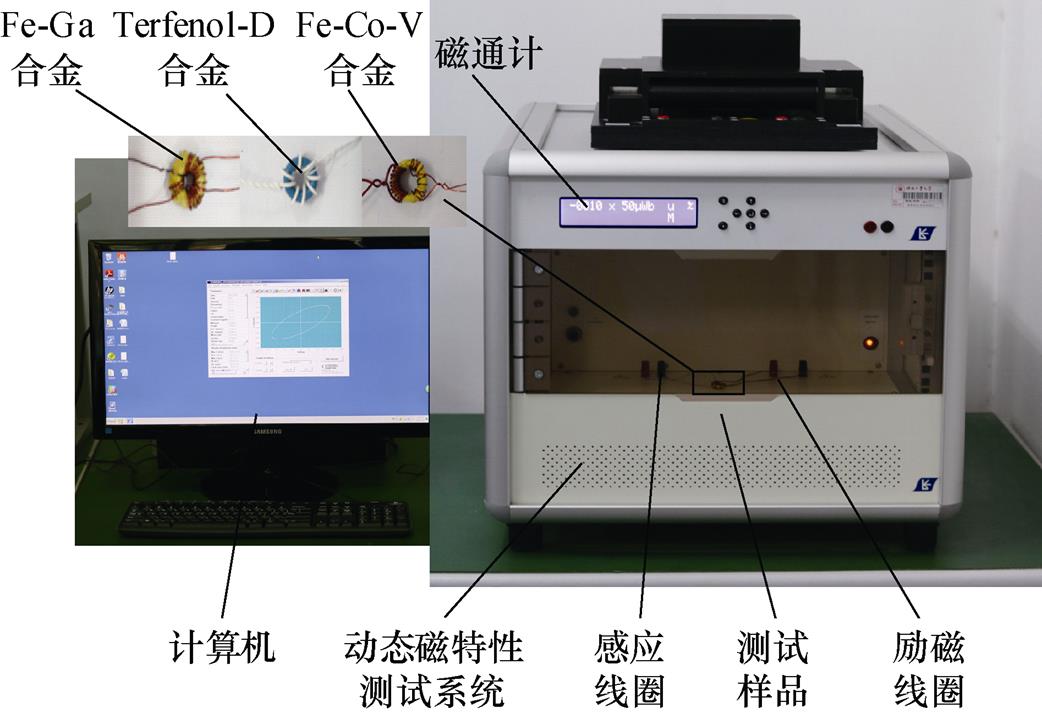
图2 实验测试平台
Fig.2 Experimental test platform
考虑到不同磁致伸缩材料的磁能损耗主要与合金样品工作环境中励磁磁场频率和所施加的磁感应强度有关，本文通过对数学模型的推导和设备准确度的校验，对Fe-Co-V、Terfenol-D与Fe-Ga合金的三种样品在相同励磁磁场频率下增大磁感应强度和相同磁感应强度下增加励磁磁场频率的情况下分别测试，为了充分分析三种合金材料的高频磁能表现，并结合目前不同材料的应用场合，实验选用测试的频率范围为1～60kHz，最大磁感应强度变化范围为0.010～0.030T。分别绘制出三种合金样品在不同情况下的系列磁滞回线。利用式（13）分析样品磁导率幅值变化情况，利用式（14）分析介质损耗因数变化规律，通过式（16）和式（17）分析材料单位质量的电磁损耗和介质储能。文中对比分析的主要目的是在同一种工程背景应用的情况下，从材料的磁滞特性及磁能损耗方面优化选择出最佳的磁致伸缩材料。
图3～图5为交变励磁磁场频率50kHz，最大磁感应强度分别为0.010T、0.015T、0.020T、0.025T、0.030T情况下测得的Fe-Co-V、Terfenol-D、Fe-Ga合金的动态磁滞回线。三种样品在磁场频率一定时，磁滞曲线围成的小磁滞同心椭圆环的面积随着磁感应强度的增大而逐渐增大，并且每种材料的剩余磁感应强度、矫顽力和最大磁场强度都逐渐增大。将每组图形中小磁滞回线的顶点连接起来，可以看出三种样品的动态磁化曲线近似呈线性变化，该磁化过程处于初始磁化阶段的可逆磁化过程，样品内部主要是可逆转动磁化和可逆壁移磁化。
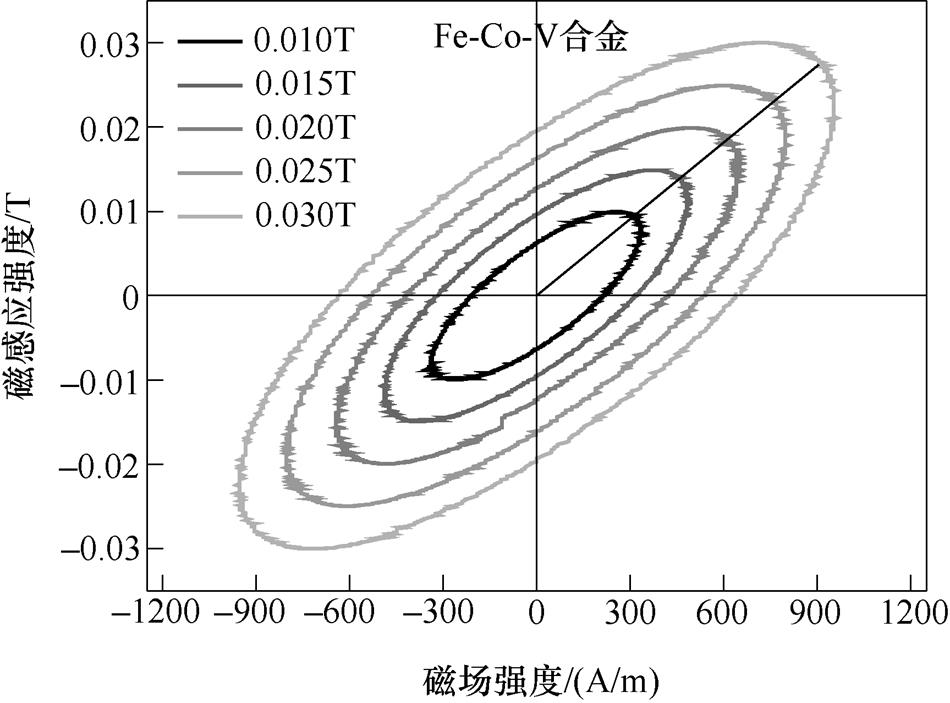
图3 Fe-Co-V合金的动态磁滞回线
Fig.3 Dynamic hysteresis loops of Fe-Co-V alloy
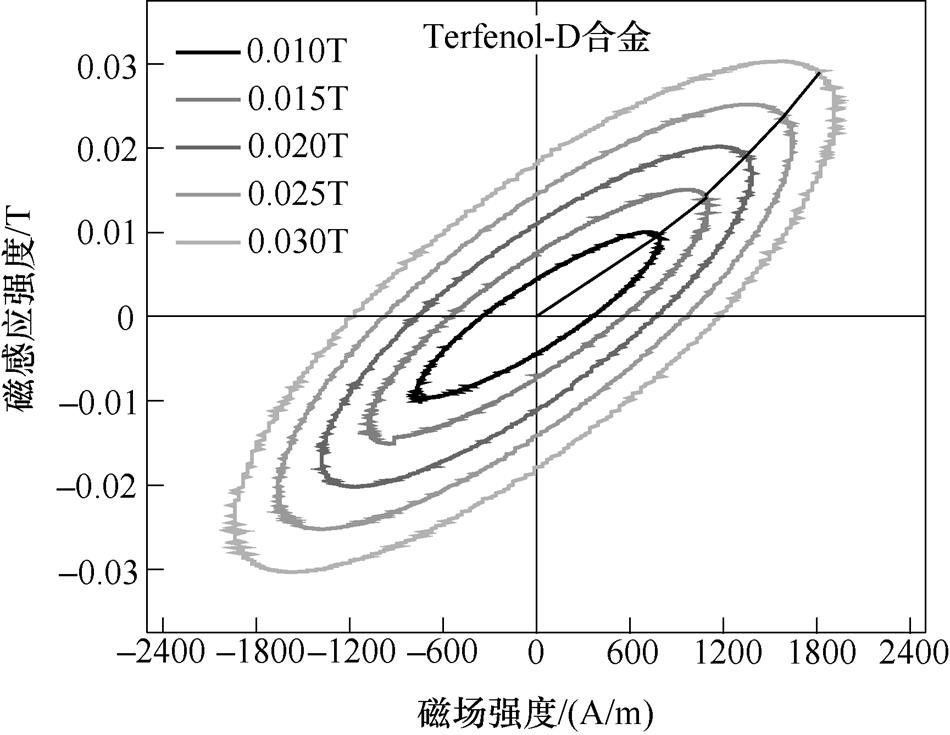
图4 Terfenol-D合金的动态磁滞回线
Fig.4 Dynamic hysteresis loops of Terfenol-D alloy
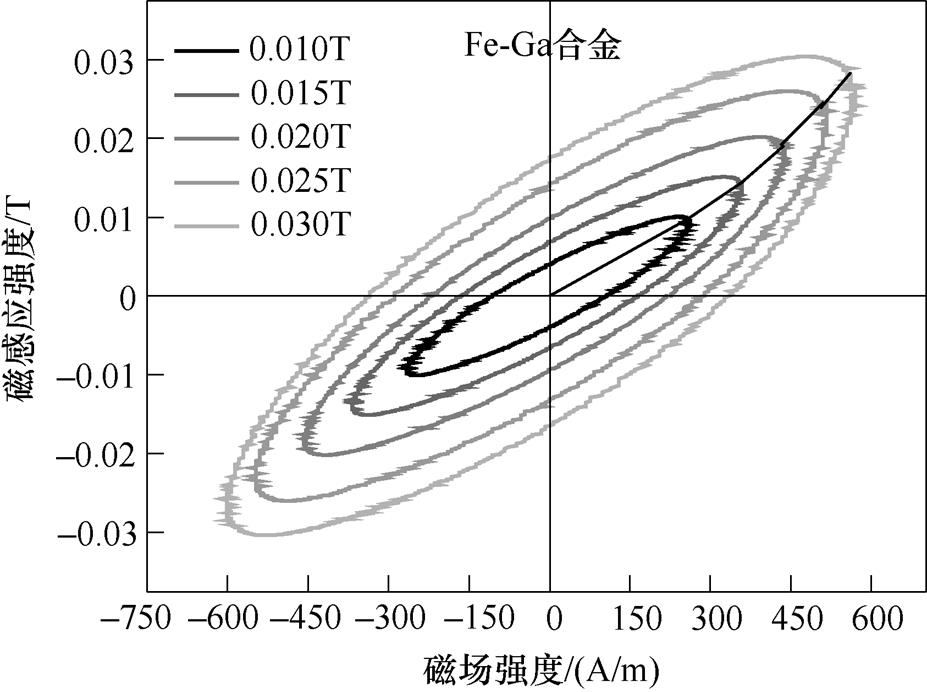
图5 Fe-Ga合金的动态磁滞回线
Fig.5 Dynamic hysteresis loops of Fe-Ga alloy
图6为利用图3～图5的实验结果得到三种样品的磁导率幅值与磁感应强度的关系。当磁感应强度的峰峰值在0.010～0.030T时，三种合金磁导率幅值都相应增加，Fe-Co-V、Terfenol-D和Fe-Ga合金的磁导率幅值分别增加了6.44%、21.57%和31.72%。Fe-Ga合金的磁导率增加最快，Fe-Co-V合金的磁导率幅值增加最慢。由式（13）可知，励磁磁场频率不变的情况下，磁场强度的增量小于磁感应强度的增量，实验结果得到三种样品的磁导率近似线性增加，三种合金材料的导磁性能不断提高，此磁化过程对应于基本磁化曲线的初始磁化阶段。结合式（15）可得到，相同磁感应强度情况下，Fe-Ga合金在动态磁化过程中的磁导率最大，磁能损耗相对其他两种合金较小；Terfenol-D合金的磁导率最小，其磁能损耗最大。在高频弱磁场下，随着磁感应强度的增大，促进合金内部更多的磁畴转动和磁畴壁移动，因此磁导率也逐渐增大。合金内部的原子磁矩在没有外磁场作用时在各个小区域内已经定向排列，在外界施加弱磁场时就显现出很强的导磁性。
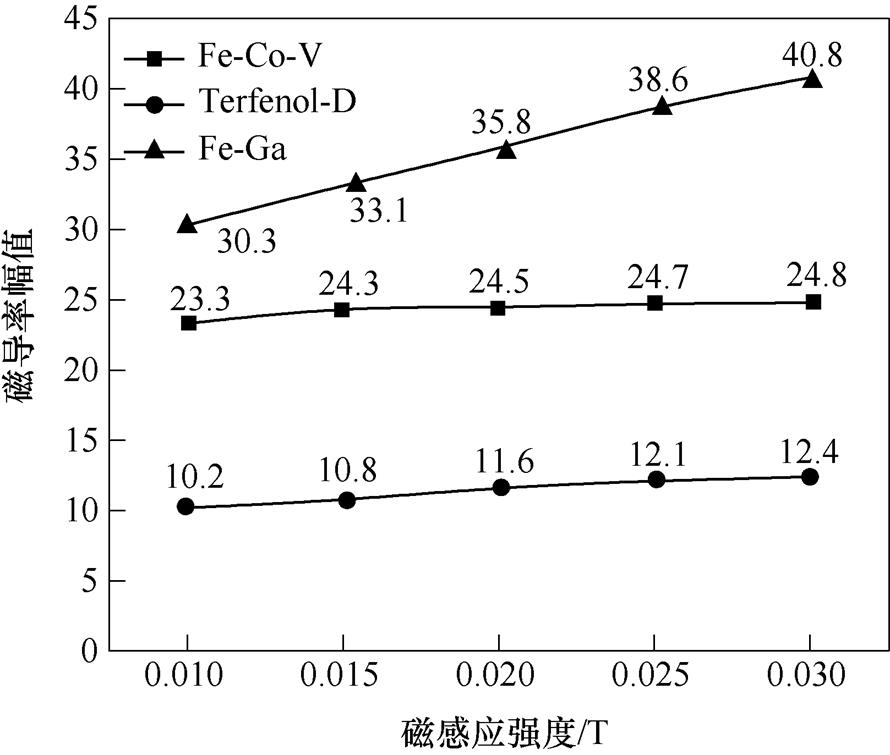
图6 不同材料的磁导率幅值随磁感应强度变化曲线
Fig.6 Variation curves of permeability amplitude with magnetic induction intensity for different materials
图7为从实验结果得到的三种合金介质损耗因数随磁感应强度的变化情况。图中，三种合金的损耗因数变化趋势代表了Fe-Co-V、Terfenol-D和Fe-Ga合金在磁感应强度的增大过程中，三种合金材料的损耗和储能的比值变化关系。分析可得，相同磁感应强度下，Fe-Co-V合金的损耗因数最大，Fe-Ga合金的最小。磁感应强度由0.010T变至0.030T时，Fe-Co-V合金的损耗因数变化波动较小，幅值较为稳定，因此该合金的电磁损耗和介质储能大小变化都较为均衡。而Terfenol-D合金和Fe-Ga合金的损耗因数都近似线性增加，分别增加了44%和59.52%。
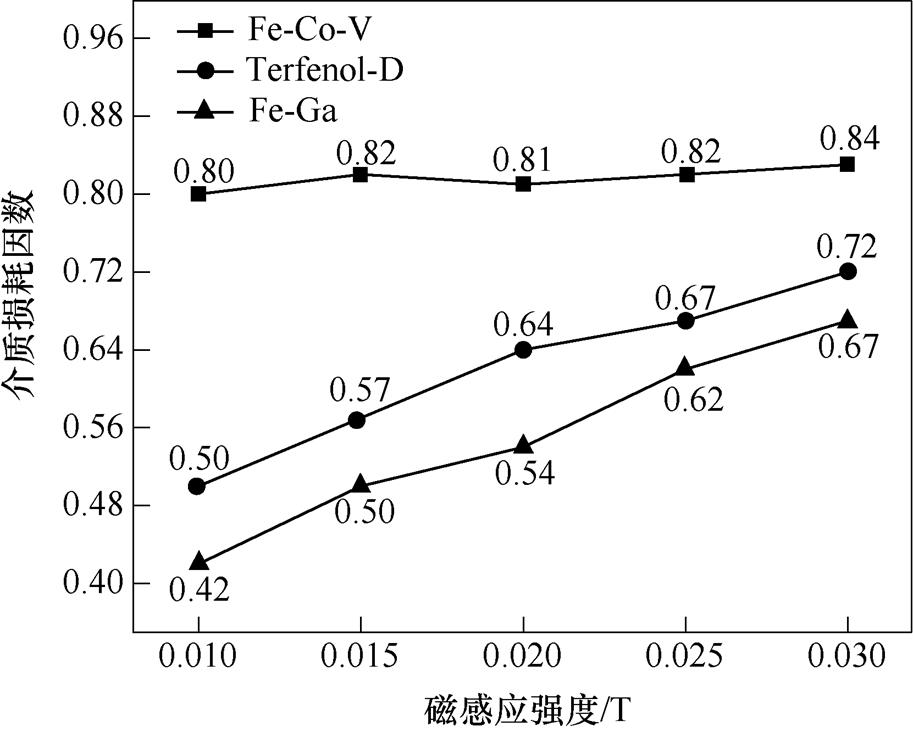
图7 不同材料的介质损耗因数随磁感应强度变化曲线
Fig.7 Loss factor curves of different materials with magnetic induction intensity
图8为实验结果和式（16）分析得到的三种样品的电磁损耗和磁感应强度的关系。在励磁磁场频率一定时，Fe-Co-V、Terfenol-D和Fe-Ga合金的电磁损耗分别增加了7.96倍、9.26倍和8.48倍。随着磁感应强度的增加，三种合金样品的电磁损耗都增大。在同一磁感应强度下，Terfenol-D合金的电磁损耗最大，Fe-Ga合金的电磁损耗最小。从微磁学角度分析，磁场的能量主要消耗在样品合金内部可逆磁畴壁之间移动和转动过程中的碰撞和摩擦，而磁畴自身吸收的能量主要转化为磁畴运动的动能，增加了磁畴运动速度，促进了磁畴在外加磁场的重新排列。
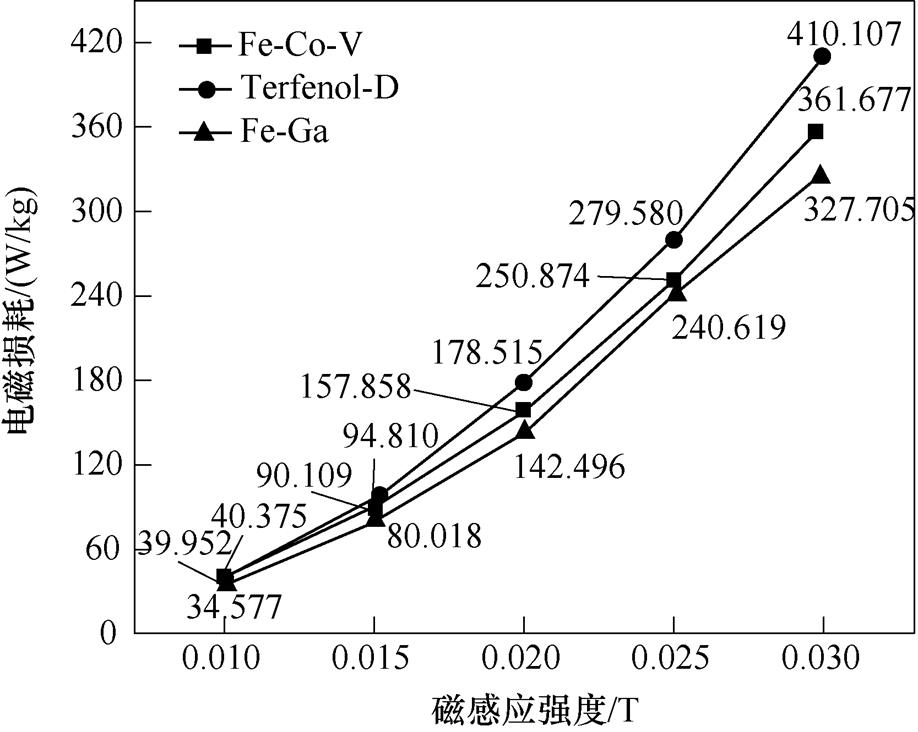
图8 不同材料的电磁损耗随磁感应强度变化曲线
Fig.8 Electromagnetic loss curves of different materials with magnetic induction intensity
图9～图11为最大磁感应强度为0.03T，励磁磁场频率分别为1kHz、10kHz、20kHz、30kHz、40kHz、50kHz、60kHz情况下测得的Fe-Co-V、Terfenol-D、Fe-Ga合金的动态磁滞回线。随着励磁磁场频率的增加，三种样品对应的椭圆形磁滞回环的倾斜程度都在增大，相应的椭圆环面积也增大，其中，Terfenol-D合金椭圆环倾斜程度增加最快，椭圆环的面积增加也最大。在励磁磁场频率为60kHz时，Terfenol-D合金所需要的励磁磁场强度最大，Fe-Ga合金所需的励磁磁场强度最小。另外，随着频率的增加，样品材料达到磁感应强度峰峰值0.03T所需的磁场强度也增加，相应的剩磁和矫顽力也在逐渐增大。为了促进磁致伸缩合金材料磁性介质中更多的磁畴转动和磁畴壁移动，也导致相应的电磁损耗增加，磁滞回环面积增大。
图9 Fe-Co-V合金的动态磁滞回线
Fig.9 Dynamic hysteresis loops of Fe-Co-V alloy
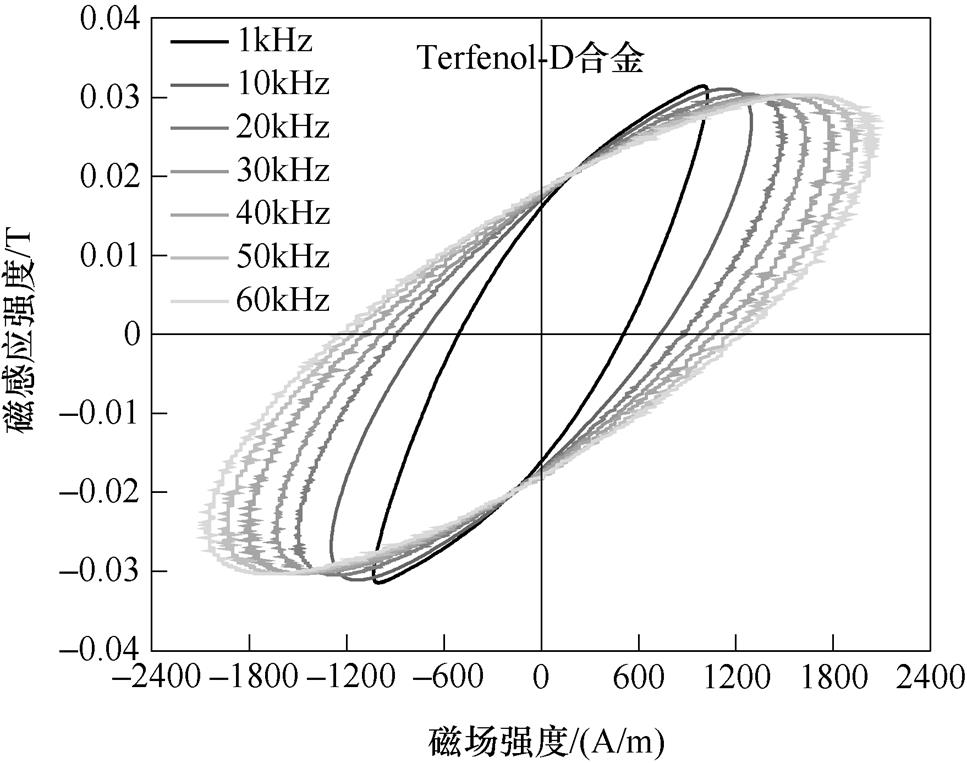
图10 Terfenol-D合金的动态磁滞回线
Fig.10 Dynamic hysteresis loops of Terfenol-D alloy
图12为利用图9～图11的实验结果得到的三种样品的磁导率幅值与频率的关系。励磁磁场频率为1～60kHz，Fe-Co-V、Fe-Ga合金磁导率幅值都是先增大后减小，有相似的磁导率变化特性，Terfenol- D合金的磁导率幅值逐渐减小后趋于平缓。相同励磁磁场频率下，Fe-Ga合金的磁导率幅值最大，Terfenol-D合金的最小。Fe-Co-V、Terfenol- D、Fe-Ga合金的磁导率幅值分别减小了30.06%、51.85%和14.76%，结合式（13），当磁感应强度一定时，随着励磁磁场频率增大，所需的磁场强度也在增大，对应的磁导率幅值逐渐减小。主要原因是励磁磁场频率越高，合金介质中磁畴转动和畴壁移动加剧，所需励磁磁场强度也越大。
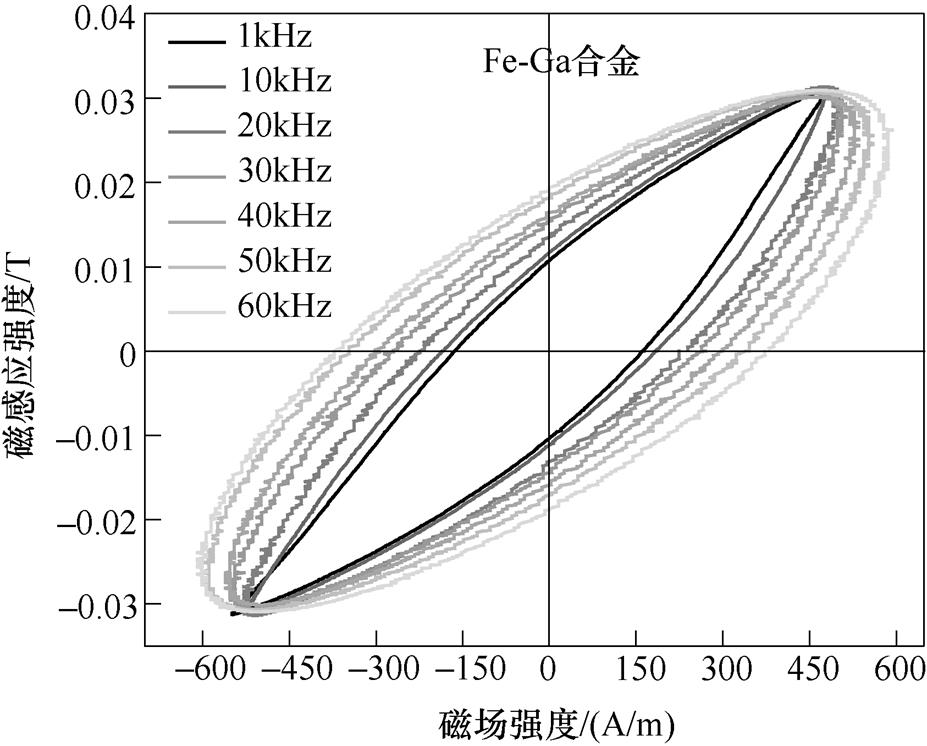
图11 Fe-Ga合金的动态磁滞回线
Fig.11 Dynamic hysteresis loops of Fe-Ga alloy
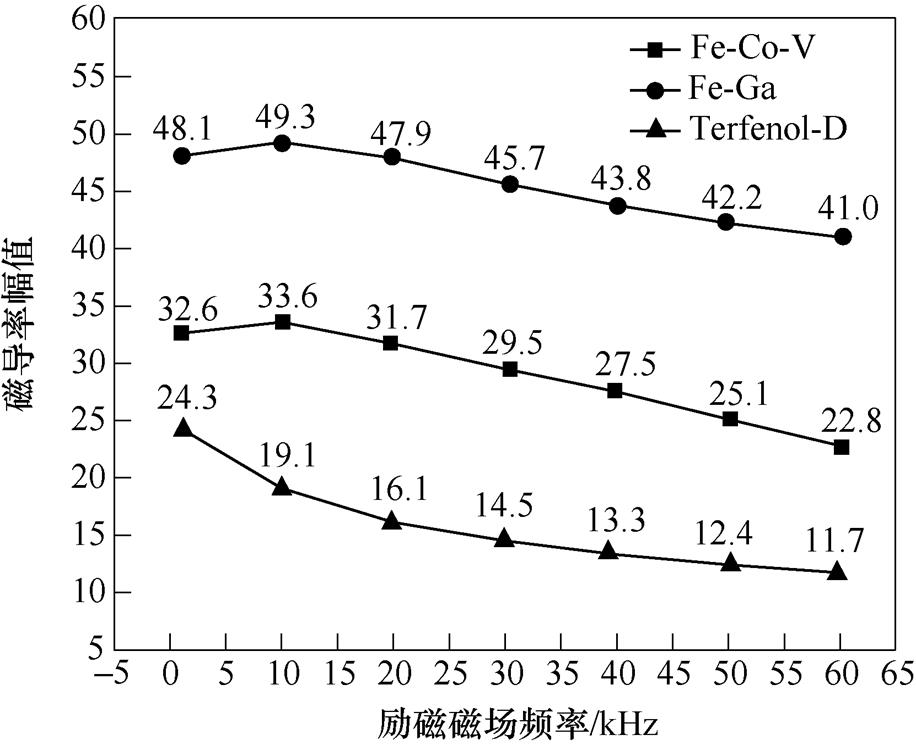
图12 不同材料的磁导率幅值随频率的变化曲线
Fig.12 Variation of permeability amplitude with frequency for different materials
由实验结果得到不同励磁磁场频率下的三种合金的介质损耗因数变化情况如图13所示，损耗因数表征了三种合金材料的损耗和存储能量的比值，损耗因数接近1时，代表材料中的能量存储和能量损耗接近相等。可以得到，随着励磁磁场频率的增加，Fe-Co-V合金和Fe-Ga合金的损耗因数都逐渐增大，分别增加了15.17倍和1.28倍，Terfenol-D合金的损耗因数先增大后趋于稳定，特别是在励磁磁场频率大于20kHz后，Terfenol-D合金的介质损耗因数波动较小，该合金的电磁损耗和介质储能在超声频率范围内变化较为均衡。
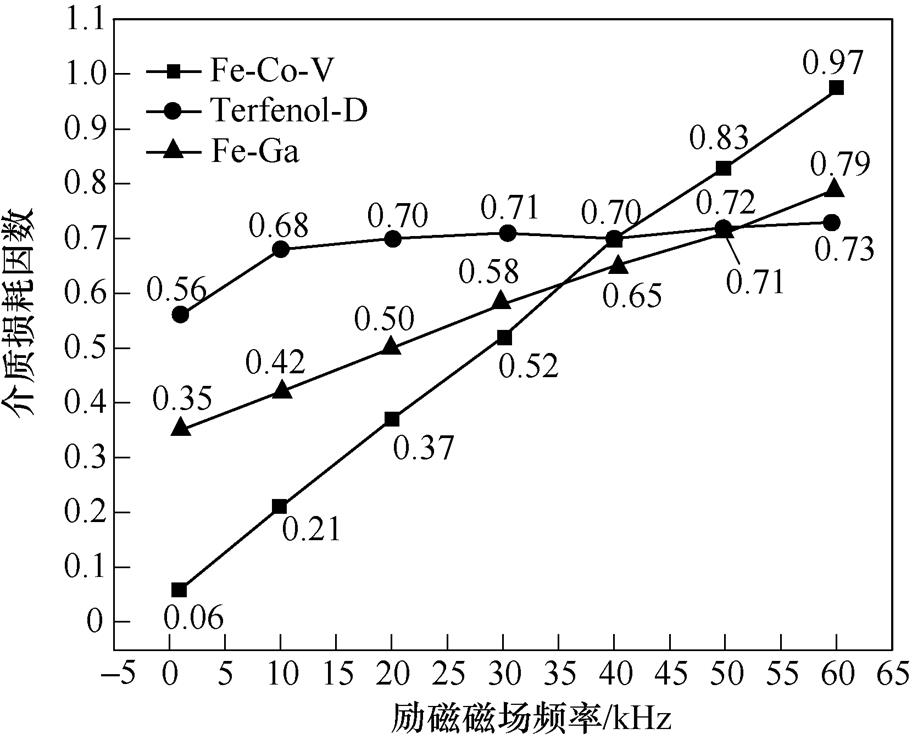
图13 不同材料的损耗因数随励磁磁场频率变化曲线
Fig.13 Loss factor curves of different materials with frequency of excitation magnetic field
图14为利用实验结果以及式（17）得到的三种环形合金样品的介质储能随频率变化的关系。励磁磁场频率由1～60kHz，Fe-Co-V、Terfenol-D和Fe- Ga合金的介质储能分别增加78.73倍、112.07倍和67.25倍，图14中，Terfenol-D合金的介质储能增加最快，Fe-Co-V合金的介质储能增加较慢。图15为利用图9～图11实验结果得到的三种环形样品电磁损耗与频率的关系。结合图15可以看出，随着励磁磁场频率的增加，三种材料的电磁损耗和介质储能均增加，但电磁损耗的增加幅度大于介质储能，也说明了励磁磁场频率的增加对材料的电磁损耗影响较大。
由图15可见，在相同磁感应强度0.03T时，随着励磁磁场频率的增加，三种合金样品的电磁损耗都增大。励磁磁场频率为1～20kHz时，Fe-Co-V、Terfenol-D和Fe-Ga合金的电磁损耗分别增加了152.03倍、33.59倍和29.39倍。可见在频率较低时，Fe-Co-V合金的电磁损耗增加较快，Fe-Ga合金增加较慢，同一频率下Terfenol-D合金的电磁损耗最大，Fe-Co-V合金的电磁损耗最小；当励磁磁场频率为20～60kHz的超声频率范围时，Fe-Co-V、Terfenol-D和Fe-Ga合金的电磁损耗分别增加了7.42倍、3.26倍和4.11倍。
图14 不同材料的介质储能随励磁磁场频率变化情况
Fig.14 Variation of dielectric energy storage of different materials with frequency of excitation magnetic field
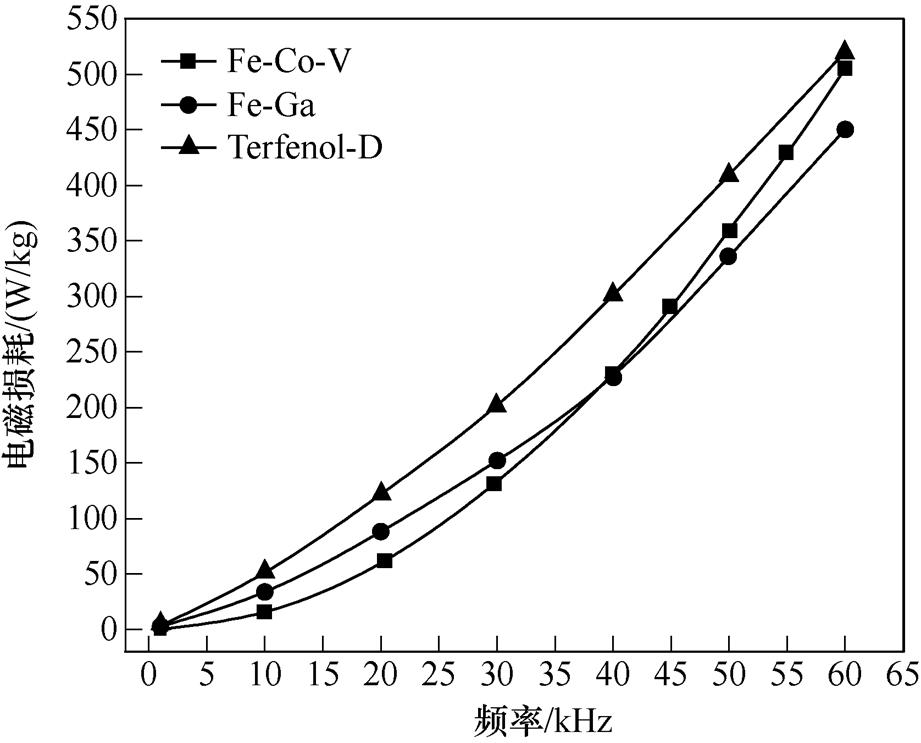
图15 不同材料电磁损耗与频率的关系
Fig.15 Relation between electromagnetic loss and frequency of different materials
整体来看，Terfenol-D合金的电磁损耗随频率增速最快且在同一频率下损耗最大。在1～40kHz内Fe-Ga合金的电磁损耗高于Fe-Co-V合金，而在40～60kHz内Fe-Ga合金电磁损耗低于Fe-Co-V合金。随着励磁磁场频率增加，损耗的增长量增加，可以得出损耗在低频的情况下，受频率影响小；在频率较高时，受频率影响大，幅值增加快。
1）当交变励磁磁场频率为50kHz，施加在样品上的磁感应强度为0.01～0.03T时，Fe-Co-V、Terfenol-D和Fe-Ga合金的磁导率分别增加了6.44%、21.57%和31.72%；Fe-Co-V合金的损耗因数变化波动较小，而Terfenol-D合金和Fe-Ga合金的损耗因数都近似线性增加，分别增加了44%和59.52%；Fe-Co-V、Terfenol-D和Fe-Ga合金的电磁损耗分别增加了7.96倍、9.26倍和8.48倍，在同一磁感应强度下，Terfenol-D合金的电磁损耗最大，Fe-Ga合金的电磁损耗最小。
2）在最大磁感应强度为0.03T，励磁磁场频率为1～60kHz时，Fe-Ga合金的磁导率最大，Terfenol- D合金的最小；Fe-Co-V合金和Fe-Ga合金的介质损耗因数都逐渐增大，Terfenol-D合金的介质损耗因数先增大后趋于稳定；Fe-Co-V、Terfenol-D和Fe-Ga合金的介质储能分别增加78.73倍、112.40倍和67.25倍；励磁磁场频率为1～20kHz时，Fe- Co-V、Terfenol-D和Fe-Ga合金的电磁损耗分别增加了152.03倍、33.59倍和29.39倍，Terfenol-D合金的电磁损耗最大，Fe-Co-V合金的电磁损耗最小；当励磁磁场频率为20～60kHz时，Fe-Co-V、Terfenol-D和Fe-Ga合金的电磁损耗分别增加了7.42倍、3.26倍和4.11倍。
参考文献
[1] 杨庆新, 李永建. 先进电工磁性材料特性与应用发展研究综述[J]. 电工技术学报, 2016, 31(20): 1-12.
Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1-12.
[2] Nguyen Y M, Bourrier D, Charlot S, et al. Soft ferrite cores characterization for integrated micro-inductors[J]. Journal of Micromechanics and Microengineering, 2014, 24(10): 104003.
[3] 胡伯平. 稀土永磁材料的现状与发展趋势[J]. 磁性材料及器件, 2014, 45(2): 66-77.
Hu Boping. Status and development tendency of rare-earth permanent magnet materials[J]. Journal of Magnetic Materials and Devices, 2014, 45(2): 66-77.
[4] Fackler S W, Alexandrakis V, König D, et al. Combinatorial study of Fe-Co-V hard magnetic thin films[J]. Science & Technology of Advanced Materials, 2017, 18(1): 231-238.
[5] 王伟旬, 陈远星, 刘志坚. 热处理工艺对新型铁钴钒磁滞合金性能和组织的影响[J]. 南方金属, 2016(3): 1-3.
Wang Weixun, Chen Yuanxing, Liu Zhijian. Effect of heat treatment on microstructure and properties of new Fe-Co-V magnetic hysteresis alloy[J]. Southern Metals, 2016(3): 1-3.
[6] Talebian S, Hojjat Y, Ghodsi M, et al. Study on classical and excess eddy currents losses of Terfenol- D[J]. Journal of Magnetism and Magnetic Materials, 2015, 388(6): 150-159.
[7] 黄文美, 薛胤龙, 王莉, 等. 考虑动态损耗的超磁致伸缩换能器的多场耦合模型[J]. 电工技术学报, 2016, 31(7): 173-178.
Huang Wenmei, Xue Yinlong, Wang Li, et al. Multi- field coupling model considering dynamic losses for giant magnetostrictive transducers[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 173-178.
[8] 卢诗华, 于歆杰, 楼国锋. 磁电层合大电流传感器的改进和性能分析[J]. 电工技术学报, 2017, 32(19): 94-99.
Lu Shihua, Yu Xinjie, Lou Guofeng. Modification and performance analysis on a magnetoelectric laminate based high-current sensor[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 94-99.
[9] 翁玲, 李薇娜, 曹晓宁, 等. 环形Fe-Ga合金动态磁导率和损耗分析[J]. 电工技术学报, 2019, 34(3): 459-465.
Weng ling, Li Weina, Cao Xiaoning, et al. Analysis of dynamic permeability and energy loss of ring- shaped Fe-Ga alloy[J]. Transactions of China Electro- technical Society, 2019, 34(3): 459-465.
[10] 翁玲, 罗柠, 张露予, 等. Fe-Ga合金磁特性测试装置的设计与实验[J]. 电工技术学报, 2015, 30(2): 237-241.
Weng Ling, Luo Ning, Zhang Luyu, et al. Design and experiment of a testing device for Fe-Ga magnetic properties[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 237-241.
[11] Weng Ling, Li Weina, Sun Ying, et al. High frequency characterization of Galfenol minor flux density loops[J]. AIP Advances, 2017, 7(5): 056023.
[12] Meng Hao, Zhang Tianli, Jiang Chengbao. Frequency dependence of loss behavior in bonded anisotropic giant magnetostrictive materials[J]. IEEE Transa- ctions on Magnetics, 2014, DOI: 10.1109/TMAG.2014. 2314282.
[13] Zhang Baoshan, Yuan Zhe, Zhao Hu, et al. Hysteretic behavior of the dynamic permeability in FeCoB thin films[J]. IEEE Transactions on Magnetics, 2016, DOI: 10.1109/TMAG.2015.2490139.
[14] 李立毅, 严柏平, 张成明. 驱动频率对超磁致伸缩致动器的损耗和温升特性的影响[J]. 中国电机工程学报, 2011,31(18): 124-129.
Li Liyi, Yan Baiping, Zhang Chengming. Influence of frequency on characteristic of loss and temperature in giant magnetostrictive actuator[J]. Proceedings of the CSEE, 2011, 31(18): 124-129.
[15] Li Yang, Zhu Lihua, Zhu Jianguo. Core loss calculation based on finite-element method with Jiles–Atherton dynamic hysteresis model[J]. IEEE Transactions on Magnetics, 2018, DOI: 10.1109/TMAG.2017.2765704.
[16] 李劲松, 杨庆新, 李永建, 等. 高频高磁密时叠置硅钢片的铁芯损耗计算式改进[J]. 高电压技术, 2016, 42(3): 994-1002.
Li Jinsong, Yang Qingxin, Li Yongjian, et al. Improved calculation formula of core losses for laminated silicon steels at high frequency and high flux density[J]. High Voltage Engineering, 2016, 42(3): 994-1002.
[17] Zhao Hanyu, Ragusa C, Appino C, et al. Energy losses in soft magnetic materials under symmetric and asymmetric induction waveforms[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(3): 2655-2665.
[18] 翁玲, 曹晓宁, 胡秀玉, 等. 双线圈铁镓合金换能器的输出特性[J]. 电工技术学报, 2018, 33(19): 62-71.
Weng Ling, Cao Xiaoning, Hu Xiuyu, et al. Output characteristics of double coil Fe-Ga alloy trans- ducer[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 62-71.
[19] Zhao Hanyu, Ragusa C, De La Barrière O, et al. Magnetic loss versus frequency in non-oriented steel sheets and its prediction: minor loops, PWM, and the limits of the analytical approach[J]. IEEE Transa- ctions on Magnetics, 2017, 53(11): 1-4.
[20] 韩赞东, 李晓阳. 基于动态磁化的结构钢磁导率和电磁损耗测量方法[J]. 清华大学学报: 自然科学版, 2014, 54(11): 1471-1474.
Han Zandong, Li Xiaoyang. Measurement of magnetic permeability and magnetic loss of structural steel for dynamic magnetization[J]. Journal of Tsinghua University: Science and Technology, 2014, 54(11): 1471-1474.
Analysis and Experimental Study on High Frequency Magnetostrictive Energy Loss of Different Magnetostrictive Materials
Abstract In this paper, the mathematical model of magnetic energy loss under small hysteresis loop is introduced. The high frequency hysteresis loops of Fe-Co-V, Terfenol-D and Fe-Ga alloy samples are measured by AMH-1M-S dynamic magnetic characteristic testing system. The experimental results and mathematical model were are used to compare and analyze the magnetic permeability amplitude, dielectric loss factor, dielectric energy storage and electromagnetic loss of the three materials. When the excitation magnetic field frequency is 50kHz, the dielectric loss factors of Terfenol-D and Fe-Ga alloys increases linearly with the increase of magnetic induction intensity, and the electromagnetic losses of all three alloys increases. When the magnetic induction intensity is 0.03T, the permeability amplitudes of Fe-Co-V and Fe-Ga alloys increases first and then decreases with the increase of the frequency of the excitation magnetic field. The dielectric energy storage of Terfenol-D alloys increases fastest and its electromagnetic loss increases fastest with the frequency. The electromagnetic loss of Fe-Ga alloy is higher than that of Fe-Co-V alloy in 1～40kHz and lower than that of Fe-Co-V alloy in 40～60kHz. The results of this paper provide a basis for electromagnetic loss analysis and high frequency device design of magnetostrictive materials.
keywords：High frequency, hysteresis loop, permeability, dielectric loss factor, electromagnetic loss
中图分类号：TM274
DOI: 10.19595/j.cnki.1000-6753.tces.190469
翁 玲 女，1978年生，博士，副教授，研究方向为新型磁性材料与智能器件。E-mail: llweng@163.com
黄文美 女，1970年生，博士，教授，博士生导师，研究方向为新型磁性材料与智能器件。E-mail: hzwm@hebut.edu.cn（通信作者）
国家自然科学基金项目（51777053）和河北省自然科学基金重点项目（E2017202035）资助。
收稿日期2019-04-21
改稿日期 2019-06-30
（编辑 崔文静）