0 引言
钢材广泛应用于航空航天、高铁制造、铁路轨道、机械加工等领域。由于钢板在制造过程中，原材料、制造设备、加工工艺等多种因素造成金属内部产生裂纹、分层、夹渣、腐蚀等各种缺陷。这些缺陷的存在会使钢结构的使用寿命、强度以及稳定性能急剧下降。因此对钢板缺陷的检测和识别意义重大[1]。
电磁超声换能器（Electromagnetic Acoustic Transducer, EMAT）以电磁耦合的方式可以方便地激发各种类型的超声波，其中，体波可以很好地检测试件内部缺陷，但对表面及近表面缺陷存在检测盲区，而表面波在传播时其能量主要集中在试件表面下一个波长的深度，适用于厚板的表面开口检测，可以实现对表面裂纹的检测[2]。沈阳工业大学的杨理践建立三维电磁超声表面波有限元模型，探究了EMAT产生表面波的机理，得出表面波的位移与激励电流成正比[3]。南昌航空大学的时亚建立了多根分裂曲折线圈接收 EMAT的有限元模型，分析了曲折线圈导线宽度、高度和根数以及永磁铁尺寸、提离距离对接收电压信号幅值的影响规律[4]。目前，对电磁超声表面波模型的研究较多，但材料特性对电磁超声表面波的影响鲜有研究，因此本文在考虑到铁磁材料特性对表面波影响的基础上建立更加精确的电磁超声表面波模型，分析表面波的传播特性。
目前国内外学者对铁磁性材料的检测许多基于压电超声换能器。英国焊接研究所的 Y. Gharaibeh使用 Abaqus建立了钢轨的有限元模型，并分析了钢轨的频散特性，得到了适合检测该型钢轨各个部分缺陷的导波模态和频率，成功检测到了轨头和轨底边缘处深度分别为2mm和5mm的横向缺陷[5]。香港理工大学的 Yifei Pei利用压电超声探头得到铁路道岔有裂纹和无裂纹的时域图，开发了信号处理算法，利用该算法自动区分正常轨道和裂缝[6]。压电超声换能器属于接触式传感器，在使用过程中耦合剂限制了压电传感器的适用场合和检测效率。而电磁超声检测技术具有非接触、无需耦合剂、重复性好等特点[7-8]，还可以激发较高频率导波。超声导波直接在钢板中激发，能够实现较小缺陷的探伤[9-10]。钢板是铁磁性材料，与非铁磁性材料不同的是，换能过程中增加了磁致伸缩效应和磁化效应。偏置磁场的饱和程度对铁磁材料的换能机制主导作用影响巨大。通过仿真分析得到在弱磁场情况下，磁致伸缩效应由磁畴壁移占主导作用；在磁场饱和时，磁化由磁畴转矩引起，应变会减小，而磁感应强度不再变化，磁致伸缩引起的应变几乎不再改变[11-14]。R. Ribichini利用试验对不同等级的钢管进行检测，评估EMAT的转换机制对材料的依赖性，得出洛伦兹力对钢材料的物理性质不太敏感，当材料中存在高磁致伸缩氧化物时，磁致伸缩力会变得显著。因此磁致伸缩效应比洛伦兹力对材料的特性更敏感[15]。Soon-Woo Han讨论了非接触式电磁超声导轨检测技术，并通过有限元模型进行模拟，确定最适合缺陷检测的工作频率，检测出钢轨内部和表面的损伤[16]。由于EMAT的信噪比相对较低，EMAT的性能在很大程度上取决于试件的特性，需要进一步建立更加精确的铁磁材料EMAT模型，研究铁磁材料EMAT的换能机制，特别是解耦和量化EMAT中固有的转换力[17-18]。
关于对缺陷的定量检测，文献[19]在已知入射波的情况下，根据裂纹两侧区域的位移和内力的连续性条件得到了反射波和透射波的幅值系数，分析了入射振动波通过圆柱壳体裂纹后的透射、反射系数与激励频率和裂纹尺寸之间的关系；文献[20]通过研究二维矩形凹口对 Lamb波的反射系数和透射系数，以快速检查结构中缺陷的宽度和深度；文献[21]利用反射系数及接收 Lamb波之间的时间差对铝管裂纹进行定量检测。针对现有文献中缺陷定量检测对技术人员的依赖，本文通过对模型建立方法的改进，提高表面波对缺陷定量检测的效率和精度。
表面波适用于检测厚板开口缺陷，本文基于磁致伸缩机理、洛伦兹力机理和磁化力机理，利用有限元软件 COMSOL建立完整的铁磁材料电磁超声表面波模型。通过仿真分析表面波对钢板槽型缺陷的响应特性，研究不同缺陷深度与反射系数、透射系数的关系，得到拟合函数，并对不同深度的缺陷进行实验检测。
1 铁磁材料的电磁超声表面波换能器理论
电磁超声表面波换能器的模型如图1所示。
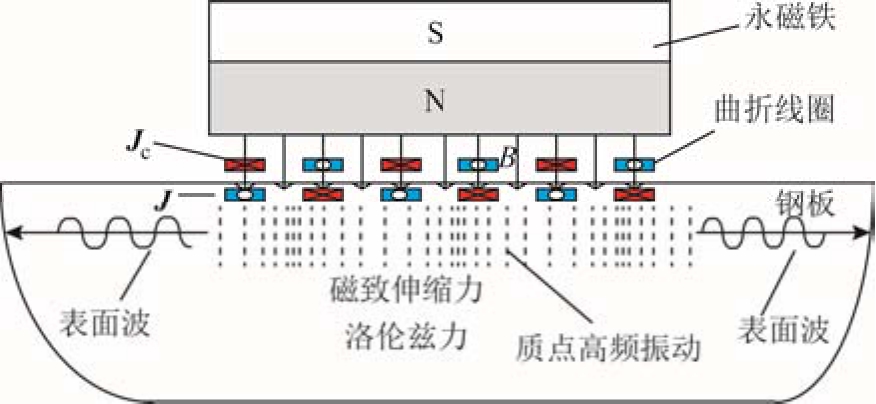
图1 电磁超声表面波换能器模型示意图
Fig.1 Schematic diagram of electromagnetic acoustic surface wave transducer
永磁体提供静态偏置磁场Bs；线圈中通入高频交变电流时，该电流将在导体周围产生交变磁场Bd，在交变磁场的作用下，导体趋肤深度内将产生感应涡流 J，铁磁材料中的电涡流密度分为洛伦兹力电流密度Je和磁致伸缩电流密度JM，其中
式中，A为矢量磁位；γ为材料的电导率；Bm为逆磁致伸缩感生出的磁感应强度；∇为梯度算子。洛伦兹力电流密度Je在磁场作用下产生的洛伦兹力为
对于磁致伸缩材料，磁致伸缩本构关系可以表示为
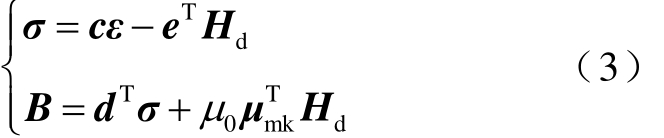
式中，ε为应变矩阵；σ为应力张量矩阵；
为材料的可逆磁导率矩阵；0μ为真空磁导率；Hd为动态磁场强度；B为静态应力下板中的总磁感应强度；d为压磁矩阵；c为刚度矩阵；eT为逆压磁矩阵。式（3）中第一个方程描述了磁致伸缩效应，即施加磁场引起的应变；第二个方程描述了逆磁致伸缩效应，即当应力作用产生磁通变化时，就可以通过传感器检测到磁通密度的变化。在大偏置磁场作用下（Hs>>Hd），由铁磁材料的特性出发，可以从磁致伸缩应变曲线和施加的偏置磁场 Hs中导出压磁矩阵d的所有分量。由应力产生的磁感应强度相对总的磁通密度较小，因此 T d σ可以忽略。
建立磁致伸缩模型需要对本构方程进行修正。由于EMAT中静态磁场远大于动态磁场，材料的压磁矩阵可表示为
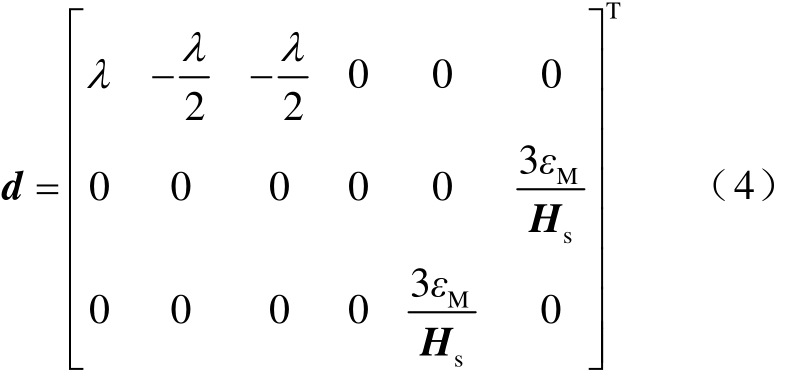
式中，λ、εM、Hs分别为材料的磁致伸缩系数、磁致伸缩应变和偏置磁场强度。在多晶体铁磁性材料中，材料的磁致伸缩特性可以和压电材料的压电特性近似。从压磁矩阵中得出有两个独立的系数分别为λ和
，因此动态磁致伸缩应变可以用这两个系数表示。
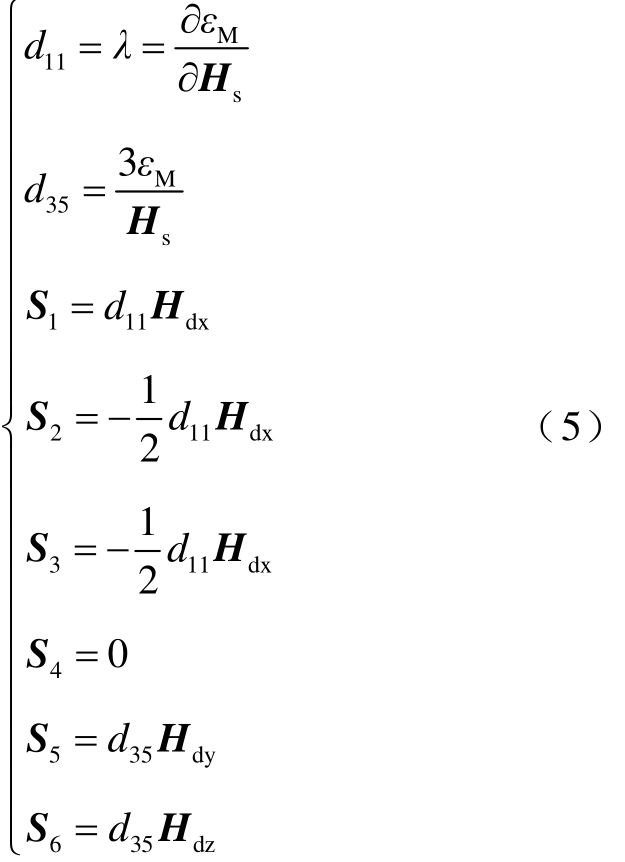
式中，d11和d35为两个独立的压磁系数，其中d11与应变的大小有关，而d35与应变的方向变化有关。偏置磁场在一定程度上产生磁应变，而动态磁场使应变在静磁致伸缩应变附近振荡。S1~S6为被测试件内部动态磁致伸缩应变。由文献[22]通过桥式应变测量设备得到低碳钢的磁致伸缩曲线如图2所示。由式（5）可以计算得到压磁系数d11和d35，如图3所示。显然，由于压磁系数是非线性参数，由 EMAT产生的磁致伸缩应变是偏置磁场的非线性函数。
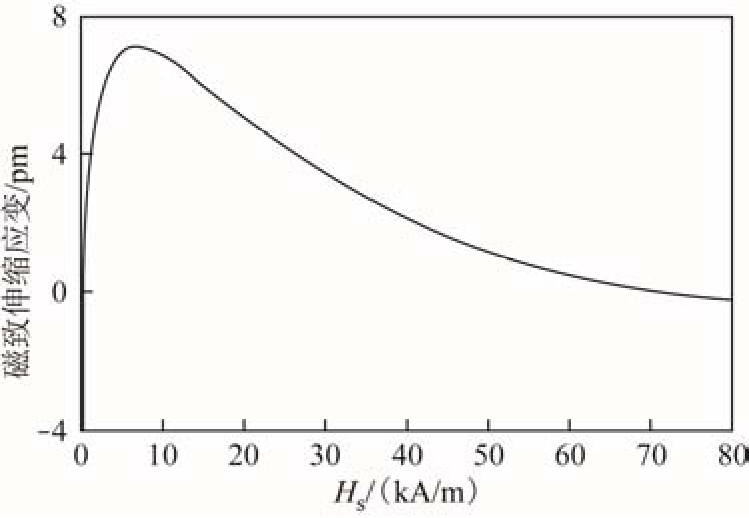
图2 低碳钢的磁致伸缩曲线
Fig.2 Magnetostrictive curve of a low carbon steel
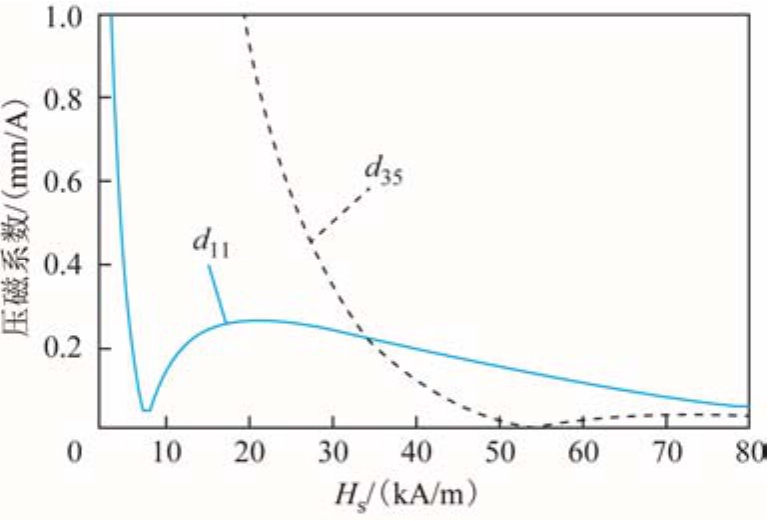
图3 压磁系数d11和d35的绝对值
Fig.3 Absolute value of the magnetostriction coefficient d11 and d35
磁致伸缩力的大小与动态磁场强度 Hd和逆变压磁矩阵eT相关，磁致伸缩力的表达式为
激励线圈中通入高频电流时产生交变的动态磁场，动态磁场和磁化矢量相互作用致使材料磁距排列趋于一致进而产生磁化力FM为
式中，M为磁化强度。磁化力作用于试件内部的晶格，使其相互作用产生应力波。
在铁磁材料中，质点所受的力为洛伦兹力、磁化力和磁致伸缩力的合力。一般情况下，铁磁材料中磁致伸缩力比磁化力要大六个数量级，因此磁化力在电磁介质上的作用可以忽略不计。
2 电磁超声表面波的缺陷检测特性分析
本文采用COMSOL Multiphysics有限元仿真软件建立电磁超声表面波仿真模型，分为三个阶段:①建立几何模型。在钢板左右两界面施加低反射边界条件，忽略结构边界的反射。钢板自身的特性通过对材料模块进行加载。考虑到网格剖分对计算精度的影响，对空气区域网格剖分加粗、对钢板的趋肤效应区域进行三层以上的网格剖分。②建立电磁场模型。铁磁材料不同之处在于需要将由于磁化和聚磁作用产生的附加磁场添加在安培定则里。对瞬态求解的步长及相对误差进行适当的选取，以保证求解计算的正确性和稳定性。③表面波声场模型建立。在固体力学模块中，洛伦兹力和磁化力通过公式添加，而固有的磁致伸缩力则依据铁磁材料的本构方程将其转变为应变添加在体载荷中，实现由磁场向力场的转变。换能器的工作过程就是由 EMAT实现电场-磁场-力场的能量转换。
2.1 电磁超声表面波有限元模型建立
钢板的宽×高为300mm×50mm；产生静态磁场的磁铁的宽×高为 36mm×10mm；磁铁与钢板的距离为1mm；导线的宽×高为0.6mm×0.2mm，其提离距离为0.3mm；采用表面波波长为9mm，当线圈间距为波长的一半时激发表面波的幅值最大，因此线间距为4.5mm，根据表面波在钢板中的传播速度为2 964m/s，计算得到频率为0.33MHz。钢板电磁超声表面波仿真模型如图 4所示。缺陷两侧质点1(50,-1)和质点2(170,-1)为观察点。
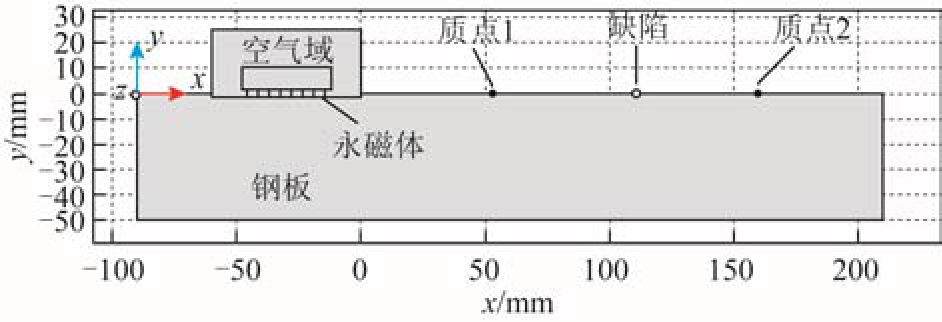
图4 钢板中电磁超声表面波仿真模型
Fig.4 Electromagnetic acoustic surface wave simulation model in steel plate
曲折线圈通入经过高斯窗调制的正弦函数i(t)，其表达式为
式中，Imax为激励电流幅值；α为带宽系数；τ为时间常数；f为脉冲中心频率。
铁磁材料在外磁场作用下由于磁化和聚磁作用会产生附加磁场，故附加磁场需通过磁化曲线（见图5）添加到安培定则里。
静磁感应强度和动磁感应强度与涡流密度相互作用产生洛伦兹力，即式（2），通过体载荷加载到试件的特性。对于磁致伸缩应力，则将其转换为应变添加在固体力学，将压磁矩阵中涉及的两个变量d11、d35转换为六个应变量S1~S6添加在固体力学中。
图5 低碳钢磁化曲线
Fig.5 The magnetization curve of low carbon steel
2.2 电磁场仿真分析
基于以上分析建立钢板电磁超声表面波有限元模型，采用稳态求解计算偏置磁场的分布，如图6所示。因铁磁材料的磁化作用产生了附加磁场，故与非铁磁性材料相比，永磁体提供的静态偏置磁场并非近似均匀的磁场。通有高频交变电流的线圈产生的动态磁场分布如图7所示，动态磁场从线圈中心到边缘逐渐减弱。高频电流和磁场耦合在钢板中感应出涡流，钢板中的涡流密度分布如图8所示。因电流在相邻线圈的幅值相同、方向相反，故产生的涡流幅值相同、方向相反。涡流主要集中在趋肤层，随钢板深度增加而迅速减小。各匝线圈正下方的涡流密度最强，超出线圈边缘逐渐减弱。
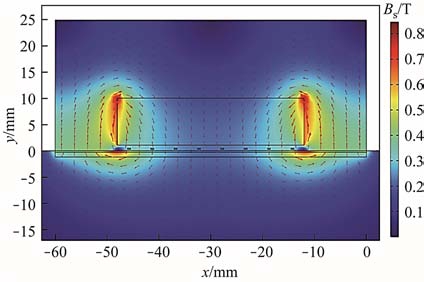
图6 永磁铁产生的偏置磁场分布
Fig.6 The distribution of bias magnetic field generated by permanent magnets
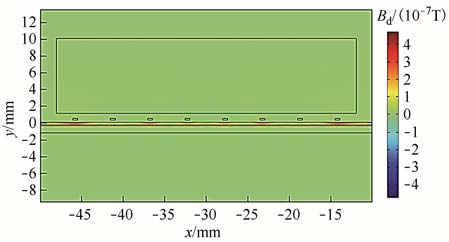
图7 线圈产生的磁场分布
Fig.7 Magnetic field distribution generated by the coil
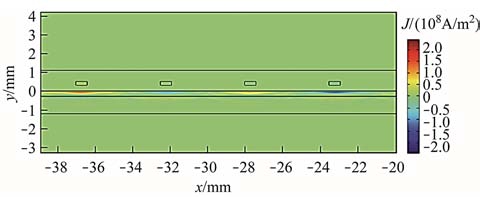
图8 钢板中涡流密度分布
Fig.8 The distribution of eddy current density in the steel plate
2.3 声场仿真分析
钢板中表面波的传播过程如图 9所示。激发的波沿表面传播，可以检测试件表面的缺陷。表面波在传播过程中模式比较纯净，当经过缺陷时，只有少数向下传播的体波，很少发生波束转换，无频散和多模态现象。随着传播时间的增加，表面波位移衰减较慢，而体波位移则衰减较快。质点1先接收到直达波，当表面波经过缺陷作用后，一部分反射回来的波再次经过质点 1，质点 1接收到反射波；另外一部分经过质点2，质点2主要接收透射波。
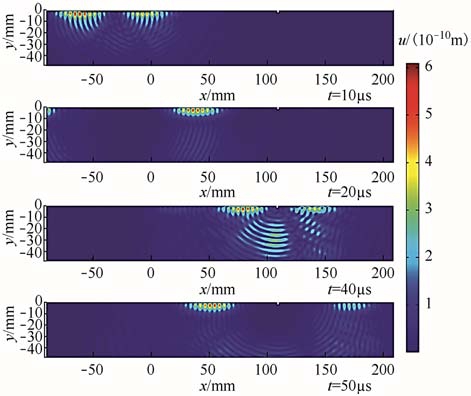
图9 曲折线圈EMAT在钢板中产生的表面波位移
Fig.9 Surface displacement in steel plate generated by meander coil EMAT
2.4 表面波缺陷检测特性分析
取缺陷两侧质点 1(50,-1)和质点 2(170,-1)为观察点，从时域进行质点位移分析，如图10所示。图10a为质点1接收的波形，主要接收反射波；图10b为质点2接受的波形，主要接收透射波。
图10 有缺陷时表面波的响应特性
Fig.10 Response characteristics of surface waves in the presence of defects
图10 a中第一个波包为直达波，幅值为3.121×10-8mm；第二个波包为经过缺陷反射回来的反射波，可以明显地看出直达波强于反射波，对反射波进行分析可以得到缺陷的特征。图10b第一个波包为穿过缺陷的透射波，幅值为 -9 9.782 10×mm，透射波比图10a中直达波的幅值小，一部分是由于缺陷的作用，另一部分是表面波向垂直于钢板方向传播体波的结果。在钢板中，槽型裂纹类缺陷大小和深度对反射波和透射波的幅值影响很大。本文研究缺陷深度变化对表面波传播情况的影响。为表征反射波和透射波的大小，可用反射系数R与透射系数T做对比。
2.5 缺陷深度与反射系数、透射系数之间的关系
仿真时采用波长9mm的表面波，能够在钢板表面下的一个波长内实现对缺陷的检测。建立不同深度的二维矩形槽缺陷几何模型，在相同的激励条件下，仿真模型只改变缺陷的深度，在缺陷的两侧质点1和质点2处进行测量，将缺陷深度进行参数化扫描得到反射系数和透射系数随缺陷深度的变化曲线，如图11所示。
图11 反射系数、透射系数随缺陷深度变化曲线
Fig.11 Reflection and transmission curves versus flaw depth
如图11a所示，反射系数随缺陷深度的增加而呈上升趋势。当缺陷相比于波长较小时，反射波也较小，说明表面波很容易从较浅的缺陷透射过去；当缺陷深度增加到半波长时，反射波的增长速度很快，说明缺陷越深，越容易将表面波反射回来；当缺陷的深度达到一个波长时，反射系数基本不再增长。
如图11b所示，透射波随缺陷深度的增加呈下降趋势。在缺陷深度小于半波长时，透射波急剧下降；大于半波长时，下降缓慢，甚至在一个波长之后呈现稳定的趋势。
通过对比反射系数和透射系数，可以看出反射系数和透射系数与缺陷深度都呈现单值函数，而反射系数对于接近半波长深度的缺陷更敏感，因此选取反射系数进行曲线拟合。以反射系数x为自变量，缺陷深度与波长之比y为变量，进行拟合。
选用线性拟合和多项式（三阶多项式、四阶多项式）分别对离散点进行拟合并得到相应的拟合函数。从图 12可以看出线性拟合与其他两种方法相比，离散点并没有更多地落在拟合线上，拟合效果稍差。进一步对三阶和四阶多项式拟合的残差模进行比较，三阶残差模为 0.081 309，四阶残差模为0.074 048。可以看出当阶数由三阶增加到四阶时，残差减小的幅度并不大，因此再增加阶数拟合的效果不会有很大的成效，并且增加阶数会降低拟合精度。综合考虑，选用三阶拟合函数作为拟合的结果。拟合的曲线表达式为
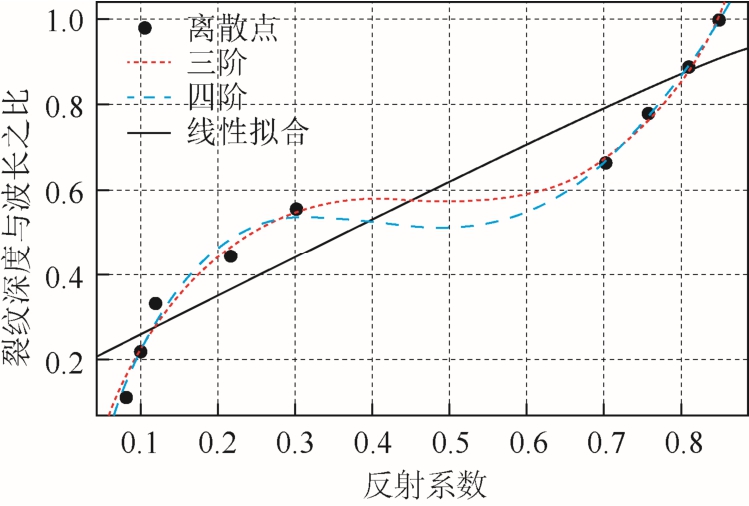
图12 裂纹深度与反射系数拟合曲线
Fig.12 The fitting curves of flaw depth with reflection coefficient
从图 12可以看出，三阶拟合结果与离散点很好地反映了裂纹深度与反射系数之间的函数关系，因此可以将此拟合函数作为量化裂纹深度的一个依据。
3 缺陷检测实验结果与分析
对 H-80标准钢板裂纹试块进行分析，标准试块中存在三处裂纹，裂纹深度分别为0.5mm、1.0mm、1.5mm，裂纹缺陷具体信息如图13所示。由于试块相对比较短，导致缺陷回波和边界回波叠加在一起，增加了分析的难度，所以采用单方向表面波EMAT。利用 Ritec RAM-5000的双输出通道和输出延迟功能产生相位差90°的1MHz信号，作用于线圈，使EMAT 产生单方向的表面波，这样可以避免一侧边界回波的干扰。
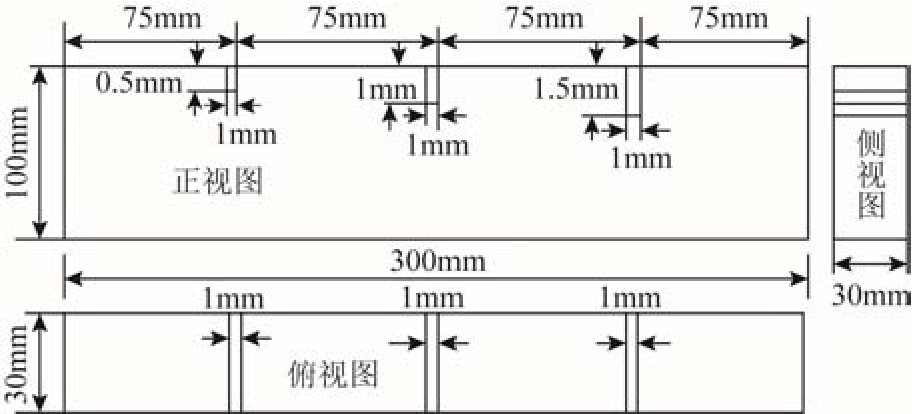
图13 标准裂纹试块
Fig.13 Standard crack test block
首先对长×宽分别为 300mm×100mm的完好钢板使用单方向表面波进行检测，采用一发一收的方式进行实验。激发端距离左侧端面为175mm，接收端距离右侧端面为 25mm，得到的波形如图 14所示，从激发端到右端面回波，传播的距离为150mm，传播的时间为49.7μs（传播时间为主冲击的峰峰值所对应的时刻与反射回波峰峰值所对应的时刻的差值），可以计算得到钢板中表面波的传播速度为3 012m/s，与理论波速的误差为1.7%。
图14 无缺陷时接收电压的波形
Fig.14 The terminal voltage without crack defects
为研究裂纹深度对表面波传播情况的影响，分别对H-80标准裂纹试块三处裂纹进行反射波实验，采用一发一收的方式进行实验，得到不同缺陷的反射波幅值，计算出反射系数，进而利用裂纹深度与反射系数曲线可估算出缺陷深度，裂纹容量分析结果见表1。
表1 裂纹定量分析结果
Tab.1 The results of quantitative analysis of crack
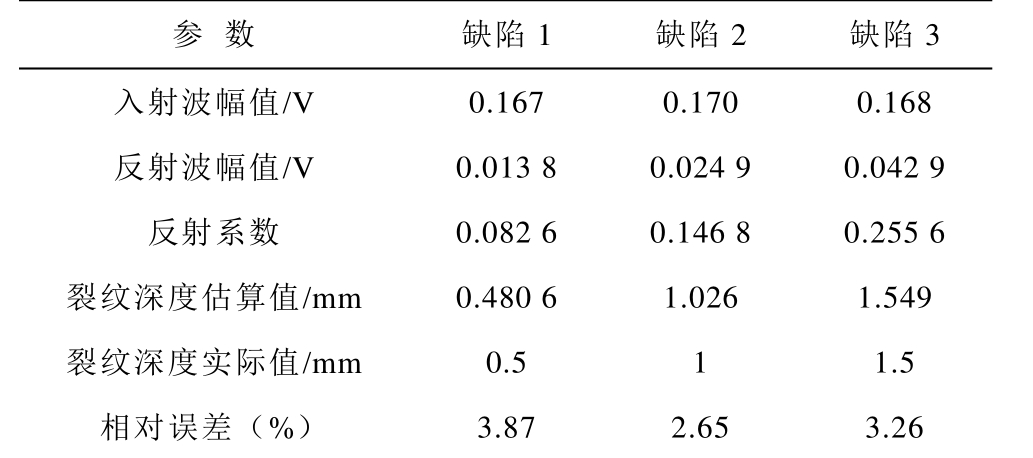
参 数 缺陷1 缺陷2 缺陷3入射波幅值/V 0.167 0.170 0.168反射波幅值/V 0.013 8 0.024 9 0.042 9反射系数 0.082 6 0.146 8 0.255 6裂纹深度估算值/mm 0.480 6 1.026 1.549裂纹深度实际值/mm 0.5 1 1.5相对误差（%） 3.87 2.65 3.26
同理，对 H-81钢板标准裂纹试块（此标准试块中三处裂纹缺陷的深度分别为2mm、3mm、4mm）进行反射波实验，通过反射系数可以估算出各缺陷深度。将 H-80、H-81试块缺陷的实际值和估算值进行对比，如图15所示。
通过计算表面波的反射系数与裂纹深度之间的关系，能够有效地检测出铁磁性材料裂纹缺陷的深度。由于测量结果的读取误差以及铁磁材料实际参数与仿真模型的误差，使得其裂纹深度的定量检测存在一定的误差。
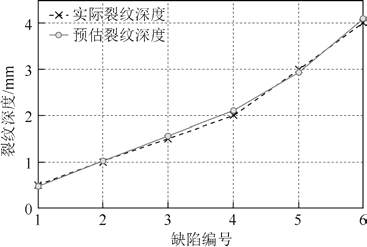
图15 实际裂纹深度和估算裂纹深度对比
Fig.15 The comparison of actual crack depth and estimated crack depth
4 结论
依据铁磁材料的电磁特性以及本构方程对钢板电磁超声表面波换能器的换能机制进行了解耦和量化。通过有限元建模和仿真分析，研究了钢板上磁感应强度和涡流密度的分布规律以及表面波的传播特性，并得到了钢板缺陷深度、波长之比和反射系数之间的关系。最后对标准裂纹试块进行了实验验证，结果表明通过反射系数能够定量检测钢板裂纹纵向深度，为铁磁材料的缺陷定量检测奠定了基础。
[1] Reddy K A. Evaluation of stainless steel materials[J].Materials Today Proceedings, 2017, 4(8): 7302-7312.
[2] Kang Lei, Zhang Chao, Dixon S, et al. Enhancement of ultrasonic signal using a new design of Rayleighwave electromagnetic acoustic transducer[J]. NDT &E International, 2017, 86: 36-43.
[3] Yang Lijian, Li Chunhua, Liu Mingming, et al.Simulation and analysis of surface wave based on finite element method[C]//Fifth International Conference on Intelligent Networks & Intelligent Systems, Tianjin,China, 2012: 209-212.
[4] 时亚, 石文泽, 陈果, 等. 钢轨踏面检测电磁超声表面波换能器优化设计[J]. 仪器仪表学报, 2018,39(8): 239-249.Shi Ya, Shi Wenze, Chen Guo, et al. Optimized design of surface wave electromagnetic acoustic transducer for rail tread testing[J]. Chinese Journal of Scientific Instrument, 2018, 39(8): 239-249.
[5] Gharaibeh Y, Sanderson R, Mudge P, et al.Investigation of the behaviour of selected ultrasonic guided wave modes to inspect rails for long-range testing and monitoring[J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit, 2011, 1(3): 1-14.
[6] Pei Yifei. Crack detection of railway turnouts using piezoelectric sensors[D]. Hong Kong: The Hong Kong Polytechnic University, 2014.
[7] Jian Xiaoming, Dixon S, Edwards R S, et al. Coupling mechanism of an EMAT[J]. Ultrasonics, 2006, 44(8):653-656.
[8] 吕敬祥, 刘国强. 磁声电无损检测及改进的 EMD消噪方法[J]. 电工技术学报, 2018, 33(17): 3935-3942.Lü Jingxiang, Liu Guoqiang. Magneto-acoustoelectrical NDT and improved EMD de-noising algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3935-3942.
[9] Edwards R S, Dixon S, Jian X. Characterisation of defects in the railhead using ultrasonic surface waves[J]. NDT & E International, 2006, 39(6): 468-475.
[10] 翟国富, 梁宝, 贾文斌, 等 .骨架型电磁超声相控阵换能器设计[J]. 中国电机工程学报, 2018, 29(1):1-7.Zhai Guofu, Liang Bao, Jia Wenbin, et al. Design of skeleton-type electromagnetic ultrasonic phased array transducer[J]. Proceedings of the CSEE, 2018, 29(1):1-7.
[11] Seher M, Nagy P B. On the separation of lorentz and magnetization forces in the transduction mechanism of Electromagnetic acoustic transducers (EMATs)[J].NDT & E International, 2016, 84: 1-10.
[12] Kim H J, Ju S L, Kim H W, et al. Numerical simulation of guided waves using equivalent source model of magnetostrictive patch transducers[J]. Smart Materials& Structures, 2015, 24(24): 15006-15023.
[13] 金亮, 寇晓斐, 郭富坤, 等. 基于电磁超声换能器的铁磁材料电磁声发射检测方法[J]. 电工技术学报, 2017, 32(18): 98-105.Jin Liang, Kou Xiaofei, Guo Fukun, et al.Electromagnetic acoustic emission detection method of ferromagnetic materials based on EMAT[J].Transactions of China Electrotechnical Society, 2017,32(18):98-105.
[14] 刘素贞, 武云海, 张闯, 等. 静态偏置磁场强度对铁磁材料电磁超声换能机制的影响[J]. 电工技术学报, 2018, 33(9): 2148-2154.Liu Suzhen, Wu Yunhai, Zhang Chuang, et al. Effect of static bias magnetic field on electromagnetic ultrasonic transducer mechanism in ferromagnetic materials[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2148-2154.
[15] Ribichini R, Cegla F, Nagy P B, et al. Evaluation of electromagnetic acoustic transducer performance on steel material[J]. NDT & E International, 2011, 45(1):32-38.
[16] Han S W, Cho S H, Jang G W, et al. Non-contact inspection of rail surface and internal defects based on electromagnetic ultrasonic transducers[J]. Journal of Intelligent Material Systems & Structures, 2016, 27(3):427-434.
[17] Meitzler T J, Smith G, Charbeneau M, et al. Crack detection in armor plates using ultrasonic techniques[J]. Materials Evaluation, 2008, 66(6):2311-2369.
[18] Gavrić L. Computation of propagative waves in free rail using a finite element technique[J]. Journal of Sound & Vibration, 1995, 185(3): 531-543.
[19] 朱翔, 李天匀, 赵耀. 含环向表面裂纹圆柱壳的波传播特性研究[J]. 力学学报, 2007, 39(1): 119-124.Zhu Xiang, Li Tianyun, Zhao Yao. Wave propagation characteristics of cylindrical shells with circumferential surface crack[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(1): 119-124.
[20] Kim B, Roh Y. Simple expressions of the reflection and transmission coefficients of fundamental Lamb waves by a rectangular notch[J]. Ultraonics, 2011,51(6): 734-744.
[21] 刘素贞, 张严伟, 张闯, 等. 电磁超声管道周向兰姆波仿真分析及缺陷检测特性研究[J]. 电工技术学报, 2017, 32(22): 144-151.Liu Suzhen, Zhang Yanwei, Zhang Chuang, et al.Research on simulation analysis of electromagnetic ultrasonic circumferential Lamb waves and defect feature detection in pipeline[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 144-151.
[22] Ashigwuike E C, Ushie O J, Mackay R, et al. A study of the transduction mechanisms of electromagnetic acoustic transducers (EMATs) on pipe steel materials[J]. Sensors & Actuators A Physical, 2015,229: 154-165.