0 引言
六氟化硫（SF6）是高压电气设备中最常用的绝缘气体与灭弧介质。我国SF6年产量约7 000t，其中80%以上用于高压开关、断路器、输电管道等[1]。鉴于其超长大气寿命以及强烈吸收红外辐射的能力，SF6是迄今已知的全球变暖潜值（GWP=22 800）最高的温室气体，即每千克的 SF6产生的温室效应相当于排放22.8t CO2。随着我国SF6产业的迅猛发展，其所引发的温室效应已经增加到全球的1/3。面对日益严峻的环保压力，寻找能够替代SF6的新型绝缘气体已经成为化学与电气交叉领域的研究热点[2-6]。
然而环境友好型绝缘替代气体的研究非常具有挑战性。经过数十年的试验研究，依靠传统“试错”方法筛选出若干具备实用价值的替代气体，包括全氟酮（C5F10O, C6F12O）、全氟异丁腈（C4F7N）、八氟环丁烷（c-C4F8）、三氟碘甲烷（CF3I）等，如图1所示[7-11]。
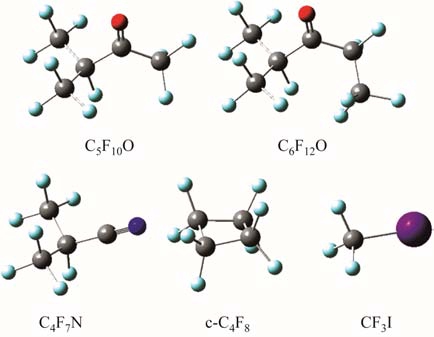
图1 若干SF6绝缘替代气体的分子结构
Fig.1 Molecular structures of the typical replacement gas for SF6
图中此类含氟化合物的绝缘强度比 SF6高，全球变暖潜能值（Global Warming Potential, GWP）远低于SF6，但是液化温度（沸点）远高于SF6，在低温环境中无法单独应用，一般需混合低沸点、低GWP的缓冲气体（例如 N2、CO2）。混合替代气体的优点是可能存在所谓的“协同效应”[12]，特别是气体混合后的表观绝缘性能甚至显著优于混合前的单质气体，即正协同效应；缺点是缓冲气体的绝缘强度较弱，混合并不总能产生正协同效应，且受气体类型、混合比例的影响较大。另外，目前所研制的替代气体多为含碳化合物，在金属电极或绝缘子表面放电后容易产生积炭，从而降低气体绝缘性能；同时混合气体通常不具备自恢复能力，灭弧性能普遍较差，无法用于更高电压等级的电气设备。
基于电气设备对绝缘性能的实际需求，理想的SF6替代气体需同时满足至少三项指标:绝缘强度高、液化温度低、GWP低。然而实践表明，这些指标之间常常相互制约、甚至相互矛盾。例如:绝缘强度高的气体，分子尺寸大、电负性强、电子吸附截面大，且对加热、光照、放电等均呈现化学惰性；但是，电负性强、体积大的分子之间存在较强相互作用，导致液化温度升高；分子越稳定则意味着在大气中越难以降解，大气寿命越长，导致 GWP增加。显然，满足单一指标的气体分子众多，同时满足三条指标则非常困难，SF6是目前唯一能够综合平衡各种矛盾的最佳分子结构。美国西屋电气公司研发中心的 R. E. Wootton等开展了数年的筛选工作，考察了大量替代绝缘气体分子，最终得到“没有一种气体能够全面优于SF6”的结论[13]。
气体绝缘与击穿是非常复杂的宏观现象，实验测量的临界击穿场强或击穿电压受各种条件的影响，包括电场类型（均匀电场、非均匀电场、极不均匀电场）、压力、温度、电极材料等，即便同一种绝缘气体也可能对应多个绝缘强度。测量气体的绝缘强度有多种实验方法[14]，包括气体击穿特性实验、稳态汤森实验、局部放电实验等，实验设备昂贵、数据分析复杂，工作量巨大。原则上，气体的绝缘强度亦可采用 Boltzmann方程或 Monte-Carlo模拟等数学物理方法计算，但需要电子与气体分子的各种碰撞截面作为输入参数，包括弹性碰撞截面、非弹性碰撞截面、电离截面、吸附截面、电子能量分布函数等[15]。鉴于电子与分子相互作用的复杂性，迄今只有少量简单气体分子碰撞截面的完整数据，显然无法满足快速筛选新型绝缘气体分子的需求。
在工业实践中，电气绝缘设备通常需要在高寒环境中使用。为了保证在低温条件下气体仍能够保持正常绝缘能力，液化温度是筛选替代气体的重要指标之一。液化温度是气体压力的函数，标准大气压下的液化温度即为气体的正常沸点（Tb）。为满足工业需求，不仅需要绝缘气体的沸点尽可能低，而且要求在高压条件下（例如输电管道压力可达5~10个大气压）不能液化。气体液化温度与 GWP的实验测量亦相当繁琐，前者需测量不同温度下的饱和蒸气压，后者需测量大气寿命和吸收光谱等[16]。与此同时，绝缘强度、液化温度、GWP实验测量均需要消耗大量的气体样品，甚至需自行合成，实验研究成本极高。
综上所述，突破绝缘气体性能指标之间的固有矛盾，揭示绝缘、液化、环保特性的物理化学本质，掌握绝缘气体分子的构建原理与绝缘规律，是解决SF6替代气体瓶颈难题的唯一途径。通过关联宏观特性指标与气体分子的某些微观物理化学参数，建立构效关系模型，预测或评价任意气体的绝缘强度、液化温度、GWP，优化搜索能够同时满足“绝缘强度高、液化温度低、GWP低”三个指标要求的分子结构，是发现综合性能最优替代气体的有效手段。
气体分子结构与绝缘性质的关联规律早已受到广泛关注。为了促进SF6绝缘替代气体的实验研究，本文对环保绝缘气体的构效关系与分子设计研究进行了综述，着重分析了国内外相关研究工作的最新成果，总结了各种构效关系模型与分子设计的优势及适用性，进而提出行之有效的 SF6替代气体分子设计技术，以推动新型环保绝缘气体在电气行业的快速发展与应用。
1 早期定性模型
早在1942年，B. M. Hochberg和E. Y. Sandberg通过试验研究发现一些气体的绝缘强度与分子折射率有关[17]。1950年，W. A. Wilson等发现含氟烃气体的绝缘强度与分子量（Mw）或标准状态下的质量密度（ρ= pMw/(RT), p为压强，T为热力学温度，R为常数）存在相关性[18]。1956年A. E. D. Heylen和T. J. Lewis提出烷烃气体分子的绝缘强度与其紫外光谱、Ramsauer截面有关[19]。1959年P. Narbut等通过观察一些气体的绝缘特性，亦发现气体绝缘强度与相对分子质量有关[20]:相对分子质量越大，电离截面越低、电子附着截面越高，从而具有较高的绝缘强度。这一定性规律受到 J. H. Mason, C. M.Cooke, A. H. Cookson等的支持[21-22]，他们发现大量气体的绝缘强度与相对分子质量之间的确存在某种线性规律。例如，虽然 SF6分子与 He原子完全不同，但二者在相同质量密度下的绝缘强度相同。
1976年A. K. Vijh提出某些气体的绝缘强度与原子化焓相关[23]，但不适用于更宽范围的气体类型。紧接着他又提出气体的绝缘强度与沸点存在近似正比关系，当然仍存在众多例外[24]。1982年A. K. Vijh系统考察了82种气体分子的绝缘特性，发现替代气体相对于SF6绝缘强度Er与质量密度ρ呈现A、B两种不同的线性关系[25]，如图2所示。虽然该模型能在某种程度上显示气体绝缘强度随质量密度线性变化的某种趋势，但是无法解析产生两种线性关系的原因，且存在许多例外。例如He的质量密度（ρ=0.18g/L）是H2（ρ=0.09g/L）的 2倍，但是He的绝缘强度仅为H2的30%，显然，以上定性模型只能用作一级近似，辅助判断气体的绝缘性质。
2 定量构效关系模型
1974年J. C. Paul等提出了首个计算常压下气体相对绝缘强度的定量关系式[26]，即
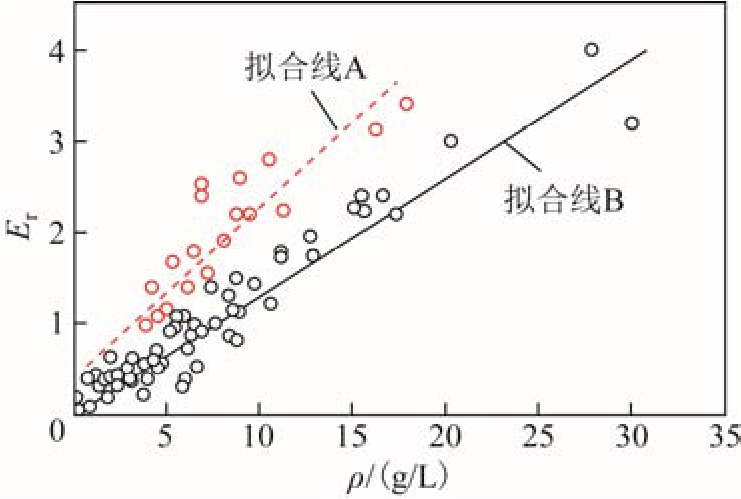
图2 绝缘强度随相对分子质量密度变化关系
Fig.2 Dependence of dielectric strengths on the molecular mass densities
式中，α、ε i、εD分别为气体分子的极化率、电离能、键解离能。此公式只能用于某些特定气体，无法正确描述大多数电负性气体的绝缘特性。
1979年K. P. Brand与J. Kopainsky重新考虑了气体的击穿行为[27]，基于常用的近似击穿判据（电离系数α=附着系数η），获得了定量计算绝缘强度的改进表达式，即
式中，ζb为电子每次碰撞平均损失的能量；σ为动量传递截面；e、me分别为电子的电量与质量；εDA为电子发生解离性附着的阈能。此公式避免了使用键解离能参数，更符合气体击穿的物理本质，但是其中的输入参数无法直接获得，难以应用于分子设计实践工作。
1982年K. P. Brand系统研究了41种气体的绝缘强度与液化温度随分子参数的变化规律[28]，建立了首个真正意义上的预测气体绝缘强度的构效关系模型。针对不同气体分子的结构差异性以及实验测量数据的分散性，提出了筛选训练数据集的三条严格标准:①均匀电场；②统一气体压力p与放电间距d（即单一pd值），根据Paschen定律，尽可能地选择较大的pd值，例如选择p＞1 kPa⋅m，从而有效避免近距离放电的复杂性；③多组实验数据能够交叉验证。基于41种气体分子的最小二乘线性拟合分析，K. P. Brand给出了绝缘强度的表达式为
式中，电离能εi和极化率α的单位分别为 eV和10-30m3，拟合效果如图3所示。
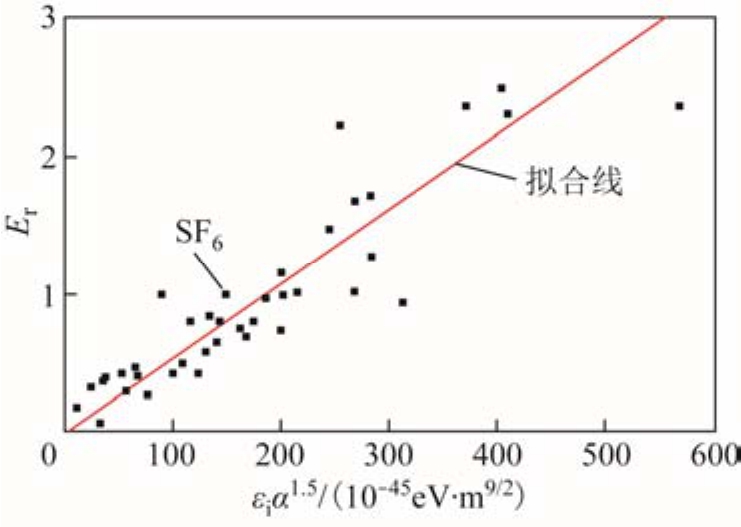
图3 绝缘强度随电离能和极化率的变化关系
Fig.3 Relationship of dielectric strengths with ionization potentials and polarizability
图3 所示理论模型的相关系数R=0.91，说明气体的绝缘强度应该与气体分子的电离能、极化率存在较为密切的依赖关系。另一方面，从图3很明显可以看出，模型预测的绝缘强度与实测值仍比较发散，例如c-C6F12的绝缘强度为2.35，预测值却高达3.08，理论与实验偏差达到了 31%；然而，对于和c-C6F12具有相同绝缘强度的CCl4气体，理论预测值为2.01，偏低约15%。更重要的是，该模型预测SF6的绝缘强度仅为 0.8，不能正确计算 SF6的绝缘强度，将大大限制该模型的预测能力与适用范围。
2004年 N. Meurice首次采用量子化学计算方法，优化分子结构与光谱参数，建立了气体绝缘强度的构效关系模型[29]。他们从电子失能谱角度入手，考虑到放电过程中电子穿越气体介质的介电物理图像，定义近似电子失能函数L(ω)为
式中，ω为光激发频率；ε2(ω)为气体介电函数的虚部。采用密度泛函理论（Density Functional Theory,DFT）方法，在BLYP/DNP理论水平上计算了43种气体分子结构与积分光吸收强度IOA参数，发现绝缘强度与（IOA）存在如下正比关系，即
遗憾的是，该模型的相关系数R仅为0.85，预测SF6的绝缘强度仅为0.8，且较为发散，甚至无法正确描述简单的N2气体，其绝缘强度理论预测值比实验值偏低了将近40%之多。同时，采用量子化学方法获得IOA数据较为困难，计算量大、效率低且误差较大。
2007年A. Olivet等基于同样43种气体分子，换用计算量小、效率更高的半经验量子化学方法（PM3、AM1），研究了气体绝缘强度与电离能、电子亲合能的关系[30]。发现气体的绝缘强度与电离能并不存在定量关联，与电子亲合能的线性相关也很差，相关系数仅为0.61，因此，仅仅依赖简单的电子结构参数预测气体绝缘强度前景不容乐观。
2013年M. Rabie等采用DFT方法，在BP86/def-TZVP和BP86/def2-QZVPP理论水平上计算了67种气体分子的各种电子结构描述符[31]，包括极化率α、偶极矩μ、垂直电离能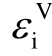
、绝热电离能
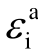、垂直电子亲合能
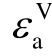、绝热电子亲合能
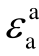、能隙ΔEgap，并联合分子量Mw、电子数Ne作为描述符，对67种气体的绝缘强度数据进行多元线性回归分析，即
式中，p0、p1、p2为待定参数；x1、x2为描述符参数。试图建立计算气体绝缘强度的构效关系模型。
研究发现无论分子量、电子数等简单参数，还是极化率、电离能等参数，均无法获得可靠的理论模型。例如，对于使用电子数Ne为描述符的线性函数，其相关系数仅为0.71，且数据发散。因此，M.Rabie等将67种气体分成极性与非极性分子两类分别考虑，并通过复杂统计回归分析，建立了两种最优构效关系模型，即
（1）48种极性分子（相关系数R=0.84）
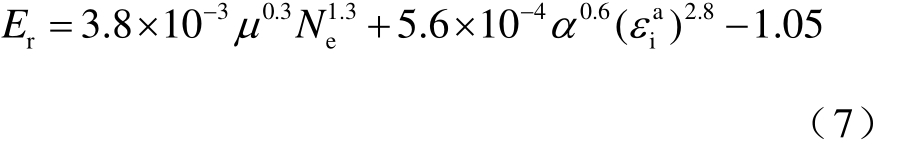
（2）19种非极性分子（相关系数R=0.96）
绝缘强度的计算值与实测值的对比如图4所示。
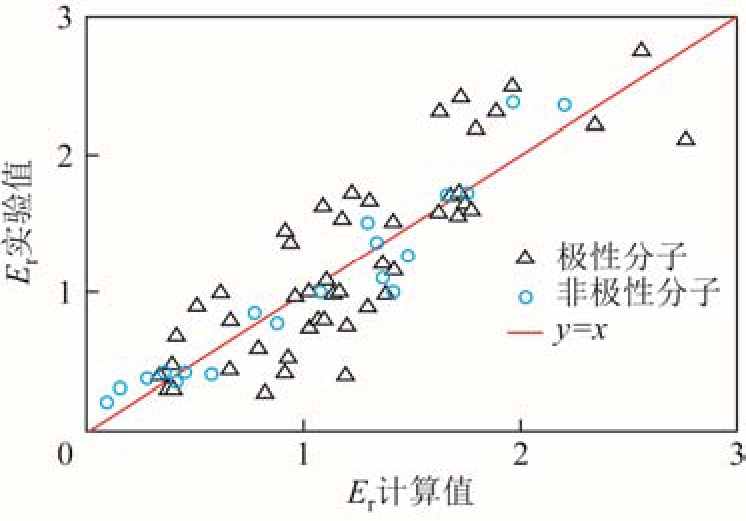
图4 绝缘强度计算值与实验值的比较
Fig.4 Comparison of the experimental dielectric strengths to the calculated data
与更早的构效关系模型相比，该两种模型的可靠性与预测能力均有明显提高，理论计算相对较为简便，但是存在两方面的缺陷:一是相关函数表达式较为复杂，参数组合方式显然缺乏明确的物理意义；二是对于实验数据更多的极性分子而言，其相关系数反而比非极性分子更差，说明该构效关系模型不能反映气体绝缘强度随分子结构变化的规律，很可能仅是数值巧合。
2016年 C. Zhang等采用 DFT方法，在 M06-2X/6-311+G(3df)理论水平上计算了 24种气体分子的极化率与电子亲合能，并获得了相应的线性回归表达式[32]，即
虽然使用了更少的训练数据库（24种未知气体的绝缘强度在0~1.2范围），但此模型的相关系数仅为0.78，可靠性明显低于Rabie模型。
3 新型构效关系模型
绝缘强度是气体抵抗外电场能力的宏观表现，反映了电子与分子之间的相互作用。同时，绝缘现象是大量气体分子受外电场作用的统计行为，绝缘强度不仅与气体分子本性有关，而且与分子间相互作用存在必然联系。虽然前人发展了若干定性或定量模型预测气体的绝缘强度，但仍局限于简单物性参数的描述，缺少能够直接反映电子-分子、分子-分子之间相互作用的物理量，无法获得可靠的构效关系模型。另一方面，构效关系模型强烈依赖于训练集数据库。虽然已经积累了大量气体绝缘强度的实验数据，但是由于测量技术手段与实验条件的差异，导致实验数据较为分散。因此，缺少可靠的气体绝缘强度实验数据库，也是阻碍构效关系模型发展的重要因素。经过系统深入探索，本文建立了能够准确预测任意气体绝缘强度的新型构效关系模型，并用于SF6替代分子设计研究。
3.1 绝缘强度实验数据库
首先建立了可靠的气体绝缘强度实验数据库，包含43种气体分子，见表1。除了参考K. P. Brand的三条筛选标准之外，为保证绝缘强度数据的有效性，本文增加了两条筛选标准:①在实验测量过程中以 SF6为内标，这是因为只有通过测量气体的击穿电压与相同条件下 SF6的击穿电压比值，才能获得构效关系模型所依赖的可靠绝缘强度；②针对不同实验测量结果，差别明显的气体分子，其绝缘强度显然存在争议，因此从数据库中剔除。例如 SO2气体，其绝缘强度的实测数据分散在0.52~1.5的范围内，即实验上甚至未能明确SO2与SF6气体绝缘能力的相对强弱问题[13]，显然不能用于建立构效关系模型。从表1可以看出，绝缘强度实验数据库包含由 2~18个 C、H、O、N、S、F、Cl、Br等原子组成的各类有机或无机气体分子，例如烷、烯、炔、醚、酮、酯、腈、环氧、硫酰等化合物，气体种类较齐全，绝缘强度在0~3之间，分布范围较广，适合用于构效关系模型研究[33]。
表1 筛选后的绝缘强度数据库
Tab.1 Database for the experimental dielectric strengths
分子 CAS注册号 Er 分子 CAS注册号 Er H2 1333-74-0 0.22 CF3CF2Cl 76-15-3 1.04 O2 7782-44-7 0.33 F2C=CFCl 79-38-9 0.72 N2 7727-37-9 0.38 CF3CH=CH2 677-21-4 0.80 N2O 10024-97-2 0.46 CF3CF=CF2 116-15-4 0.94 CO 630-08-0 0.40 CF2=CF-CF=CF2 685-63-2 1.20 CO2 124-38-9 0.35 c-C6F10 355-75-9 1.90 OCS 463-58-1 0.90 c-C4F8 115-25-3 1.25 SF6 2551-62-4 1.00 c-C6F12 355-68-0 2.35 CH4 74-82-8 0.43 c-CF3(C4F6)CF3 1583-97-7 2.30 CH3Cl 74-87-3 0.32 CF3OCF3 1479-49-8 1.00 CH3Br 74-83-9 0.45 c-CF3(C2F2O)CF3 117642-58-7 1.60 CH2F2 75-10-5 0.27 HC≡CH 74-86-2 0.60 CH2Cl2 75-09-2 0.68 SO2F2 2699-79-8 0.73 CHF2Cl 75-45-6 0.42 CF3SO2F 335-05-7 1.45 CHFCl2 75-43-4 0.92 CH3CN 75-05-8 0.80 CF4 75-73-0 0.42 CF3CN 353-85-5 1.50 CF3Cl 75-72-9 0.58 C2F5CN 422-04-8 2.00 CF2Cl2 75-71-8 0.99 C3F7CN 375-00-8 2.40 CF3Br 75-63-8 0.75 i-C3F7CN 42532-60-5 2.20 CH3CF3 420-46-2 0.41 i-C3F7COCF3 756-12-7 2.10 CH3CHCl2 75-34-3 1.01 i-C3F7COC2F5 756-13-8 2.80 C2F6 76-16-4 0.80
3.2 相互作用性质函数
为了正确描述电子-分子、分子-分子间相互作用，本文选取电子密度与静电势作为描述气体绝缘特性的基本物理量，并采用相互作用性质函数（General Interaction Properties Function, GIPF）方法[34]，构造各种反映分子结构、形貌以及静电相互作用的描述符，通过统计回归分析，建立构效关系模型。
取电子密度为0.001(au)的等值面构建分子表面，计算分子表面上每一点r处的静电势，即
式中，ZA为核电荷；RA为原子核坐标；ρ(r')为电子密度。据此分析各种具有物理意义的静电势统计量，包括:分子正、负静电势的分表面积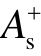 
、
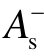和总表面积 As；正、负静电势的平均值
和总平均值
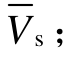表面静电势的正、负方差 
和总方差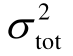
；正、负静电势的平衡度
静电势平均偏差Π，表示分子表面电荷分离程度或局域极性。采用多元非线性回归方法，设置绝缘强度计算值与实验值的相关系数与均方差收敛标准，优化搜索与绝缘强度的相关函数，获得最佳构效关系模型，即
式中，各项符号含义如前所述。
除了电子密度与静电势，本文还引入了电负性χ与硬度η两个参数，分别用于描述电子与分子的相互作用以及分子在外场作用下的形变:χ=(I+A)/2,η=(I-A)/2，式中电离能 I、电子亲合能 A与分子的最高占有轨道（Highest Occupied Molecular Orbital,HOMO）、最低空轨道（Lowest Unoccupied Molecular Orbital, LUMO）有关。
众所周知，相关系数R是衡量构效关系模型优劣的重要指标，但是相关系数仅表示理论与实验数据的相关程度，并不能直接反映计算值与实验值的吻合程度。因此，除了相关系数，本文将理论与实验值的平均绝对偏差（Mean Absolute Deviation,MAD）、方均根误差σ以及最大偏差δ max用于检验构效关系模型的可靠性。与此同时，鉴于表1中的实验数据均以 SF6为内标，能否准确计算 SF6的介电强度（ 6r,SF 1E = ）也是检验构效关系模型可靠性的关键指标。
GIPF已经被成功用于研究物质的各种宏观特性，包括沸点、凝固点、表面张力、密度、扩散等[34]。值得指出的是，GIPF中的参数均可以通过量子化学计算直接获得。更重要的是，虽然分子的静电势受计算方法影响较大，但对构效关系模型的影响较小。通过对比HF、MP2、B3LYP、M06-2X等不同理论方法的结果表明，虽然 GIPF参数绝对数值存在差异，但是均可以给出较好的相关函数。
3.3 构效关系模型
3.3.1 模型I
本文考察了11种GIPF参数，最终发现只有As、νσ tot2、Π 三组参数与绝缘强度存在显著相关，优化后得到构效关系模型Ⅰ为
相关系数 R=0.991、MAD=0.065、σ =0.090、δmax=0.32均表现较好，但SF6的理论绝缘强度仅为0.88，偏离实验值较大。需要指出的是，建立构效关系模型的意义不仅在于准确预测未知气体的绝缘强度，而且可以揭示绝缘强度受分子结构影响的规律，据此可以获得提高绝缘强度的指导性方案，比如:增加分子总表面积、增强分子表面上正、负静电势的平衡、降低局域极性，从而开展合理化分子设计，为新型替代气体的研发提供理论依据。从模型I可以看出，绝缘强度对分子的局域极性（Π）非常敏感。SF6的Π = 0.09，其局域极性（即分子内电荷分离程度）最低；而同为非极性分子的 CF4，Π 值约为 SF6的 2倍，显然局域极性导致 CF4的绝缘强度远低于SF6。
3.3.2 模型Ⅱ
引入分子极化率α与电负性χ参数后，优化得到构效关系模型II为
该模型的各项评价指标为 R=0.992、MAD=0.061、σ =0.083、δmax=0.34、 E r, SF6 = 0 .96，可以看出模型Ⅰ中 SF6绝缘强度偏低的缺点得到明显改善。与模型Ⅰ相比，模型Ⅱ中As的贡献约降低30%，表明极化率与电负性对提高介电强度均有正效应。
如前所述，分子的电负性参数取决于电离能（IP）和电子亲合能（EA），然而这两个参数（特别是EA）是量子化学计算的难点[35]。严格地讲，EA包括垂直吸附（VAE）、解吸（VDE）亲合能与绝热亲合能（EA）三种定义。采用绝缘气体分子的垂直电离能与垂直吸附亲合能重新计算电负性参数，改进的构效关系模型为
可以看出，As、νσtot2、Π的参数变化很小，αχ的贡献降低了约14%，评价指标（R=0.992、MAD=0.062、
亦基本保持不变，说明仅通过改变电负性参数无法获得更好的相关模型。
事实上，常用的量子化学方法比如DFT并不适合用于计算阴离子体系[36]，所得的 HOMO能量通常为正值，即阴离子不是成键态。虽然文献中已经发展了许多改进的量子化学计算方法，但仍存在各种缺陷[37-38]，即使对于 SF6分子的 EA计算迄今仍存在广泛争议[39-41]。另一方面，并不是所有分子都存在稳定的正、负离子结构，某些分子失去或捕获电子后随即解离。虽然在电气工程领域传统认为气体的绝缘能力与电负性有关，而且绝缘气体往往被称为“电负性气体”，但实际上气体的绝缘强度与电离能、电子亲合能并不存在显著相关性[42]。
模型Ⅱ的另外一个缺陷在于存在过度参数化问题。研究发现分子表面积As与极化率α 两个关键参数存在显著依赖关系，如图5所示，即
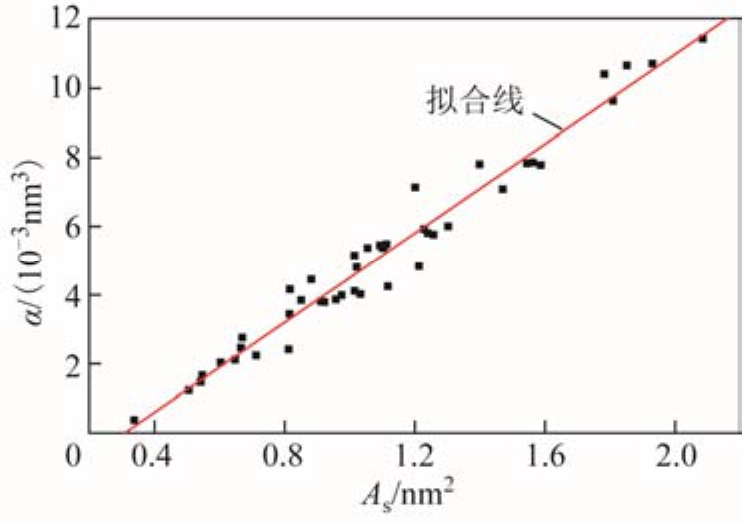
图5 分子极化率与表面积的关系
Fig.5 Molecular polarizability and surface area
因此，在模型Ⅱ中 As与α并不是合理的独立变量，为避免过度参数化只能保留其一。将极化率对介电强度的贡献隐含在表面积中，得到改进模型Ⅱ为
与同为三个参数的模型Ⅰ相比，改进模型Ⅱ的相关系数R=0.991保持不变，σ =0.089、δmax=0.30、SF6的介电强度（ E r, SF6 = 0 .91）均有所改善，但是MAD=0.069明显变差，说明在该构效关系模型中缺失了绝缘强度所依赖的关键因素。若要进一步提高构效关系模型的精度，则必须引入新的电子结构参数。
3.3.3 模型Ⅲ
在电子-分子碰撞过程中，实际上只有正静电势
所贡献的表面积 
与绝缘强度直接相关。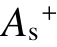
表示分子中能够用来吸附电子的表面区域，
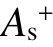越大，分子吸附电子的能力越强。虽然负静电势的表面积
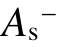与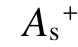
在数值上相当，但是 
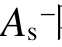随绝缘强度的变化没有规律，总表面积As与、
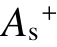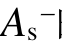的相关性也不明显。
除了表面积，分子形貌也是影响电子与分子相互作用的潜在因素，但分子表面积并不能直接反映分子形状的信息。因此，本文定义约化表面积
参数，即
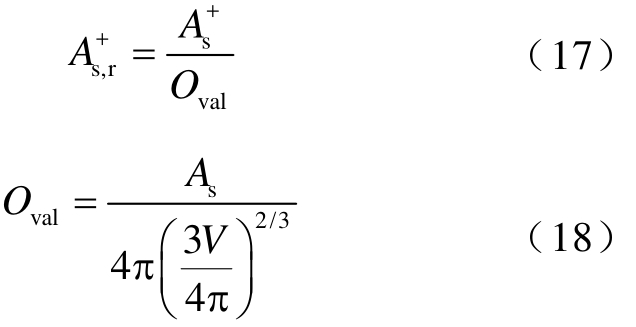
式中，V为分子体积；Oval为分子椭圆度，Oval反映了分子形貌（即电子密度为0.001(au)的等值面）偏离完美球体的程度。计算表明，绝缘强度与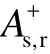 
存在显著相关，相关系数达到0.967。
如前所述，40年前A. K. Vijh发现气体的绝缘强度的确存在随分子量或标准状态下的质量密度增加而升高的趋势[25]。在电子与分子碰撞过程中，与小分子相比，质量高、密度大的分子显然能够更加有效地通过非弹性碰撞传能大幅度降低自由电子的动能，从而表现出更强的绝缘能力。受此启发，本文定义分子密度作为关联绝缘强度的参数，即
需要指出的是，分子密度ρ与气体的实际密度（随温度、压力变化）不同，它表示分子处于紧密堆积状态时的理想密度，是一个与分子所处的相态无关的物理量，近似对应于绝对零度下完美分子晶体的密度。
在 M06-2X/6-31++G(d,p)理论水平上计算得到43种绝缘气体分子的 As
参数，回归得到最优化构效关系模型III[43]为
绝缘强度的理论值与实验值的比较如图6所示。模型Ⅲ的相关系数 R = 0.993、MAD=0.061、σ =0.080、δmax=0.28，同时SF6的绝缘强度为0.99，各项指标明显优于其他模型。该模型中所有参数均为独立变量，各变量之间没有相关性。
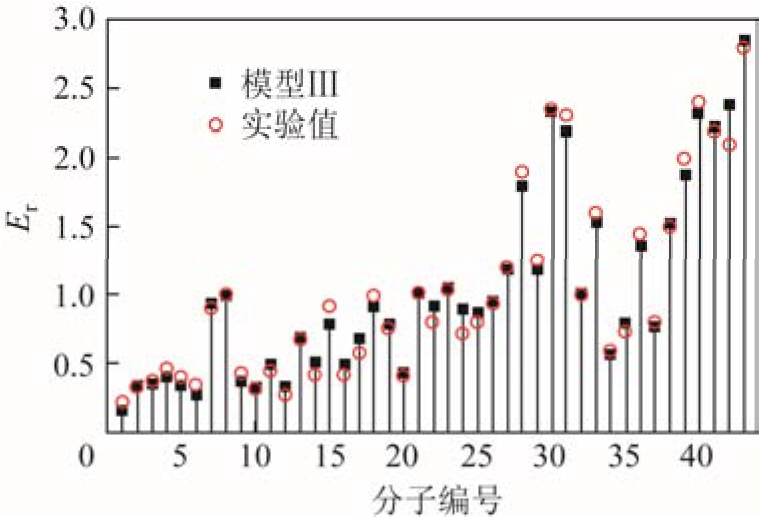
图6 绝缘强度的计算值与实验值的比较
Fig.6 Comparison of the predicted dielectric strengths by model Ⅲ with the experimental data
模型Ⅲ除了能够准确预测任意气体的绝缘强度之外，还揭示了绝缘强度受分子结构影响的规律。总之，气体的绝缘强度主要取决于四方面:①与分子总表面积描述符As有关的性质；②与分子正、负静电势的分离程度描述符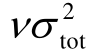
有关的性质；③与分子的局域极性描述符Π有关的性质；④与电子吸附截面有关的
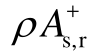r 描述符。其中
均为正贡献，而Π 为负贡献。As对绝缘强度的影响最为显著，对于高绝缘强度的气体分子，As的贡献可达75%以上。虽然增加As与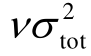
均有利于提高绝缘强度，但是As与
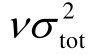是一对相互矛盾的物理量:As的贡献越大，则
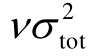的贡献越小；当As的贡献占比为50%以下时，随着As增加，
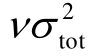的贡献则由40%下降至10%左右；当As的占比超过50%时，
的贡献则迅速减小到1%以下。对于绝缘能力比SF6弱的气体分子，Π 贡献率约为30%左右，表明强局域极性是导致气体绝缘能力变弱的重要原因。对于绝缘强度高于SF6的气体分子，Π 贡献率降为10%左右，局域极性的影响变弱。虽然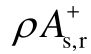
对介电强度的影响普遍较小，但是它可以有效补偿Π 对介电强度的负贡献，对于提高分子的绝缘强度非常有利，该参数为设计新型绝缘气体分子提供了新方向。
腈化物分子的绝缘强度如图7所示，模型Ⅲ不仅正确预测了新型绝缘气体全氟异丁腈（C4F7N）的绝缘强度，与实验值一致，而且正确给出了氰化物的绝缘强度随链长、氟取代基的变化规律。
图7 腈化物分子的绝缘强度
Fig.7 Dielectric strengths of the nitriles
模型Ⅲ的成功源于它同时考虑了分子尺寸、分子拓扑形貌、电子-分子间作用、分子-分子间作用等与绝缘直接相关的参数，与以往构效关系模型中所采用的偶极矩、极化率、电离能、电负性等经验参数不同，模型Ⅲ的参数均为绝缘物理及化学本质的反映，具有明确的定义和物理意义，且不依赖任何人为因素，能够采用量子化学方法直接计算获得。因此，模型Ⅲ非常适合用于大规模 SF6替代气体筛选与分子设计研究工作。
4 SF6替代气体分子设计
与构效关系模型相比，分子设计是一项更具挑战性的工作。如前所述，对于 SF6替代气体分子而言，只有在多种相互矛盾的性质（比如绝缘强度与液化温度）之间寻找平衡点，才能设计出具备实际应用价值的气体分子。依靠试验寻找平衡点的工作量大、效率低，借助构效关系模型则可以迅速判断合理的分子设计方向[45-49]。
4.1 官能团取代设计
官能团取代是最常用的设计新型化合物的手段，例如3M公司最新推出的C4F7N分子（Novec 4710），可以通过氰基（CN）取代八氟丙烷的一个氟原子直接得到，如图8所示。
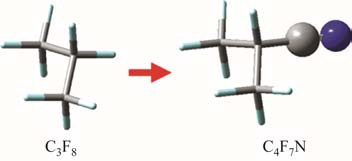
图8 氰基取代C3F8形成C4F7N
Fig.8 Formation of C4F7N by the CN-substituted C3F8
针对 SF6替代气体分子，本文采用 CF3、NF2、Cl、CN基团依次取代SF6的1~6个F原子，获得了一系列新型气体分子，基于构效关系模型考察了绝缘强度与液化温度随分子结构的变化规律，部分结果如图 9所示[33]。很明显，CF3取代对提高绝缘强度最有效而对液化温度的影响最弱，是一种较为理想的分子设计方向，但是此类气体分子的 GWP仍然较高，例如SF5CF3的GWP=17 770，无法满足环保要求。因此，依据图9结果发现CN取代是一种更为理想的分子设计方案，计算预测单取代SF5CN分子的绝缘强度为 1.55，沸点为-30 oC（与实验值-26 oC吻合），GWP仅为SF6的5%左右，是一种潜在的SF6替代气体。
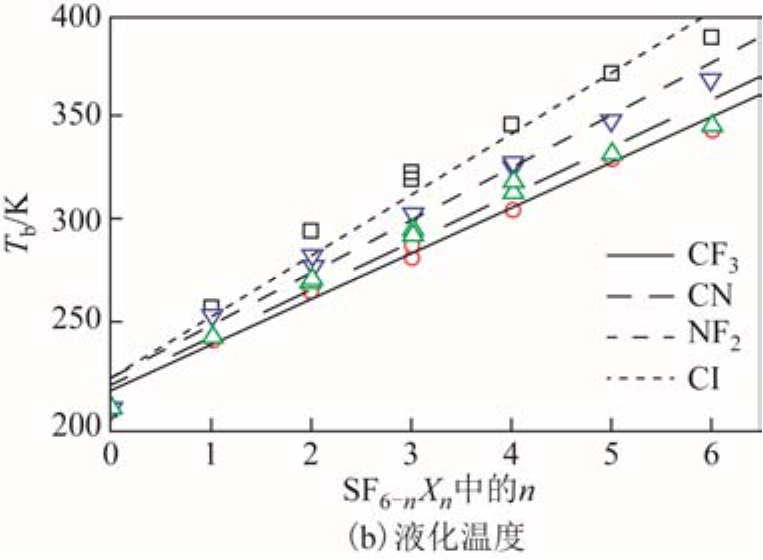
图9 CF3、NF2、CN、Cl官能团取代SF6形成分子的绝缘强度与液化温度
Fig.9 Dielectric strengths and boiling points of the substituted SF6 molecules
4.2 分子杂化设计
通过官能团取代方式虽然能够获得新气体分子，但难以获得包含新型化学键的全新分子结构。混合绝缘气体已经在电气领域得到广泛应用，包括常规的 SF6+N2混合气体、新型的 C4F7N+CO2混合气体（g3）、甚至三元混合气体C4F7N+CO2+CF4等。物理混合后的气体之所以能够满足应用指标主要得益于气体分子间的绝缘协同效应。受此启发，本文提出了一种“化学混合”分子设计思想，即将两种或两种以上分子通过“杂化”（hybrid）形成新型化学键[44]。图10展示了 SF6与 N2杂化后形成 F3S≡N分子的机理。与 50%SF6 + 50%N2形成的混合气体不同，50%SF6 + 50%N2杂化后的 F3S≡N分子通过 S≡N三重键连接，形成全新的分子结构。
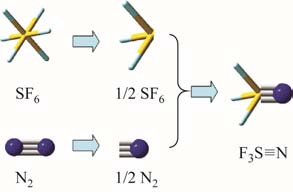
图10 SF6与N2分子通过化学杂化形成F3SN的机理
Fig.10 Mechanism for the formation of F3SN through hybrid SF6 and N2
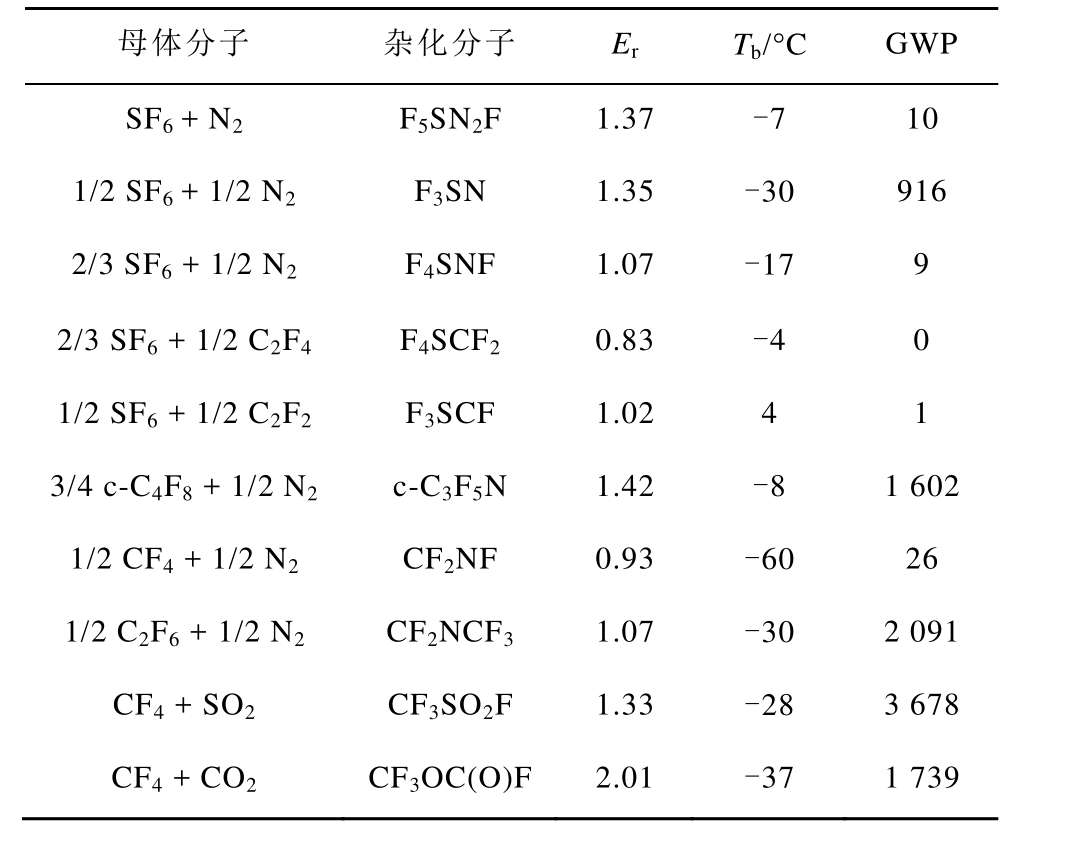
基于分子杂化思想，本文设计了一系列新型气体分子，并采用构效关系模型预测了绝缘强度、液化温度、GWP，见表 2，分子结构及分子表面静电势如图11所示。可以看出，杂化分子的绝缘强度超过 SF6或者相当，液化温度较低，且均为环境友好型替代气体。
表2 杂化分子的绝缘强度、液化温度、GWP
Tab.2 Dielectric strengths, boiling points, and GWP of the hybrid molecules
母体分子 杂化分子 Er Tb/°C GWP SF6 + N2 F5SN2F 1.37 -7 10 1/2 SF6 + 1/2 N2 F3SN 1.35 -30 916 2/3 SF6 + 1/2 N2 F4SNF 1.07 -17 9 2/3 SF6 + 1/2 C2F4 F4SCF2 0.83 -4 0 1/2 SF6 + 1/2 C2F2 F3SCF 1.02 4 1 3/4 c-C4F8 + 1/2 N2 c-C3F5N 1.42 -8 1 602 1/2 CF4 + 1/2 N2 CF2NF 0.93 -60 26 1/2 C2F6 + 1/2 N2 CF2NCF3 1.07 -30 2 091 CF4 + SO2 CF3SO2F 1.33 -28 3 678 CF4 + CO2 CF3OC(O)F 2.01 -37 1 739
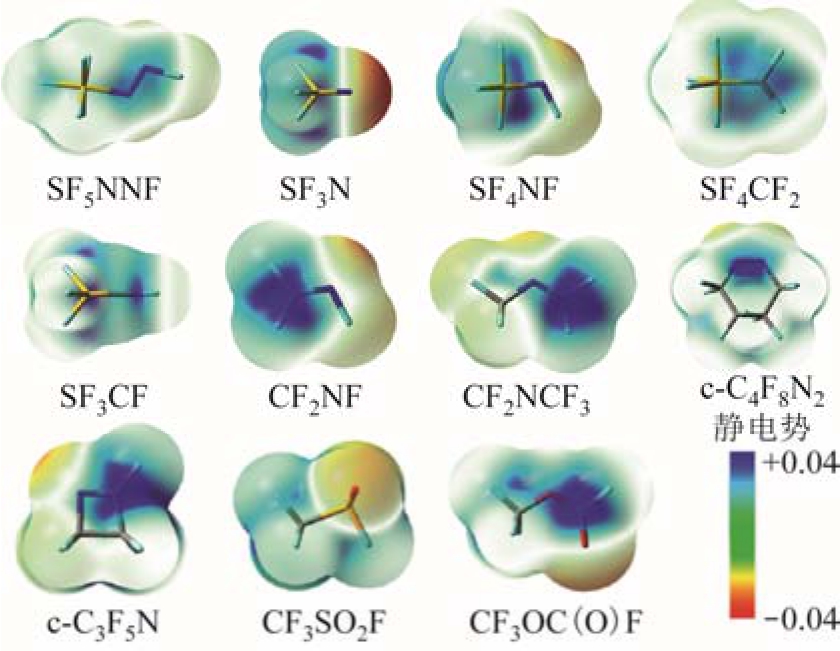
图11 若干杂化分子的结构与表面静电势
Fig.11 Structures and electrostatic surfaces of the typical hybrid molecules
对于部分气体分子，其理论预测的液化温度与实验值吻合，验证了分子设计的可靠性。杂化分子之所以具有较强的绝缘能力，可以从构效关系模型得到合理解释。表3列出了SF6、N2、F3SN分子的关键参数。与SF6相比，F3SN的表面积虽然略微减小，分子的局域极性较高（Π =0.38），但表面静电势的统计方差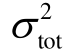
远高于 SF6，且具有与 N2相同的完美正、负静电势平衡度（ν =0.25），因此F3SN的绝缘强度比SF6提高了35%。综合液化温度与GWP数据，可以预测 F3SN应是一种能够替代 SF6的新型环保绝缘气体分子。
表3 F3SN与母体分子的GIPF参数比较
Tab.3 Comparison of the GIPF parameters of F3SN with those of the parent molecules
分子 As/nm2 ν 2σ /(kcal/mol)2 Π /eV tot SF6 1.03 0 7.92 0.09 N2 0.54 0.25 10.28 0.17 F3SN 0.94 0.25 80.30 0.38
与物理混合气体（比如常用的 SF6/N2）相比，杂化设计得到的单质气体不仅具有更好的绝缘性能，而且可以有效避免在电气设备中使用混合气体的潜在困难，诸如最优混合比的优化与保持、混合气体浓度控制、混气的配制和回收等难题。另外，本文设计的新型杂化分子结构简单，合成路线也不复杂。分别以常见的二氯化二硫（S2Cl2）、三氟甲基磺酰氯为（CF3SO2Cl）为原料，目前已经成功实现了 F3SN、CF3SO2F两种新型绝缘气体的实验室合成[50-51]。实验测量 CF3SO2F气体的绝缘强度为1.33，与理论计算结果完全一致，进一步验证了本文构效关系模型与分子设计的合理性与可靠性。
5 结论
1）基于分子量、折射率、电负性等参数的定性模型只能用作一级近似，辅助定性判断气体绝缘强度的变化趋势。
2）基于电离能、电子亲合能、极化率、吸收光谱等简单参数的理论模型，缺少明确的物理图像，计算复杂、适用范围窄、可靠性无法保证，难以用于大批量绝缘气体分子筛选。
3）基于分子尺寸、拓扑形貌、表面静电势统计性质函数的构效关系模型，物理意义明确、预测结果稳定可靠，计算简单，是一种切实可行的评价替代气体绝缘性能的新方法。
4）官能团取代设计与分子杂化设计均能发现绝缘强度、液化温度、GWP等综合性能与 SF6相当，甚至优于 SF6的新型气体分子，在 SF6替代气体研究领域具有较好的应用前景。
[1] Fang Xuekun, Hu Xia, Greet J M, et al. Sulfur hexafluoride (SF6) emission estimates for China: an inventory for 1990-2010 and a projection to 2020[J].Environmental Science & Technology, 2013, 47(6):3848-3855.
[2] Okubo H, Beroual A. Recent trend and future perspectives in electrical insulation techniques in relation to sulfur hexafluoride (SF6) substitutes for high voltage electric power equipment[J]. IEEE Electrical Insulation Magazine, 2011, 27(2): 34-42.
[3] Franck C M, Dahl D A, Rabie M, et al. An efficient procedure to identify and quantify new molecules for insulating gas mixtures[J]. Contributions to Plasma Physics, 2014, 54(1): 3-13.
[4] Kieffel Y, Irwin T, Ponchon P, et al. green gas to replace SF6 in electrical grids[J]. IEEE Power and Energy Magazine, 2016, 14(2): 32-39.
[5] Beroual A, Haddad A. Recent advances in the quest for a new insulation gas with a low impact on the environment to replace sulfur hexafluoride (SF6) gas in high-voltage power network applications[J].Energies, 2017, 10(8): 1216(1-20).
[6] 周文俊, 郑宇, 杨帅, 等. 替代 SF6的环保型绝缘气体研究进展与趋势 [J]. 高压电器, 2016, 52(12): 8-14.Zhou Wenjun, Zheng Yu, Yang Shuai, et al. Research progress and trend of SF6 alternative with environment friendly insulation gas[J]. High Voltage Apparatus,2016, 52(12): 8-14.
[7] Stoller P C, Doiron C B, Tehlar D, et al. Mixtures of CO2 and C5F10O perfluoroketone for high voltage applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(5): 2712-2721.
[8] Mantilla J D, Gariboldi N, Grob S, et al. Investigation of the insulation performance of a new gas mixture with extremely low GWP[C]//IEEE Electrical Insulation Conference, Philadelphia, PA, USA, 2014: 469-473.
[9] Nechmi H E, Beroual A, Girodet A, et al.Fluoronitriles/CO2 gas mixture as promising substitute to SF6 for insulation in high voltage applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(5): 2587-2593.
[10] Yamamoto O, Takuma T, Hamada S, et al. Applying a gas mixture containing c-C4F8 as an insulation medium[J]. IEEE Transactions on Dielectrics &Electrical Insulation, 2001, 8(6): 1075-1081.
[11] Katagiri H, Kasuya H, Mizoguchi H, et al.Investigation of the performance of CF3I gas as a possible substitute for SF6[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2008, 15(5): 1424-1429.
[12] Osmokrovic P, Stojkanovic M, Stankovic K, et al.Synergistic effect of SF6 and N2 gas mixtures on the dynamics of electrical breakdown[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(2):677-688.
[13] Wooton R E, Kegelman, M R. Gases superior to SF6 for insulation and interruption[R]. Electric Power Research Institute (EPRI) EL-2620, Final Report,1982: 1-200.
[14] Boggs S A. Sulphur hexafluoride: introduction to the material and dielectric[J]. IEEE Electrical Insulation Magazine, 1989, 5(5): 18-21.
[15] Hagelaar G J M, Pitchford L C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J]. Plasma Sources Science and Technology, 2005, 14(4): 722-733.
[16] Hodnebrog O, Etminan M, Fuglestvedt J S, et al.Global warming potentials and radiative efficiencies of halocarbons and related compounds: a comprehensive review[J]. Reviews of Geophysics,2013, 51(2): 300-378.
[17] Hochberg B M, Sandberg E Y. Investigation of the disruptive strength of gases[J]. Journal of Technology Physics (USSR), 1942, 12(2-3): 65-75.
[18] Wilson W A, Simons J H, Brice T J. The dielectric strength of gaseous fluorocarbons[J]. Journal of Applied Physics, 1950, 21: 203-205.
[19] Heylen A E D, Lewis T J. The electrical strength of hydrocarbon gases[J]. British Journal of Applied Physics, 1956, 7: 411-415.
[20] Narbut P, Berg D, Works C N, et al. Factors controlling electric strength of gaseous insulation[J].Transactions of the American Institute of Electrical Engineers Part III: Power Apparatus & Systems, 1959,78(3): 545-550.
[21] Mason J H. Disharges[J]. IEEE Transactions on Electrical Insulation, 1978, EI-13(4): 211-238.
[22] Cooke C M, Cookson A H. The nature and practice of gases as electrical insulators[J]. IEEE Transactions on Electrical Insulation, 1978, EI-13(4): 239-248.
[23] Vijh A K. Correlation between electric strengths and heats of atomization of gaseous dielectrics[J]. Journal of Materials Science, 1976, 11(4): 784-785.
[24] Vijh A K. Intermolecular bonding and the electric strengths of dielectric gases[J]. Journal of Materials Science, 1976, 11(7): 1374-1375.
[25] Vijh A K. Communication on the relative electric strengths and the molecular weights of gases[J]. IEEE Transactions on Electrical Insulation, 1982, EI-17(1):84-87.
[26] Paul J C, Saha T N, Chakravarty B. On the gaseous breakdown[J]. Indian Journal of Physics, 1974, 48(2):138-142.
[27] Brand K P, Kopainsky J. Breakdown field strength of unitary attaching gases and gas mixtures[J]. Applied Physics, 1979, 18(4): 321-333.
[28] Brand K P. Dielectric strength, boiling point and toxicity of gases-different aspects of the same basic molecular properties[J]. IEEE Transactions on Electrical Insulation, 1982, EI-17(5): 451-456.
[29] Meurice N. Sandre E, Aslanides A, et al. Simple theoretical estimation of the dielectric strength of gases[J]. IEEE Transactions on Dielectrics &Electrical Insulation, 2004, 11(6): 946-948.
[30] Olivet A, Duque D, Vega L F. Analysis of electron interactions in dielectric gases[J]. Journal of Applied Physics, 2007, 101(1): 15-34.
[31] Rabie M, Dahl D A, Donald S M A, et al. Predictors for gases of high electrical strength[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2013, 20(3): 856-863.
[32] Zhang Chaohai, Shi Huixuan, Cheng Lin, et al. First principles based computational scheme for designing new SF6 replacements[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(5):2572-2578.
[33] Yu Xiaojuan, Hou Hua, Wang Baoshan. Prediction on dielectric strength and boiling point of gaseous molecules for replacement of SF6[J]. Journal of Computational Chemistry, 2017, 38(10): 721-729.
[34] Politzer P, Murray J S. Computational prediction of condensed phase properties from statistical characterization of molecular surface electrostatic potentials[J]. Fluid Phase Equilibria, 2001, 185(1):129-137.
[35] Rienstra-Kiracofe J C, Tschumper G S, Schaefer H F, et al. Atomic and molecular electron affinities: photoelectron experiments and theoretical computations[J]. Chemical Reviews, 2002, 102(1): 231-282.
[36] Anderson L N, Oviedo M Belén, Wong B M. Accurate electron affinities and orbital energies of anions from a nonempirically tuned range-separated density functional theory approach[J]. Journal of Chemical Theory and Computation, 2017, 13(4): 1656-1666.
[37] Bozkaya U, Unal A. State-of-the-art computations of vertical ionization potentials with the extended koopmans' theorem integrated with the CCSD(T)method[J]. Journal of Physical Chemistry A, 2018,122(17): 4375-4380.
[38] Soyda E, Bozkaya U. Assessment of orbital-optimized MP2.5 for thermochemistry and kinetics: dramatic failures of standard perturbation theory approaches for aromatic bond dissociation energies and barrier heights of radical reactions[J]. Journal of Chemical Theory and Computation, 2015, 11(4): 1564-1573.
[39] Eisfeld W. Highly accurate determination of the electron affinity of SF6 and analysis of structure and photodetachment spectrum of SF6[J]. Journal of Chemical Physics, 2011, 134(5): 054303(1-13).
[40] Troe J, Miller T M, Viggiano A A. Communication:Revised electron affinity of SF6 from kinetic data[J].Journal of Chemical Physics, 2012, 136(12): 244305(1-3).
[41] Menk S, Das S, Blaum K, et al. Vibrational autodetachment of sulfur hexafluoride anions at its long-lifetime limit[J]. Physical Review A, 2014, 89(2):022502/1-5.
[42] Olivet A, Duque D, Vega L F. Analysis of electron interactions in dielectric gases[J]. Journal of Applied Physics, 2007, 101(2): 023308(1-7).
[43] 侯华, 余小娟, 周文俊, 等. 绝缘气体介电强度的构效关系[J]. 高等学校化学学报, 2018, 39(11):2477-2484.Hou Hua, Yu Xiaojuan, Zhou Wenjun, et al.Theoretical investigations on the structure-activity relationship to the dielectric strength of the insulation gases[J]. Chemical Journal of Chinese Universities,2018, 39(11): 2477-2484.
[44] Yu Xiaojuan, Hou Hua, Wang Baoshan. A priori theoretical model for discovery of environmentally sustainable perfluorinated compounds[J]. Journal of Physical Chemistry A, 2018, 122(13): 3462-3469.
[45] 李冰, 肖登明, 赵谡, 等. 第二代气体绝缘输电线路的温升数值计算[J]. 电工技术学报, 2017, 32(13):271-276.Li Bing, Xiao Dengming, Zhao Su, et al. Temperature rise numerical calculation of the second generation gas insulated transmission line[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 271-276.
[46] 林林, 陈庆国, 程嵩, 等. 基于密度泛函理论的SF6潜在可替代性气体介电性能分析[J]. 电工技术学报, 2018, 33(18): 4382-4388.Lin Lin, Chen Qingguo, Cheng Song, et al. The analysis of SF6 potential alternative gas dielectric strength based on density functional theory[J].Transactions of China Electrotechnical Society, 2018,33(18): 4382-4388.
[47] 张晓星, 田双双, 肖淞, 等. SF6替代气体研究现状综述[J]. 电工技术学报, 2018, 33(12): 2883-2893.Zhang Xiaoxing, Tian Shuangshuang, Xiao Song, et al.A review study of SF6 substitute gases[J].Transactions of China Electrotechnical Society, 2018,33(12): 2883-2893.
[48] 邓云坤, 马仪, 赵谡, 等. 基于电子输运参数的CF3I及CF3I-N2混合气体绝缘性能分析[J]. 电工技术学报, 2018, 33(7): 1641-1651.Deng Yunkun, Ma Yi, Zhao Su, et al. Analysis of the insulation properties of CF3I and CF3I-N2 gas mixtures from electron transport parameters[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1641-1651.
[49] 李康, 郭润睿, 张国强. 一种 SF6替代气体—氟碳气体的故障分解气体产生规律及基于分解物气体的故障判据研究[J]. 电工技术学报, 2019, 34(12):2649-2656.Li Kang, Guo Runrui, Zhang Guoqiang. Study on fault decomposition properties and fault diagnostic criterion of fluorocarbon gas-a substitute gas for SF6[J]. Transactions of China Electrotechnical Society,2019, 34(12): 2649-2656.
[50] 彭敏, 王宝山, 于萍, 等. 六氟化硫替代气体三氟化硫氮的制备及表征[J]. 应用化工, 2018, 47(11):2301-2303.Peng Min, Wang Baoshan, Yu Ping, et al. Preparation and characterization of NSF3 for the alternative gas of SF6[J]. Applied Chemical Industry, 2018, 47(11):2301-2303.
[51] 王易, 高克利, 王宝山, 等. 一种由三氟甲基磺酰氯制备三氟甲基磺酰氟的方法: 中国, 109824551A[P].2019-05-31.