0 引言
模块化多电平换流器（Modular Multilevel Converter，MMC）克服了传统两电平或三电平电压源换流器应用于高压领域需要大量电力电子开关器件串联的缺点，显著降低了对电力电子开关器件一致性及动静态均压性能的要求[1-3]。自 2010年世界上第一个基于MMC的柔性直流输电系统——Trans Bay Cable工程投入运行以来，模块化多电平高压直流输电（High Voltage Direct Current Transmission based MMC, MMC-HVDC）系统发展迅速，已投运和在建的相关工程达数十项[4-5]。
不同于基于同步发电机的常规电源，基于电力电子器件的柔性直流换流站具有高度的可控性，其交流侧故障特征受所采用的控制策略、控制参数、控制目标等因素影响。此外，受电力电子器件过电流能力的限制，交流电网故障时柔性直流换流站输出电流相比于常规电源增幅较小。常规同步电源与柔性直流换流站故障特征差异较大，基于常规同步电源故障特征设计的继电保护在柔性直流换流站接入后可能存在适应性问题。选相元件是距离保护和自动重合闸故障相识别的核心元件，其正确性是距离保护和自动重合闸能正确动作的基础和前提[6]。因此，研究柔性直流换流站接入对传统选相方法的影响并提出相应的解决措施对于保障电力系统的安全稳定运行具有重要意义。
柔性直流输电系统在各种工况下的控制策略一直是学术界的研究热点，国内外相关研究成果较多。文献[7-9]提出了电网电压不对称时MMC-HVDC的控制策略并进行了验证。文献[10-11]分析了 MMC上、下桥臂电感不对称时，MMC-HVDC交流侧电流和环流成分，并提出抑制基频和二倍频环流及保证桥臂直流电压平衡的控制策略。文献[12-13]分析了弱交流系统下柔性直流输电系统控制的稳定性问题，并提出能适应弱交流电网的控制策略。尽管柔性直流输电系统控制策略的研究较为成熟，但柔性直流换流站接入后对交流电网继电保护的相关研究成果极少。文献[14]指出柔性直流输电系统可能导致区内故障负序方向元件误动，但未研究对传统选相方法的影响。除文献[14]外，鲜有文献研究柔性直流输电系统对继电保护的影响。国内已有部分学者研究新能源电站接入对传统选相方法的影响，并给出一些结论[15-16]。但新能源电站接入对传统选相方法影响的研究结论是否适用于柔性直流输电系统还需进一步探究，并且已有的研究并未从故障电流解析表达式的角度深入分析对传统选相方法的影响机理。文献[17]深入分析了基于晶闸管的常规直流输电逆变侧换相失败对传统选相方法的影响。但柔性直流输电系统不存在换相失败问题，相关研究结论并不适用。
本文首先研究了换流变压器阀侧Y形联结和D接时交流输电线路换流站侧的故障电流特征；然后从理论上分析了相电流差突变量选相方法和电流序分量选相方法的适应性问题；为此提出了一种基于保护安装处电压序分量的选相方法，详细阐述了该选相方法的原理和选相流程；最后在PSCAD/EMTDC中对传统选相方法的适应性和本文所提选相方法的有效性进行了仿真验证。
1 换流变压器网侧故障电流特性分析
图1为MMC-HVDC换流站接入电网的示意图。MMC-HVDC换流站所接交流线路一般为高压输电线路，因此换流变压器网侧一般采用Y形联结且中性点直接接地。为了避免零序电流流入阀侧，换流变压器阀侧一般有两种接线形式:①Y形联结（鲁西背靠背直流异步联网工程采用此接线方式），中性点经高阻接地；②D形联结（舟山多端直流输电工程定海换流站采用此联结方式[18]），此时阀侧一般采用星形联结电抗器构成辅助接地中性点。对于第①种联结方式，输电线路发生接地故障时，由于换流变压器阀侧Y形联结绕组中性点接地高阻对零序电流的阻碍作用，导致无法产生零序电流，则换流站侧（M侧）故障电流不含零序分量。对于第②种联结方式，输电线路发生接地故障时，由于阀侧D形联结绕组能为零序电流提供通路，因此，换流站侧（M侧）故障电流含有零序分量。由图1，M侧为换流站侧，N侧为电网侧（常规电源侧）。N侧的故障电流特征主要由基于同步发电机的电网决定，传统的选相方法能正确动作。因此本文主要分析MMCHVDC换流站接入对交流输电线路换流站侧（M侧）传统选相方法动作性能的影响。为了研究M侧传统选相方法的适应性问题，需要首先深入分析交流输电线路换流站侧（M侧）故障电流特性。下面将根据换流变压器阀侧联结方式分两种情况进行讨论。
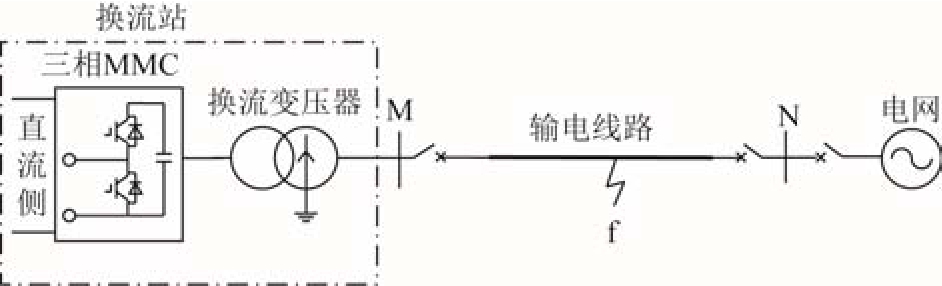
图1 MMC-HVDC换流站接入电网示意图
Fig.1 Diagram of power grid connected with MMCHVDC station
1.1 换流变压器阀侧Y形联结时M侧故障电流特性分析
为了避免零序电流流入换流变压器阀侧，换流变压器阀侧中性点经高阻接地。交流输电线路发生短路故障后，不考虑零序分量，阀侧电压表达式为
式中，U为电压幅值；上标“+”“-”分别表示正、负序分量；ω1为电网额定角频率；以正序电压为相位基准，因此正序电压初相角为 0°，负序电压初相角为δ。
电网电压不对称时，存在负序电压，并引起负序电流，导致三相电流不对称且有功和无功功率出现二倍频波动分量。抑制负序电流、抑制有功波动和抑制无功波动三种控制目标相互矛盾，只能实现其中一种，对应的αβ坐标系下通用指令电流表达式为[19]
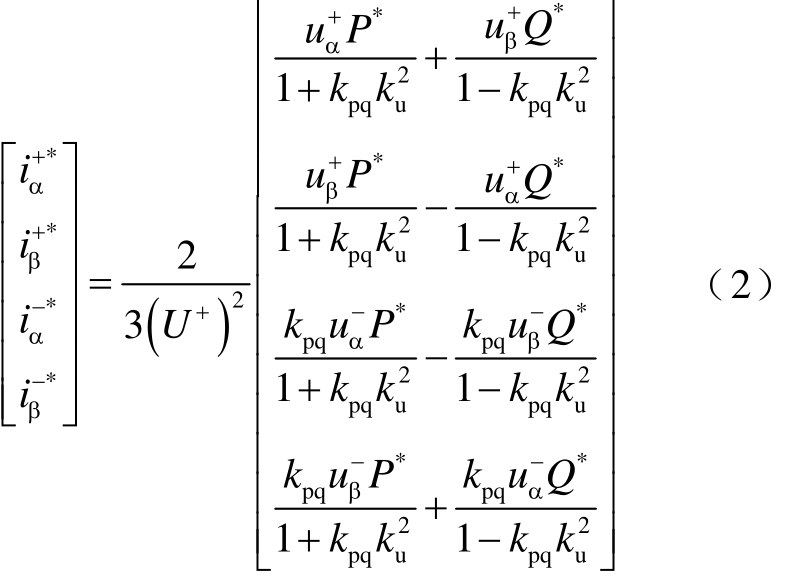
式中，P*和Q*分别为有功和无功的指令值；ku为电网电压不平衡度，ku=U U- +；kpq为调节系数，kpq=-1时抑制有功波动（控制目标 1），kpq=0时抑制负序电流（控制目标2），kpq=1时抑制无功波动（控制目标3）。
采用工程上常用的双矢量控制或静止坐标下的比例谐振控制器等控制方法可以保证 MMC-HVDC阀侧电流迅速跟踪上其指令电流，并且稳态误差很小。因此，根据式（2）可得故障期间阀侧三相电流的解析表达式为
式中
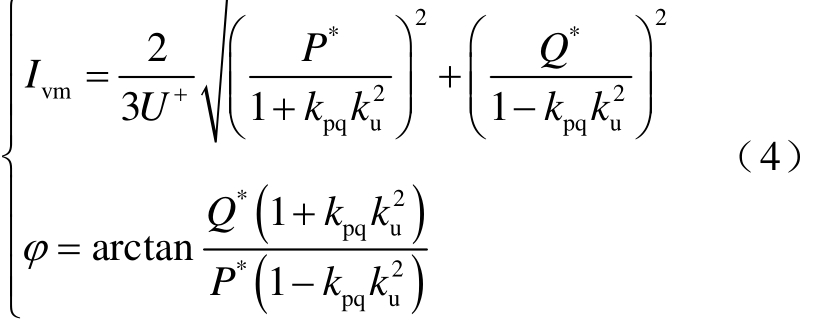
由于阀侧中性点经高阻接地，零序电流没有流通通路，因此M侧电流不含零序分量，则M侧电流为
式中，kt为换流变压器电压比。
根据式（3）~ 式（5），换流变压器阀侧为Y形联结且中性点经高阻接地时，M侧的故障电流由正序和负序分量组成，理论上三相故障电流的幅值和不对称程度与有功指令、无功指令、控制目标、电网电压不平衡度等因素相关。由于受电力电子开关器件过电流能力的限制，M侧故障电流的最大值一般与额定值相差不大。
1.2 换流变压器阀侧D形联结时M侧故障电流特性分析
假设采用 YNd11接线，零序电流能在 D形联结内部绕组中形成环流，阀侧D形联结为零序电流提供通路，则M侧故障电流可能由正、负、零序分量组成，其一般表达式为
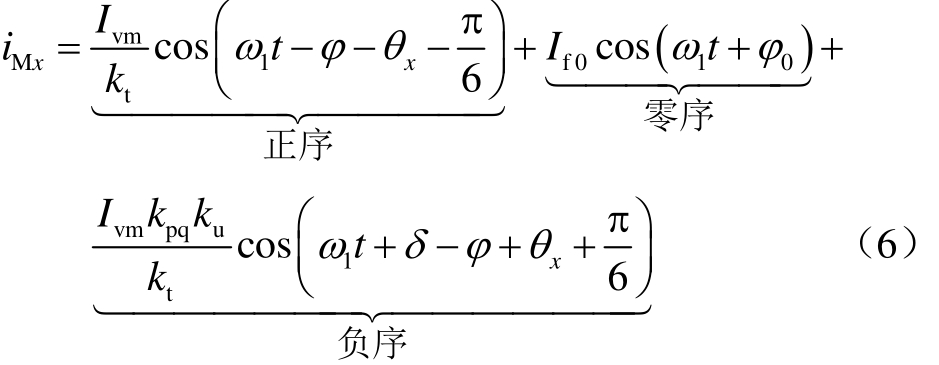
式中，
If0为零序电流幅值；φ0为零序电流相位。
交流输电线路发生接地短路故障时，M侧故障电流包含零序电流。根据前文分析，由于电力电子开关器件过电流能力的限制，故障电流的正、负序分量幅值与正常运行时的电流幅值相差并不大，等效为M侧具有很高的正、负序阻抗，MMC-HVDC换流站对于正、负序故障分量网络表现为弱馈特性。而零序回路是由线路和换流变压器组成，与MMCHVDC换流站无关。零序阻抗远小于 MMC-HVDC换流站等效正、负序阻抗，因此，M侧故障电流中零序分量一般远大于正、负序分量，故障电流以零序分量为主。
若发生非接地短路故障，则式（6）中的零序电流为零，M侧故障电流特征与换流变压器阀侧Y形联结时类似。
根据本节分析，可得出以下几点结论:
（1）与常规电源的故障电流相比，受电力电子开关器件过电流能力的限制，柔性直流换流站发出的正、负序电流幅值较小，导致换流站侧（M 侧）呈现正、负序分量的弱馈特性。
（2）发生非接地故障时，阀侧Y形和D形联结对应的M侧故障电流特性基本一致；故障电流中不含零序分量，故障电流幅值与正常运行时的电流幅值相差并不大。
（3）发生接地故障时，阀侧Y形联结且中性点经高阻接地时的故障电流不含零序分量，幅值较小；阀侧D形联结时的故障电流以零序分量为主。
2 传统选相方法适应性分析
2.1 相电流差突变量选相方法适应性分析
相电流差突变量选相方法是微机保护中常用的选相方法，其中相电流差突变量定义为
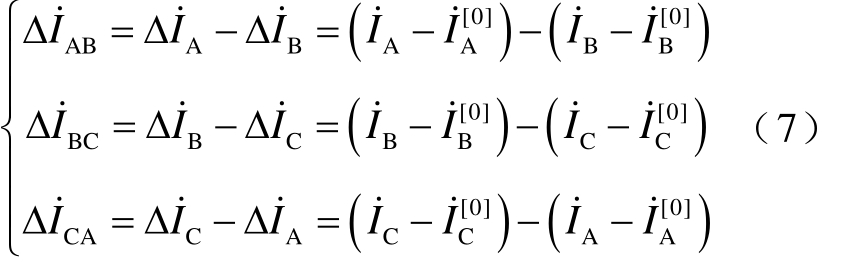
式中， I˙A、 I˙B、 I˙C为故障后电流
为故障前电流。
相电流差突变量选相方法的选相流程见附录。
本文以换流变压器阀侧 Y形联结、A相接地故障为例，分析柔性直流换流站接入对相电流突变量选相方法的影响。假设故障前三相电流相量表达式为
式中，INm为正常运行时的额定电流幅值；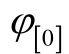
为故障前电流的初相角。
根据式（3）~式（5）及式（8）可得
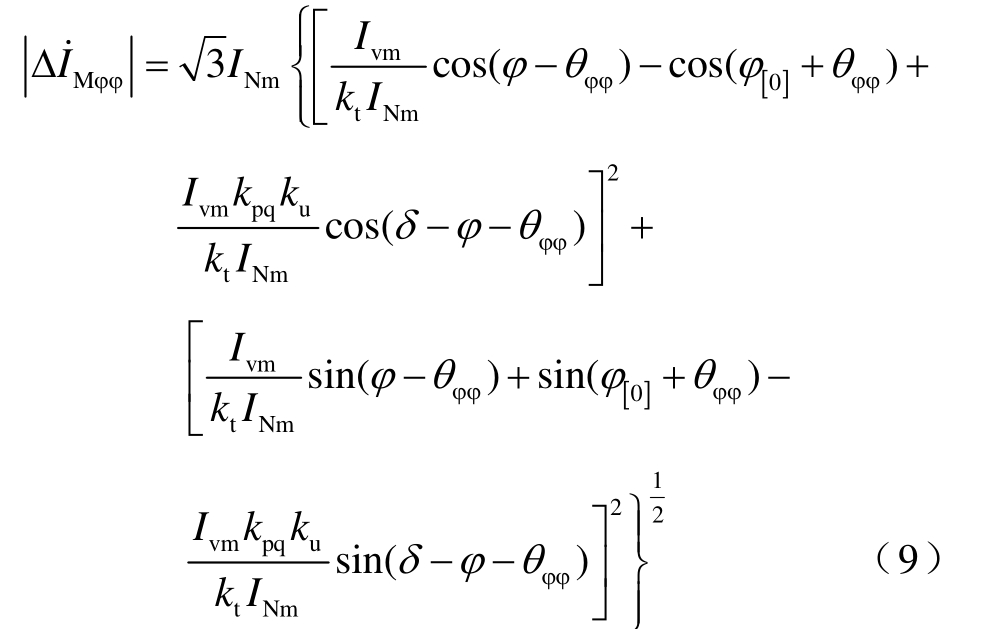
式中，下角标 φφ=AB,BC,CA；θAB=π/6, θBC=3π/2,θCA=5π/6。
根据式（4）和式（9），
这7个变量相关，极大地增加了理论分析的难度。为了便于后续分析，本文做出以下三点合理假设:①接地电阻较小，近似金属接地；②正、负、零序阻抗角近似相等，大多数已建成和在建的MMC-HVDC换流站接入的交流线路一般为高压输电线路（主要为 220kV及以上电压等级），对于高压线路电抗远大于电阻，因此，正、负、零序阻抗角基本接近90°，三者近似相等；③正、负序阻抗近似相等，零序阻抗幅值不高于正序阻抗幅值的 3倍。根据以上假设可得:
2/3(pu)≤U+≤4/5(pu)；1/4＜ku≤1/2。
图2给出了U+、ku和控制目标变化时相电流差突变量幅值比。其中，P*=0.7(pu)，Q*=0.4(pu)。采用控制目标2时（抑制负序电流），无论正序电压幅值U+和电压不平衡度 ku如何变化，三个相电流差突变量幅值始终相等，即
采用另外两个控制目标时，相电流差突变量幅值比随着正序电压幅值U+和电压不平衡度 ku的变化而变化。由图 2，两个相电流差突变量幅值比
最大值均小于1.5，显然不满足附录中式（A1）中判定A相接地故障的条件，导致相电流差突变量选相方法不能正确选相。
图2 相电流差突变量幅值比
Fig.2 The amplitude ratio of the phase current difference suddenly-change
本节分析了A相接地时，柔性直流换流站接入对相电流突变量选相方法的影响。其他情况的分析过程与之类似，限于篇幅，本文不再赘述。
2.2 序分量选相方法适应性分析
序分量选相方法是利用保护安装处故障电流正、负、零序分量之间的相位和幅值关系实现选相的[20]，具体的选相流程见附录。
当阀侧Y形联结且中性点经高阻接地，交流输电线路发生单相或两相接地故障时，M侧保护安装处流过的电流并不包含零序电流。根据附图 2，接地故障将被误判为非接地故障，序分量选相方法无法正确动作。
当阀侧D形联结时，根据附图3，由式（4）、式（6）和式（8）可得
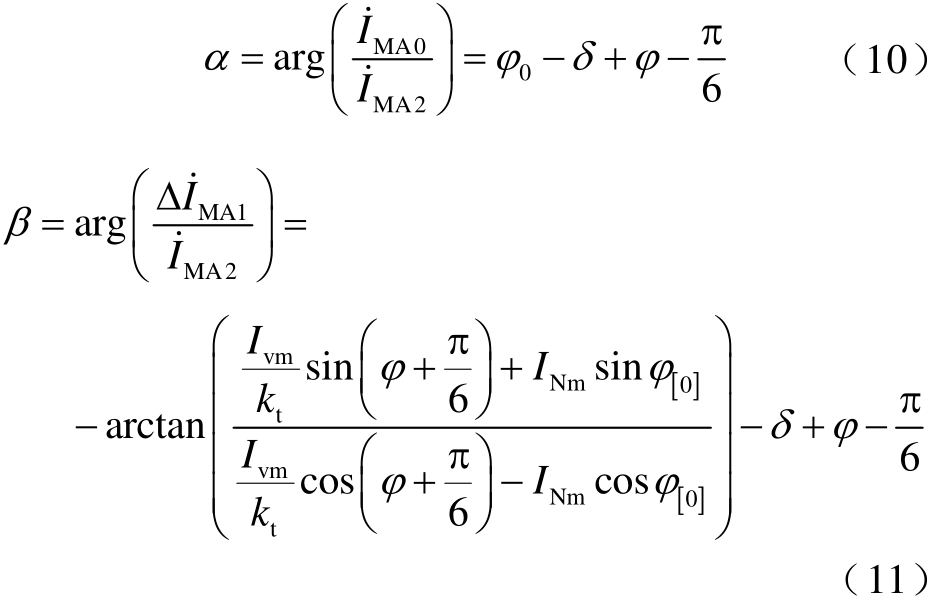
式中，MA0I˙为M侧A相零序电流；MA1IΔ˙为M侧A相正序电流故障分量； MA2I˙ 为M侧A相负序电流。
以A相接地故障为例分析序分量选相方法的适应性。根据附图3，α和β要同时满足 α∈(-30°, 30°)和β∈(-60°,0°)两个条件方能判定为A相接地故障。
若采用控制目标2（抑制负序电流），此时柔性直流换流站只输出正序电流，M 侧不含负序电流。考虑到实际采样过程可能引入噪声和误差信号，实际测量到的为一个幅值很小而相位波动较大的小信号。采用该信号计算得到的α随机性较大，可能落到任何一个故障区间，导致序分量选相方法不能正确选择故障相。
若采用控制目标1（抑制有功波动），换流站将同时输出正、负序电流。正常运行时，换流站一般只传输有功功率，则故障前电网电压与电流同相位，初相角为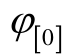
。由式（1），故障后阀侧正序电压初相角为0°，则M侧的正序电压初相角为-30°。本节仍采用2.1节的三点假设，则
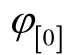≈-30°，δ≈π，2/3(pu)≤U+≤4/5(pu)；1/4＜ku≤1/2。A 相接地故障时，零序电压相位与故障前电压相位近似相等，则零序电流初相角为 φ0=φ[0]–90°。
图3给出了A相接地故障下正序电压幅值和电压不平衡度变化时对应的α和β。由图3，随着正序电压幅值和电压不平衡度的变化，α的取值范围介于 48°~55°，而 β 的取值范围介于-170°~ -140°，两者都不满足附图3中判定A相接地的条件，故而引起序分量选相方法误选相。采用控制目标 3（抑制无功波动）时的分析过程与之类似，不再赘述。
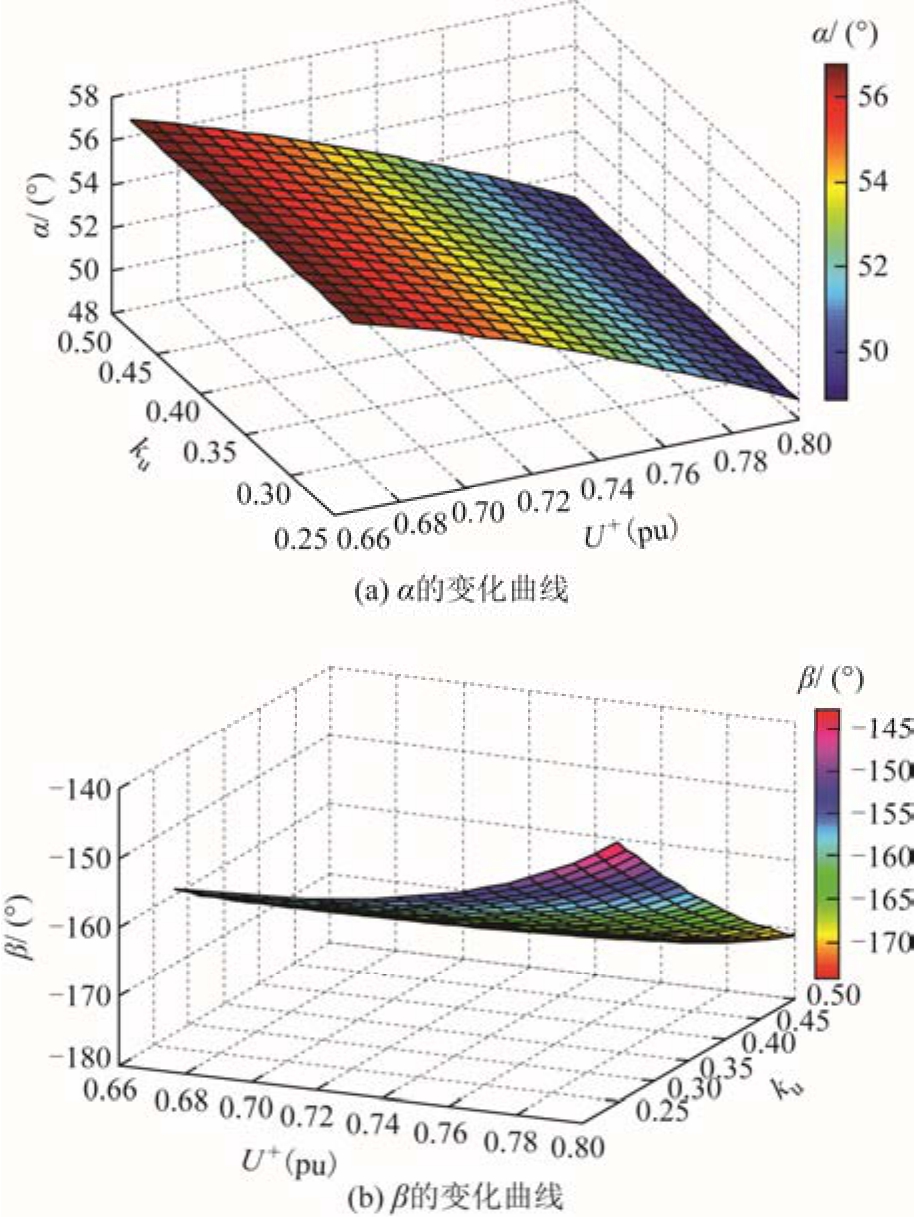
图3 正序电压幅值和电压不平衡度变化时对应的α和β变化曲线
Fig.3 The curves of α and β when magnitude of positivesequence voltage and degree of voltage unbalance change
综上所述，无论阀侧Y形联结还是D形联结，柔性直流换流站接入都可能导致序分量选相方法误选相。
3 电压序分量选相方法
根据前文分析，柔性直流换流站的故障电流特征受控制目标、控制策略、换流变压器联结方式和电力电子开关器件过电流能力等多个因素的影响，与常规同步电源的故障电流特征差别较大，导致传统的相电流差突变量选相方法和序分量选相方法可能误动作。而选相方法的正确性决定了阻抗继电器计算的准确性和自动重合闸动作的正确性，其误动作将引发继电保护和断路器的不正确动作，影响电力系统运行的安全性。为此，本节提出一种基于保护安装处电压序分量的选相方法，该选相方法的动作性能基本不受柔性直流换流站的影响。
保护安装处的故障电流受多种因素影响，但其电压与换流站的控制策略和换流变压器的联结方式相关性较小，因此本文考虑基于保护安装处正、负、零序电压的相位和幅值关系构成一种能适应柔性直流换流站的电压序分量选相方法。
3.1 保护安装处和故障点处电压序分量关系
图1所示包含柔性直流换流站的系统对应的故障序分量网络如图 4所示。图中，j=1,2,0，分别表示正、负、零序分量；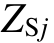
为电网的序阻抗；
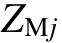和
分别为母线M、N到故障点f处的序阻抗；
为换流站的等效序阻抗；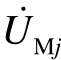
和
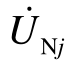分别为母线M、N的序电压；
和 
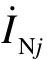分别为母线M、N流向故障点f的序电流；
和
分别为故障点处的序电压和流向故障点的序电流。
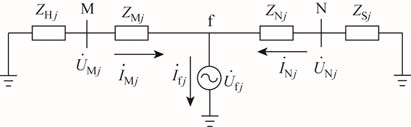
图4 柔性直流换流站接入系统的故障序分量网络
Fig.4 The fault sequence component network of MMCHVDC station integration
柔性直流换流站的等效序阻抗 ZHj的大小与控制目标、换流变压器联结方式和电力电子开关器件的过电流能力等多个因素相关。如前所述，考虑到工程造价的问题，交流系统故障期间电力电子开关器件的电流限幅值一般与正常运行时的额定电流幅值相差不大，即换流站输出的正、负序电流相比于额定电流在幅值上并没有较大的差别，则
由此可见，在正、负序故障网络中，柔性直流换流站表现为弱馈特性，即
由此可得
ZH0与换流变压器的联结方式有关，阀侧 Y形联结且中性点经高阻接地时，零序电流在M侧没有通路，零序阻抗近似无穷大，即ZH0=∞，此时
阀侧 D形联结时，零序电流能在 M侧流通，ZH0即为换流变压器漏抗，此时
。因此，母线M处零序电压幅值和故障点f处的零序电压幅值关系为
3.2 基于保护安装处电压序分量的新型选相方法
根据 3.1节的分析，保护安装处的正、负序电流与流入故障点的正、负序电流差别很大，但保护安装处的正、负序电压与故障点处的正、负序电压差别很小。此外，柔性直流换流站并不输出零序电流，对保护安装处零序电压的影响较小。因此，为了能适应含柔性直流换流站的电力系统，本文考虑基于保护安装处正、负、零序电压分量的幅值和相位关系进行故障选相。
电力系统的短路故障包括四种:单相接地故障、两相短路故障、两相接地故障和三相短路故障。
1）三相短路故障的判定
判定三相短路故障只需两个条件:①保护安装处零序电压为零；②保护安装处负序电压为零。
2）两相短路故障相的判定
要判定两相短路的故障相需要三个条件:①保护安装处零序电压为零；②保护安装处负序电压不为零；③依据保护安装处正序电压与负序电压的相位关系判别具体的故障相。
定义 γphase为
相间短路相量及故障分区如图5所示，BC相间短路、AB相间短路和CA相间短路对应故障点f处 A相正序电压与 A相负序电压的相位差arg(fA1U˙ /fA2U˙ )分别为 0°、120°和-120°。根据式（13）和式（15）可得
如图5所示，考虑到测量误差、过渡电阻及正负序故障电流对相位误差影响等因素，设定 γphase若在区间[-60°,60°)、[60°,180°)、[-180°,-60°)内，分别判定为 BC相间短路、AB相间短路和CA相间短路。
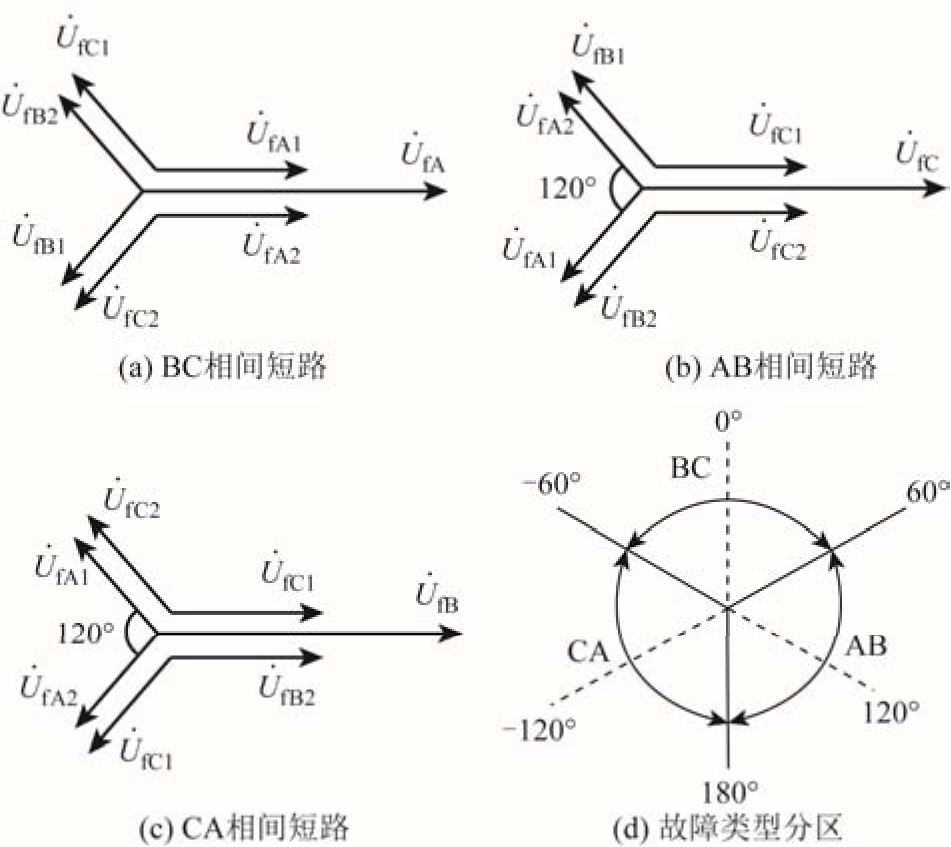
图5 相间短路相量及故障分区
Fig. 5 Phasor diagram of phase-to-phase fault and fault partitions diagram
3）单相接地故障相的判定
单相接地故障相的判定需要三个条件:①保护安装处零序电压不为零，以此判定为接地故障；②根据正、负、零序电压的幅值区分单相接地故障和两相接地故障；③根据保护安装处正序电压与负序电压的相位关系判别具体的故障相。
当发生A相金属接地故障时，可得出故障点f 处的正、负、零序电压满足
根据式（13）、式（14）和式（17）可得
根据三相正、负、零序电压幅值的关系，发生B相或C相接地故障时，式（18）的关系仍然成立。
当发生 BC两相金属接地故障时，可得出故障点f处的正、负、零序电压满足
根据式（13）、式（14）和式（19）可得
发生AB两相接地或CA两相接地时，式（20）的关系仍然成立。
对比式（18）和式（20），单相接地故障时的γmag和两相接地故障时的γmag在数值上差距非常大，可以通过 γmag的数值很容易区分单相接地和两相接地，该判定条件灵敏度高。γmag≤1判定为单相接地故障，γmag＞1判定为两相接地故障。
单相接地故障相量及故障分区如图6所示，发生A相接地、B相接地、C相接地时γphase分别近似为180°、60°和-60°，分别对应的故障相判定区间为[120°,180°)U[-180°,-120°)、[0°,120°)、[-120°, 0°)。
图6 单相接地故障相量及故障分区
Fig. 6 Phasor diagram of single phase-to-ground fault and fault partitions diagram
4）两相接地故障相的判定
单相接地故障相的判定需要三个条件:①保护安装处零序电压不为零，以此判定为接地故障；②γmag＞1判定为两相接地故障；③根据保护安装处正序电压与负序电压的相位关系判别具体的故障相。
两相接地故障，故障点正序电压与负序电压的相位关系与相间短路类似，可参照图 5，本文不再给出相应的相量图及故障分区图。发生BC两相接地、AB两相接地、CA两相接地时 γphase分别近似为 0°、120°和-120°，分别对应的故障相判定区间为[-60°,60°)、[60°,180°)、[-180°,-60°)。
基于保护安装处正、负、零序电压分量幅值和相位关系的选相方法的选相流程如图7所示。
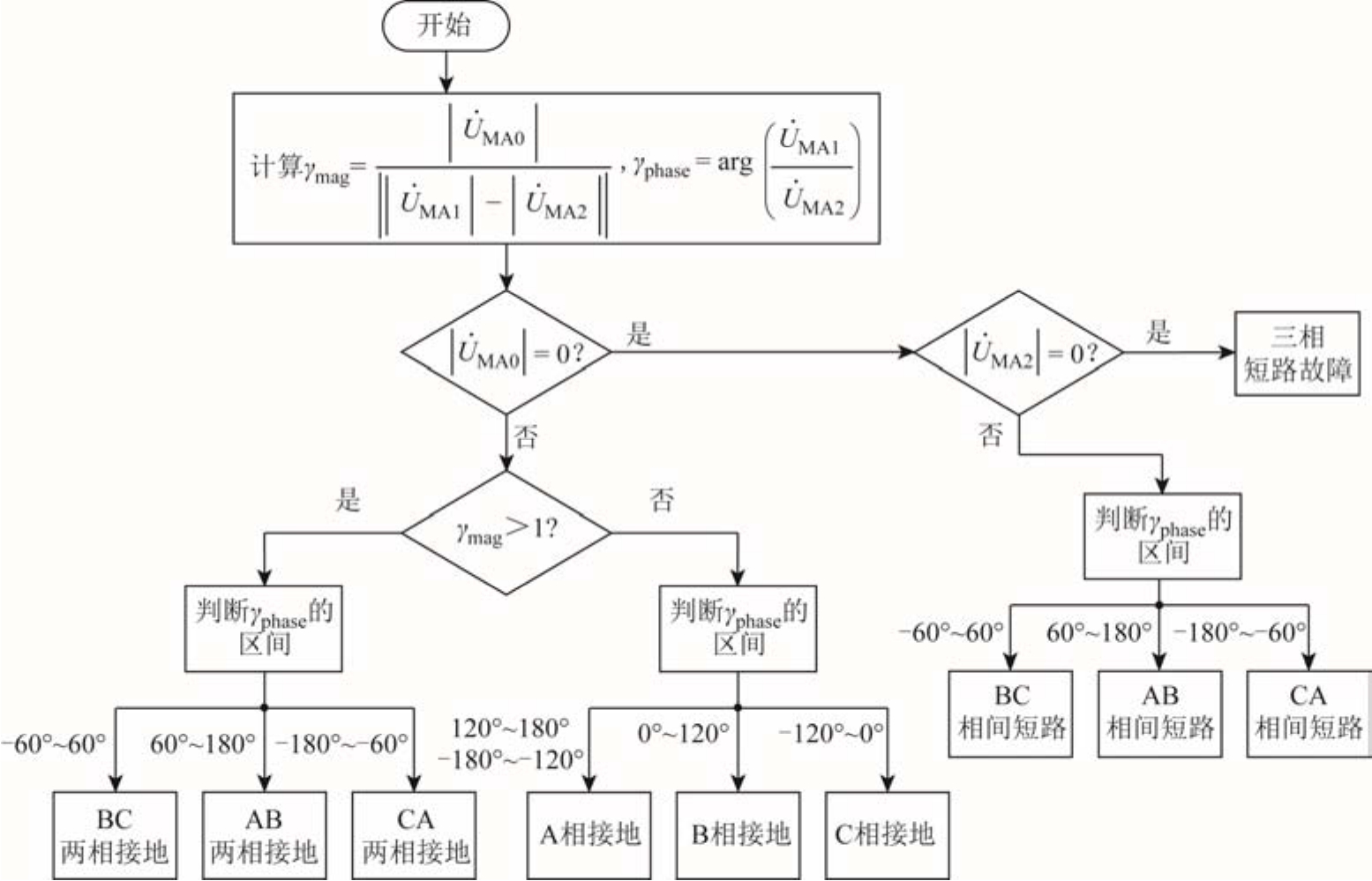
图7 电压序分量选相方法的选相流程
Fig. 7 The flow chart of phase selection method based on voltage sequence component
4 仿真分析
为了验证本文对传统选相方法理论分析的正确性及所提电压序分量选相方法的有效性，在PSCAD/EMTDC中搭建双端MMC-HVDC模型，单侧的示意图如图1所示。仿真模型参数如下:换流站额定容量为 1 000MW；桥臂电抗器的电感值为105mH；子模块电容为 8 000μF；直流侧电压为700kV；换流变压器电压比为525/375kV，短路阻抗14%；交流输电线路 300km，正序、零序阻抗分别为(0.02+j0.28)Ω/km、(0.065+j0.728) Ω/km，正序、零序电容分别为 0.013μF/km、0.008 7μF/km；系统等值正序和零序阻抗分别为(0.520 3+j5.947 2)Ω、(1.893 8+j15.424 2)Ω。
图8给出了电网发生单相接地故障时，三种控制目标对应的仿真结果。有功指令值为600MW，无功指令值为200Mvar。由图8可以看出，采用抑制有功波动或抑制无功波动的控制目标时，柔性直流换流站输出的交流电流三相不对称，并且电流最大值明显高于采用抑制负序电流控制目标时的电流最大值。因此，在相同的有功和无功指令值下，采用抑制负序电流的控制目标能提高电力电子器件运行的安全性。在电力电子器件过电流能力的限制下，采用抑制负序电流的控制目标，可以传输更多的有功功率和无功功率。因而实际柔性直流输电系统一般采用抑制负序电流的控制目标，极少采用另外两种控制目标，故本节主要测试在抑制负序电流控制目标下柔性直流换流站对选相方法的影响。
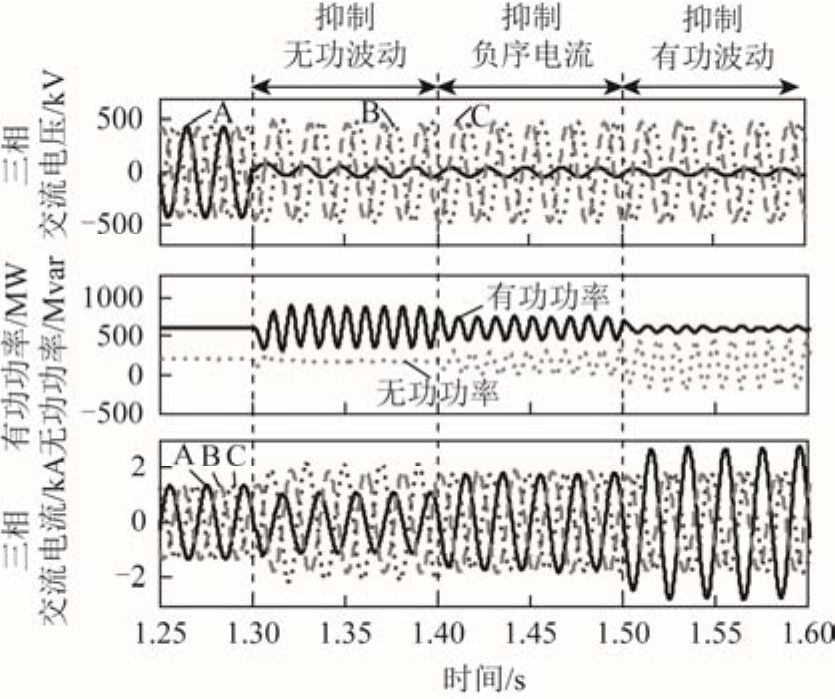
图8 控制目标切换时的仿真结果
Fig. 8 Simulation results of switching control targets
1.3 s时刻，交流输电线路中点发生A相接地故障，不同接线方式下的故障电流波形如图9所示，其中过渡电阻为 30Ω。图 9a为换流变压器阀侧 Y形联结且中性点经大电阻接地时的故障电流波形；图9b为换流变压器阀侧D形联结时的故障电流波形。对比图9a和图9b，阀侧三相电流波形特征基本一致，只包含正序电流分量，两种联结方式都可以避免零序电流流向柔性直流换流站阀侧；阀侧Y形联结时，M侧电流不含零序分量，以正序分量为主；阀侧 D形联结时，M侧三相电流以零序分量为主。以上故障电流特征与第1节的理论分析结果一致。
图9 不同接线方式下的故障电流波形
Fig. 9 Fault current waveforms under different connection mode
为了测试柔性直流换流站对传统选相方法的影响及验证本文选相方法的有效性，在各种故障类型下进行多组仿真测试，测试结果见表 1，其中过渡电阻为5Ω。表1给出了交流输电线路中点发生各种类型故障下传统相电流差突变量选相方法、电流序分量选相方法和本文所提选相方法的选相结果。仿真算例中，采样率为2kHz。
由图9，换流变压器阀侧联结方式影响M侧的故障电流波形，进而使得 Y形联结和 D形联结方式下同一选相方法的故障相判别结果不一致。但无论阀侧是 Y形联结还是 D形联结，大部分故障情况下，两种传统选相方法都无法正确判别故障类型和故障相。由表1，采用本文所提基于电压序分量选相方法时，在各种故障情况下，都能准确判别故障类型和故障相别，为距离保护和自动重合闸的正确动作提供保障。
表1 交流输电线路中点发生各种类型故障下选相方法的选相结果
Tab.1 Results of phase selection method for all types of fault in the middle of AC transmission line
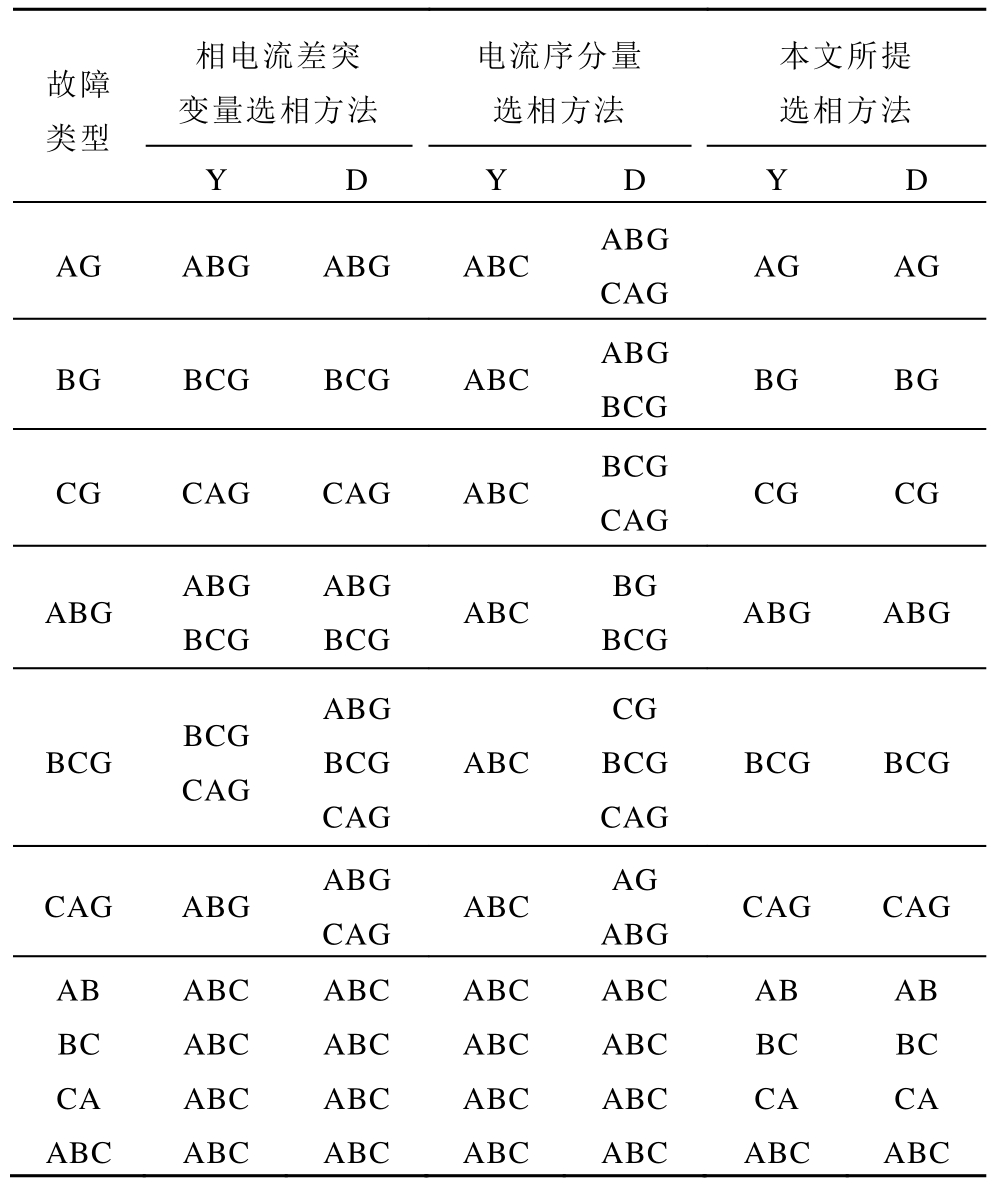
故障类型相电流差突变量选相方法电流序分量选相方法本文所提选相方法Y D Y D Y D AG ABG ABG ABC ABG CAG AG AG BG BCG BCG ABC ABG BCG BG BG CG CAG CAG ABC BCG CAG CG CG ABG ABG BCG ABG BCG ABC BG BCG ABG ABG BCG BCG CAG ABG BCG CAG ABC CG BCG CAG BCG BCG CAG ABG ABG CAG ABC AG ABG CAG CAG AB ABC ABC ABC ABC AB AB BC ABC ABC ABC ABC BC BC CA ABC ABC ABC ABC CA CA ABC ABC ABC ABC ABC ABC ABC
表1已经证实不同故障类型、阀侧不同联结方式下，本文所提选相方法能正确选择故障相。本文将进一步验证不同过渡电阻下所提选相方法的有效性。在阀侧为D形联结情况下，以单相接地故障（A相接地）和相间短路故障为例（BC相间短路）进行验证。表2给出了不同过渡电阻下，A相接地故障和BC相间短路时，本文所提选相方法在换流站侧（M侧）和常规电源侧（N侧）的选相结果。由表2可以看出，本文所提基于电压序分量的选相方法在不同过渡电阻下，仍能准确地选择故障相。本文所提选相方法不仅适用于接入柔性直流换流站的交流线路，同时还适用于接入常规同步电源的交流线路。
图10给出交流线路经10Ω过渡电阻发生C相接地故障时采用本文所提选相方法得到的仿真结果。发生接地故障时，零序电压分量不为零，由此可判定为接地故障。由图10，γmag＜1，根据选相流程图 7，判定为单相接地故障。由于 γphase介于-120°~0°，根据图7所示的选相流程，可进一步判定为C相接地故障，选相正确。由图10，1.5s发生C相接地故障后，γmag始终小于1，γphase在不到10ms的时间进入到-120°~0°区域，因此，本次故障相判定的时间小于10ms。除C相接地故障以外，对其他故障类型进行大量仿真，本文所提选相方法的响应时间一般不超过20ms。
表2 不同过渡电阻下本文所提选相方法的选相结果
Tab.2 Results of the proposed phase selection method under different fault resistance
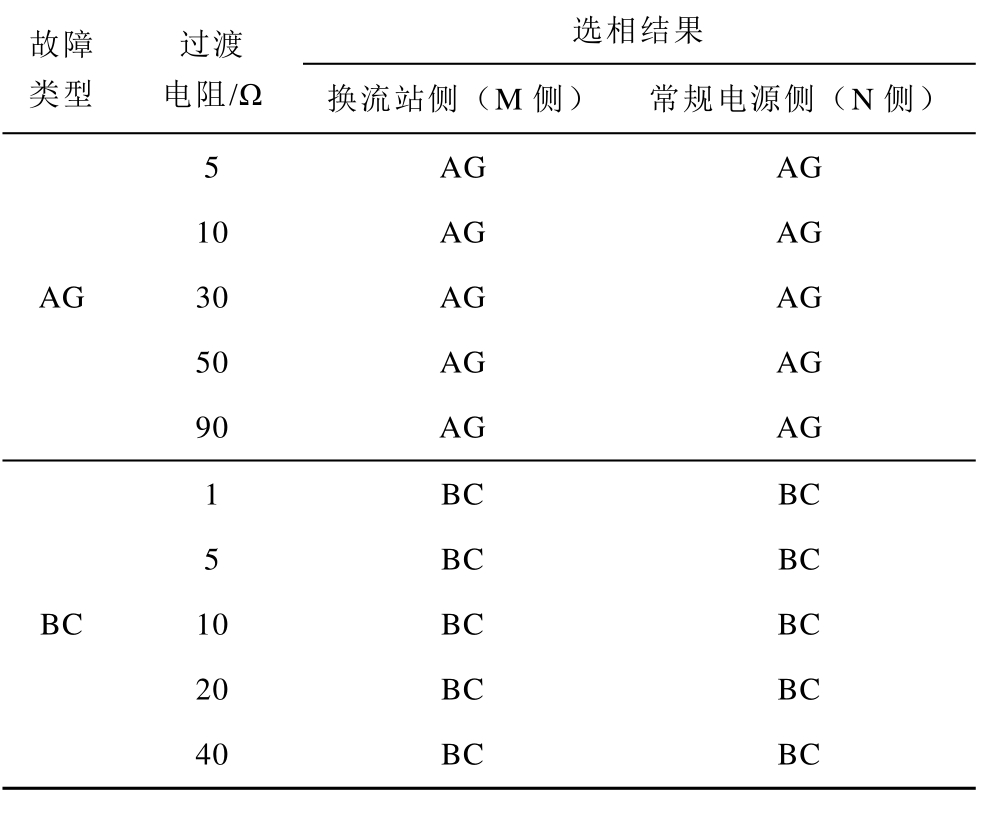
故障类型过渡电阻/Ω选相结果换流站侧（M侧） 常规电源侧（N侧）5 AG AG AG 10 AG AG 30 AG AG 50 AG AG 90 AG AG 1 BC BC BC 5 BC BC 10 BC BC 20 BC BC 40 BC BC
图10 C相接地故障时的仿真结果
Fig. 10 Simulation results under phase C to ground fault
5 结论
本文研究了换流变压器阀侧不同联结方式下换流站侧（图1中M侧）的故障电流特征，据此从理论上分析了传统的相电流差突变量选相方法和电流序分量选相方法的适应性问题，并进行了仿真测试，得出以下几点结论:
1）相比常规同步电源，受限于电力电开关器件的过电流能力，柔性直流换流站呈现正、负序分量的弱馈特性。
2）换流变压器阀侧接线方式影响接地故障下换流站侧的故障电流特征:Y形联结时没有零序电流，D形联结时含有零序电流，进而导致不同联结方式下同一选相方法的故障判别结果不一致。
3）多数故障类型下，安装在柔性直流换流站侧的两种传统选相方法无法正确识别故障类别和故障相。
4）无论交流输电线路接入柔性直流换流站还是常规电源，本文所提选相方法均能够准确识别故障类别和故障相。
附 录
相电流差突变量选相方法的选相流程如附图1所示；电流序分量选相方法选相流程如附图 2所示；序分量选相方法分区示意图如附图3所示。
附图1 相电流差突变量选相方法选相流程
App.Fig.1 The flow chart of phase selection method based on the phase current difference suddenly-change
附图2 电流序分量选相方法选相流程
App.Fig.2 The flow chart of phase selection method based on current sequence component
附图1中式（A1）、式（A2）为
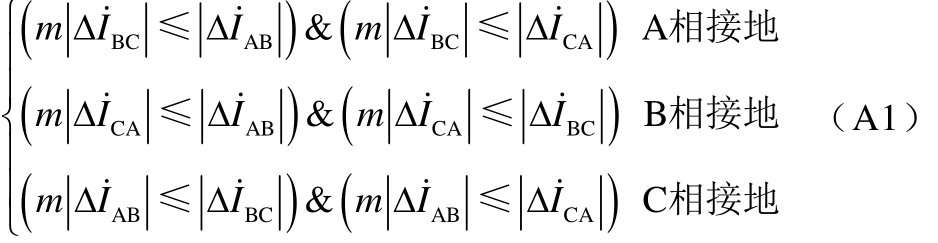
附图3 序分量选相方法故障分区
App.Fig.3 Fault partitions of two sequence component phase selection method
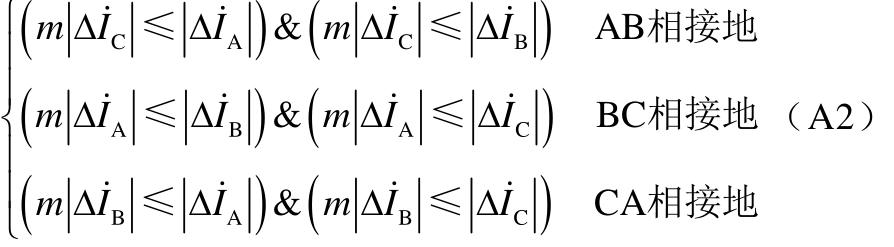
式中，m一般取4~8。
[1] Yang Qichen, Qin Jiangchao, Saeedifard M．A postfault strategy to control the modular multilevel converter under submodule failure[J]. IEEE Transactions on Power Delivery, 2016, 31(6): 2453-2463.
[2] 王洁聪, 刘崇茹, 徐东旭, 等. 基于 RTDS的模块化多电平换流器闭锁状态仿真建模方法[J]. 电工技术学报, 2018, 33(16): 3686-3696.Wang Jiecong, Liu Congru, Xu Dongxu, et al.Simulation method of modular multilevel converter blocking state based on RTDS[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3686-3696.
[3] 郝亮亮, 张静, 顾亚旗, 等. 基于桥臂能量预测的模块化多电平换流器子模块故障优化容错控制策略[J]. 电工技术学报, 2018, 33(16): 3697-3706.Hao Liangliang, Zhang Jing, Gu Yaqi, et al. Submodule fault tolerant optimal control strategy of modular multilevel converter based on estimation of bridge energy[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3697-3706.
[4] 邹常跃, 陈俊, 许树楷, 等. 长控制链路延时特征下柔性直流输电系统动态性能改善方法[J]. 电网技术, 2017, 41(10): 3216-3222.Zou Changyue, Chen Jun, Xu Shukai, et al. Dynamic performance optimization of VSC-HVDC considering its long delay[J]. Power System Technology, 2017,41(10): 3216-3222.
[5] 陈继开, 孙川, 李国庆, 等. 双极 MMC-HVDC 系统直流故障特性研究[J]. 电工技术学报, 2017,32(10): 53-60.Chen Jikai, Sun Chuan, Li Guoqing, et al. Study on characteristics of DC fault in bipolar MMC-HVDC system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 53-60.
[6] 王晨清, 宋国兵, 汤海雁, 等. 选相及方向元件在风电接入系统中的适应性分析[J]. 电力系统自动化, 2016, 40(1): 89-95.Wang Chenqing, Song Guobing, Tang Haiyan, et al.Adaptability analysis of phase selectors and directional relays in power systems integrated with wind farms[J]. Automation of Electric Power System,2016, 40(1): 89-95.
[7] Zhou Yuebin, Jiang Daozhuo, Guo Jie, et al. Analysis and control of modular multilevel converters under unbalanced conditions[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 1986-1995.
[8] 刘子文, 苗世洪, 范志华, 等. 不平衡电网电压下柔性直流输电系统功率滑模补偿策略[J]. 电工技术学报, 2018, 33(14): 3296-3305.Liu Ziwen, Miao Shihong, Fan Zhihua, et al. Power sliding mode compensation strategy of VSC-HVDC under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3296-3305.
[9] Shi Xiaojie, Wang Zhiqiang, Liu Bo, et al.Characteristic investigation and control of a modular multilevel converter-based HVDC system under singleline-to-ground fault conditions[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 408-421.
[10] Zeng Rong, Xu Lie, Yao Liangzhong, et al. Analysis and control of modular multilevel converters under asymmetric arm impedance conditions[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1):71-81.
[11] Liang Yingyu, Liu Jianzheng, Zhang Tao, et al. Arm current control strategy for MMC-HVDC under unbalanced conditions[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 125-134.
[12] 苑宾, 许建中, 赵成勇, 等. 利用虚拟电阻提高接入弱交流电网的 MMC小信号稳定性控制方法[J].中国电机工程学报, 2015, 35(15): 3794-3802.Yuan Bin, Xu Jianzhong, Zhao Chengyong, et al. A virtual resistor based control strategy for enhancing the small-signal stability of MMC integrated in weak AC system[J]. Proceeding of the CSEE, 2015, 35(15):3794-3802.
[13] 刘炜, 郭春义, 赵成勇, 等. 一种适用于 MMCHVDC连接极弱受端交流电网的功率阻尼同步控制方法[J]. 中国电机工程学报, 2016, 36(17): 4647-4655.Liu Wei, Guo Chunyi, Zhao Chengyong, et al. Power damping synchronization control for MMC-HVDC connected to an extremely weak receiving AC grid[J].Proceeding of the CSEE, 2016, 36(17): 4647-4655.
[14] 丁久东, 田杰, 刘奎, 等. 柔性直流输电对交流系统负序方向元件影响分析[J]. 电力系统自动化,2017, 41(12): 113-117.Ding Jiudong, Tian Jie, Liu Kui, et al. Impact of VSCHVDC on negative sequence directional component in alternating current system[J]. Automation of Electric Power System, 2017, 41(12): 113-117.
[15] 陈实, 邰能灵, 范春菊, 等. 逆变型电源接入对选相元件的影响分析[J]. 电力系统自动化, 2017,41(12): 106-112, 187.Chen Shi, Tai Nengling, Fan Chunju, et al. Influence of inverter-interfaced generator on element of phase selectors[J]. Automation of Electric Power System,2017, 41(12): 106-112, 187.
[16] 张保会, 王进, 原博, 等. 风电接入对继电保护的影响(四)——风电场送出线路保护性能分析[J]. 电力自动化设备, 2013, 33(4): 1-5.Zhang Baohui, Wang Jin, Yuan Bo, et al. Impact of wind farm integration on relay protection(4):performance analysis for wind farm outgoing transmission line protection[J]. Electric Power Automation Equipment, 2013, 33(4): 1-5.
[17] 申洪明. 直流换相失败对交流侧保护的影响分析与对策研究[D]. 北京: 华北电力大学, 2016.
[18] 吴方劼, 马玉龙, 梅念, 等. 舟山多端柔性直流输电工程主接线方案设计[J]. 电网技术, 2014, 38(10):2651-2657.Wu Fangjie, Ma Yulong, Mei Nian, et al. Design of main connection scheme for Zhoushan flexible multiterminal HVDC transmission project[J]. Power System Technology, 2014, 38(10): 2651-2657.
[19] 赵新. 电励磁直驱风力发电机并网控制技术研究[D]. 北京: 北京交通大学, 2014.
[20] 黄涛, 陆于平, 凌启程, 等. 适应于双馈风电场的改进故障序分量选相方法[J]. 电力自动化设备,2016, 36(4): 123-128.Huang Tao, Lu Yuping, Ling Qicheng, et al. Improved fault-sequence component phase selector applied to DFIG-based wind farm[J]. Electric Power Automation Equipment, 2016, 36(4): 123-128.