0 引言
智能电网时代，随着柔性交流输电系统（Flexible AC Transmission Systems, FACTS）和多端直流输电工程（Multi-Terminal Direct Current, MTDC）投运，输电线路的传输功率将大幅度提高，但同时电网故障后引发的潮流转移也更严重。由故障引起的交流线路跳闸或直流闭锁，可能使其他线路过载，甚至引发联锁故障。因此，故障后及时实施合理的安全校正（Security Correction, SC）措施以尽快消除潮流越限，对于保障系统的安全运行具有重要意义。
制定安全校正方案通常采用的调整手段是调整发电机功率和切负荷，但两者效果有限，因此有必要寻求其他可以快速响应的手段，减少切负荷量并尽快达到预期的调整效果。研究表明:①多端直流可以同时独立控制有功和无功功率，快速改变潮流分布[1-2]；②FACTS设备可以增加约 50%的电网传输容量，对于潮流控制有非常显著的效果[3]；③传输线切换（Transmission Switching, TS）能够快速有效地调整故障后的潮流[4]。文献[5]基于美国电网的实际算例，仿真分析了超过150万种故障形式，发现在故障后如果允许开断一条线路，10%~33%的算例中的潮流越限现象可以被消除，56%~83%的算例中的潮流越限程度显著降低。鉴于 TS的有效性和快速性，在国外的一些实际电网中已将这一手段用于消除故障后潮流越限[6-7]。
安全校正策略的制定主要基于两类方法，灵敏度法[8-10]和优化规划法[11-13]。灵敏度法应用于拓扑结构固定的交流电网时，具有求解简单快速的优势，但是在变拓扑结构电网中的适应性有待研究。优化规划法具体可分为人工智能优化类方法[11-12]和数学规划类方法[13-16]。前者模型建立较易，但求解速度较慢，也较难寻求全局最优解。后者因其在求解速度和效果上的优势，近年来逐渐成为研究的热点，但是对于考虑 TS的安全校正问题，目前还存在两方面的问题值得进一步深入研究:
（1）准确性问题。包含了TS的安全校正问题是一个非线性的混合整数规划问题，目前该类数学问题的求解效率较低。为了降低计算复杂度，目前研究大多对其进行线性化处理。具体地，文献[6]基于直流潮流模型，构建了一种用于消除N-1-1故障越限的TS优化模型，验证了TS不仅可以消除故障后的越限，而且不会降低系统的可靠性。文献[14]在最优传输线切换问题中构建了两阶段的鲁棒优化模型，其中安全校正子问题也是基于直流潮流模型。但是电力系统本身是一个高度非线性的系统，若基于直流潮流模型分析校正方案可能不够准确。
（2）求解效率问题。TS问题中，支路的开断与否为0-1变量，但0-1变量的数量越多，其求解效率越低。为提高求解效率，应尽量缩减允许开断的线路数量。文献[5]提出了三种快速筛选线路的方法:①选择离故障元件最近的 n条线路；②选择离越限元件最近的n条线路；③基于大数据方法选线。文献[16]基于候选线路列表，逐条开断每一条线路，在固定拓扑下优化安全校正方案，最后筛选目标函数最优的结果。虽然在开断单条线路时效果较好，但是在需要同时开断多条线路时，其计算效率会显著降低。文献[17]针对每条越限支路分别选择对其潮流影响大的支路作为备选线路，但当越限支路数量较多时，可能导致备选线路过多，增加模型的求解难度。
基于上述分析，为了快速得到准确并且控制代价低的安全校正方案，本文提出了一种基于混合整数二阶锥规划（Mixed Integer Second Order Cone Programming, MISOCP），考虑了多种快速控制手段的电网综合安全校正策略。首先，为了减少切负荷量，提高安全校正方案实施的快速性，采取三种快速响应的潮流调整手段:可控串联补偿装置（Thyristor Controlled Series Capacitor, TCSC）补偿度优化、多端直流功率调制、传输线切换。然后，为了能够快速求解并获得准确的安全校正方案，基于混合整数二阶锥规划构建包含这三种快速控制手段的交流潮流模型，并在此基础上建立相应的综合安全校正优化模型。进一步，针对现阶段混合整数规划数学模型求解效率较低的问题，提出支路开断综合影响指标，并从筛选待开断支路和引导目标函数求解方向两个切入点提出了启发式双重加速求解策略。最后，基于改造的IEEE 57节点算例验证了所提基于二阶锥、综合考虑多种快速控制手段的安全校正策略及启发式双重加速求解策略的有效性和优越性。
1 基于二阶锥的含 TCSC、MTDC和 TS的可变拓扑电网的潮流模型
二阶锥规划（Second Order Cone Programming,SOCP）是一种能适应电网交流潮流模型且具有很高求解效率的数学规划方法，近年来其在电网潮流优化相关问题中得到较多关注，并且二阶锥松弛的有效性和准确性也得到验证[18-21]。
考虑TS之后，电网拓扑结构可变，线路的通断状态成为变量，记作Hij。当Hij=1时表示线路ij连通，当Hij=0时表示线路ij开断。区别于固定拓扑结构的电网潮流模型，将线路通断状态作为变量后，常规的二阶锥潮流模型不再适用，因为此时线路连通和开断应分别对应两套不同的潮流约束条件。而若要进行潮流优化，需将上述约束条件改写为可以同时兼容线路连通或者开断的统一形式。
因此，虽然已经有关于固定拓扑结构下常规电网二阶锥潮流模型的研究，但是如何在拓扑结构为变量的情况下，将含TCSC和MTDC电网的交流潮流模型转换为二阶锥形式，是本文研究的创新和难点之一。
在常规调整手段的基础上，针对采取 TCSC、MTDC和 TS这三种快速调控手段的需求，本章基于混合整数二阶锥规划构建了含 TCSC、MTDC且拓扑结构可变的电网潮流模型。
1.1 TCSC的二阶锥潮流模型
本文基于如图1所示的等效注入功率模型，研究TCSC二阶锥潮流模型以分析TCSC对于潮流的影响。该模型将线路潮流分为两部分，第一部分Sij只和原线路参数相关，而TCSC对线路潮流的影响全部被分离到第二部分STCi,ij上。
图1 TCSC等效注入功率模型
Fig.1 TCSC power injection model
图1 中，rij和xij分别为无TCSC时线路的电阻和电抗；Sij和Sji分别为无TCSC时线路ij两端的功率；Sijreal和 Sjireal分别为 TCSC接入后 ij两端的实际功率；STCi,ij和STCj,ij分别为TCSC接入后，从节点i和j注入线路ij的等效功率。
若要求出 TCSC的等效注入功率 STCi,ij，首先需要求出TCSC接入引起的线路参数变化。定义线路 ij上的 TCSC的补偿度为 kc,ij，通常
有
式中，xL,ij为 TCSC接入后线路 ij的电抗。一般输电线路上可忽略线路电阻rij，易知TCSC接入引起的线路电导和电纳的变化量Δgij和Δbij为
定义八个辅助变量为
式中，θij为线路ij的电压相位差
是TCSC的调节范围，kc,ij取最大/小值时，分别对应KTCij的最小/大值。
式中，在变量上方和下方加横线分别表示变量的上限和下限。观察发现，定义的八个变量符合如下关系:
因此，松弛式（6），可以得到二阶锥形式的约束
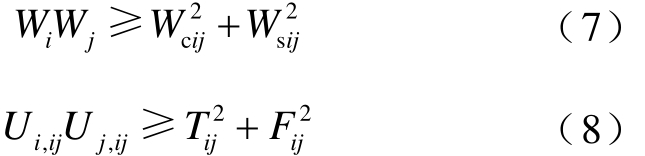
进而，线性化的TCSC注入功率为
为了在不影响其余潮流模型的前提下使 TCSC模型适应线路开断，需要约束所定义的四个辅助变量 Tij、Fij、Ui,ij和 Uj,ij，使线路开断时 TCSC的注入功率为0。观察式（4）知，四个辅助变量都符合
式中，X代表四个辅助变量；Y代表其在式（4）中对应的变量。需要指出，Y中的 Wi和 Wj需要分别被 W r i,ij和 W r j,ij替换。W r i,ij、W r j,ij是为了适应 TS而定义的新变量，在1.3节中将详细说明，这里不再展开。
为了使得这四个辅助变量在Hij=0时为0，在Hij=1时满足式（4），构建约束式（11）。需要指出，约束式（11）生成的变量X的上、下限范围并不是固定值，会随着变量Y和变量KTCij的变化而变化。
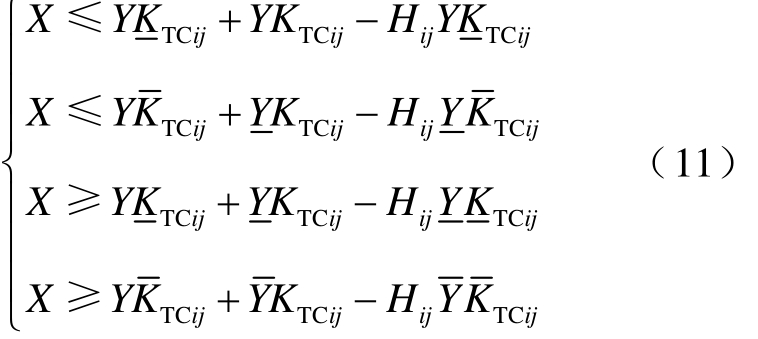
在所提出的基于二阶锥的TCSC潮流模型中，KTCij作为TCSC的控制变量参与安全校正优化，最后反解出kc,ij即为线路ij上的TCSC的补偿度。
1.2 MTDC的二阶锥潮流模型
构建MTDC的等效潮流模型时，可将每个换流器建模为一台虚拟的发电机，并且将换流器和公共连接点（Point of Common Connection, PCC）之间的耦合变压器和相电抗器等效为一条交流线路。ACDC网络的的等效潮流模型如图2所示[22]。
图2 AC-DC网络的等效潮流模型
Fig.2 Power flow model of AC-DC network
其基于二阶锥的潮流模型为
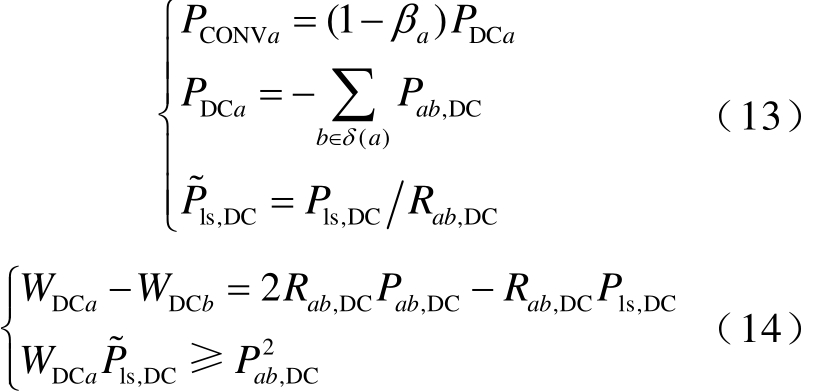
式中，PCONVa为从直流换流器a流入PCC的功率；PDCa为从直流网络流入换流器a的功率；βa为换流器a的损耗系数；Pab,DC为直流网络中从节点a流向节点b的功率；δ(a) 为直流网络中和节点a相邻的节点b的集合；Pls,DC为直流线路ab的功率损耗；WDCa为节点a的电压二次方；Rab,DC为直流线路ab的电阻。
其安全运行的上下限约束为
1.3 适应TS的变拓扑电网的二阶锥潮流模型
本节在含TCSC和MTDC的电网中进一步构建能够适应拓扑结构改变的基于二阶锥的潮流模型。
1.3.1 改进支路功率模型
在常规的节点注入功率模型中，为了计算方便，线路两端对地支路的电纳通常是归算至节点上，即这部分功率通常未计算为线路功率。但实际上对地电纳是由于线路的电容效应引起的，故对地支路的功率应该包含在线路功率内。所以在考虑TS的问题中，线路的对地支路应该作为线路的一部分，如图 3所示。
图3 考虑TS的支路功率模型
Fig.3 Branch flow model when considering TS
因此，支路功率的计算公式为
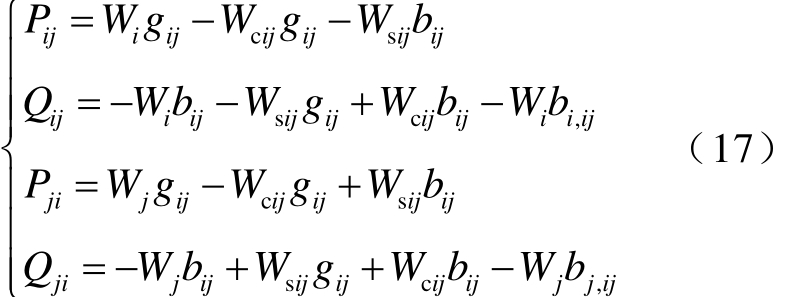
式中，Pij、Qij分别为从节点i流向节点j的有功、无功功率；bi,ij、bj,ij分别为线路ij的i侧、j侧的等效对地电纳。
在线路开断后Hij=0时，线路两端的有功和无功功率都应该为0。因此，应增加约束
为了在不影响其余潮流模型的前提下适应线路开断，需要约束式（17）中的四个辅助变量Wi、Wj、Wcij和 Wsij，使线路开断时它们都为 0。其中，Wcij、Wsij是只与本条线路相关的变量，所以可以通过式（20）约束它们在Hij=0时为0，而不影响其余的约束条件。
但是线路两端的电压二次方Wi、Wj是不可能为0的。因此，对线路ij的两端分别定义虚拟的电压二次方
和 
以分别代替Wi和 Wj。当线路连通Hij=1时，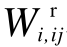
和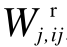 
应该和真实的电压二次方 Wi、Wj相等。当线路开断Hij=0时，
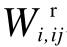和 
应该都为0。因此有
将式（17）中的Wi、Wj用W r i,ij、W r j,ij替换，可得
1.3.2 角度恢复模型
在环网中，必须对每个节点的电压相角θ进行约束，否则无法还原相角，模型失效。根据式（17）可得
由于在输电网中，θij通常非常小，可以假设sinθij≈θij=θi- θj，因此环网中的相位公式可以写为
式中，
、
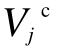分别为节点i、j电压的典型值，即1（pu）；θi、θj分别为节点 i、j的电压相角。
线路ij开断后，线路两端的相位差θij不再受到约束，可以不满足式（24）。因此，对线路ij两端定义一个虚拟相位差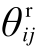
。当 Hij=1时，
和真实的相位差相等；当Hij=0时，θ r ij可以为任意值。故式（24）可被等效替换为
1.3.3 节点功率平衡公式
式中，PGi、QGi分别为节点 i的发电有功、无功功率；PLDi、QLDi分别为节点i的负荷有功、无功功率；δ(i)为与节点i相邻的节点的集合；η(i)为以节点i为TCSC支路的一端的另一端节点的集合。
2 考虑TCSC、MTDC和TS的SC模型
在第 1节所推导的基于二阶锥的含 TCSC、MTDC和TS电网的潮流模型的基础上，本节进一步构建了考虑调整TCSC、MTDC和TS的基于混合整数二阶锥的安全校正优化模型。
2.1 决策变量
决策变量指的是最终得到的安全校正方案中具体的调整措施，见表1。需要指出的是，由于负荷的功率实际上不能连续调节，故在所提出的模型中用0-1变量表示负荷的切除与否。
表1 安全校正模型的决策变量
Tab.1 Decision variables of security correction model
决策变量 变量类型 变量符号发电机有功、无功功率PGi、QGi TCSC补偿度 KTCij (kc,ij)MTDC换流器有功、无功功率 PCONVa、QCONVa负荷切除与否 0-1二元型连续型Ldi-k支路开断与否 Hij
2.2 目标函数
安全校正模型的首要目标是尽可能保有更多负荷。若存在切负荷量相同的多套方案，应选取尽量少调发电机出力的方案。假设每个负荷节点上接有nd个负荷，用PLDi-k和QLDi-k表示节点i上所接的第k个负荷的有功和无功功率。节点i上负荷k的切除与否用Ldi-k来表示，1表示不切除，0表示切除。那么，对于每个负荷节点i，其有功和无功功率为
因此可构造目标函数
式中，PGi,0为故障前i的发电有功功率；M为一个较大的惩罚系数，可令其为1 000。
2.3 安全约束条件
除了已列出的支路潮流约束式（18）、式（19）和电压安全约束式（21）等外，还需要考虑一些安全约束条件。
1）发电机调整数量约束
为了避免最后得到的安全校正方案操作过于复杂，比如所有发电机都参与调整但是每台发电机的调整量又非常小[23]，应约束参与调整的发电机的总数。
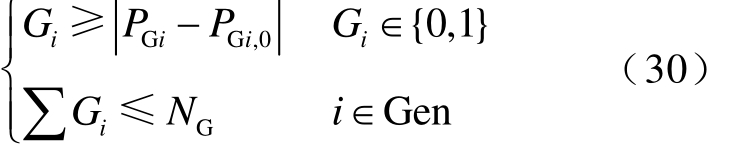
式中，Gi为 1表示调整发电机 i，Gi为 0表示不调整；NG为最大允许调整的发电机数量。
2）允许开断的线路数量约束
式中，NL为最大允许开断的线路数量。
3）发电机功率约束
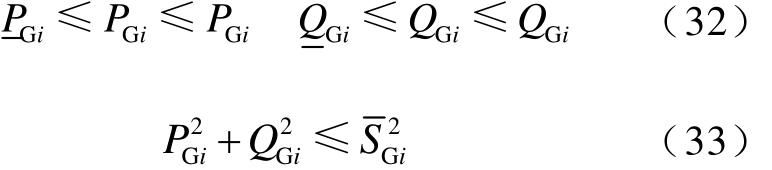
4）节点电压约束
2.4 完整的混合整数二阶锥安全校正模型
综上，可以写出考虑了调整TCSC、MTDC和TS的基于混合整数二阶锥的电网安全校正优化模型。
约束条件:①线性等式约束:式（9）、式（13）、式（22）、式（25）、式（27）和式（28）；②线性不等式约束:式（5）、式（11）、式（15）、式（18）、式（20）、式（21）、式（26）、式（30）、式（31）、式（32）和式（34）；③二阶锥约束:式（7）、式（8）、式（14）、式（16）、式（19）和式（33）。
2.5 模型求解方法
所提出的考虑了调整TCSC、MTDC和TS的可变拓扑结构电网的安全校正优化模型是一个标准的混合整数二阶锥规划数学模型，因此可以通过成熟的商用软件比如 CPLEX、GUROBI、MOSEK等求解。本文采取在Matlab 2014a中编程，并通过CVX调用GUROBI求解。
3 启发式双重加速求解策略
由于现阶段混合整数规划类问题的求解效率较低，为了快速求解第2节中提出的安全校正模型，本节提出了一种启发式双重加速求解策略，从两方面加速求解过程:①提出了基于支路开断综合影响指标的启发式选线策略，其加速原理是缩减0-1二元型优化变量的数量，降低搜索空间的维度；②将所提指标引入目标函数，通过引导求解的方向，加速收敛过程。
3.1 基于支路开断综合影响指标的启发式选线
由于包含了 TS的混合整数规划问题的求解效率会随着0-1二元变量数量的增加而降低，因此如果能够在优化之前就尽可能地减少参与优化的 0-1变量的数量，将有效缩短计算时间。
为在保证效果的前提下合理缩减参与优化的 TS变量的数量，应选出开断后能有效降低越限支路的潮流的线路。针对故障后多条线路出现潮流越限的情况，则应选择开断后能够从总体上缓解越限的线路。
为避免反复的潮流计算，基于支路开断分布因子（Line Outage Distribution Factors, LODF）[24]提出了线路 l开断对所有越限支路潮流的综合影响指标IFl。该指标能够从总体上反映线路 l开断之后对所有越限支路k的潮流的综合影响效果。
式中，OL为越限支路的集合；Pl为线路l的功率；Pk为潮流越限的线路k的功率；Dk,l 支路 l开断对支路k的LODF指标。
如果在计算LODF时，以潮流的实际方向为正方向，可得如下结论:
1）当Dk,l＜0时，表示开断支路l后，支路k的潮流会降低；反之，则表示支路k的潮流会增加。
2）当支路 l的功率改变相同的量值时，Dk,l的绝对值越大，支路k的潮流受到的影响越大。
3）IFl＜0，表示开断支路 l对所有越限支路的潮流的综合影响效果是缓解越限；反之则反。
4）IFl的绝对值越大，则表示开断支路l对所有越限支路的潮流的综合影响效果越大。
因此，应当选取IFl指标最小（小于0且绝对值最大）的几条支路，这些支路开断后能够最大限度地从整体上缓解越限。以这些支路作为待开断的支路参与优化，即可大幅度缩减 0-1变量的数量，降低搜索维度，提高计算效率。
3.2 诱导目标函数的加速求解策略
由于通过采取合适的 TS动作，能够达到缓解越限的效果，因此 TS可以在一定程度上降低其他调控手段的调整量，比如可以减少切负荷量和发电机的调整量。因此，通过选择合适的TS支路开断，可以减小目标函数的值。而根据 3.1节的分析可以知道，综合影响指标 IFl越小的支路，其缓解越限的效果越明显，更有利于实现上述目标。
因此综合考虑之后，将所提出的支路开断综合影响指标引入目标函数中，以在求解过程中引导求解方向，加速收敛。据此，提出了诱导目标函数加速求解策略。修正后的目标函数为
式中， lH表示线路l的开断， lH=1表示连通， lH=0表示开断；SL为3.1节中选出的可开断支路的集合；Cv为IFl指标的放大/缩小倍数。因为式（37）中附加的目标函数不应该影响式（35）的结果，所以通过Cv对IFl指标进行缩放，使目标函数的附加项在合理范围内。
式中，IFl,n是将 IFl指标从小到大排序之后，排第n位的指标的数值；Cd为与原目标函数的最大的差值。
对于最小化问题，相对IFl指标越大的支路，IFl指标越小的支路会受到更大的让线路开断（Hl=0）的“吸引力”。因此，所提的诱导目标函数加速求解策略能够优先“吸引”所有IFl指标较小（具有更好的缓解越限的效果）的支路使其开断，以减小目标函数。相对于所有支路开断都是等权重的情况，该方法在求解过程中目的更明确，方向性更强。
由于对每条支路的开断与否都赋予了对应的权重，所以在求解的过程中，该诱导目标函数可以正确引导模型的求解方向、加速收敛过程。因此，以式（37）为目标函数的安全校正模型相对于以式（35）为目标函数的模型更容易求解，因而也具有更高的求解效率。
4 算例验证
基于改进的IEEE 57节点算例验证所提出的考虑传输线切换的电网安全校正策略及快速求解方法的有效性。
4.1 算例简介与参数设置
在图4所示的标准IEEE 57节点算例[25]基础上，增加了多端直流输电系统和 TCSC装置，以验证这些快速控制手段的控制效果。三端直流系统的三个电压源型换流器VSC1、VSC2和VSC3分别接在交流节点12、28和18上，每两个换流器之间由一条直流线路连接，共有3条直流线路。线路1（节点9-节点 13）和线路 2（节点 9-节点 11）上安装了 TCSC装置。改造后的IEEE 57节点算例共有57个交流节点、80条交流线路、7台发电机、42个负荷节点、3个电压源型换流器、3条直流线路、2个 TCSC装置。
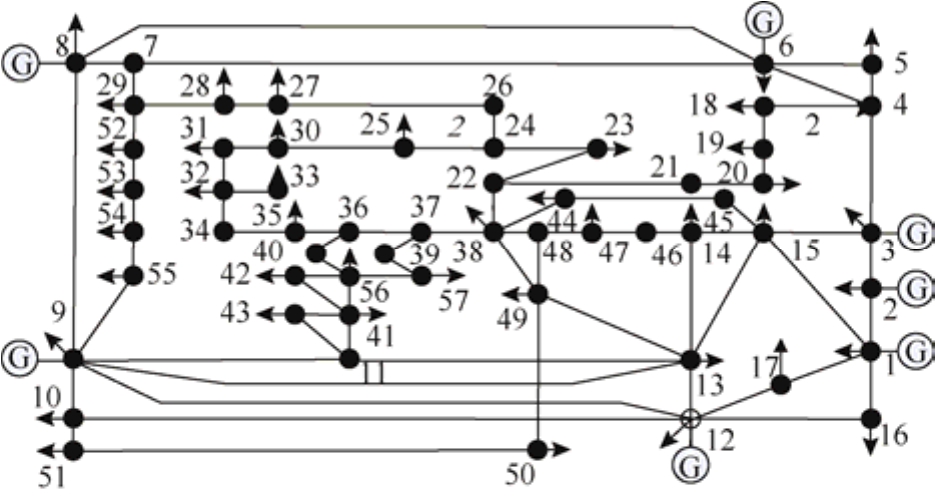
图4 标准IEEE 57节点接线图
Fig.4 Standard IEEE 57 bus system
对改造后的算例设置必要的安全约束，需指出，本节仅以一种约束为例进行算例验证，文中所提方法可以适应于不同的安全约束，实际应用时应根据系统情况调整。假设交流线路的潮流上限为初始潮流的1.5倍，如果线路初始潮流过小，则假设潮流上限为0.3（pu）。3个VSC的最大容量均为1.0（pu），2个TCSC补偿度范围均为[-0.4,0]。安全校正方案中最多允许调整 3台发电机。考虑到发电机的调节需时间，假设在安全校正所允许的调节时间内，每台发电机的出力最高可为初始值的1.3倍，最低为0.7倍。每个负荷节点上都接有2个负荷，分别记为i-1和i-2，其功率的比值为1:2。i表示负荷所在的节点号。每个故障下仅允许切换一条线路。上述所有条件都可改动。
所有测试结果均在Windows 7 64位操作系统上获得，CPU处理器为Intel(R)Core(TM)i7-4790 3.60GHz，内存为8GB。
4.2 所提模型的有效性和准确性验证
基于改造的IEEE 57节点算例的所有N-1和部分N-2故障，验证所提模型的准确性。以线路15（节点 13-节点15）和线路18（节点1-节点 17）故障跳闸的N-2故障为例，进行具体的分析。
在 3.1节中提出了基于线路开断对所有越限支路的潮流综合影响指标筛选待开断线路的方法。在57节点算例中，对每个故障选取排序最靠前的 10条线路作为待开断线路。对于线路15+18的断线故障，故障后共有7条线路出现潮流越限，总越限量为1.364(pu)。基于所提方法筛选出的待开断线路为线路 28、14、27、13、19、66、16、23、65和线路4，即优化过程中仅这10条线路允许开断，其余线路均保持连通。
为了同时验证三种快速控制手段的控制效果，设置了四组场景，每组场景的控制手段均不同:①场景1:只调发电机功率和切负荷；②场景2:比场景1增加TCSC和MTDC调整；③场景3:比场景1增加TS；④场景4:包含所有的控制手段。
四组场景下得到的安全校正方案见表 2。表中展示了发电机、换流器有功功率和TCSC补偿度的调整方案，以及被切除的负荷和进行TS的线路。
表2 四组场景下的安全校正方案
Tab.2 Security correction schemes under 4 scenarios
变量 初始量 场景1 场景2 场景3 场景4 Gen1(pu) 3.586 2.612 2.586 2.651 2.799 Gen3(pu) 1 0.7 0.994 — —Gen6(pu) 0.7 — — 0.91 0.849 Gen7(pu) 2.1 2.73 2.73 2.73 2.73 VSC1(pu) 0.5 — 0.918 — 0.660 VSC2(pu) -0.23 — -0.420 — -0.094 VSC3(pu) -0.28 — -0.531 — -0.578 TCSC1 0 — -0.373 — -0.292 TCSC2 0 — -0.386 — -0.353被切负荷 13-1,13-2,17-1,17-2 17-2,30-2,31-1,32-1 13-1,43-2 —被开断线路 — — 66 66发电有功调整量(pu) 1.904 1.636 1.775 1.567负荷有功切除量(pu) 0.6 0.329 0.087 0目标函数 601.904 330.336 88.775 1.567优化时间/s 0.74 0.87 1.29 1.08
为了校验这四组安全校正措施实施后是否能够有效消除越限，采用 Matpower软件的牛顿拉夫逊法潮流计算方法进行潮流校验。基于所提出的MISOCP模型（表 3中记为 SOCP）和基于牛顿拉夫逊法（记为NL）得到的实施安全校正措施后的潮流结果见表3。限于篇幅，只列出了 TCSC支路和越限支路上流过的最大有功功率的结果。经过校验发现实施安全校正措施之后，所有的越限都被消除。
表3 四组场景下的潮流校验结果
Tab.3 Power flow results under 4 scenarios
（标幺值）线路 潮流上限场景1 场景2 场景3 场景4 SOCP NL SOCP NL SOCP NL SOCP NL 1 0.3 0.159 5 0.159 7 0.246 5 0.238 4 0.193 5 0.196 2 0.225 8 0.222 5 2 0.37 0.267 0 0.266 5 0.268 8 0.274 1 0.302 2 0.304 2 0.337 5 0.326 3 3 0.3 0.169 6 0.160 2 0.166 4 0.160 0 0.103 2 0.096 1 0.177 5 0.177 1 13 0.44 0.183 5 0.180 4 0.081 1 0.079 0 0.436 1 0.429 6 0.428 9 0.410 0 14 0.3 0.300 0 0.285 4 0.300 0 0.293 5 0.300 0 0.287 6 0.300 0 0.296 3 17 1.18 0.759 0 0.758 8 0.736 1 0.740 2 0.843 9 0.845 7 0.857 7 0.861 1 26 0.49 0.303 4 0.303 2 0.282 1 0.285 9 0.382 8 0.384 6 0.396 0 0.399 0 28 1.11 0.933 9 0.918 0 0.918 9 0.925 1 1.039 6 1.024 2 1.031 7 1.026 2 57 0.39 0.284 8 0.296 0 0.294 9 0.307 1 0.368 9 0.373 6 0.370 1 0.377 1
分析表2和表3中的数据，可以得到如下结论:
（1）所提出的基于二阶锥的含TCSC、MTDC和TS的潮流模型是准确的。通过对比 MISOCP和牛顿拉夫逊法的潮流结果，发现每组场景下两者都非常接近。并且大量算例计算表明，两种算法得到的每条支路的潮流误差均小于 0.02(pu)，其平均误差约为0.003 4(pu)。
（2）所提出的安全校正优化模型是有效的。分析表3中基于牛顿拉夫逊法校验的4组场景下实施安全校正方案后的潮流结果，发现所有支路的潮流都已降至安全范围内，验证了所提出模型的有效性。
（3）TCSC、MTDC和TS参与调整都能显著减少切负荷量和发电机调整量，甚至可以不切负荷。在完全不考虑这三种手段的场景 1中，切负荷总量为0.6(pu)。在考虑直流和TCSC的场景2中，切负荷总量降至0.329(pu)，是场景1的54.7%。在考虑TS的场景3中，仅切除了场景1的14.5%的负荷。而在三种手段全部考虑的场景4中，已经无需再切负荷。这说明传输线切换对于消除潮流越限具有非常良好的调控效果。大量算例计算表明，对于一些越限不严重的故障，仅切换一条线路就可以不用再切负荷。
（4）所提出的模型可以被快速求解。在不考虑传输线切换的场景1和场景2，基于GUROBI求解该混合整数二阶锥模型，仅需0.8s左右。对于考虑了传输线切换的场景3和场景4，采用了所提出的启发式双重加速求解策略后，优化时间可以缩短至1.2s左右，较为接近场景1和场景2。而在文献[11]中，基于人工智能优化算法中速度较快的模拟植物生长法，计算IEEE 30节点算例的安全校正措施至少也需要68.4 s。对比可以看到，本文方法所处理的算例规模更大、采用的控制手段更多，但优化耗时仅为文献[11]结果的1.58%。可见本文方法在计算速度上具有显著的优势。需要指出，在本文模型中，切负荷是作为 0-1变量考虑，如果将其近似处理为连续型变量，求解时间还将大幅缩短。
从上述分析可以看出，本文所提基于二阶锥、考虑TCSC、MTDC和TS三种快速调整手段的安全校正策略可以快速获得准确合理的安全校正方案，并且能够大幅度降低切负荷量，甚至不切除负荷。同时也能减少发电机的调整量，使得校正方案尽快生效。相比基于人工智能优化算法的安全校正策略，本文方法在计算效率上有巨大优势。
4.3 三种快速控制手段的优越性验证
为了进一步验证本文采取的三种快速控制手段在减小控制代价方面的优越性，基于IEEE 57节点算例的所有N-1和部分 N-2故障校验了三种快速控制手段的优越性。图5给出了其中30种会导致潮流越限的故障形式下，场景 4（采取三种快速控制手段）和场景1的安全校正方案的目标函数对比结果。
图5 快速控制手段的优越性验证
Fig.5 Verification of superiority of fast control measures
从图5中可以看出，三种快速控制手段能够有效减少控制代价，甚至在部分故障下，无需调整发电机和切除负荷就能消除越限。经牛顿拉夫逊法潮流校验，所有故障下，所得安全校正方案都能有效消除越限。
4.4 启发式选线方法的有效性验证
为了验证 3.1节中基于支路开断综合影响指标的启发式选线策略的有效性，从两方面展开验证:
（1）所提选线策略是否能够有效选出最优切换线路。如果能够选出最优切换线路，则说明策略有效。
（2）若未能选到最优切换线路，基于式（35）计算的目标函数会有多大误差。若误差较小，也认为策略有效。
具体的操作步骤如下:
（1）假设所有的线路都可以开断，优化得到最优的 TS方案，记目标函数为 f1，最优开断线路为 A。
（2）计算所有线路的支路开断综合影响指标（3.1节）并从小到大排序，记录最优线路A的排序位数。
（3）筛选排序前10位的线路构成可开断支路的集合SL进行安全校正优化，记目标函数为f2。
（4）计算两者的目标函数误差率
基于4.3节中选取的30组故障校验启发式选线方法的有效性，图6展示了校验的结果。
校验结果表明:
（1）如果最优开断线路A能够被筛选到可开断支路的集合SL中，则最终的结果一定是开断线路A。
图6 最优线路排序号和目标函数误差率
Fig.6 Rank number of the selected lines and the errors between objective functions
（2）绝大多数故障形式下该选线方法能够有效选取最优线路，最优线路A的排序号都在10以内。
（3）对于最优线路未被选为可开断支路的情况，即在优化时不允许开断A线，其目标函数误差率也较小，在10%左右，并不会显著影响TS的调整效果。
由于所提指标的计算基于灵敏度，其本质是一种线性化的方法，因此无法保证在任何情况下都一定能选到最优线路，但是在绝大多数情况下都可有效选出最优开断支路。即使在个别情况下没有选到，大量测试结果表明，相对于不考虑 TS的安全校正方案，开断非最优线路的 TS方案在调整效果上也具有显著优势，因此可以认为该选线方法是有效的。
还需指出，若在选线时多选一些线路，可提高最优开断支路被选择的概率，但相应地，模型求解速度会增加。比如筛选图6中排序前15位的线路构成可开断支路的集合，则最优开断支路 100%被选择。
4.5 启发式双重加速求解策略的效果验证
为了验证所提出的启发式双重加速求解策略的加速效果，基于以下三种情景进行了计算:A不采取任何加速手段；B只采取3.1节的选线加速；C同时采取 3.1节的选线加速和 3.2节的诱导目标函数加速。
分别将情景B和C的计算时间和情景A对比，以验证加速策略的效果。同时对比情景C与B的目标函数，以验证采取诱导目标函数加速策略后是否会影响优化结果。图 7展示了 4.3节的 30组故障下，情景B和C相对情景A节约时间的百分比。
由图7可知:
（1）分析实线可知，所提出的启发式双重加速求解策略最高可节约 97.7%的时间，平均可节约92.3%的时间，极大地提高了求解效率。
（2）分析虚线可知，启发式选线对于加速求解起到了主要的作用。选线最高可节约 97%的时间，平均可节约87.7%的时间。
图7 加速求解方法节约时间
Fig.7 The time saved by accelerating method
（3）分析实线相对于虚线所节约的时间可知，所提的诱导目标函数加速策略也有效提高了求解效率。其最高节约了57.5%的时间，平均节约了31.7%的时间。
需要特别说明，情景C和B的优化结果是完全一致的，即诱导目标函数加速策略并不会影响最终的切负荷量和发电机调整量，即并不会破坏解的最优性。
从验证结果来看，第3节所提出的加速求解方法大幅度地减少了求解时间，验证了本文所提出的启发式双重加速求解策略能够在不影响解的最优性的前提下显著提高求解速度。
5 结论
本文基于混合整数二阶锥规划提出了一种考虑了调整TCSC、MTDC和TS的安全校正策略，可以快速得到切负荷量少且准确（保守性小）的校正方案。为了进一步提高模型的求解效率，还从缩减二元变量数量和引导求解方向两方面缩短了安全校正方案生成时间。基于改造的IEEE 57节点算例对本文方法进行验证，得到如下结论:
1）所提基于二阶锥、含TCSC、MTDC的可变拓扑电网的有功潮流模型准确。所构建的基于二阶锥、考虑调整TCSC、MTDC和TS的综合安全校正策略能快速得到可有效消除电网中所有支路越限的安全校正方案。
2）TCSC参数优化、MTDC功率调整，尤其是TS，都可以显著减少切负荷量，甚至无需切除负荷，同时也可以减少发电机调整量，使得校正方案更快生效。
3）所提基于支路开断综合影响指标的启发式选线策略是有效的。在此基础上进一步提出的启发式双重加速求解策略能在不影响安全校正方案性能的前提下显著提高求解速度。
本文所提方法能够快速得到准确的安全校正方案，对于在线制定安全校正方案具有重要的参考价值。后续还将深入探讨更合理的线路筛选方法以及更快速的求解方法，为在线应用提供支撑，并进一步基于实际系统算例开展本文方法的工程应用研究。
[1] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12.Xu Dianguo, Liu Yuchao, Wu Jian. Review on control strategies of multi-terminal direct current transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 1-12.
[2] 吴杰, 王志新. 多端柔性直流输电系统的改进下垂控制策略[J]. 电工技术学报, 2017, 32(20): 241-250.Wu Jie, Wang Zhixin. Improved droop control strategy for multi-terminal voltage source converter-HVDC[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 241-250.
[3] Sahraei-Ardakani M, Hedman K W. Day-ahead corrective adjustment of FACTS reactance: a linear programming approach[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2867-2875.
[4] 李明扬, 方连航, 赵千川, 等. 用于电网安全校正的传输线切换策略研究综述[J]. 电网技术, 2017,41(8): 2506-2513.Li Mingyang, Fang Lianhang, Zhao Qianchuan, et al.Review on corrective transmission line switching[J].Power System Technology, 2017, 41(8): 2506-2513.
[5] Li Xingpeng, Balasubramanian P, Sahraei-Ardakani M, et al. Real-time contingency analysis with corrective transmission switching[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2604-2617.
[6] Abdi-Khorsand M, Sahraei-Ardakani M, Al-Abdullah Y M. Corrective transmission switching for N-1-1 contingency analysis[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1606-1615.
[7] Switching solutions, PJM, norristown, PA, USA [EB/OL]. https://www.pjm.com/markets-and-operations/etools/oasis/system-information/switching-solutions.aspx, 2018-10-08.
[8] 牟颖, 张保会, 薄志谦. 防止输电断面联锁过载的快速控制算法[J]. 电力系统自动化, 2017, 41(3): 39-45.Mou Ying, Zhang Baohui, Bo Zhiqian. Fast control algorithm for preventing cascading overload on transmission section[J]. Automation of Electric Power Systems, 2017, 41(3): 39-45.
[9] 任建文, 何培成, 何宸. 基于虚拟控制单元与启发式搜索的线路过载紧急控制策略[J]. 电力系统自动化, 2017, 41(3): 33-38.Ren Jianwen, He Peicheng, He Chen. Emergency control strategy against line overload based on virtual control units and heuristic search[J]. Automation of Electric Power Systems, 2017, 41(3): 33-38.
[10] 刘静文. 输电断面快速搜索及防联锁过载有功校正控制策略研究[D]. 秦皇岛: 燕山大学, 2016.
[11] 毕如玉, 林涛, 陈汝斯, 等. 交直流混合电力系统的安全校正策略[J]. 电工技术学报, 2016, 31(9): 50-57.Bi Ruyu, Lin Tao, Chen Rusi, et al. The security correction strategy in AC and DC hybrid power system[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 50-57.
[12] 任建文, 魏俊姣, 谷雨峰. 基于多目标粒子群优化算法的联锁跳闸预防控制[J]. 电力自动化设备,2016, 46(7): 53-59.Ren Jianwen, Wei Junjiao, Gu Yufeng. Preventive control based on multi-objective particle swarm optimization algorithm for cascading trips[J]. Electric Power Automation Equipment, 2016, 46(7): 53-59.
[13] Bi Ruyu, Lin Tao, Chen Rusi, et al. Alleviation of post-contingency overloads by SOCP based corrective control considering TCSC and MTDC[J]. IET Generation, Transmission & Distribution, 2018, 12(9):2155-2164.
[14] Ding Tao, Zhao Chaoyu. Robust optimal transmission switching with the consideration of corrective actions for N-k contingencies[J]. IET Generation, Transmission& Distribution, 2016, 10(13): 3288-3295.
[15] Dehghanian P, Wang Yaping, Gurrala G, et al.Flexible implementation of power system corrective topology control[J]. Electric Power Systems Research,2015, 128: 79-89.
[16] Balasubramanian P, Hedman K W. Real-time corrective switching in response to simultaneous contingencies[J]. Journal of Energy Engineering, 2015,141(1): B4014003.
[17] Lyon J D, Maslennikov S, Sahraei-Ardakani M, et al.Harnessing flexible transmission: corrective transmission switching for ISO-NE[J]. IEEE Power and Energy Technology Systems Journal, 2016, 3(3): 109-118.
[18] Kocuk B, Dey S S, Sun X A. Strong SOCP relaxations for the optimal power flow problem[J]. Operations Research, 2016, 64(6): 1177-1196.
[19] Farivar M, Low S H. Branch flow model: relaxations and convexification-part I[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564.
[20] 李静, 戴文战, 韦巍. 基于混合整数凸规划的含风力发电机组配电网无功补偿优化配置[J]. 电工技术学报, 2016, 31(3): 121-129.Li Jing, Dai Wenzhan, Wei Wei. A mixed integer convex programming for optimal reactive power compensation in distribution system with wind turbines[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 121-129.
[21] 张艺镨, 艾小猛, 方家琨, 等. 基于极限场景的两阶段含分布式电源的配网无功优化[J]. 电工技术学报, 2018, 33(2): 380-389.Zhang Yipu, Ai Xiaomeng, Fang Jiakun, et al. Twostage reactive power optimization for distribution network with distributed generation based on extreme scenarios[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 380-389.
[22] Baradar M, Hesamzadeh M R, Ghandhari M. Secondorder cone programming for optimal power flow in VSC-type AC-DC grids[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4282-4291.
[23] 顾雪平, 张尚, 王涛, 等. 安全域视角下的有功安全校正优化控制方法[J]. 电力系统自动化, 2017,41(18): 17-24.Gu Xueping, Zhang Shang, Wang Tao, et al.Optimization control strategy for active power correction from perspective of security region[J].Automation of Electric Power Systems, 2017, 41(18):17-24.
[24] 赵峰, 孙宏斌, 张伯明. 基于电气分区的输电断面及其自动发现[J]. 电力系统自动化, 2011, 35(5): 42-46.Zhao Feng, Sun Hongbin, Zhang Boming. Electrical zone division based automatic discovery of flowgates[J]. Automation of Electric Power Systems,2011, 35(5): 42-46.
[25] Power systems test case archive-57 bus power flow test case [EB/OL]. https://labs.ece.uw.edu/pstca/pf57/pg_tca57 bus.htm,2018-10-08.