0 引言
风力发电具有间歇性、随机性、可调度性低等不足，大规模风电并网会对电力系统特别是区域性互联电网的安全稳定产生新的威胁。文献[1-2]指出，互联电网复杂度的增加会加剧区间低频振荡，甚至会导致系统的解列，引发大面积电网故障。电力系统稳定器（Power System Stabilizer, PSS）是抑制低频振荡的主要措施之一，但仅以本地信号作为输入的PSS对于抑制区间振荡难以取得令人满意的效果。广域测量系统（Wide Area Measurement System,WAMS）和同步相量测量单元（Phasor Measurement Unit, PMU）的应用扩大了控制器输入信号的选取范围，为电力系统实现广域阻尼控制提供了可能，但同时也引入了时滞问题，文献[3-5]指出时滞的存在会削弱闭环控制的效果甚至出现恶化。因此有必要考虑时滞的影响。
时滞的处理方法有两大类。一是考虑时滞影响的鲁棒阻尼控制，使电力系统在可承受的时滞范围内维持稳定。文献[5]利用自由权矩阵方法推导了时滞相关稳定性判据，并结合状态观测理论设计了广域阻尼控制器。文献[6]基于网络控制系统（Networked Control System，NCS）理论设计考虑时滞的状态反馈控制器，对时滞系统进行阻尼控制。文献[7]给出了基于线性矩阵不等式（Linear Matrix Inequality，LMI）的Lyapunov稳定条件，并设计出具有一定时滞裕度的广域阻尼控制器。文献[8]将Lyapunov-Krasovskii泛函理论用于多时滞系统的控制，将镇定问题转换为LMI的可行性问题。文献[9-10]在广域时滞鲁棒控制中考虑了时滞容忍上限和系统阻尼比之间的优化问题。基于LMI的稳定判据是充分条件，具有一定的保守性和复杂性。另外应用于多机系统时，为了避免“维数灾”而采取的对被控对象的近似降阶会降低模型的准确度，从而影响系统的控制效果。二是对时滞环节进行直接补偿。文献[11]采用 Smith预测方法处理反馈控制中的时滞问题，引入与系统并联的滞后环节，从而使系统的等效传递函数中不包含时滞项。文献[12]利用统一Smith预估器消除时滞影响，并采用标准H∞混合灵敏度设计控制器。文献[13]将改进 Smith预估器引入电力系统广域控制，提高了系统的稳定性。时滞补偿法原理简单，计算方便，但是这种固定补偿时滞的方法，难以适用于不同时滞情况。
自抗扰控制[14]（Active Disturbance Rejection Control，ADRC）因其不依赖被控对象精确数学模型和对不确定因素估计补偿的优点而备受关注，已广泛应用于电机控制[15-17]和系统阻尼调节。文献[18]基于ADRC和非线性控制理论，提出一种抑制火电机组中低频振荡的本地控制方法。文献[19-20]分别设计用于光伏并网系统的 ADRC控制器和风电场STATCOM 附加阻尼控制器，改善了系统阻尼。针对时滞系统，韩京清基于自抗扰技术提出了无视时滞法、阶次提高法、输出预估法和输入预估法四种方法，但只适用于时滞较小的场合[14]。针对上述情况，本文提出将ADRC和Smith预估器相结合的广域电力系统附加阻尼控制器SP-ADRC，利用渐消记忆递推最小二乘法实现时滞的在线估计，以 Smith预估器降低时滞环节的影响，保留ADRC控制器对受控模型不敏感的优点。通过 SP-ADRC控制器调节风电场有功功率来改善系统阻尼。最后以含风电场的新英格兰10机39节点系统为例，验证所提策略的有效性。
1 自抗扰控制原理
1.1 自抗扰控制基本思想
自抗扰控制器将简单的积分器串联型系统作为反馈系统的标准型，而将异于标准型的其余未知部分视为总扰动，并将总扰动扩张为系统新的状态变量，利用扩张状态观测器和前馈补偿，对系统未知部分进行估计和补偿。因此，自抗扰控制不再依赖于被控对象精确的数学模型。以式（1）表示的n阶系统为例，说明动态补偿线性化的基本思想。
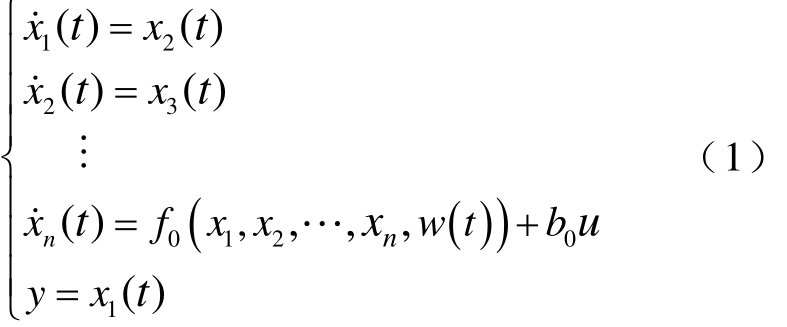
式中，x1, x2, …, xn为被控对象的状态变量；w(t)为系统模型中的不确定因素和外部扰动的总和；f0(x1, x2, …, xn, w(t))为状态变量函数；b0为控制量的反馈系数。
控制变量取
式中，u0由ADRC的状态误差反馈律计算所得。此时系统即转换为式（3）所示的线性积分器串联型系统。
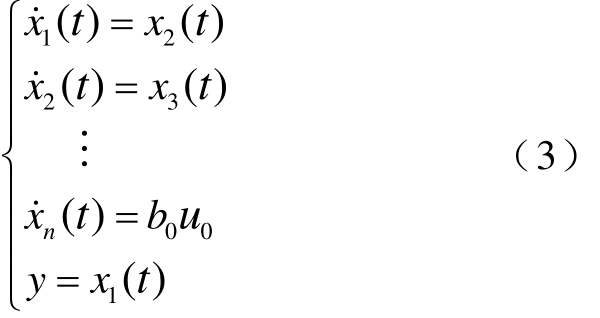
1.2 自抗扰控制器的构成
自抗扰控制器由非线性跟踪微分器（Tracking Differentiator, TD）、扩张状态观测器（Extended State Observer, ESO）、非线性误差反馈（Nonlinear State Error Feedback, NLSEF）和扰动估计补偿等构成。二阶ADRC结构如图1所示。
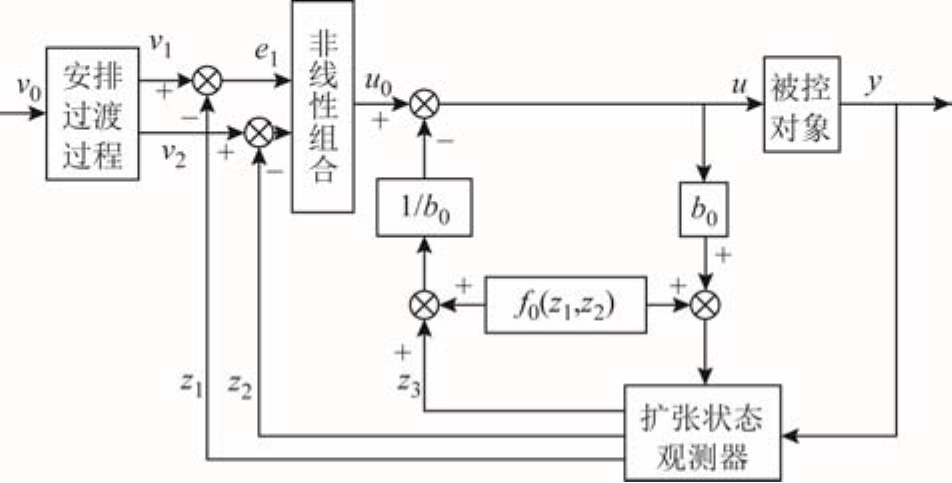
图1 自抗扰控制器的组成
Fig.1 Composition of ADRC
1.2.1 跟踪微分器
以给定的控制目标v0作为输入，安排过渡过程v1，得到其微分信号 v2，实现输出信号对系统输入快速无超调的跟踪，改善闭环系统的品质。
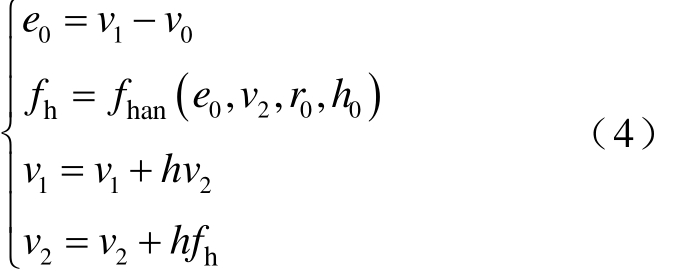
式中，r0为速度因子；h0为滤波因子；h为仿真步长；fhan(x1,x2,r0,h0)为最速控制综合函数，其算法表达式为
式中，d、d0为fhan函数线性段长度；y、a、a0为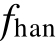
函数的内部变量；sign(x)为符号函数。
1.2.2 扩张状态观测器
ESO是自抗扰控制器的核心部分，不仅可以利用系统的输入y和输出u来实时跟踪估计系统的状态变量x1、x2，记为z1、z2，还可将能反映在输出信号中的未知部分 w(t)扩张成新的状态变量并加以估计，记为z3。
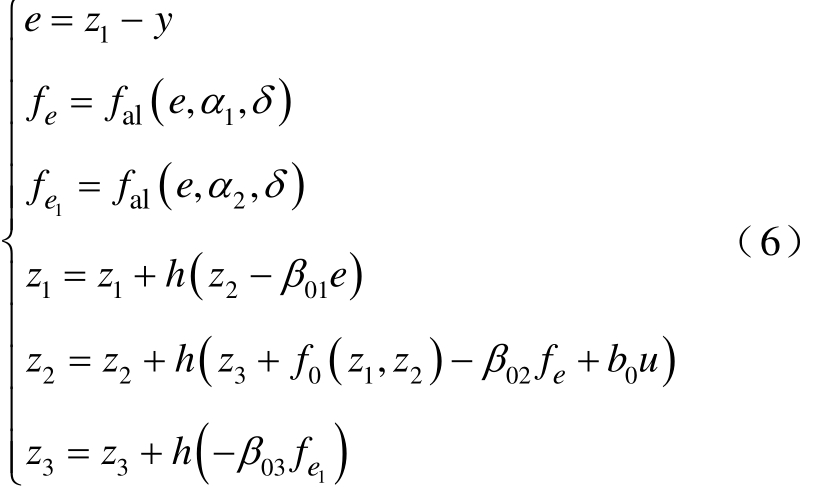
式中，β01、β02、β03为一组增益系数；α1、α2为幂函数指数，一般取为0＜α≤1；δ为线性段区间的长度；fal(e,α,δ)为原点附近具有线性段的连续的幂次函数，防止在数值仿真时出现高频振颤，表达式为
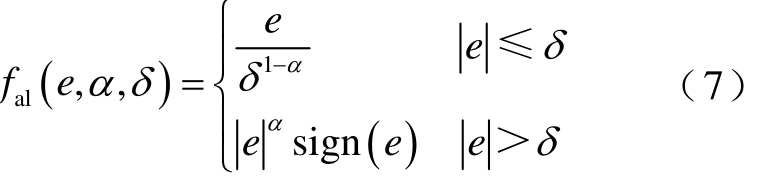
1.2.3 非线性误差反馈
根据状态误差信息e1、e2求取作用于简单积分器串联型系统的控制量u0，合适的误差反馈律有利于改善控制器的效率。
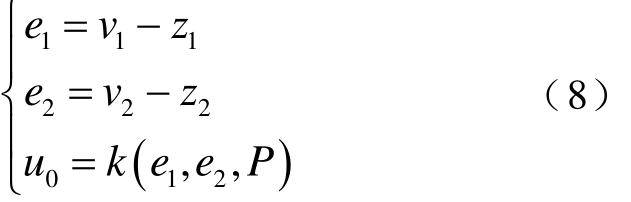
式中，P为反馈函数的参数集；k(e1,e2,P)为关于e1、e2、P的函数，可根据需要表示为多种反馈函数。
为避免出现高频颤振，本文反馈律采用引入阻尼因子的最速反馈综合函数u0=-fhan(e1,ce2,r,h1)，其中 c是阻尼因子，r是控制量的增益系数，h1是快速因子。
1.2.4 扰动估计补偿
ESO观测的扰动估计量z3和状态误差反馈控制量u0共同完成动态补偿线性化，从而实现不确定系统的实时动态线性化。
式中，b0为补偿因子。
1.3 自抗扰控制器分离性原理
自抗扰控制器涉及较多参数，从其结构和原理来看，TD、ESO和NLSEF独立实现各自功能，因此这三部分在设计过程中可以遵照“分离性原理”[14]对每个模块单独整定。一般先整定TD和ESO的参数，再对NLSEF和扰动估计补偿进行综合调整。
TD有v0、r0、h0和h四个参数。其中h取决于实际的仿真情况，大步长能减少计算量，缩短仿真时间，但步长过大会降低抑制噪声的能力。v0根据实际的控制目标进行选取。r0的取值影响到过渡过程的快慢，r0越大，TD跟踪速度越快，而跟踪速度就是过渡过程的微分值，因此r0过大会导致微分信号的振荡，一般取r0=10-4/h2。对于h0，只要满足h＜h0，便可消除稳态颤振。
ESO 有 α1、α2、δ、β01、β02、β03六个参数。αi的取值决定fal(e,α,δ)函数的非线性。δ取值过大，会使ESO的线性工作区增大，降低非光滑反馈的效果，减弱 ESO对非线性信号的逼近能力；δ取值过小，fal(e,α,δ)函数易在原点附近出现高频颤振。参数 α1、α2、δ对其他参数存在较大影响，因此优先整定，通常取 α1=0.5，α2=0.25，δ=h 时即可满足 fal(e,α,δ)函数的性能要求。参数 β01、β02、β03是状态误差反馈的反馈增益，影响ESO的观测效果。当基础参数α1、α2、δ、h确定后，线性ESO的反馈增益整定公式为β01≈1/h，β02≈1/(2.4h2)，β03≈1/(15.5h3)。
NLSEF有c，r，h1三个参数。根据控制效果进行调整，在合理的范围内，控制器性能对这些参数的波动不敏感，因此较易整定。ADRC控制器中仅补偿因子 b0的选取与被控对象有关，当被控对象未知的情况下，也可以将其估计至b的真值附近，ADRC控制器对b0的准确度要求较低，比较容易整定。
2 时滞在线估计
已知系统在第 i个时刻输出的无时滞信号为yc(ti)，经过时滞环节的反馈信号为y(ti)=yc(ti-δt)，其中δt表示时滞，将y(ti)以泰勒级数[21]展开得
仅保留等号右边前两项，式（10）可近似为
式（11）中y˙c(ti)可利用向后差分的方式近似求得，即
将式（12）代入式（11）中可得
其中
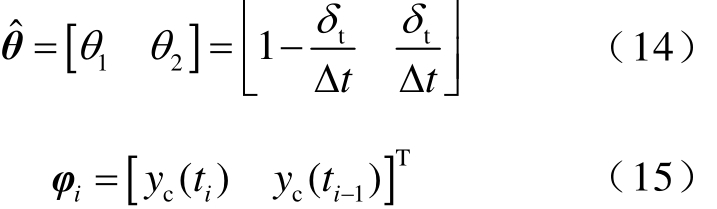
式（13）是关于θ1和θ2的线性函数，只需两组数据便可求得，并根据θ1和θ2计算系统中时滞为
可供选择的ˆθ求解方法众多，渐消记忆递推最小二乘法数据存储量小，计算量小，易满足在线估计的要求，其迭代格式为
式中，ρ为遗忘因子，0＜ρ＜1，不同取值代表不同遗忘效果，ρ越小，算法记忆渐消得越快，旧数据对最终估计值的影响越小，但是较小的ρ可能会造成估计值对新数据非常敏感，致使结果难以收敛。遗忘因子的选取要综合考量估计结果的收敛速度和辨识准确度，通过加入遗忘因子0.95≤ρ＜1，有助于提升递推算法的鲁棒性。该算法初始值可根据对前N组数据使用最小二乘法计算得到，也可以取
=0，P0=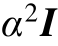
，其中α一般取104~106，I为单位矩阵[22]。
3 风电场广域附加阻尼控制
3.1 双馈风电场附加阻尼控制器
ADRC能够实时估计扰动并加以补偿，适用于各类不确定系统，然而反馈回路的时滞会影响控制器性能。因此，提出图2所示的SP-ADRC控制器，利用渐消记忆递推最小二乘法完成时滞的实时估计，以Smith预估器对时滞进行补偿，降低时滞对ADRC控制器性能产生的影响。设置的两个完全相同的带通滤波器，一是滤除低频振荡频率以外的噪声干扰，增强Smith预估器的抗干扰性；二是对反馈信号进行平滑处理以便提高时滞估计的准确度。
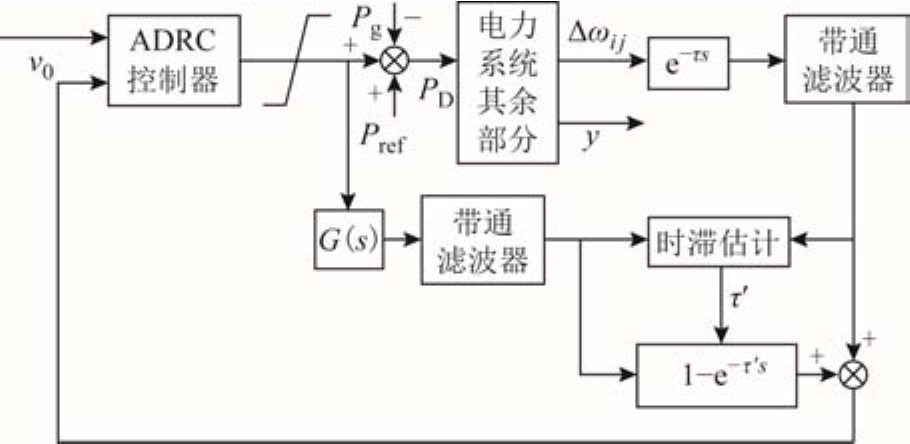
图2 SP-ADRC控制器框图
Fig.2 Block diagram of SP-ADRC controller
正常工作时，双馈风电机组处于最大功率点跟踪（Maximum Power Point Tracking, MPPT）模式；当系统中出现低频振荡时，将启动附加阻尼控制模式，以与区间振荡模式强相关机组i，j的转速差Δωij作为输入，经过自适应Smith预估器对反馈信号上的通信延迟进行补偿，再经过ADRC控制器和限幅等环节，输出叠加在双馈发电机组有功功率环以实现附加阻尼控制。图2中G(s)为被控对象的开环传递函数；Pref和Pg分别为双馈风电机组有功功率的给定值及相应的测量值；PD为叠加后的有功参考值；v0为预设的控制目标；y为系统其余的输出信号；τ和τ′分别为时滞的实际值和估计值。
3.2 SP-ADRC控制器设计步骤
基于 SP-ADRC的风电场广域附加阻尼控制器的设计步骤如下:
（1）通过模态分析，选取区间振荡模式主导机组的转速差Δωij作为SP-ADRC控制器的输入信号，并将ADRC的控制目标v0预设为0。
（2）利用Matlab辨识工具箱求得G(s)，将结果加入自适应Smith预估器，并选取合适的遗忘因子ρ和初始值
（3）利用1.3节介绍的分离性原理，整定ADRC控制器的参数。
4 仿真分析
利用DIgSILENT/PowerFactory仿真软件，以图3所示的10机39节点系统为例进行分析，参数见文献[23]。节点 16处的风电场由 20台 5MW 的双馈机组组成。
图3 新英格兰10机39节点系统
Fig.3 10- machine 39-bus New England system
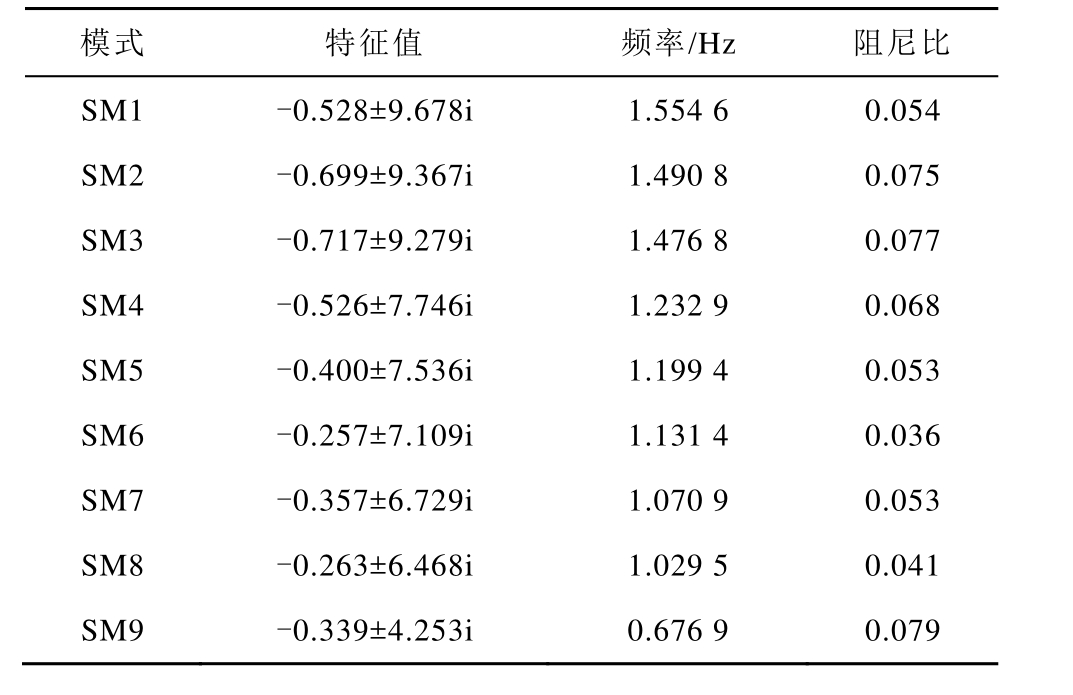
表1为系统机电振荡模式分析结果。其中模式SM9阻尼比较小，且其振荡频率最低，为0.676 9Hz，因此将SM9作为广域阻尼控制的主要抑制对象。
表1 含风电场的测试系统模态分析结果
Tab.1 Modal analysis results of test system with wind farm
模式 特征值 频率/Hz 阻尼比SM1 -0.528±9.678i 1.554 6 0.054 SM2 -0.699±9.367i 1.490 8 0.075 SM3 -0.717±9.279i 1.476 8 0.077 SM4 -0.526±7.746i 1.232 9 0.068 SM5 -0.400±7.536i 1.199 4 0.053 SM6 -0.257±7.109i 1.131 4 0.036 SM7 -0.357±6.729i 1.070 9 0.053 SM8 -0.263±6.468i 1.029 5 0.041 SM9 -0.339±4.253i 0.676 9 0.079
4.1 选取广域反馈信号
模式SM9的振荡模态如图4所示。从图4可以看出，SM9是G1相对于G2~G10°的区间振荡模式，其中G1的转速作为参考向量，G9转速的幅值仅次于G1，相位为-175.44°状态，因此选择G1和G9的转速差Δω19作为广域阻尼控制器的反馈信号。
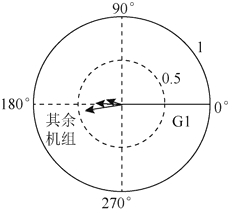
图4 模式SM9的振荡模态
Fig.4 Mode shape of SM9
4.2 控制器设计
利用DIgSILENT的模态分析法可知:图3所示系统的线性化模型阶次为287阶，难以通过物理建模的方法求解被控对象的开环传递函数。在双馈风电机组机侧有功功率控制信号上施加0.5s脉冲扰动，并以Δω19作为输出，采用 N4SID算法辨识得到被控对象不包含时滞环节的传递函数为G(s)=N(s)/D(s)，其中
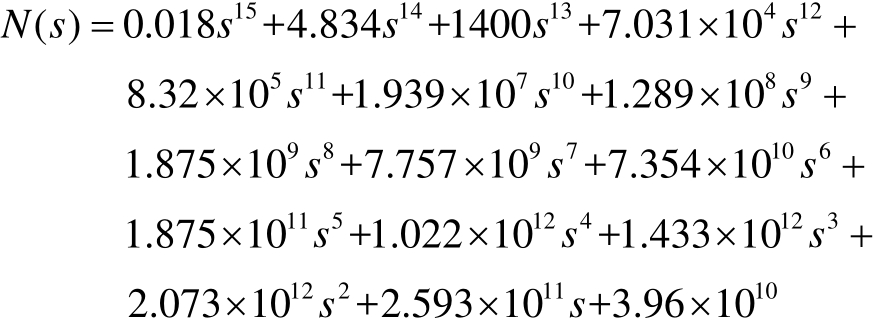
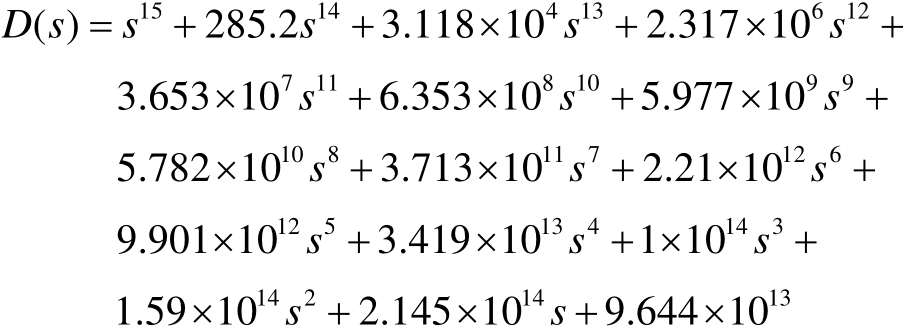
被控对象和辨识模型的响应曲线如图5所示。从图5可以看出，辨识模型在小扰动下的响应曲线很接近原系统响应曲线，能够保留系统的主要特征，因此可以使用该辨识模型进行控制器的设计。
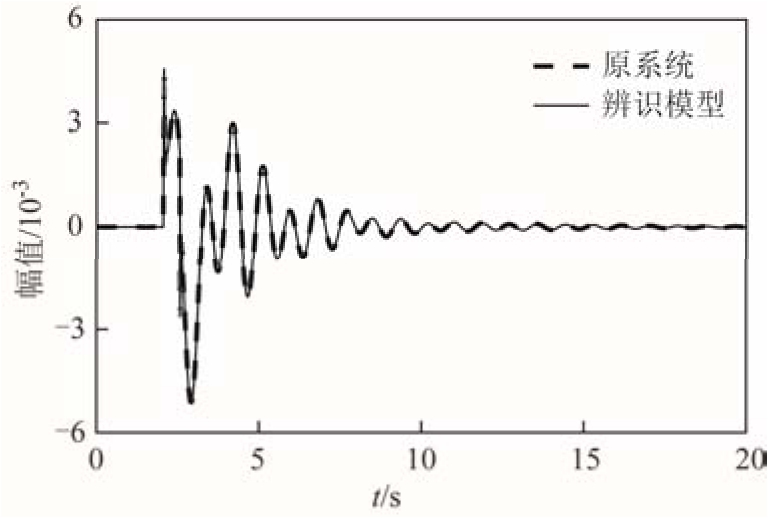
图5 脉冲响应曲线
Fig.5 Impulse response curves
根据1.3节中的思想对ADRC的参数进行整定，本文的仿真步长取为 0.01s，h0=0.05，r0=1，v0=0，β01=1/h =100，β02=1/(2.4h2)≈416 6.7，β03=1/(15.5h3)≈645 16.1，α1=0.5，α2=0.25，δ=h，c=0.5，r=3.6，h1=2，b0=100。通过对时滞估计算法的仿真调试，选取 ρ=0.98，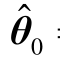
=0、α=1×106。
4.3 时域仿真
假设线路L4-14在2s时出现三相短路故障，0.1s后切除故障。采用Weibull分布的随机风速模型，平均风速为8.862m/s。仿真步长为0.01s，仿真时间为20s，仿真过程中SP-ADRC相关参数保持不变。
4.3.1 ADRC控制效果分析
为了考察 ADRC控制器抑制系统振荡的能力，略去图2控制策略中自适应Smith预估器部分。图6为不同时滞下的仿真结果，NC表示无控制。从图6可以看出，当无时滞时，ADRC控制器能够有效抑制系统振荡；当时滞为 60ms时，ADRC控制器仍能抑制低频振荡，但是振荡幅值和平息时间有所增加；当时滞为110ms时，系统出现等幅振荡，处于临界稳定状态。以上结果表明:①ADRC控制能有效提高系统阻尼，抑制低频振荡；②ADRC具有主动估计并补偿不确定因素的功能，能够承受一定范围内的时滞，但是随着时滞增加，ADRC控制器不再具备抑制振荡的能力。
图6 ADRC控制下的仿真曲线
Fig.6 Simulation curves under ADRC control
4.3.2 SP-ADRC控制性能验证
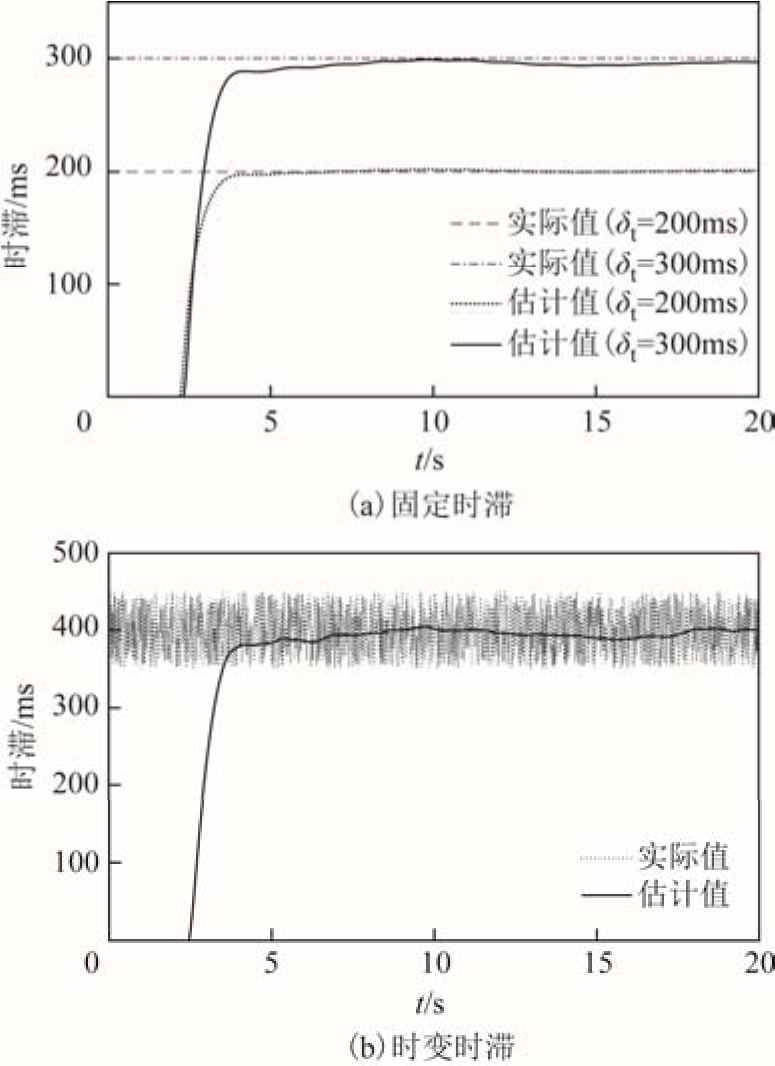
图7 多种时滞类型下的估计结果
Fig.7 Estimated results under a variety of types of time-delay
为检验本文控制策略在不同时滞下的控制效果，设置两种时滞条件:①固定时滞，200ms和300ms；②时变时滞，均值为400ms，在350~450ms内随机变化。渐消记忆递推最小二乘法对两种时滞情况的估计结果如图7所示。从图7可以看出，固定时滞的估计结果与实际值之间误差很小，时变时滞的估计结果接近其均值。由于本文忽略了时滞信号泰勒展开式的高阶项，当时滞较小时，忽略的部分影响很小；当时滞变大时，结果的误差会增加。对于时变时滞，由于算法对历史数据具有记忆性，且时变时滞的均值是400ms，因此估计值在均值附近波动。
图8为上述时滞条件下的仿真结果。从图8可以看出，ADRC控制器无法消除时滞的影响，当时滞较大时，其控制效果大大恶化，控制器失去阻尼作用，系统失去稳定。SP-PID控制器和 SP-ADRC控制器在不同时滞下都具备抑制系统振荡的能力，其中 SP-ADRC控制器下系统振荡幅值更小，可以更快地达到稳定状态。虽然渐消记忆递推最小二乘法对时滞的估计存在一定误差，但是由于ADRC本身具有较好的抗干扰性，可以承受一定范围内的时滞，因此 SP-ADRC控制器能够在各个时滞情况下更好地抑制振荡，具有较高的鲁棒性。
图8 多种时滞类型下的仿真曲线
Fig.8 Simulation curves under a variety of types of time-delay
事实上，因双馈风电场与 G1和 G9的距离不同，控制器输入信号ω1和ω9的时滞不同，因此需要分析多时滞情况下控制策略的有效性。为实现对两个信号回路上时滞的估计，采用图9所示的控制结构，在每个信号回路上均采用自适应Smith预估器，以实现对多个时滞的估计与补偿，其余设计步骤同上。
图9 DFIG附加阻尼控制框图
Fig.9 Additional damping control structure of DFIG
假设ω1带有300ms的时滞，ω9带有200ms的时滞，仿真结果如图10所示。从图10可以看出，相比于ADRC控制器和SP-PID控制器，SP-ADRC控制器依然具有较好的阻尼效果。说明SP-ADRC控制器可以更好地适应实际系统中的时滞情况。
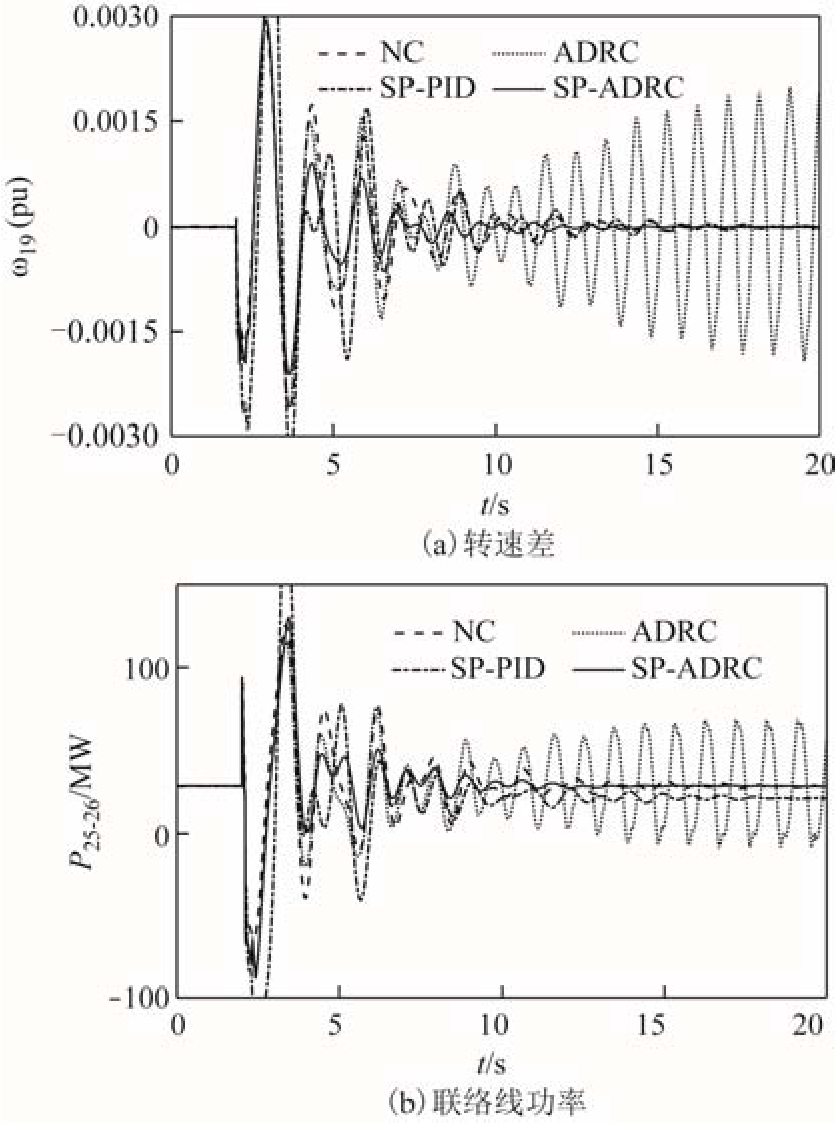
图10 多时滞下的仿真曲线
Fig.10 Simulation curves under multiple time-delay
5 结论
本文采用渐消记忆递推最小二乘法实现了具有不确定时滞的在线估计，基于此设计了SP-ADRC控制器。相比于传统的SP-PID附加阻尼控制，本文设计的 SP-ADRC附加阻尼控制器可以更好地适应不同的工况，改善系统阻尼，抑制低频振荡。当不考虑时滞影响的 ADRC控制器无法维持系统稳定时，考虑时滞影响的 SP-ADRC控制器仍然可以有效抑制系统中的区间振荡，多种时滞类型下不改变控制器参数，也验证了控制器的鲁棒性。
[1] Miao Zhixin, Fan Lingling, Osborn D, et al. Control of DFIG-based wind generation to improve interarea oscillation damping[J]. IEEE Transactions on Energy Conversion, 2009, 24(2): 415-422.
[2] Tsourakis G, Nomikos B M, Vournas C D.Contribution of doubly fed wind generators to oscillation damping[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 783-791.
[3] Aboul-Ela M E , Sallam A A , Mccalley J D , et al.Damping controller design for power system oscillations using global signals[J]. IEEE Transactions on Power Systems, 1996, 11(2): 767-773.
[4] Wu Hongxia, Tsakalis K S, Heydt G T. Evaluation of time delay effects to wide-area power system stabilizer design[J]. IEEE Transactions on Power Systems, 2004, 19(4): 1935-1941.
[5] 张子泳, 胡志坚, 刘宇凯. 计及广域信号时变时滞影响的大型双馈风力发电系统附加鲁棒阻尼控制[J]. 电工技术学报, 2014, 29(4): 246-255.Zhang Ziyong, Hu Zhijian, Liu Yukai. Additional robust damping control of large scale DFIG-based wind power generation system with wide-area signals’time-varying delay influence[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 246-255.
[6] Wang Shaobu, Meng Xiangyu, Chen Tongwen. Widearea control of power systems through delayed network communication[J]. IEEE Transactions on Control Systems Technology, 2012, 20(2): 95-103.
[7] Yao Wei, Jiang Lin, Wen Jinyu, et al. Wide-area damping controller of FACTS devices for inter-area oscillations considering communication time delays[J].IEEE Transactions on Power Systems, 2013, 29(1):318-329.
[8] 马燕峰, 张佳怡, 蒋云涛, 等. 计及广域信号多时滞影响的电力系统附加鲁棒阻尼控制[J]. 电工技术学报, 2017, 32(6): 58-66.Ma Yanfeng, Zhang Jiayi, Jiang Yuntao, et al.Additional robust damping control of wide-area power system with multiple time delays considered[J].Transactions of China Electrotechnical Society, 2017,32(6): 58-66.
[9] 姚伟, 文劲宇, 程时杰, 等. 考虑时滞影响的 SVC广域附加阻尼控制器设计[J]. 电工技术学报, 2012,27(3): 239-246.Yao Wei, Wen Jinyu, Cheng Shijie, et al. Design of wide-area supplementary damping controller of SVC considering time delays[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 239-246.
[10] 李婷, 吴敏, 何勇. 计及广域测量系统时滞影响的灵活交流输电系统阻尼控制器多目标设计[J]. 电工技术学报, 2014, 29(8): 227-234.Li Ting, Wu Min, He Yong. Multi-objective design of FACTS damping controller based on WAMS with signal transmission delay[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 227-234.
[11] Watanabe K, Ito M. A process-model control for linear systems with delay[J]. IEEE Transactions on Automatic Control, 1981, 26(6): 1261-1269.
[12] 王伟岸, 王俊, 蔡兴国. 基于史密斯预估器的互联电网区间阻尼控制[J]. 电力系统自动化, 2008,32(20): 37-41.Wang Weian, Wang Jun, Cai Xingguo. Damping control of interconnected power system based on smith predictor[J]．Automation of Electric Power Systems, 2008, 32(20): 37-41.
[13] Chaudhuri B, Majumder R, Pal B C. Wide-area measurement-based stabilizing control of power system considering signal transmission delay[J]. IEEE Transactions on Power Systems, 2004, 19(4): 1971-1979.
[14] 韩京清. 自抗扰控制技术:估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
[15] 盖江涛, 黄守道, 黄庆, 等. 基于负载观测的永磁电机驱动系统自抗扰控制[J]. 电工技术学报, 2016,31(18): 29-36.Gai Jiangtao, Huang Shoudao, Huang Qing, et al.Active-disturbance rejection controller for permanent magnet motor drive system control based on load observer[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 29-36.
[16] 杜博超, 韩守亮, 张超, 等. 基于自抗扰控制器的内置式永磁同步电机无位置传感器控制[J]. 电工技术学报, 2017, 32(3): 105-112.Du Bochao, Han Shouliang, Zhang Chao, et al.Sensorless control of interior permanent magnet synchronous motor based on active disturbance rejection on controller[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 105-112.
[17] 曾岳南, 曾祥彩, 周斌. 永磁同步电机传动系统电流环非线性自抗扰控制器的设计与稳定性分析[J].电工技术学报, 2017, 32(17): 135-143.Zeng Yuenan, Zeng Xiangcai, Zhou Bin. Nonlinear active disturbance rejection controller design for current loop of PMSM drive system and its stability analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 135-143.
[18] 马燕峰, 周一辰, 刘海航, 等. 一种基于自抗扰控制的多机低频振荡本地控制方法[J]. 中国电机工程学报, 2017, 37(5): 1360-1372.Ma Yanfeng, Zhou Yichen, Liu Haihang, et al. A local control method of multi-machine low frequency oscillation based on active disturbance rejection control[J]. Proceedings of the CSEE, 2017, 37(5):1360-1372.
[19] 马燕峰, 蒋云涛, 陈磊, 等. 光伏电站自抗扰附加阻尼控制抑制低频振荡策略研究[J]. 电网技术,2017, 41(6): 1741-1747.Ma Yanfeng, Jiang Yuntao, Chen Lei, et al. An ADRC additional damping control strategy research on low frequency oscillation suppression of photovoltaic plants[J]. Power System Technology, 2017, 41(6):1741-1747.
[20] 马燕峰, 刘会强, 俞人楠. 风电场中 STATCOM 抑制系统功率振荡[J]. 电力自动化设备, 2018, 48(2):67-73.Ma Yanfeng, Liu Huiqiang, Yu Rennan. Power oscillation suppression based on STATCOM in wind farms[J]. Electric Power Automation Equipment, 2018,48(2): 67-73.
[21] 王贞, 吴斌. 基于最小二乘法的时滞实时在线估计方法[J]. 振动工程学报, 2009, 22(6): 625-631.Wang Zhen, Wu Bin. A real-time approach to delay estimation based on the least-square algorithm[J].Journal of Vibration Engineering, 2009, 22(6): 625-631.
[22] 刘栋良, 任劲松, 林伟杰, 等. 基于电感辨识的电流解耦算法在内置式永磁同步电机弱磁控制中的应用[J]. 电工技术学报, 2017, 32(16): 98-105.Liu Dongliang, Ren Jinsong, Lin Weijie, et al. Current decoupling algorithm based on inductance identification in the application of interior permanent magnet synchronous motor flux-weakening control[J].Transactions of China Electrotechnical Society, 2017,32(16): 98-105.
[23] Pai M A. Energy function analysis for power system stability[M]. Dordrecht: Kluwer Academic Publishers,1989.