0 引言
近年来大规模风电机群接入电网引发的次同步振荡（Subsynchronous Oscillation, SSO）问题得到了广泛关注，典型事件如河北沽源地区风电场（以双馈风机为主）经串补输电线路并网后多次发生频率在 3~10Hz的次同步功率振荡，新疆哈密地区风电场（以直驱风机为主）接入弱交流电网后多次出现20~30Hz的次同步功率振荡[1]。与传统的次同步谐振、扭振相互作用问题的特征不同，风电并网系统的次同步功率振荡的频率存在较大幅度的动态变化，主要体现为同一风电场各次事件的振荡频率不同和一次事件中振荡频率的不断演化。因此，频率漂移是风电并网系统次同步振荡的显著特征，研究和揭示频率漂移的内在机理将有助于防范风电并网引发的次同步振荡失稳的风险。
现有关于风电并网系统次同步振荡机理的研究已经开展了较多，从研究对象来划分，以双馈风机-串补输电系统[2-10]和直驱风机-弱交流电网系统[11-13]为主；从分析方法来划分，主要包括频域分析法[2-3,8-9,11-13]和模式分析法[2,5-7,10-11]。这些研究分析了风电机组的动态特性、剖析了次同步振荡的主要影响因素、刻画了次同步振荡稳定性的参数条件。
虽然目前大量文献呈现了多种因素对次同步振荡阻尼和频率的影响规律，但是并未对频率漂移的现象给出进一步的机理解释。文献[2]针对双馈风机-串补输电系统，采用时域仿真、模式分析和等效电路研究了并网风机数量、风速、线路参数和换流器控制参数对次同步振荡阻尼和频率的影响。文献[3]基于聚合RLC电路的阻抗分析方法研究双馈风机-串补输电系统的阻抗频率特性。文献[7]结合概率法和模式分析法，研究多运行方式下风电串补系统的次同步振荡特性。文献[11]针对直驱风机-弱交流系统，采用模式分析、时域仿真和阻抗分析法研究电网强度、并网风机数量、网侧换流器控制参数对次同步交互特性的影响。然而，对于实际运行的电力系统，线路参数和换流器控制参数往往是固定的，从风速和并网风机数量的角度研究次同步振荡频率漂移现象可能更具有实际意义。那么这些频率漂移现象内在的规律是否有所关联以及是否存在统一的机理，是本文研究的出发点和所要解决的关键问题。
开环模式分析方法[14-17]从模式相互作用的观点解释了风电并网系统次同步振荡的现象:当一台风电机组的开环振荡模式靠近系统中其他动态元件的开环振荡模式时，相应的两个闭环振荡模式将会发生互斥，从而导致其中一个闭环振荡模式的阻尼减弱，文献[14-17]将这种模式相互作用称之为开环模式耦合。文献[14-17]的算例结果表明换流器控制参数、输电网络拓扑结构的参数、风电机组的输出功率会影响开环模式耦合条件，进而引发次同步振荡。然而，这些文献并不以频率漂移问题为研究重点，对频率漂移问题的机理解释仍需深入探讨。
考虑到风速的随机性，风电机组的运行点会发生变化，由此导致风电机组的动态特性在不同时间点下的差异，这也体现为风电机组的开环振荡模式和留数的波动。因此，风速变化可能为开环模式耦合提供条件，从而出现次同步振荡频率漂移的现象。本文将从风速变化导致开环模式耦合的角度揭示风电并网系统次同步振荡频率漂移的机理。
1 机理分析
1.1 与风速相关的风电机组次同步振荡模式
根据文献中的相关结论，风电并网系统次同步振荡弱阻尼或负阻尼的模式源于:①双馈风机（Doubly-Fed Induction Generator, DFIG）定转子绕组和转子侧换流器（Rotor-Side Converter, RSC）电流内环控制主导的次同步振荡模式[2,5-6]；②直驱风机（Direct-Drive Permanent Magnetic Synchronous Generator, D-PMSG）网侧换流器（Grid-Side Converter, GSC）直流电压外环控制主导的次同步振荡模式[11]。本节推导并论证风速对这两个次同步振荡模式的影响。
1.1.1 DFIG定转子绕组和RSC电流内环控制主导的振荡模式（EMO模式）
文献[5-6]指出 DFIG机组存在一个频率与转子转速相关的振荡模式，本文记该模式为EMO模式。在dq旋转坐标系下，EMO模式的频率会随着风速的减小而增大。但是文献[5-6]中并未推导 EMO模式的来源。本小节给出具体推导过程。
DFIG异步发电机的动态特性由定转子绕组动态表征，在dq旋转坐标系下以矢量形式表示的电压方程和磁链方程为[18]
式中，U s为发电机端口电压；U r为RSC输出电压；Is 和Ir分别为定、转子电流；ψs和ψr分别为定、转子磁链， 
和 R r分别为定、转子电阻；Ls和 L r分别为定、转子自感；Lm为互感；ω1为dq同步旋转坐标系的角速度，即同步速；ωr为转子转速。
根据式（1），在复频域下定转子电压、电流关系可表示为
其中
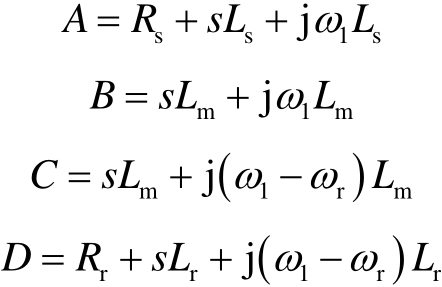
不考虑RSC外环动态，RSC输出电压 rU为
式中，rrefI 为转子电流参考值；p_irk 和 i_irk 分别为RSC电流内环控制环节的比例、积分系数；s为拉普拉斯算子。
忽略转子动态过程，将式（3）代入到式（2）中并线性化，可得
式中，Δ表示增量。
根据式（4），特征方程为
特征方程的根即为定转子绕组和 RSC电流内环控制主导的振荡模式。文献[5-6]中描述的EMO模式即源于此，下面对EMO模式展开详细讨论。
考虑定子电阻 sR较小，忽略其影响，将式（5）进一步写成
式中，
当不考虑 RSC电流内环控制时， 
式（6）的特征根为（求解过程参见附录）
当考虑RSC电流内环控制时，式（6）的特征根为（求解过程参见附录）
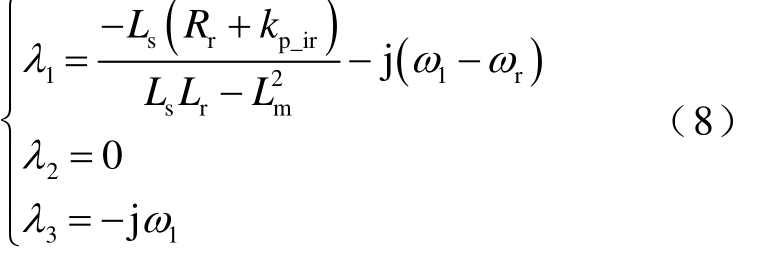
根据式（7）和式（8），1λ即为EMO模式，频率与转子转速rω相关。由于DFIG采用最大风功率跟踪控制，风速与转子转速存在对应关系。因此在不同风速下 EMO模式的频率存在动态变化范围。若接近其他动态元件的振荡模式，两个模式将会发生强交互作用，导致闭环振荡模式阻尼的下降和频率的漂移。
1.1.2 网侧换流器直流电压外环主导的振荡模式
D-PMSG和DFIG的网侧换流器相似，为了便于后文分析，本节推导D-PMSG网侧换流器直流电压外环控制主导的振荡模式，而 DFIG推导过程基本一致，不再赘述。
D-PMSG并网系统的结构和控制框图参见文献[16]。记 dq旋转坐标系下 D-PMSG网侧换流器的输出电压为 cdV 和 cqV ，输出电流为 cdI和 cqI，并网点电压为 gdV 和 gqV 。假设锁相环（Phase Locked Loop,PLL）理想，不存在锁相误差。dq旋转坐标系的 d轴定向于并网点电压，即
d轴输出电流的线性化动态方程为
式中， fX为GSC出口滤波电抗。
d轴电流内环PI控制的线性化动态方程为
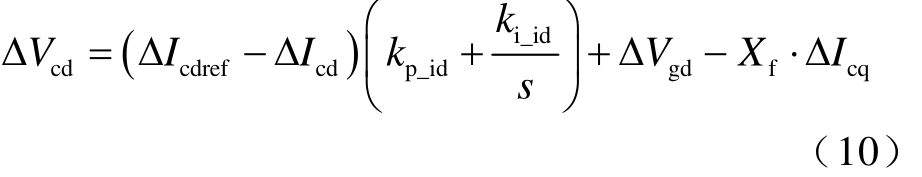
式中，cdrefIΔ为D-PMSG网侧换流器d轴输出电流参考值的的微增量； p_idk 和 i_idk 分别为GSC网侧换流器电流内环控制环节的比例、积分系数。
将式（10）代入到式（9）中，可得
d轴直流电压外环PI控制的线性化动态方程为
式中，dcVΔ为直流电容电压微增量；p_dck和i_dck分别为GSC直流电压外环控制环节的比例、积分系数。
直流电容的线性化动态方程为
式中，下标0表示相应变量的稳态值；C为直流电容； gP为网侧换流器输出有功功率。
结合式（11）~式（13），D-PMSG输出电流和并网点电压的传递函数为
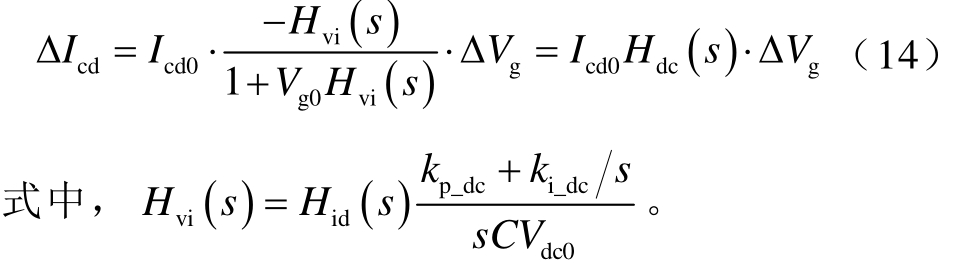
根据式（14），直流电压外环控制主导的振荡模式为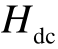 
(s)的极点，留数大小与
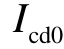有关。而由于DPMSG采用单位功率因数控制，D-PMSG输出电流的 q轴分量 Ic q 0=0，D-PMSG输出电流的 d轴分量等于电流幅值 I c d 0 = Ic0。这表明，不同风速下 DPMSG输出有功功率的大小直接影响着直流电压外环控制模式的留数的大小，并且输出有功功率越大，直流电压外环控制模式与其他模式的交互作用程度越强。
1.2 开环模式耦合与闭环模式互斥
文献[14-17]将闭环系统拆分为两个互联的开环子系统，建立了单变量系统的闭环互联模型，根据一维的留数信息提出了闭环振荡模式的评估方法。而本文研究的风电并网系统为多变量系统，以所研究的风电机组作为一个子系统，其余部分作为另一个子系统，以接口电压、电流作为交互物理量，构建双输入双输出的闭环互联模型，最终提出开环模式耦合条件下基于二维的留数矩阵评估闭环振荡模式的方法。
1.2.1 双输入双输出系统的闭环互联模型
为了便于稳定性研究，考虑风电场的聚合等值模型以一台风电机组表征，在公共旋转坐标系下风电机组的输出电流为
端口电压为
将风电机组作为一个子系统，输入为端口电压，输出为电流，传递函数为
系统其余部分作为另一个子系统，输入为电流，输出为电压，传递函数为 
构建闭环互联模型，如图1所示。
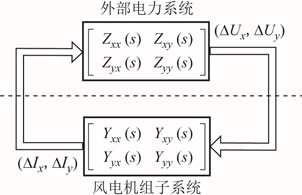
图1 双输入双输出闭环互联模型
Fig.1 Closed-loop interconnected model with two input and two output
以状态空间的形式表示图1所示的闭环互联模型，其中，风电机组子系统的状态空间模型为
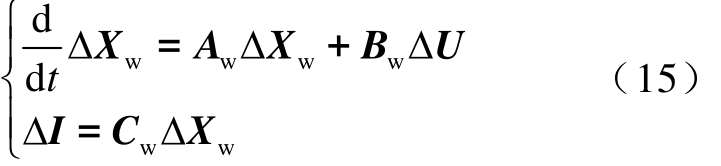
式中，Aw、Bw、Cw分别为风电机组子系统状态空间方程的状态矩阵、输入矩阵和输出矩阵；ΔXw为风电机组子系统的状态变量，且
外部电力系统的状态空间模型为
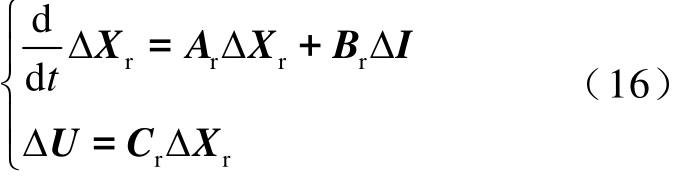
式中，Ar、Br、Cr分别为外部电力系统状态空间方程的状态矩阵、输入矩阵和输出矩阵；ΔXr为外部电力系统的状态变量，且
1.2.2 闭环模式评估方法
根据1.2.1节的建模过程可知，两个子系统的交互物理量为二维，文献[14-17]中单变量系统的闭环模式评估方法不再适用。本节推导开环模式耦合条件下双输入双输出系统的闭环模式评估方法。
记风电机组子系统的某个开环振荡模式为wλ，亦即 wA的其中一个特征值， ww和 wv为相应的左、右特征向量，对应的留数矩阵[19]为
记外部电力系统的某个开环振荡模式为rλ，亦即 rA的其中一个特征值， rw和 rv为相应的左、右特征向量，对应的留数矩阵为
风电机组子系统和外部电力系统的开环传递函数 Y (s )和Z ( s)可以用留数和开环模式的形式表征为
式中，λwj为Aw除了λw之外的特征值，在每个传递函数矩阵元素中对应的留数分别为
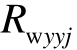，亦即留数矩阵Rw中的元素；λri为Ar除了λr之外的特征值，在每个传递函数矩阵元素中对应的留数分别为
亦即留数矩阵Rr中的元素。
在开环模式耦合条件 λ w ≈λr下，相应的闭环振荡模式 λˆ w和λˆr与开环振荡模式满足关系（推导过程见附录）
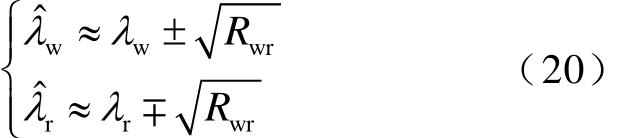
式中，
式（20）表明在开环模式耦合条件下，两个闭环振荡模式将会发生互斥——相对于开环振荡模
的位置向两侧偏移
，导致其中一个闭环振荡模式的阻尼变差，并且互斥程度与留数矩阵有关。
根据上述理论分析，在风速变化过程中由于DFIG的EMO模式的频率也会发生变化，EMO模式有可能逐次接近系统中其他动态元件主导的次同步振荡模式进而导致闭环模式间发生强相互作用，从而出现不同频段下的次同步功率振荡，如图2所示。另外，由于闭环模式互斥程度与留数有关，DPMSG直流电压外环主导的次同步振荡模式在不同风速下与其他模式发生相互作用的程度将会发生变化，从而影响了闭环振荡模式的阻尼和频率，同样可能引发次同步振荡频率漂移的现象。这些猜想将在第2节采用具体算例进行验证。
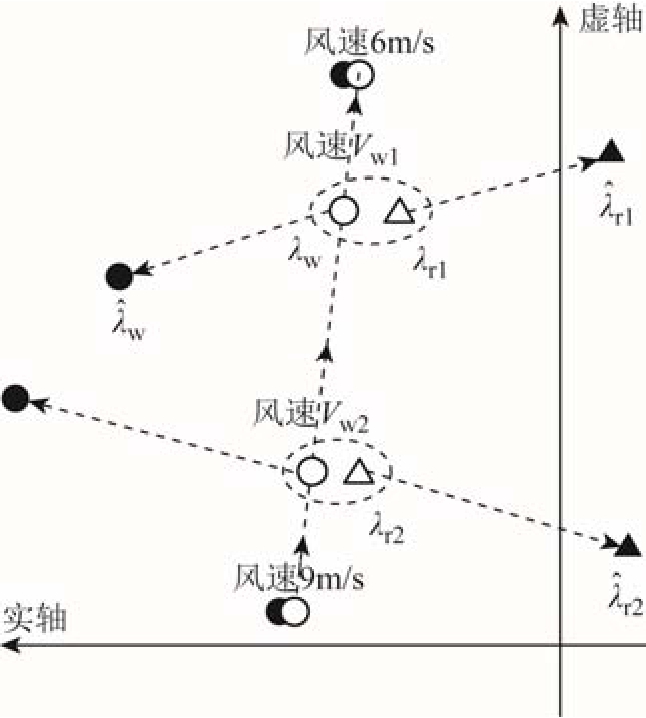
图2 模式相互作用
Fig.2 Modal interaction
2 算例分析
2.1 DFIG-串补输电系统的频率漂移问题
DFIG的动态特性受风速波动的影响，如 1.1.1节所述，EMO模式的频率可能会发生较大范围的变化，这决定了 EMO模式和串补振荡模式之间相互作用的强弱程度也是动态变化的，由此可能导致频率漂移的现象。
本节研究 DFIG-串补输电系统次同步振荡的频率漂移问题，系统结构如图3所示。DFIG风电场包括50台同型机组，采用单机聚合等值模型，详细模型和参数参见文献[20]，DFIG模型为 20阶，计及轴系、定转子绕组、DC环节、RSC控制、GSC控制、GSC出口滤波电抗、PLL控制环节的动态。固定串补度为0.36。由于换流器采用最大风功率跟踪控制，风速、转子转速参考值、风电机组机械功率之间存在对应关系，参见文献[20]。将DFIG和串补输电线路作为两个子系统，构建闭环互联模型，如图1和图3所示。
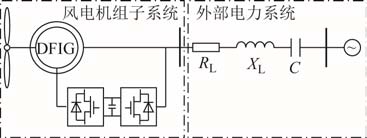
图3 DFIG-串补输电系统
Fig.3 Diagram of DFIG connected to a series-compensated system
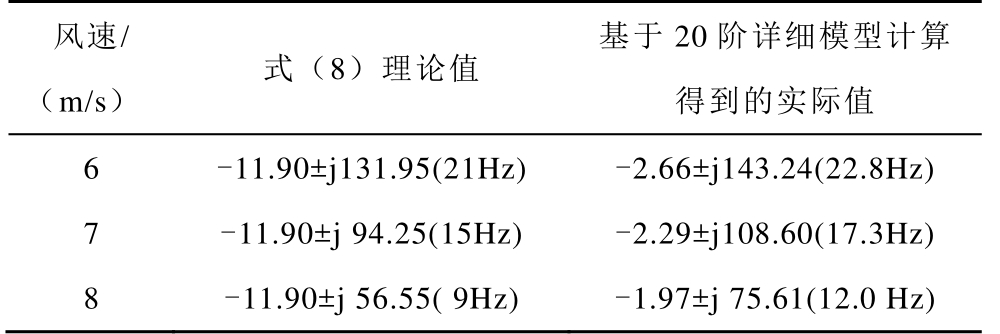
首先，需要指出的是，当考虑了转子动态后，基于详细模型计算得到的EMO模式将会与1.1.1节中式（6）~式（8）的理论分析结果不同，但是EMO模式的频率随风速变化的趋势是相同的，表 1对此进行了演示说明。表 1中第 2列为忽略转子动态、基于式（8）计算得到的不同风速下的EMO模式的理论值。表1中第3列为基于20阶详细模型计算得到的EMO模式的实际值。对比可见，在忽略转子动态的情况下，式（8）的理论值结果与考虑转子动态的详细模型的模式分析结果的误差在一定范围内可以接受，对振荡频率随风速变化的规律的描述比较一致，因此，1.1.1节的理论分析能够合理地描述EMO模式的频率特征——随着风速的减小，DFIG的EMO模式的频率增大。这将作为下面算例分析中讨论风速变化引起的模式相互作用机理的理论基础之一。（后文的模式分析、仿真分析中，都是基于风电机组的详细模型展开讨论。）
表1 不同风速下EMO模式的理论值和实际值对比
Tab.1 Comparision of the theoretical and actual values of EMO mode at different wind speeds
风速/（m/s）式（8）理论值基于20阶详细模型计算得到的实际值6 -11.90±j131.95(21Hz) -2.66±j143.24(22.8Hz)7 -11.90±j 94.25(15Hz) -2.29±j108.60(17.3Hz)8 -11.90±j 56.55( 9Hz) -1.97±j 75.61(12.0 Hz)
在风速由 8m/s减小到 6m/s的过程中，转子转速参考值由 0.85(pu)减小到 0.65(pu)，DFIG的开环EMO模式λw由-1.97+j75.61变化到-2.66+j143.24，如图4a中空心圆所示。外部电力系统的开环振荡模式为开环串补振荡模式λr=-9.05+j150.98，如图4a中空心三角形所示。在风速减小的过程中，λw不断接近λr，根据闭环状态空间模型，计算闭环模式 
和
，分别如图4a中实心圆和实心三角形所示，闭环振荡模式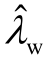 
和
的模式相互作用程度不断增强，呈现出互斥特征: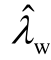
的阻尼大幅增加，而
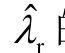r的阻尼急剧减小为负。在开环模式耦合条件 λ w ≈ λr 下，
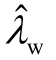和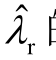
的互斥程度最显著。根据式（20）计算得到的闭环模式的估计值如图4a中叉号所示，其中
可见，开环模式耦合条件下闭环模式的估计值和实际值比较接近，本文所提的闭环模式评估方法能够较准确地评估闭环模式。
图4 不同风速下DFIG与串补输电系统的模式相互作用
Fig.4 Modal interaction between DFIG and seriescompensated system with the variation of wind speed
在模式相互作用过程中，不仅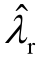 
的阻尼不断减弱，其频率也由23.90Hz变化到26.25Hz，次同步振荡的频率发生了漂移，如图4b所示。
2.2 混合风电场并网系统的频率漂移问题
混合风电场并网系统的结构如图5所示。风电场包含50台DFIG和50台D-PMSG。其中，DFIG的聚合等效模型采用单机表征方法，模型和参数参见文献[20]；D-PMSG聚合等效为 D-PMSG1和 DPMSG2，分别包含 25台机组，模型和参数参见文献[21-22]。D-PMSG1和D-PMSG2的直流电压外环控制参数
存在差异，分别为(0.06,15)和(0.13,50)。将 DFIG作为一个子系统，D-PMSG1、D-PMSG2和输电线路作为另一个子系统，构建闭环互联模型，如图1和图5所示。
图5 单DFIG-双D-PMSG风电场并网系统
Fig.5 A DFIG and two D-PMSGs based wind farm connected power system
2.2.1 情形1
不失一般性，情形1假设D-PMSG机组风速恒定且输出额定功率，DFIG机组考虑风速波动的影响。D-PMSG1和D-PMSG2存在直流电压外环主导的开环次同步振荡模式r1λ和r2λ。在DFIG机组输出功率波动过程中r1λ和r2λ的变化较小，r1λ≈-2.18+j45.46，r2λ≈-1.74+j82.78，如图6a中空心三角形和空心菱形所示。在DFIG机组的风速由9m/s减小到6m/s的过程中，DFIG的开环EMO模式wλ由-1.92+j20.80变化到-0.09+j107.01，如图6a空心圆所示。可见，在风速为8m/s时，wλ和r1λ满足开环模式耦合条件，根据式（20）计算得到的闭环振荡模式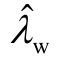
和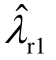
的估计值如图6a叉号所示，根据闭环状态空间模型计算得到的闭环振荡模式
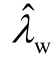和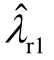
如图6a中实心圆和实心三角形所示。在开环模式耦合条件下，闭环振荡模式发生互斥，并且，闭环振荡模式的估计值与实际值比较接近，验证了 1.2节所提闭环模式评估方法的正确合理性。根据图6a，
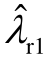偏移到复平面的右半平面 
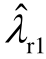=0.27+j43.41，系统存在次同步振荡失稳的风险，振荡频率为6.91Hz。当风速变化到6.8m/s时，
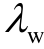和λr2满足开环模式耦合条件，闭环振荡模式的估计值如图6a中十字所示；闭环振荡模式的实际值
和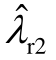
发生互斥，如图6a中实心圆和实心菱形所示。
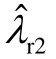偏移到复平面的右半平面 
=1.94+j78.15，系统存在次同步振荡失稳的风险，振荡频率为12.44Hz。
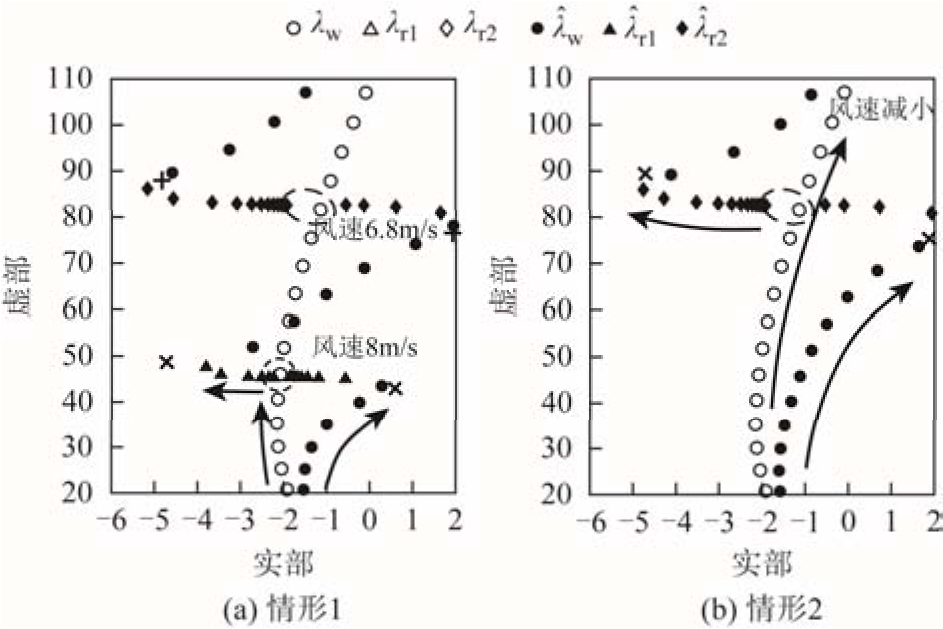
图6 不同风速下DFIG与D-PMSG1、D-PMSG2的模式相互作用
Fig.6 Modal interaction between DFIG and D-PMSG1,D-PMSG2 with the variation of wind speed
根据图6a，风速的减小使得λw的频率不断增大，从而导致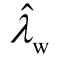
依次和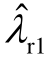
、
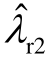发生强的模式相互作用，出现不同频率的负阻尼的闭环振荡模式，亦即次同步振荡频率漂移的现象。图7描述了风速变化过程中负阻尼次同步振荡模式的频率和阻尼。当风速在7.95~8.10m/s范围内时，
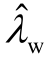和
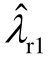的强交互作用导致次同步振荡失稳，频率为 6.7~7.0Hz；当风速在6.25~7.15m/s范围内时
和
的强交互作用导致次同步振荡失稳，频率为11.2~13.1Hz。
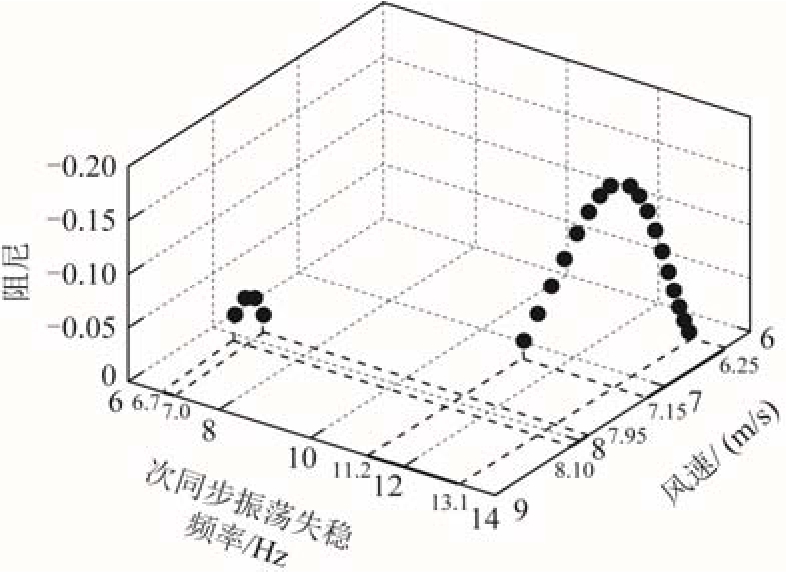
图7 风速与次同步振荡失稳频率的关系
Fig.7 Connection of wind speed and the frequency of undamped subsynchronous oscillation
下面采用非线性仿真验证模式分析的结论。在仿真时间 t=0.1s时并网点电压瞬时跌落 10%，对比风速分别为9m/s（非开环模式耦合条件）、8m/s（开环模式耦合条件
和6.3m/s（开环模式耦合条件
的情况下D-PMSG1、D-PMSG2和DFIG输出的有功功率，非线性仿真结果如图8所示。结果表明，在风速为6.3m/s时，DFIG和D-PMSG2之间存在不利的交互作用，DFIG和D-PMSG2的有功功率振荡发散，振荡频率为13Hz，由于D-PMSG1不是参与开环模式耦合的主导元件，因此D-PMSG1的有功功率波动相对 D-PMSG2较小；在风速为8m/s时，DFIG和D-PMSG1之间存在不利的交互作用，导致 DFIG和 D-PMSG1的有功功率振荡发散，振荡频率为 7Hz，由于 D-PMSG2不是参与开环模式耦合的主导元件，因此 D-PMSG2的有功功率波动相对较小；在风速为9m/s时，不满足开环模式耦合条件，DFIG与D-PMSG之间的交互作用较弱，风电机组输出有功功率振荡收敛。非线性仿真结果与模式分析结论一致。
2.2.2 情形 2
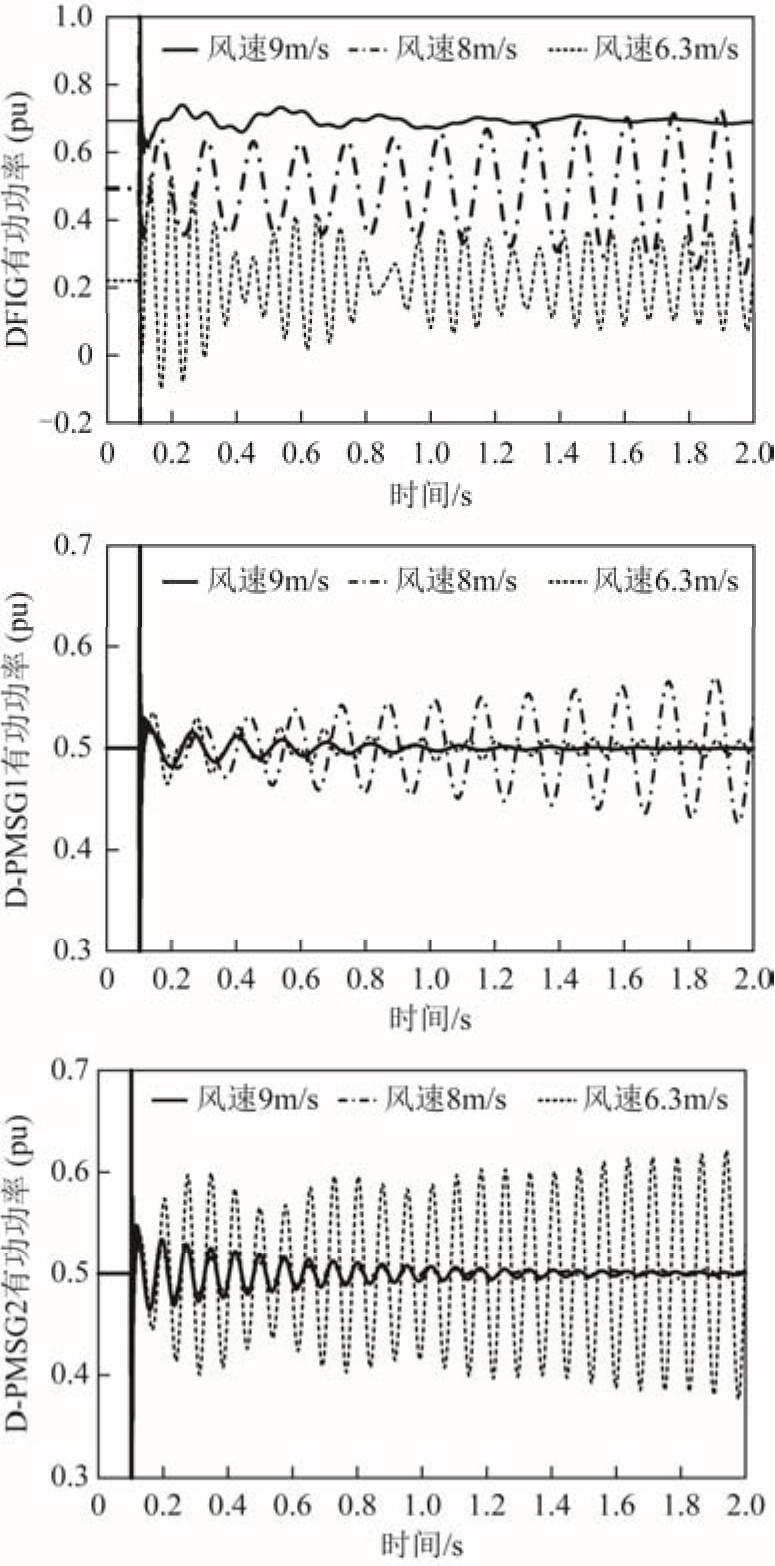
图8 非线性仿真结果
Fig.8 Simulation results
若将 D-PMSG1的直流电压外环的积分系数由15调整为1，此时随风速变化的开、闭环振荡模式轨迹如图6b所示。对比图6a，在风速8m/s范围内，由于 λr1消失，
和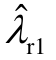
的交互作用得以消除，6.7~7.0Hz频率的次同步振荡失稳现象将不会发生。这进一步说明了模式间不利的强相互作用会引发次同步振荡失稳。
2.2.3 情形3
不同于情形 1和情形 2，本节假设 DFIG的风速不变，D-PMSG的风速发生变化，从而D-PMSG输出的有功功率和电流也会随之改变。根据1.1.2节的分析，D-PMSG直流电压外环主导的次同步振荡模式及其留数与输出电流有关。基于此，本节研究D-PMSG2的风速变化对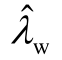
和
之间的模式相互作用的影响。
随着风速的增大，D-PMSG2中单台机组输出的有功功率从 0.1MW 增加到 2MW，D-PMSG2直流电压外环主导的振荡模式r2λ从-0.48+j82.89变化到-2.31+j82.87，如图9中空心菱形。而潮流的变化对wλ的影响不大，wλ≈-1.25+j81.68，如图9中空心圆所示。可以看出，在整个风速变化过程中一直保持开环模式耦合条件 λ w ≈λr2，而模式相互作用随着风速增大而趋于显著，如图9所示，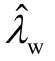
和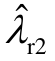
互斥的程度不断加剧，导致闭环振荡模式
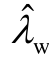的阻尼由正变负，频率由13Hz变化到12.4Hz。这是由于λr2的留数随着 D-PMSG2输出电流的增加而增大，基于式（17）计算的留数矩阵 R w的结果如图10所示。根据式（20）， R w元素的增大导致开、闭环振荡模式的偏移量
的增大，从而出现了闭环振荡模式的阻尼和频率发生漂移的现象。
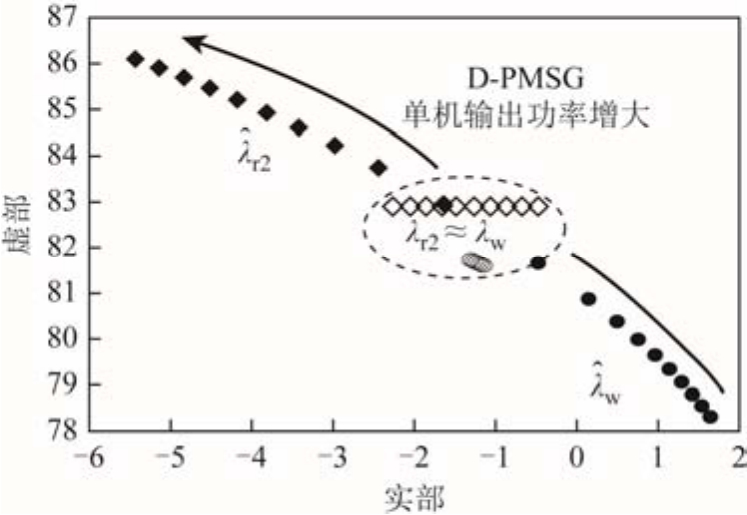
图9 不同风速下D-PMSG2与DFIG的模式相互作用
Fig.9 Modal interaction between D-PMSG2 and DFIG with the variation of wind speed
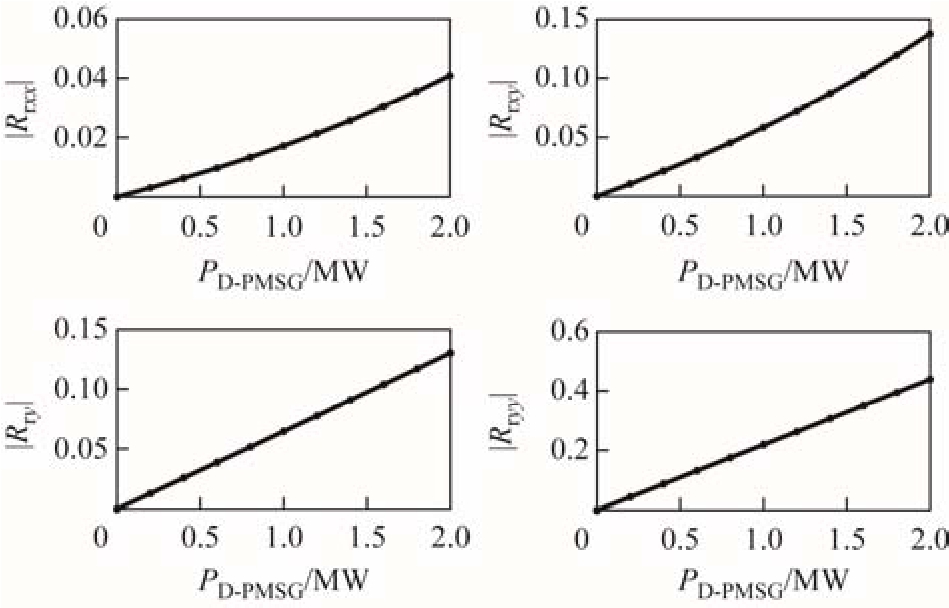
图10 D-PMSG单机输出功率对留数矩阵元素的影响
Fig.10 Elements of residue matrix under different output active power of single D-PMSG
三种不同情形的分析结果说明，风速变化会影响风电机组开环振荡模式的阻尼和频率，如DFIG的 EMO模式和 D-PMSG的直流电压外环控制振荡模式，这将可能为开环模式耦合提供条件，引发模式间不利的强交互作用，导致闭环振荡模式的阻尼大幅下降。由于实际系统中风速的随机性，风电机组可能在不同风速下与不同的控制环节发生不利的强交互作用，从而导致不同频率的次同步功率振荡，如情形1下DFIG在风速变化过程中依次与D-PMSG1和D-PMSG2发生强交互。另外一种情况，DFIG和D-PMSG的不同风速组合所表现出的模式相互作用的特性会存在差异，如情形1中DFIG风速为6.8m/s时DFIG和D-PMSG2之间存在强交互作用，而此时若D-PMSG2单机输出功率减小，如情形3，DFIG和D-PMSG2之间的强交互作用将会减弱甚至消失，从而消除次同步振荡失稳现象。因此，对于风电并网系统，风速的随机性使得开环模式耦合条件也具备了随机性，在时变场景下模式间的不利交互作用使得弱阻尼或负阻尼次同步振荡模式的频率是动态变化的，由此出现了频率漂移的现象。
3 结论
本文从风速变化影响开环模式耦合条件的角度解释了风电并网系统次同步振荡频率漂移的原因，得到的主要结论如下:
1）DFIG存在一个由定、转子绕组和RSC电流内环控制主导的 EMO模式，该模式的频率与转子转速相关。DFIG或D-PMSG中存在一个由网侧换流器直流电压外环控制主导的振荡模式，该模式的留数与网侧换流器输出电流大小有关。这两种次同步振荡模式与风速密切相关。
2）风速会改变DFIG EMO模式的频率，进而影响DFIG EMO模式与串补振荡模式间的交互作用的程度。在强交互作用下串补振荡模式的阻尼会明显降低，并且在模式交互作用强弱变化过程中弱阻尼或负阻尼次同步振荡模式的频率会发生漂移。
3）在混合风电场中，DFIG EMO模式会随着风速变化依次与不同的其他风电机组的控制模式发生强交互作用，引发不同频段的次同步功率振荡。
4）随着D-PMSG输出有功功率的增加，D-PMSG直流电压外环主导振荡模式的留数会增大，使得该模式与其他控制模式的交互作用程度会加剧，从而导致弱阻尼或负阻尼的次同步振荡模式以及频率的漂移。
风速和并网风机数量决定了风电场动态特性的时变性，本文研究的是风速这一因素引发的开环模式耦合。类比本文结论，并网风机数量的变化也可能存在类似现象，这将有可能拓展现有文献关于并网风机数量引发频率漂移的结论。下一步的研究方向是次同步振荡频率漂移的控制方法，基于本文的研究结论，以消除开环模式耦合条件、减弱模式间的相互作用程度为目的，通过重新配置换流器控制参数或者附加阻尼控制器，保证并网风电机组在多风速下的安全稳定运行。
附 录
1. 式（6）特征根求解过程
式（6）特征方程可表示为
进一步展开可得
式中， 
根据式（A2），可知
1）当不考虑RSC电流内环控制时，特征方程为
由此，得到式（7）。
2）当考虑RSC电流内环控制时，特征方程为
由式（A4）可解得
根据式（A5）可知，特征方程的根与转子转速有关。并且，由于积分环节的主要作用是消除实际值和参考值之间的静态误差，积分系数的取值并不大[23]，因此在式（A5）中，K相对于M的实部而言较小，在忽略K的作用时，可得到式（8）的结果。
2. 开环模式耦合条件下的开、闭环振荡模式的关系
通常由于风电机组换流器控制的快速调节特性，风电场与外部电力系统的动态交互较弱，风电场输出电流的扰动值很小，亦即
以一个小的正实数ε（01ε＜≪）来表征这种弱交互的特性，则有
两个子系统为双输入双输出结构，互联模型的特征方程为
结合式（A6）和式（A7），可得
不失一般性，记
结合式（A8）和式（A9）可得
将式（A10）展开可得
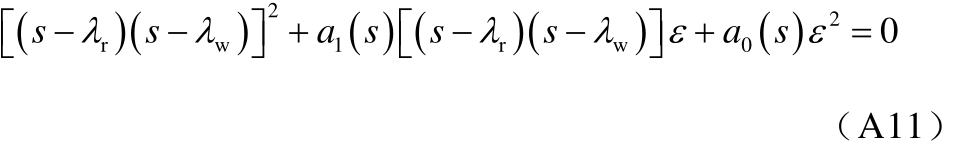
式中
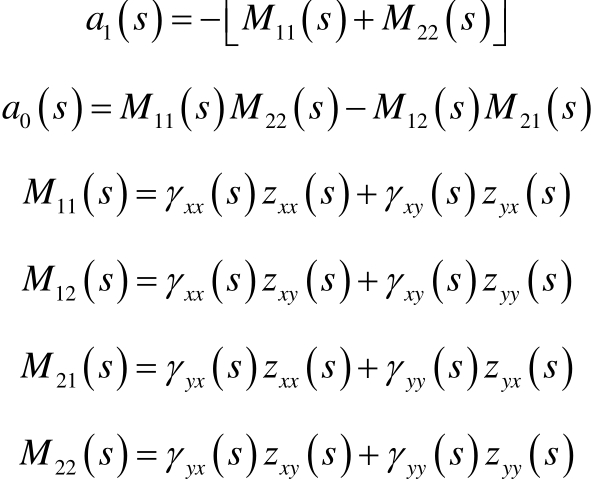
开环振荡模式λr和λw所对应的闭环振荡模式
和
为式（A11）的解。在开环模式耦合条件 λr≈λw下可得
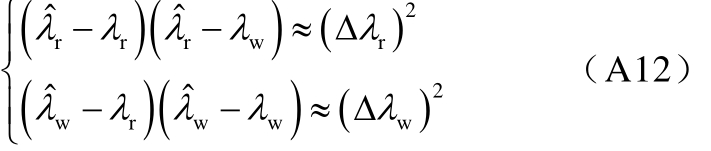
由于01ε＜≪，忽略式（A11）中包含ε的高阶项，则有
结合式（A12）和式（A13）可得
根据式（A7）~式（A11）可得
将式（19）代入到式（A15）中，可得
亦即
3. 仿真模型参数
附表1 DFIG参数
App.Tab.1 Parameters of DFIG
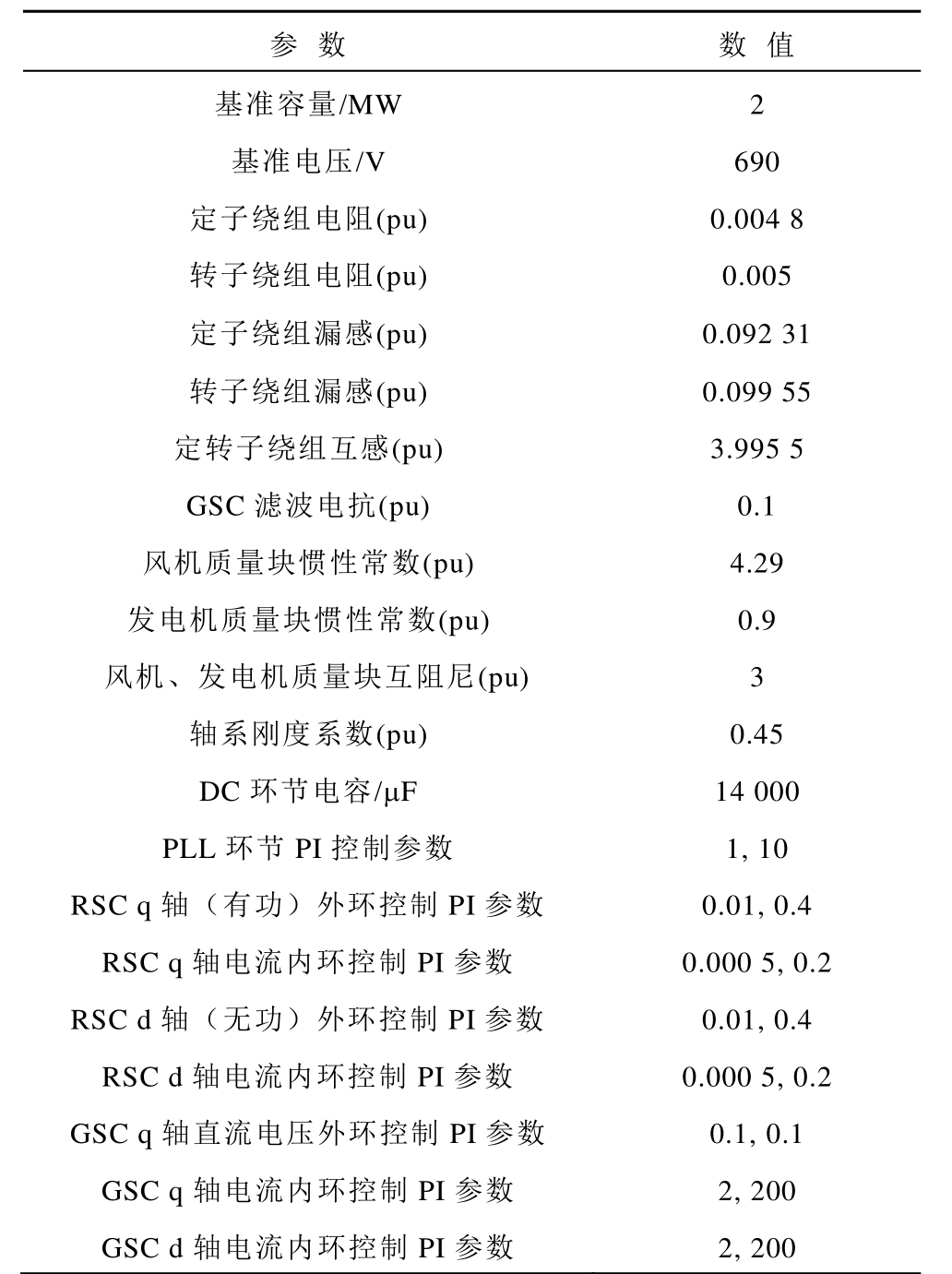
参 数 数 值基准容量/MW 2基准电压/V 690定子绕组电阻(pu) 0.004 8转子绕组电阻(pu) 0.005定子绕组漏感(pu) 0.092 31转子绕组漏感(pu) 0.099 55定转子绕组互感(pu) 3.995 5 GSC滤波电抗(pu) 0.1风机质量块惯性常数(pu) 4.29发电机质量块惯性常数(pu) 0.9风机、发电机质量块互阻尼(pu) 3轴系刚度系数(pu) 0.45 DC环节电容/μF 14 000 PLL环节PI控制参数 1, 10 RSC q轴（有功）外环控制PI参数 0.01, 0.4 RSC q轴电流内环控制PI参数 0.000 5, 0.2 RSC d轴（无功）外环控制PI参数 0.01, 0.4 RSC d轴电流内环控制PI参数 0.000 5, 0.2 GSC q轴直流电压外环控制PI参数 0.1, 0.1 GSC q轴电流内环控制PI参数 2, 200 GSC d轴电流内环控制PI参数 2, 200
附表2 D-PMSG参数
App.Tab.2 Parameters of D-PMSG
参 数 数 值基准容量/MW 2基准电压/V 690定子绕组电阻(pu) 0.002 5定子绕组漏感(pu) 0.02定转子绕组d轴互感(pu) 0.43定转子绕组q轴互感(pu) 0.48 DC 电容/ μF 60 000滤波电抗(pu) 0.1转子惯性常数(pu) 8 PLL环节PI控制参数 0.1, 2 MSC q轴电磁转矩外环控制PI参数 5, 20 MSC q轴电流内环控制PI参数 1, 100 MSC d轴电流内环控制PI参数 1, 100 GSC d轴直流电压外环控制PI参数 0.06, 15和0.13, 50 GSC d轴电流内环控制PI参数 0.01, 10 GSC q轴无功外环控制PI参数 0.25, 5 GSC q轴电流内环控制PI参数 0.01, 10
附表3 输电线路参数
App.Tab.3 Parameters of transmission line
参 数 数 值X1(pu) 0.01 X2(pu) 0.01 X3(pu) 0.01 RL(pu) 0.02 XL(pu) 0.15
[1] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[2] Wang Liang, Xie Xiaorong, Jiang Qirong, et al.Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system[J]. IEEE Transactions on Power Systems, 2015,30(5): 2772-2779.
[3] Liu Huakun, Xie Xiaorong, Zhang Chuanyu, et al.Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model[J]. IEEE Transactions on Power Systems, 2016,32(1): 474-483.
[4] Xie Xiaorong, Zhang Xu, Liu Huakun, et al.Characteristic analysis of subsynchronous resonance in practical wind farms connected to seriescompensated transmissions[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1117-1126.
[5] Mohammadpour H A, Santi E. Modeling and control of gate-controlled series capacitor interfaced with a DFIG-based wind farm[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 1022-1033.
[6] Fan Lingling, Zhu Chanxia, Miao Zhixin, et al. Modal analysis of a DFIG-based wind farm Interfaced with a series compensated network[J]. IEEE Transactions on Energy Conversion, 2011, 26(4): 1010-1020.
[7] 边晓燕, 施磊, 宗秀红, 等. 多运行方式下风电机组变频器参与次同步相互作用的分析与抑制[J].电工技术学报, 2017, 32(11): 38-47.Bian Xiaoyan, Shi Lei, Zong Xiuhong, et al. Analysis and mitigation of wind turbine converters in subsynchronous interaction under multi-operation conditions[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 38-47.
[8] 陈斐泓, 杨健维, 廖凯, 等. 基于频率扫描的双馈风电机组次同步控制相互作用分析[J].电力系统保护与控制, 2017, 45(24): 84-91.Chen Feihong, Yang Jianwei, Liao Kai, et al. Subsynchronous control interaction analysis in doubly-fed induction generator based on frequency scanning[J].Power System Protection and Control, 2017, 45(24):84-91.
[9] Miao Zhixin. Impedance-model-based SSR analysis for type 3 wind generator and series-compensated network[J]. IEEE Transactions on Energy Conversion,2012, 27(4): 984-991.
[10] 赵书强, 李忍, 高本锋, 等. 适用于多源系统次同步振荡分析的图形化建模方法[J]. 电工技术学报,2017, 32(14): 184-193.Zhao Shuqiang, Li Ren, Gao Benfeng, et al. A graphical modeling method applied for multi-sources system subsynchronous oscillation analysis[J].Transactions of China Electrotechnical Society, 2017,32(14): 184-193.
[11] Liu Huakun, Xie Xiaorong, He Jingbo, et al.Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J].IEEE Transactions on Power Systems, 2017, 32(6):4708-4720.
[12] 宋瑞华, 郭剑波, 李柏青, 等. 基于输入导纳的直驱风电次同步振荡机理与特性分析[J]. 中国电机工程学报, 2017, 37(16): 4662-4670.Song Ruihua, Guo Jianbo, Li Baiqing, et al.Mechanism and characteristics of subsynchronous oscillation in direct-drive wind power generation system based on input-admittance analysis[J].Proceedings of the CSEE, 2017, 37(16): 4662-4670.
[13] 谢小荣, 刘华坤, 贺静波, 等. 直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366-2372.Xie Xiaorong, Liu Huakun, He Jingbo, et al.Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems[J].Proceedings of the CSEE, 2016, 36(9): 2366-2372.
[14] 任必兴, 杜文娟, 王海风. STATCOM 与 PMSG的次同步控制交互研究[J]. 电工技术学报, 2018,33(24): 5884-5896.Ren Bixing, Du Wenjuan, Wang Haifeng. Study on sub-synchronous control interaction between STATCOM and PMSG[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5884-5896.
[15] Du Wenjuan, Chen Chen, Wang Haifeng. Subsynchronous interactions induced by DFIGs in power systems without series compensated lines[J]. IEEE Transactions on Sustainable Energy, 2018, 9(3): 1275-1284.
[16] 王旭斌, 杜文娟, 王海风. 开环模式谐振引发含变速风电机组电力系统振荡的机理分析[J]. 中国电机工程学报, 2017, 37(22): 6481-6491.Wang Xubin, Du Wenjuan, Wang Haifeng.Oscillations caused by open-loop modal resonance in power system with variable-speed wind generator[J].Proceedings of the CSEE, 2017, 37(22): 6481-6491.
[17] Du Wenjuan, Wang Yang, Wang Haifeng, et al.Concept of modal repulsion for examining the subsynchronous oscillations in power systems[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4614-4624.
[18] 贺益康, 胡家兵, 徐烈. 并网双馈异步风力发电机运行控制[M]. 北京: 中国电力出版社, 2012.
[19] Porter B, Crossley R, Lpscutoff W V. Modal control:theory and applications[M]. London: Taylor and Francis, 1972.
[20] Fan Lingling, Kavasseri R, Miao Z L, et al. Modeling of DFIG-based wind farms for SSR analysis[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2073-2082.
[21] 陈宝平, 林涛, 陈汝斯, 等. 直驱风电场经 VSCHVDC并网系统的多频段振荡特性分析[J]. 电工技术学报, 2018, 33(增刊1): 176-184.Chen Baoping, Lin Tao, Chen Rusi, et al.Characteristics of multi-band oscillation for direct drive wind farm interfaced with VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 176-184.
[22] Li Shuhui, Haskew T A, Swatloski R P, et al. Optimal and direct-current vector control of direct-driven PMSG wind turbines[J]. IEEE Transactions on Power Electronics, 2012, 27(5): 2325-2337.
[23] Harnefors L, Bongiorno M, Lundberg S. Inputadmittance calculation and shaping for controlled voltage-source converters[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3323-3334.