0 引言
无线电能传输(Wireless Power Transfer, WPT)技术借助磁场、电场、激光、微波等软介质实现电能从电源系统到用电设备的无电气接触传输[1-3],具有便捷、灵活、安全、可靠等优点[4-6],已成为国内外科研机构研究与开发的热点[7-9]。其中,基于电场耦合的电能传输(Electric-Field Coupled Power Transfer, ECPT)方式具有以下特点:电能耦合机构简易轻薄、成本低且形状易变[10-11];在工作状态中,电场耦合机构的绝大部分电通量分布于电极之间,对周围环境的电磁干扰很小[12-13];当电场耦合机构之间或周围存在金属导体时,不会引起导体产生涡流损耗等[14-15]。在某些领域的应用可与基于磁场耦合的无线电能传输技术形成优势互补,因此越来越多的专家学者围绕ETCP技术展开研究[16-20]。
在某些ECPT技术的应用场景中,例如电动汽车、厨房电器以及消费电子等可移动负载设备的充/供电[10-11,14],系统的电能拾取端(负载、拾取端耦合极板以及功率调节电路等)经常会从供电系统中移入/移除。拾取端的移入/移除可视为一个机械过程,其时间尺度远大于ECPT系统的运行周期。另一方面,在实际应用中,许多用电设备都安装电源开关,开关的通断可等效为用电设备负载的投入/切除。例如电热水壶,当水沸腾后会自动切断电源。上述工况可视为负载在极短的时间内投入到系统或从系统中切除。为了便于区分,本文将拾取端的移入/移除称为负载的移入/移除,将用电设备的投入/切除称为负载的投入/切除。此外,在实际应用中有很多用电设备要求供电系统对一定范围内的负载变化具有恒压输出特性[13]。
现有文献只是针对上述需求的某一方面展开了研究,如文献[16]针对恒压输出的需求提出了一种基于T-Π复合谐振网络的ECPT系统,但是其拾取端的电路结构比较复杂。当拾取端切除时,其采用的串联补偿方式易在补偿电感上产生很大的电压尖峰并且流经开关管的电流也会发生过冲。文献[14]提出一种基于Z阻抗补偿的ECPT系统,有效地解决了负载投入/切除过程中补偿电感的电压尖峰问题。然而,该ECPT系统的逆变输出电流在负载切除后激增,存在烧毁逆变器开关管的风险,系统的空载功耗很大(文献[11,17]中的 ECPT系统在负载切除后的功耗也很大)。文献[15]研究了基于E类变换器的ECPT系统负载软切换问题,为了使系统在负载切除后工作于低功耗待机状态,引入 Buck变换器调节系统的输入功率,增加了系统成本和电路复杂度。此外,文献[14-15]中的ECPT系统均不具备恒压输出特性。
本文针对ECPT系统的负载自适应问题及如何保证系统负载在一定范围变化下具有恒压输出特性问题展开研究。由于 WPT系统的负载自适应问题有其特殊性,因此本文提出了“WPT系统的负载自适应”概念,其定义为:WPT系统的负载在任意时刻的移入/移除和投入/切除都不会对逆变器开关管造成明显的电压电流过冲。当负载移入/投入后,系统能够高效稳定地为负载提供需要的功率;当负载移除/切除后,系统能够自动进入低功耗待机状态。为满足负载自适应且同时具备恒压输出特性的要求,本文基于 T型 CLC谐振网络提出了一种具有负载自适应特性的恒压型ECPT系统,并给出了系统参数设计方法。无论负载是移入/移除还是投入/切除,该系统都能防止逆变器开关管出现过电压和过电流冲击。在负载移除/切除后,系统自动进入低功耗待机状态;在负载移入/投入后,系统能够重新高效地为负载传输功率,并且能够确保负载在一定范围内变化时,系统具有较好的恒压输出特性。以上所有功能都是通过系统拓扑及其参数设计方法实现的,不依赖任何额外的检测和控制电路,降低了系统成本和控制器的设计难度。
1 具有恒压输出特性的ECPT系统
1.1 系统结构及工作原理
图1为本文提出的ECPT系统拓扑。其中,供电电源Edc、全桥型逆变器(S1~S4组成)、谐振电感L1~L3、谐振电容 C1、C2与两块发射极板共同构成系统的电能发射端。全桥整流器(VD1~VD4)、滤波电容 Cf、负载电阻 RL与两块接收极板构成系统的电能拾取端。

图1 本文提出的ECPT系统拓扑
Fig.1 The ECPT system topology proposed in this paper
该系统的直流输入经过全桥变换器和发射端谐振网络后得到高频交流电,在其作用下,耦合机构的两对极板之间形成交互电场,在交互电场的作用下产生位移电流“流过”极板,实现电能的无线传输。
图2为ECPT系统的等效电路。其中,全桥逆变器的输出等效为一个方波电压源uin,CS表示电场耦合机构的等效电容,CS=CS1CS2/(CS1+CS2);Req表示负载电阻RL与全桥整流器的等效电阻,Req=8RL/π2[14]。图 1中的谐振电容 C1和C2分别表示C1a、C1b的串联和C2a、C2b的串联。整个ECPT系统的谐振网络可看作由N1、N2和N3三个子网络组成,N2和N3网络即为T型CLC谐振网络。需要说明的是,本文中ECPT系统的特性分析及其参数设计方法均是基于T型CLC谐振网络展开的。
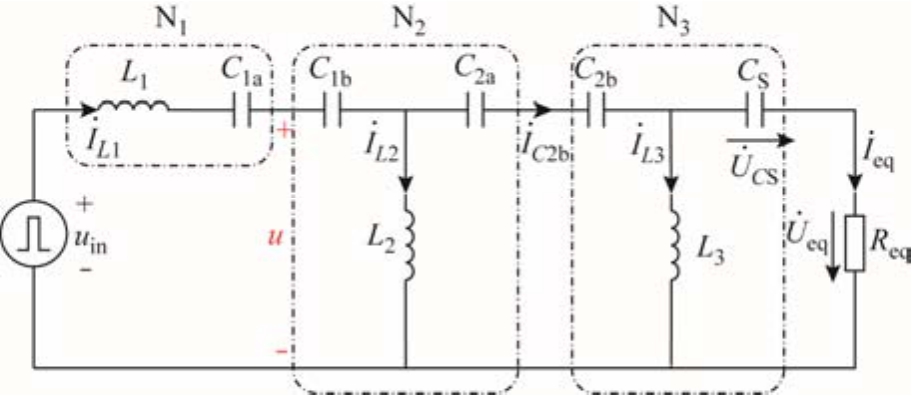
图2 ECPT系统的等效电路
Fig.2 Equivalent circuit of the ECPT system
1.2 T型CLC谐振网络分析
图3 为T型CLC谐振网络的电路,假设输入为理想的交流电压源 1U˙。
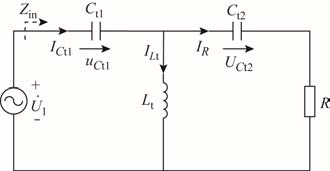
图3 T型CLC谐振网络
Fig.3 T-CLC resonant network
忽略电路中无功元件的损耗,可以得到
式中,Zin、ω0、ωn、Q和λ分别为T型CLC网络的输入阻抗、谐振角频率、归一化角频率、负载品质因数和电容比,且

式中,ω为T型CLC网络的工作角频率。输出电流为
负载电流相对于输入电流的增益可表示为
T型 CLC网络的特性取决于归一化角频率 ωn与电容比λ的不同组合。当ωn=1时,联立式(1)、式(3)和式(4)可得

当λ=1时,式(5)可简化为

由式(6)可知,当ωn=1,λ=1时,T型 CLC网络运行在零相角输入状态,功率因数较高。此外,T型CLC网络的输入阻抗与负载电阻呈反比的关系,可根据负载电阻的大小将输入阻抗放大或者缩小。
1.3 ECPT系统恒压输出特性分析
结合图 2和图 3,当 N2和 N3网络中的电感电容参数满足上述T型CLC谐振网络的参数关系时,根据式(2)和式(6)可得
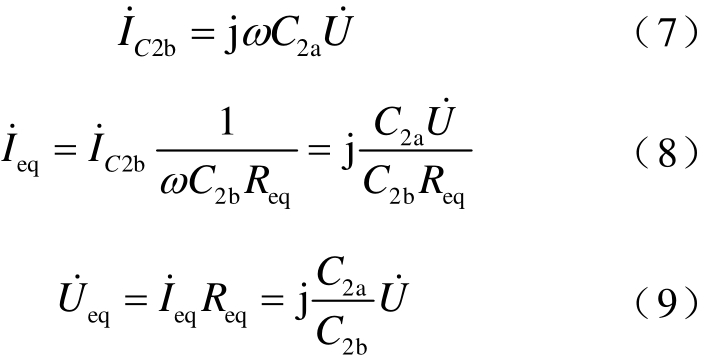
式中,U˙为电压u的相量形式。使用傅里叶三角级数公式将逆变输出电压展开,即

式中,Edc为供电电压的幅值。由L1、C1a构成的串联LC网络N1作为输入滤波器,能够有效抑制高次谐波注入到后级谐振网络,提高系统的电能传输效率[14]。N1网络的电感电容参数需满足
进而可以得到
式中,ufd为逆变输出电压的基波分量。令C2a=kC2b,则式(9)可表示为
根据式(12)和式(13)可以得到在忽略电路元件内阻及基波近似成立时,本文提出的ECPT系统输出电压与负载电阻无关,具有恒压输出特性。
2 系统负载自适应特性分析
在第1节提出的 ECPT系统等效电路基础上,结合 T型 CLC谐振网络的特性推导出该系统具备恒压输出特性。本节将基于 T型 CLC谐振网络进一步分析系统的负载自适应特性,为简化稳态时的分析,采用基波近似的方法建立系统的模型。
2.1 系统满载时的稳态等效电路
系统满载工作时的等效电路如图2所示,根据式(6)可将图2中的T型CLC谐振网络N3和Req简化为Zeq,得到如图4所示的等效电路,其中

图4 系统满载时的等效电路
Fig.4 Equivalent circuit of the ECPT system with load
图4 中包含T型CLC谐振网络N2,根据式(6)和前述分析,可将图4进一步简化为图5所示的等效电路。如图5所示,当k>1时,等效负载电阻缩小了k2倍,有利于提升系统的功率传输能力。

图5 系统满载简化后的等效电路
Fig.5 The simplified circuit of the system with load
2.2 系统空载时的稳态等效电路
根据图1所示的系统拓扑可知,负载移除(即拾取端移除)和切除后系统的等效电路基本一致,可用图6统一表示。

图6 负载移除后系统的等效电路
Fig.6 The equivalent circuit of the ECPT system with no load
由于图 2中的 Req=8RL/π2,图 5中的等效负载电阻为(1/k)2Req,因此当负载移除/切除后,图 6所示的ECPT系统等效电路从输入端看过去等效为开路。根据电路基本理论可知,这样的电路特性可以达到抑制负载移除/切除过程中逆变器开关管电流电压过冲的效果。
综上所述,当负载投入后,本文提出的ECPT系统可等效为一个正弦电压源串联一个阻值为(1/k)2Req的电阻;当负载移除/切除后,系统等效为开路。因而,本文提出的ECPT系统无需任何额外的检测和控制电路即可实现当负载投入后,为负载传输电能;当负载切除后,工作在低功耗待机状态。
3 系统参数设计方法
需要注意的是,前文所有的公式推导均是基于基波近似的方法,因而系统模型和分析的准确性取决于输入电流 iL1的总谐波畸变率(Total Harmonic Distortion, THD)。THD可用来判断逆变输出电流波形是否为标准的正弦波。本文中,THD定义为

式中,I1和In分别为输入电流iL1的基波分量和奇次谐波分量的有效值。
根据式(13)和Req的表达式,可得系统输出功率Pout的表达式为
综合上述分析,本文提出的ECPT系统参数设计方法的流程如图7所示。通常根据负载要求设定RL的值,根据输出功率要求设定 Edc和 k的初值,根据使用场所的空间限制设定 CS的初值,根据工程经验设定f的初值。需要说明的是,根据式(16)可知,当 k>1时有利于提升系统的输出功率,但是k值的增加使得系统等效负载电阻减小,其他部分损耗的占比增大,导致系统的电能传输效率降低。因此本文在仿真和实验研究的基础上确定 k的取值范围为1<k<3;由于式(16)是在忽略电路元件内阻的条件下得到的,考虑到实际电路元件损耗的存在,应在输出功率Pout之前乘以一个裕量系数a,a通常取110%~120%;目前绝大多数ECPT系统的工作频率都在2MHz以内,系统中单个谐振电感值大都在300μH以内[11-20],因此取频率f<2MHz,电感 L<300μH,L表示任意谐振电感。然后按照图 7 所示的参数设计流程确定 L1、L2、L3、C1、C2、f和 CS的值。
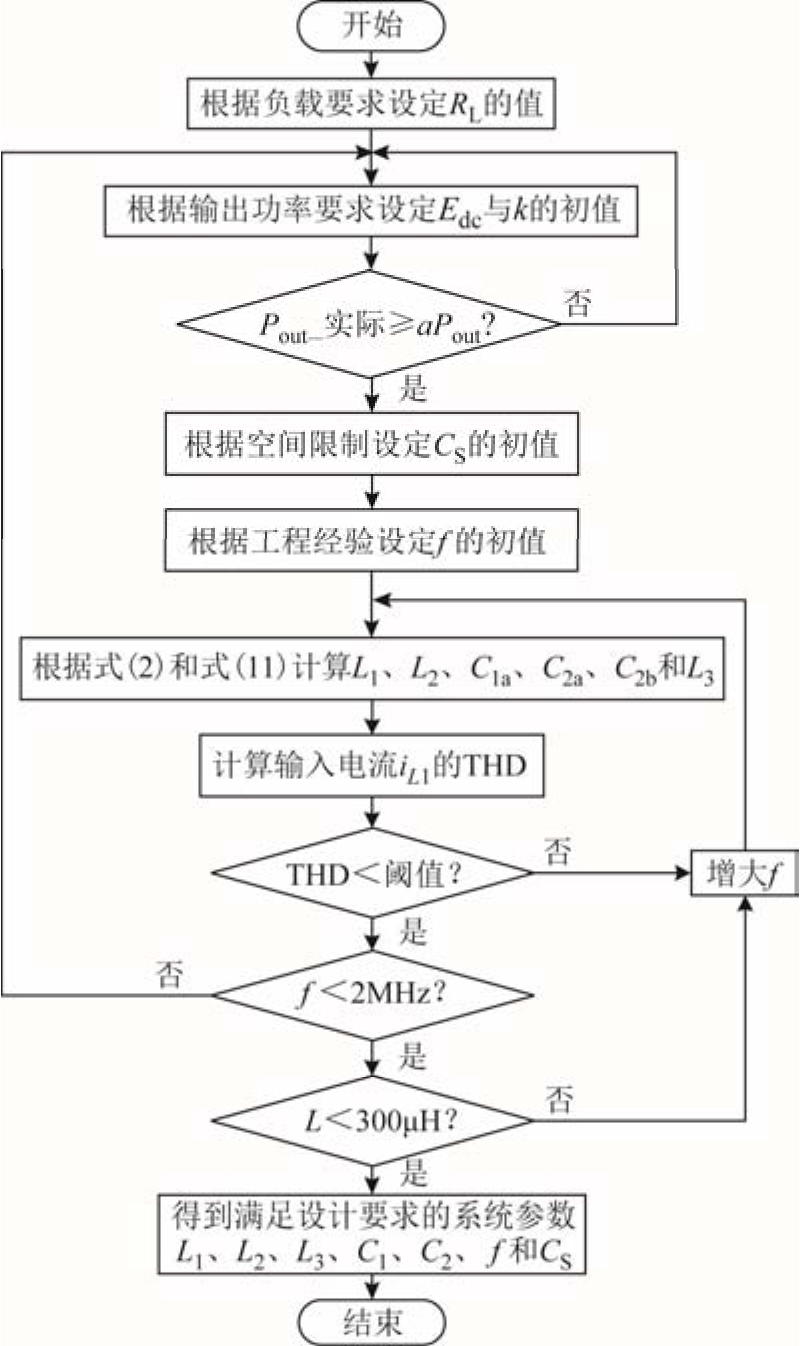
图7 系统主要参数设计流程
Fig.7 The flow chart of the system parameter design
当输入电流iL1的THD和谐振电感不满足判断条件时,可适当增大系统的运行频率f。这是因为增大系统的运行频率 f有利于减小谐振电感的体积,提升系统的品质因数。当运行频率 f不满足判断条件时,通常只能重新设置Edc、k和CS等初始参数,然后按照参数设计流程重新计算。
4 仿真与实验验证
为了验证本文提出的ECPT系统拓扑及其参数设计方法的可行性及有效性,根据图1所示的ECPT系统拓扑在 Matlab仿真平台建立了系统的仿真电路模型。首先设定RL的值和 Edc、k、f、CS的初值,然后按照图7所示的参数设计流程确定L1、L2、L3、C1、C2、f、CS的值,得到系统主要参数值见表 1,将此参数代入仿真模型,通过仿真得到图 8~图 10所示的结果。
表1 系统主要参数
Tab.1 Main parameters of the system

参 数 数 值 参 数 数 值Edc/V 28 L2/μH 101.32 RL/Ω 70 L3/μH 202.64 CS/pF 500 C1/pF 666.6 f /kHz 500 C2/pF 333.3 L1/μH 50.66
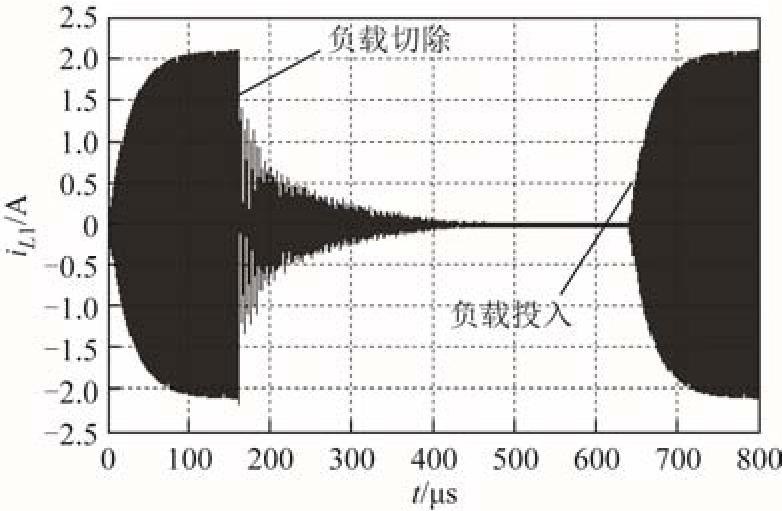
图8 负载切除/投入时逆变输出电流仿真波形
Fig.8 Simulated transient response of the inverter output current when the load is switched off and on
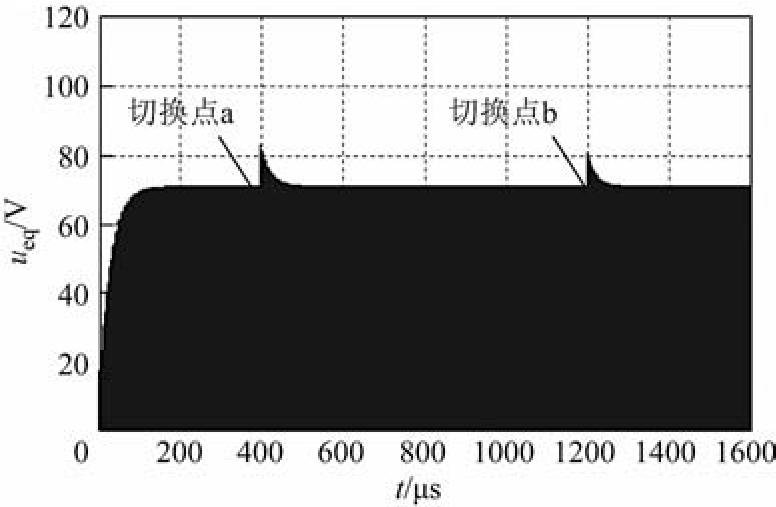
图9 负载电阻切换时(增大)系统的输出电压波形
Fig.9 The output voltage waveform of the system when switch the load resistor (increase)
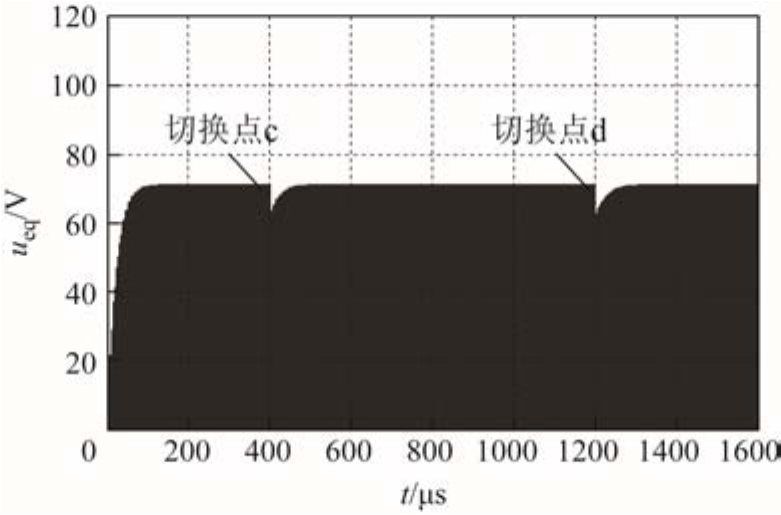
图10 负载电阻切换时(减小)系统的输出电压波形
Fig.10 The output voltage waveforms of the system when switch the load resistor (decrease)
图8 为负载切除/投入时逆变输出电流的瞬态响应仿真波形。当负载切除后,逆变输出电流没有出现任何尖峰并快速减小到0.02A以下,系统处于低功耗待机状态;当负载投入后,逆变输出电流迅速增大到系统满载工作时的电流值。由于逆变器为电压型全桥谐振变换器,由S1~S4共四个MOSFET构成逆变网络,两组开关(S1、S4)与(S2、S3)以互补导通的方式产生方波逆变输出电压。当其中一组开关导通时,另一组开关的两个开关管的端电压均等于供电电压,因此在负载投切的过程中不会对逆变器开关管产生过电压冲击。
图 9为负载电阻从 60Ω切换到 70Ω再切换至80Ω时系统的输出电压波形。图 10为负载电阻从80Ω切换到 70Ω再切换至 60Ω时系统的输出电压波形。由图9和图10可知,在负载切换的过程中,系统的输出电压保持恒定,表明本文提出的 ECPT系统具有恒压输出特性,与前述理论分析一致。
图11是基于文献[14]中的ECPT系统及其参数得到的负载切除时逆变输出电流瞬态响应仿真波形。由图可知,负载切除后逆变输出电流激增,存在烧毁逆变器开关管的风险,同时表明该ECPT系统的空载功耗很大。与文献[14]中的ECPT系统相比,本文提出的ECPT系统及其参数设计方法能够显著降低负载切除后系统的功耗。

图11 负载切除时逆变器输出电流瞬态响应仿真波形
Fig.11 Simulated transient response of the inverter output current when the load is switched off
本文在理论分析和仿真研究的基础上,根据图1所示的系统拓扑和表1中的系统参数搭建了如图12所示的实验装置,进一步验证系统的负载自适应特性和恒压输出特性。
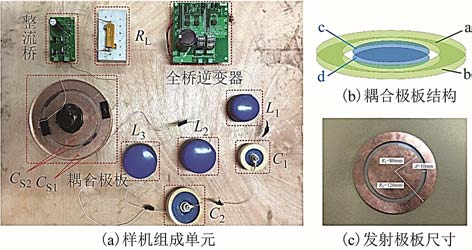
图12 实验装置
Fig.12 Experimental prototype
图12 a中的实验装置包括全桥逆变器、L1、L2、L3、C1与 C2组成的谐振网络、耦合极板CS1和 CS2、整流桥与负载电阻;图12b为耦合极板的结构图,a与 b构成了 CS1,c与 d构成了 CS2;发射极板的尺寸如图12c所示(接收极板与发射极板相同),发射极板与接收极板的间距约为1mm。全桥逆变器采用的 MOSFET的型号为 STP30NF20,整流二极管的型号为HFA08TB60,谐振电感为李兹线绕制的空心电感,谐振电容为陶瓷电容。
图13为负载切除时逆变输出电流电压的瞬态响应实验波形。图14为负载投入时逆变输出电流电压的瞬态响应实验波形。需要说明的是,在负载切除后,图8中的逆变输出电流有明显的衰减过程,而图13中则不能直观地看出这一过程,这是因为图8(μs级)与图 13(s级)的时间尺度不一致造成的。总的来说,负载投切的实验波形与仿真波形的一致性较好。
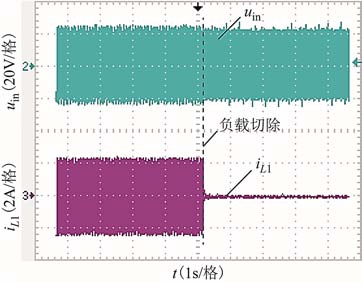
图13 负载切除时逆变器输出电流电压瞬态响应实验波形
Fig.13 Experimental transient response of the inverter output voltage and current when the load is switched off

图14 负载投入时逆变器输出电流电压瞬态响应实验波形
Fig.14 Experimental transient response of the inverter output voltage and current when the load is switched in
系统满载(70Ω)时的直流输入电压为28V,输入电流为1.6A。负载两端的直流电压为51V,系统的输出功率为37W,系统的电能传输效率约为83%;当负载切除后,系统的输入功率小于0.2W。本文搭建的 ECPT系统实验装置的满载效率与文献[11,14,17]中的ECPT系统的传输效率基本相当,即与目前的研究水平相当。空载时的系统功耗远低于这些ECPT系统,因此本系统的应用能带来很好的节能效果。由图13、图14及第3节的理论分析可知,本文提出的ECPT系统无需任何额外的检测和控制电路即可实现在负载投入后,高效稳定地为负载传输功率;在负载切除后工作在低功耗待机状态。在负载投入/切除的过程中,逆变器开关管没有出现任何的电流电压冲击。因此,本文提出的ECPT系统具备负载自适应特性。

图15 负载电阻切换时系统的输出电压波形
Fig.15 The output voltage waveform of the system with the load variation
图15 为负载电阻从80Ω切换到70Ω再切换至80Ω时系统的输出电压波形。由图可知,系统的输出电压经历了从53V变为51V再变为53V的过程,系统的输出电压基本保持恒定。
图 16为根据实验测试数据得到的输出电压随负载电阻的变化曲线。在表1所示的系统参数下,当负载电阻在 50~100Ω变化时,负载变化率约为30%~40%,在该负载变化率下,系统输出电压的变化范围在设计值(51V)±3V以内,输出电压变化率约为6%,能满足大多数实际工程的要求。

图16 输出电压随负载电阻的变化曲线
Fig.16 The curve of output voltage with load resistance
图 17为根据实验测试数据得到的系统功效特性曲线(根据表1中的参数可知k=2)。系统损耗主要来源于逆变器开关管损耗、谐振网络损耗以及整流二极管损耗。由系统满载输入功率和输出功率可推出系统损耗为 7.8W。逆变器开关管损耗约为0.8W,占总损耗的10.26%;整流二极管的损耗约为3.9W,占总损耗的50%;谐振网络的损耗约为3.1W,占总损耗的39.74%。由图17可知,随着负载电阻的增大,系统的电能传输效率逐渐升高。负载电阻越小,系统的电能传输效率越低,这也验证了k值的增加会使得系统等效负载电阻减小,系统损耗增大,导致系统的电能传输效率降低。

图17 系统功效特性曲线(k=2)
Fig.17 The curve of system energy efficiency characteristics
由图16和图17可知,由于实际电路元件损耗的存在,当负载电阻较小时(特别是小于额定电阻时),系统的电能传输效率较低,输出电压与设计值偏差较大,因此图 16中当负载电阻的变化范围为10~100Ω时,输出电压的变化范围较大。随着负载电阻增大,系统效率升高且逐渐稳定,系统的输出电压变化率在逐渐变小,恒压效果逐渐变好,输出电压趋于稳定。因此,本文提出的ECPT系统只能对一定范围内的负载变化具有恒压输出特性。
5 结论
本文基于 T型 CLC谐振网络提出了一种具有负载自适应特性的恒压型ECPT系统,并给出了系统参数设计方法。仿真和实验结果验证了本文提出的ECPT系统及其参数设计方法的可行性和有效性。所搭建的ECPT实验样机无需任何额外的检测和控制即可实现在负载投入后,传输超过35W的功率,效率达到80%以上,在负载切除后工作于低功耗待机状态。本文提出的ECPT系统及其参数设计方法具有以下几点优势:
1)在负载移入/移除和投入/切除的过程中,不会出现任何的电压电流冲击。
2)无需任何额外的检测和控制电路,系统在负载切除后自动运行在低功耗待机状态。
3)谐振补偿网络在电源与负载之间提供了阻抗匹配功能,有利于提升系统的功率传输能力。
4)系统的输出电压对一定范围内的负载变化具有恒压输出特性。
5)系统拾取端没有无功补偿元件,有利于提高拾取端的功率密度,便于应用推广。
在后续工作中,将对k值的理论取值依据及耦合机构等效电容 CS变化下系统的恒压输出特性展开研究。
[1] 杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J]. 电工技术学报,2015, 30(5): 1-8.Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al.Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J].Transactions of China Electrotechnical Society, 2015,30(5): 1-8.
[2] 张波, 疏许健, 黄润鸿. 感应和谐振无线电能传输技术的发展[J]. 电工技术学报, 2017, 32(18): 3-17.Zhang Bo, Shu Xujian, Huang Runhong. The development of inductive and resonant wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 3-17.
[3] 黄学良, 谭林林, 陈中, 等. 无线电能传输技术研究与应用综述[J]. 电工技术学报, 2013, 28(10): 1-11.Huang Xueliang, Tan Linlin, Chen Zhong, et al.Review and research progress on wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 1-11.
[4] 毛世通, 朱春波, 宋凯, 等. 基于端口阻抗的磁耦合谐振式无线电能传输特征参数仿真方法研究[J].电工技术学报, 2015, 30(19): 95-102.Mao Shitong, Zhu Chunbo, Song Kai, et al.Characteristic parameter simulation method for magnetic coupling resonance wireless power transfer based on port impedance[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 95-102.
[5] 麦瑞坤, 陆立文, 李勇. 两逆变器并联的 IPT系统的环流消除方法研究[J]. 电工技术学报, 2016,31(3): 8-15.Mai Ruikun, Lu Liwen, Li Yong. Circulating current elimination of parallel dual-inverter for IPT system[J].Transactions of China Electrotechnical Society, 2016,31(3): 8-15.
[6] 夏晨阳, 李玉华, 雷轲, 等. 变负载ICPT系统电能与信号反向同步传输方法[J]. 中国电机工程学报,2017, 37(6): 1857-1866.Xia Chenyang, Li Yuhua, Lei Ke, et al. Study on power forward and signal reverse transmission in load changing ICPT system[J]. Proceedings of the CSEE,2017, 37(6): 1857-1866.
[7] 胡宏晟, 蔡涛, 段善旭, 等. 用于WPT系统的一次侧失谐 SS型补偿拓扑及其参数设计方法[J]. 电工技术学报, 2017, 32(18): 73-82.Hu Hongsheng, Cai Tao, Duan Shanxu, et al. Study of the primary side detuned series-series compensated topology and parameter design for WPT system[J].Transactions of China Electrotechnical Society, 2017,32(18): 73-82.
[8] Tang Yunyu, Chen Yi, Madawala U K, et al. A new controller for bidirectional wireless power transfer systems[J]. IEEE Transactions on Power Electronics,2018, 33(10): 9076-9087.
[9] Xu Ligang, Chen Qianhong, Ren Xiaoyong, et al. Selfoscillating resonant converter with contactless power transfer and integrated current sensing transformer[J].IEEE Transactions on Power Electronics, 2017, 32(6):4839-4851.
[10] Lu Fei, Zhang Hua, Mi C C. A review on the recent development of capacitive wireless power transfer technology[J]. Energies, 2017, 10(1): 1-30.
[11] Lu Fei, Zhang Hua, Hofmann H, et al. A double-sided LCLC-compensated capacitive power transfer system for electric vehicle charging[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6011-6014.
[12] 苏玉刚, 谢诗云, 呼爱国, 等. LCL复合谐振型电场耦合式无线电能传输系统传输特性分析[J]. 电工技术学报, 2015, 30(19): 55-60.Su Yugang, Xie Shiyun, Hu Aiguo, et al. Transmission property analysis of electric-field coupled wireless power transfer system with LCL resonant network[J].Transactions of China Electrotechnical Society, 2015,30(19): 55-60.
[13] Su Yugang, Xie Shiyun, Hu A P, et al. Capacitive power transfer system with a mixed-resonant topology for constant-current multiple-pickup applications[J].IEEE Transactions on Power Electronics, 2017,32(11): 8778-8786.
[14] Huang Liang, Hu A P, Swain A, et al. Z-impedance compensation for wireless power transfer based on electric field[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7556-7563.
[15] 苏玉刚, 赵鱼名, 谢诗云, 等. 电场耦合无线电能传输系统负载软切换控制技术[J]. 电工技术学报,2017, 32(18): 44-51.Su Yugang, Zhao Yuming, Xie Shiyun, et al. Control of load soft-switched for electric-field coupled power transfer system[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 44-51.
[16] 苏玉刚, 谢诗云, 唐春森, 等. 基于 T-Π 复合谐振网络的恒压型电场耦合无线电能传输系统[J]. 电工技术学报, 2018, 33(8): 1685-1695.Su Yugang, Xie Shiyun, Tang Chunsen, et al. An electric-field coupled power transfer system with constant voltage output based on T-Π mixed resonant circuit[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1685-1695.
[17] Theodoridis M P. Effective capacitive power transfer[J]. IEEE Transactions on Power Electronics,2012, 27(12): 4906-4913.
[18] 陈希有, 陈建辉, 牟宪民, 等. 空间电场耦合单线电力传输:仿真、理解与构建[J]. 中国电机工程学报, 2017, 37(19): 5749-5758.Chen Xiyou, Chen Jianhui, Mu Xianmin, et al. Singlewire power transmission based on spatial electric field coupling: simulation, understanding and construction[J].Proceedings of the CSEE, 2017, 37(19): 5749-5758.
[19] Li Siqi, Liu Zhe, Zhao Han, et al. Wireless power transfer by electric field resonance and its application in dynamic charging[J]. IEEE Transactions Industrial Electronics, 2016, 63(10): 6602-6612.
[20] Liu Chao, Hu A P, Covic G A, et al. Comparative study of CCPT systems with two different inductor tuning positions[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 294-306.