为三相整流器电感和等效电阻；
为六个二极管；
为三个双向开关，由两个IGBT反向连接组成，并输入相同的开关信号；Udc为直流母线电压；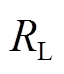
为负载阻抗。摘要 三相三电平Vienna整流器具有开关应力低、功率因数高等优点。为了消除传统无差拍预测电流控制（DPCC）对系统参数的依赖性，该文提出一种无模型预测电流控制（MFPCC）方法，其特点是利用超局部模型代替原有的Vienna整流器精确模型，并利用过去两个时刻的电压和电流信息实现超局部模型的增益和动态部分的在线更新。进一步结合DPCC预测得到下一时刻参考电压矢量，通过空间矢量调制（SVM）得到开关驱动信号。该方法鲁棒性强、计算量小、稳态和动态性能良好。在参数精确和失配的情况下，对传统DPCC和该文所提方法进行稳态和动态性能对比，仿真和实验结果验证了所提方法的优越性。
关键词：Vienna整流器 无模型 预测电抗控制 空间矢量调制
Vienna整流器是1997年奥地利学者提出的一种能量单向流动的整流器[1]，作为特殊的三电平整流器，它的开关应力是传统三电平脉宽调制（Pulse Width Modulation, PWM）整流器的一半，同时拥有功率因数高的优点，不会出现开关器件上下桥臂直通的情况，无需设置死区，在高压大功率场合获得了广泛的应用，如航空直流供电系统、电动汽车充电桩等[2-4]。
为了实现Vienna整流器的单位功率因数控制，学者们提出不同的方法，如电压定向矢量控制（Voltage Oriented Vector Control, VOC）[5]、滞环电流控制（Hysteresis Current Control, HCC）[6]、模型预测控制（Model Predictive Control, MPC）[7]等。其中模型预测电流控制（Model Predictive Current Control, MPCC）因其原理简单、易于实现被广泛关注，其工作原理是通过离散数学模型预测得到下一时刻网侧电流值，然后枚举所有电压矢量得到使代价函数最小的最优电压矢量[7]。传统MPCC在每个控制周期仅能输出单个电压矢量，导致开关频率不固定。文献[8]提出一种基于空间矢量调制（Space Vector Modulation, SVM）的Vienna整流器MPCC，根据整流器模型预测最优电压矢量，结合最优电压矢量和两个基本矢量，利用SVM转换为开关信号，实现固定开关频率控制，降低输入电流总谐波畸变率（Total Harmonic Distortion, THD），但是该方法依赖系统参数的精度。
针对MPCC方法在参数不匹配时导致的性能恶化问题，为了提高参数鲁棒性，文献[9]将自抗扰控制引入PWM整流器的控制中，补偿无模型与外部扰动带来的干扰，鲁棒性较好，但参数设计较为繁琐。文献[10]提出一种基于电流差分的无模型电流预测控制（Model-Free Predictive Current Control, MFPCC），采用过去时刻的电流差分替代基于模型的电流预测，需要在每个采样周期采样两次，对硬件要求较高。文献[11]针对永磁同步电机提出一种改进的MFPCC，在一个控制周期只需一次电流采样，文献[12]也提出类似的改进MFPCC并应用在PWM整流器上。文献[10-12]无需任何系统参数，显著提高了系统的鲁棒性，但是由于存在电流差分更新不及时的问题，稳态性能相对较差。为此，文献[13]提出一种基于超局部模型和SVM的改进MFPCC，通过扩张状态观测器和代数微分法来估计超局部模型的动态部分，在解决参数鲁棒性的同时具有良好的稳态性能，但控制相对复杂，需要调试参数较多。另外，其所用超局部模型中的增益并未进行辨识或估计，一般是通过试凑或经验提前得到，在实际应用有一定局限性。
本文提出了一种改进的基于SVM的MFPCC方法，采用超局部模型代替原有的Vienna整流器精确模型，但是与文献[13]不同，超局部模型的增益和动态部分是在线计算得到，仅利用过去两个时刻的电压和电流信息即可实现超局部模型的在线更新，具有计算量小、通用性强等优点。进一步和无差拍控制结合得到参考电压矢量，并通过SVM生成驱动脉冲，在改善鲁棒性的同时具有良好的稳态和动态性能。该方法的有效性通过Simulink仿真和实际Vienna整流器平台的实验得到了验证。
Vienna整流器的主电路拓扑如图1所示，其中ea、eb、ec为三相电网电压；为三相整流器电感和等效电阻；为六个二极管；为三个双向开关，由两个IGBT反向连接组成，并输入相同的开关信号；Udc为直流母线电压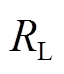；为负载阻抗。
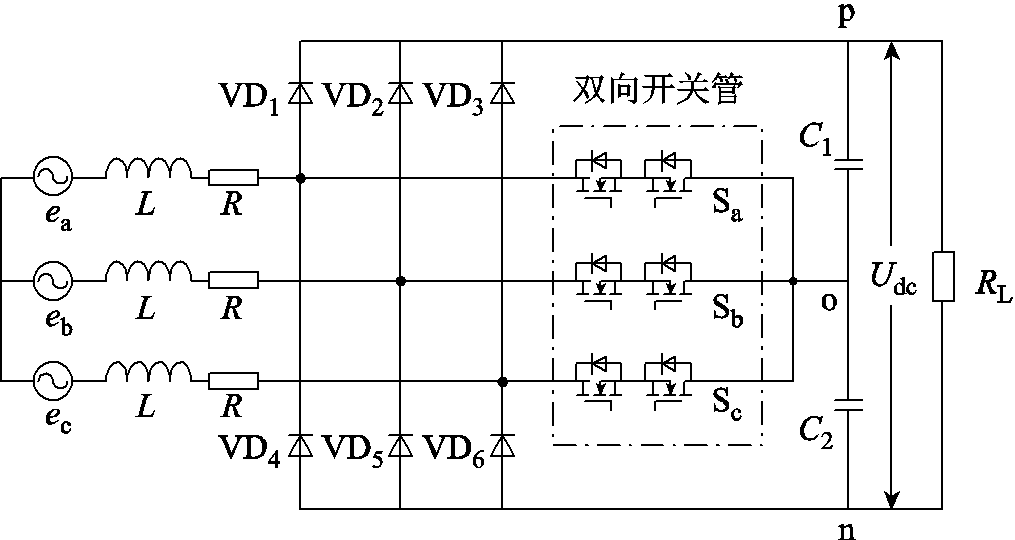
图1 Vienna整流器主电路拓扑
Fig.1 Main circuit topology of Vienna rectifier
定义Vienna整流器的端电压为交流侧端与母线中点之间的电压。当双向开关导通时，直流母线电压被钳位到0。当双向开关关断时，Vienna整流器的交流侧输出电压极性与网侧电流极性相关；当网侧电流大于0时，端电压为Udc/2；当网侧电流小于0时，端电压为-Udc/2。
Vienna整流器的数学模型在两相静止坐标系下可以表示为
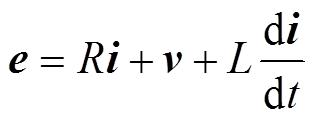（1）
式中，e为网侧电压复矢量；i为网侧电流复矢量；v为交流侧输入电压复矢量；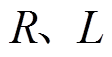
分别为网侧线路电感和线路阻抗。
Vienna整流器网侧复功率S可通过采样得到的电网电压e和电网电流i计算，即
（2）
式中，i*为i的共轭；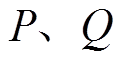
分别为网侧有功功率和无功功率。
在两相静止坐标系下，网侧电流参考值为
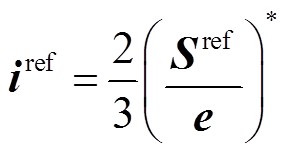（3）
式中，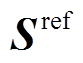
为网侧复功率参考值。
将式（1）采用一阶欧拉法进行离散化，可以得到
（4）
式中，k为采样时刻；Tsc为采样周期。
假设下一时刻电流预测值与当前时刻的电流参考值相同，若网侧输入电流在一个采样周期内实现对参考值的无差跟踪，就能达到无差拍的控制效果。通过Vienna整流器的数学模型可以得到当前时刻交流侧输入电压复矢量为
（5）
将式（5）的电压矢量通过SVM得到开关器件的控制信号，可以实现Vienna整流器的传统无差拍电流预测控制。
三相三电平Vienna整流器的交流侧输出端电压有三种电平状态：
、0、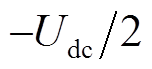
。根据开关状态和电流极性的不同，共有25个电位状态，19个基本电压矢量[14]，其在两相静止坐标系中如图2所示。其中开关状态的对应关系定义为
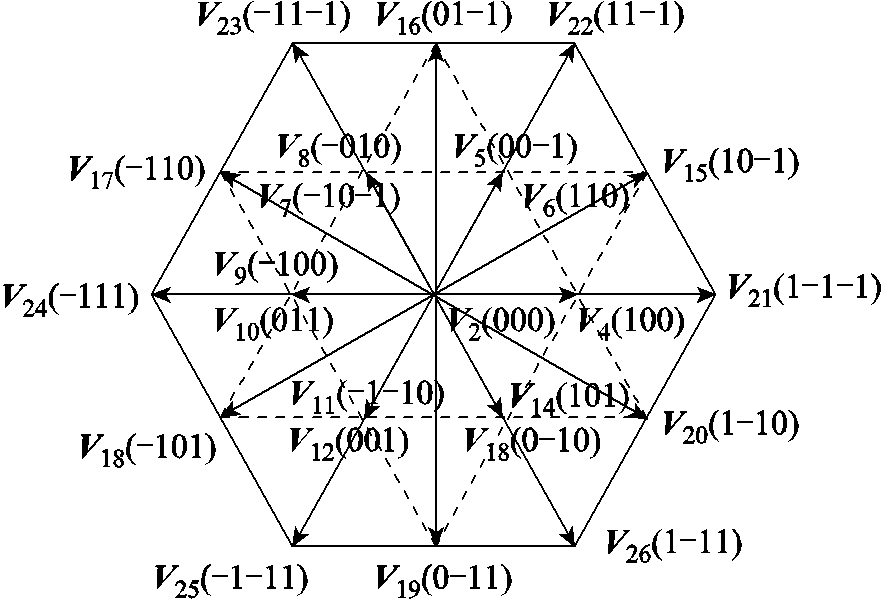
图2 三相三电平Vienna整流器基本电压矢量
Fig.2 Basic voltage vector of three-phase three-level Vienna rectifier
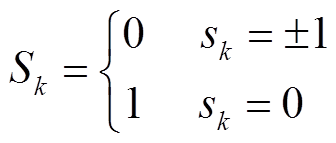（6）
式中，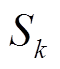
为双向开关的通断状态；
；
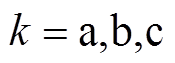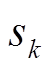为引入的开关函数[15]。
需要注意的是，在同一种电流极性下，Vienna整流器只有八种开关状态，因此可以选择的基本电压矢量只有8个，包括000、001、010、011、100、101、110、111。
传统无差拍预测控制对系统模型参数的精确度要求高，本文提出改进的MFPCC，将Vienna整流器系统定义为超局部模型，不需要系统任何参数，具有较强的鲁棒性。Vienna整流器为一阶系统，将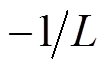
记为
，
记为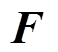
，结合式（1）可以得到其超局部模型为
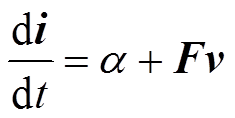（7）
式中，为系统的增益系数；F为系统未知的部分和可能的干扰。对式（7）进行离散化，可以得到Vienna整流器的MFCC离散超局部数学模型[16]为
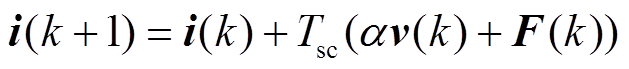（8）
将
电压矢量下的网侧电流差分表示为
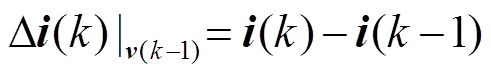（9）
同理可以得到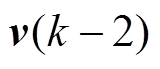
电压矢量下的网侧电流差分为
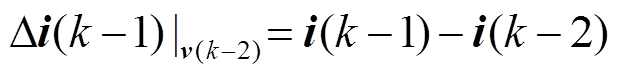（10）
结合式（9）和式（10），可以得到Vienna整流器
和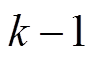
采样时刻的电流差分记为
（11）
（12）
当采样频率足够高时，假设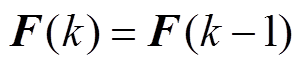
，结合式（11）和式（12）求得
（13）
将式（13）代入式（11）中可以得到
（14）
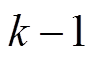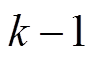将式（13）和式（14）代入式（8），得到时刻的网侧预测电流。由于数字控制中固有的采样延迟，在第时刻所选的电压矢量直到时刻才被应用[17]。进行延迟补偿并结合式（5）可得
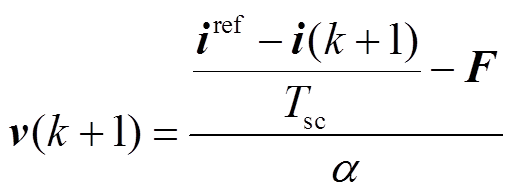（15）
Vienna整流器采用基于SVM的MFPCC方法控制框图如图3所示。
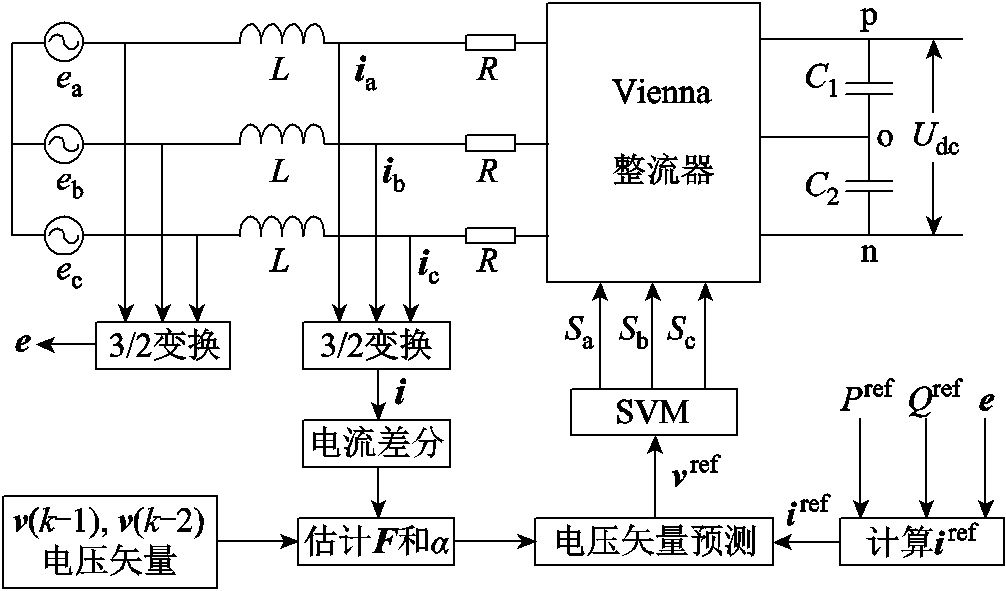
图3 Vienna整流器基于SVM的MFPCC控制框图
Fig.3 SVM-based MFPCC control block diagram of Vienna rectifier
为了验证所提方法的优越性，对三相三电平Vienna整流器进行仿真和实验验证。为了实现单位功率因数，无功功率参考值设置为0。控制器中的电感参数L设定为实际精确值的kc倍，在本文中令其按照0.5→0.75→1→1.25→1.5的规律变化，从而能够验证本文方法和传统方法在电感参数精确与失配时的效果。其系统主要参数见表1。
表1 Vienna整流器系统主要参数
Tab.1 The system parameters of Vienna rectifier
参数数值 交流侧相电压有效值/V50 频率/Hz50 交流侧电感/mH0.5 交流侧等效电阻/W0.5 直流母线电容/mF1 720 采样频率/kHz20 负载电阻/ W100
3.1.1 稳态性能和鲁棒性
三相三电平Vienna整流器在线路电感L失配情况下传统DPCC和本文所提MFPCC的控制效果如图4所示，有功功率参考值为500W，电感
图4表明，传统DPCC依赖系统参数L的准确性，当电感不准确时电流谐波增大，有功功率和无功功率脉动增加。需要注意的是，Vienna整流器作为能量单向流动的变换器，有功功率不能为负。本文所提MFPCC参数鲁棒性强，稳态性能良好。
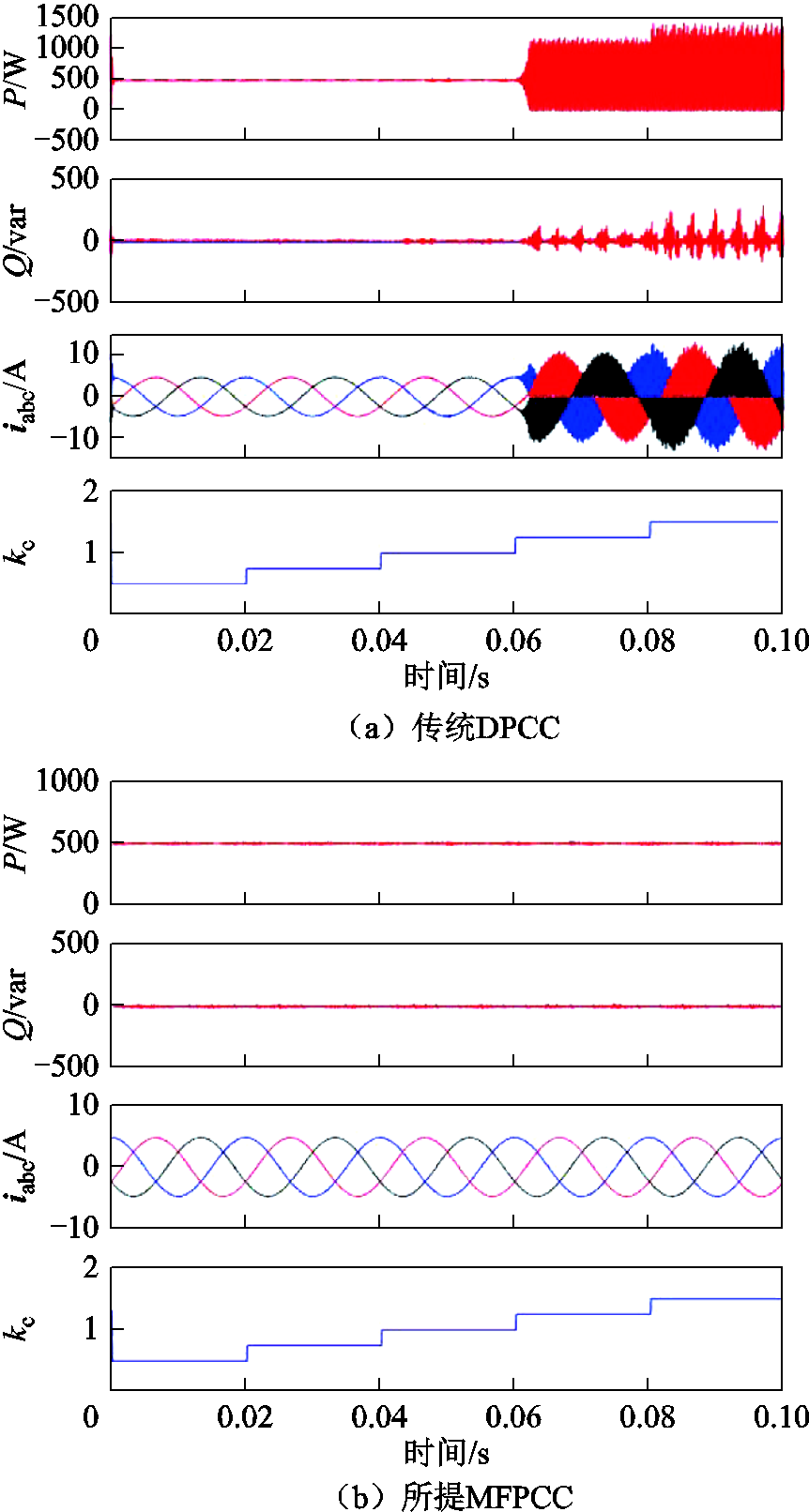
图4 参数L失配时传统DPCC和所提MFPCC的稳态响应仿真
Fig.4 Steady-state response simulation of traditional DPCC and proposed MFPCC methods when parameter L is mismatched
3.1.2 动态性能
Vienna整流器在功率阶跃情况下传统DPCC和本文所提MFPCC方法仿真的控制效果如图5所示，有功功率参考值从200W阶跃到500W。图5表明本文所提方法动态性能良好，在有功功率阶跃时，无冲击电流，相比传统DPCC方法，有功功率和无功功率脉动小。两种方法的直流电压在有功功率阶跃时随之上升至稳定值，约0.15s后稳态运行，具有较好的动态性能。
图5 传统DPCC和所提MFPCC的功率阶跃响应仿真
Fig.5 Power step response simulation of traditional DPCC and proposed MFPCC methods
THD分析见表2，可以看出通过功率阶跃两种方法网侧电流THD都有所减小，本文所提的MFPCC方法网侧电流正弦度更高。
表2 Vienna整流器功率阶跃仿真网侧电流THD分析
Tab.2 Grid-side current THD analysis of Vienna rectifier power step simulation
功率给定参考值/WTHD（%） 传统DPCC所提MFPCC 2008.935.32 5004.261.61
搭建三电平Vienna整流器实验平台，如图6所示，对其进行传统DPCC和本文所提MFPCC方法控制。
图6 Vienna整流器实验平台
Fig.6 Experimental platform of Vienna rectifier
3.2.1 稳态性能和鲁棒性
Vienna整流器在线路电感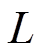
不准确时传统DPCC方法和本文所提MFPCC方法的实验结果如图7所示。有功功率参考值为500W，电感
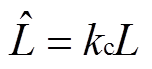。可以明显看出，由于三电平Vienna整流器电感参数较小，传统DPCC对电感参数敏感，在电感增大时网侧电流畸变严重，有功功率和无功功率脉动变大；而本文所提的MFPCC方法在电感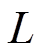不准确时，控制效果良好，不受其影响，参数鲁棒性强，与仿真结果基本一致。
图7 参数L失配时传统DPCC和所提MFPCC的稳态响应实验
Fig.7 Steady-state response experiment of traditional DPCC and proposed MFPCC methods when parameter L is mismatched
3.2.2 动态性能
Vienna整流器在功率阶跃时传统DPCC和本文所提MFPCC的控制效果如图8所示，有功功率参考值从200W阶跃到500W。图8表明，采用传统DPCC方法在进行功率阶跃时网侧电流和有功功率有冲击，重新进入稳态后有功功率脉动大；本文所提MFPCC动态效果良好，无冲击功率和电流，有功功率脉动相较传统DPCC小。两种方法的直流电压在有功功率阶跃时随之上升至稳定值，约0.15s后稳态运行，没有冲击与波动，具有较好的动态性能。
图8 传统DPCC和所提MFPCC的功率阶跃响应实验
Fig.8 Power step response experiments of traditional DPCC and MFPCC methods
对不同功率下的网侧电流进行THD分析，结果见表3，表明本文采用基于SVM的MFPCC方法稳态性能良好，电流THD低。
表3 Vienna整流器功率阶跃实验网侧电流THD分析
Tab.3 Grid-side current THD analysis of Vienna rectifier power step experiment
功率给定参考值/WTHD（%） 传统DPCC所提MFPCC 2009.138.69 5007.694.39
本文提出了一种基于SVM的MFPCC方法，与传统DPCC相比，此方法不依赖整流器模型与系统参数。通过储存前两个时刻的电流差分及对应的电压矢量，从而重构出系统的超局部模型并实现在线更新。基于该模型预测下一时刻电压矢量，再经由SVM转换成开关信号。通过与传统DPCC方法进行仿真与实验验证比较，可以证明该方法鲁棒性强，稳态和动态性能良好。
参考文献
[1] Kolar J, Zach F. A novel three-phase utility interface minimizing line current harmonics of high-power telecommunications rectifier modules[J]. IEEE Transactions on Industrial Electronics, 1997, 44(4): 456-467.
[2] 李萍, 王久和, 李建国, 等. 单向混合整流器无源电流控制[J]. 电工技术学报, 2020, 35(21): 4511-4523.
Li Ping, Wang Jiuhe, Li Jianguo, et al. A passivity-based current control strategy for unidirectional hybrid rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4511-4523.
[3] 郝振洋, 徐子梁, 陈宇, 等. 航空Vienna整流器故障诊断与容错控制[J]. 电工技术学报, 2020, 35(24): 5152-5163.
Hao Zhenyang, Xu Ziliang, Chen Yu, et al. Fault diagnosis and fault tolerant control for aviation Vienna rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5152-5163.
[4] 肖蕙蕙, 苏新柱, 郭强, 等. 三相Vienna整流器无网压传感器预测电流控制策略[J]. 电工技术学报, 2021, 36(6): 1304-1312.
Xiao Huihui, Su Xinzhu, Guo Qiang, et al. Predictive current control of three-phase Vienna rectifier without grid voltage sensors[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1304-1312.
[5] Rajendran G, Vaithilingam C, Misron N, et al. Voltage oriented controller based Vienna rectifier for electric vehicle charging stations[J]. IEEE Access, 2021, 9: 50798-50809.
[6] 杨頔, 姚钢, 周荔丹. 功率变化环境下的四线制Vienna整流器优化联合控制方法[J]. 电工技术学报, 2021, 36(2): 305-319.
Yang Di, Yao Gang, Zhou Lidan. An improved control method of 4-wire Vienna rectifier considering power fluctuation[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 305-319.
[7] 张锦, 於锋, 高磊, 等. Vienna整流器模型预测电流控制优化方案研究[J]. 电源学报, 2020, 18(5): 110-117.
Zhang Jin, Wu Feng, Gao Lei, et al. Research on optimal scheme of Vienna rectifier model predictive current control[J]. Journal of Power Supply, 2020, 18(5): 110-117.
[8] Huang Xiping, Yang Zekun, Chen Guitao, et al. Model predictive control of current with fixed switching frequency on VEINNA rectifier[C]//2020 Chinese Control and Decision Conference (CCDC), Hefei, 2020: 2392-2397.
[9] 王久和. 电压型PWM整流器的非线性控制[M]. 北京: 机械工业出版社, 2015.
[10] Lin Chengkai, Liu Tianhua, Yu Jente, et al. Model-free predictive current control for interior permanent-magnet synchronous motor drives based on current difference detection technique[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 667-681.
[11] 张虎, 张永昌, 刘家利, 等. 基于单次电流采样的永磁同步电机无模型预测电流控制[J]. 电工技术学报, 2017, 32(2): 180-187.
Zhang Hu, Zhang Yongchang, Liu Jiali, et al. Model-free predictive current control of permanent magnet synchronous motor based on single current sampling[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 180-187.
[12] 张永昌, 焦健, 刘杰. 电压型PWM整流器无模型预测电流控制[J]. 电气工程学报, 2018, 13(6): 1-6.
Zhang Yongchang，Jiao Jian，Liu Jie. Model-free predictive current control of voltage type PWM rectifier[J]. Journal of Electrical Engineering, 2018, 13(6): 1-6.
[13] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model-free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[14] 王涛, 陈昌松, 段善旭, 等. 用于改善电流过零点畸变的Vienna整流器空间矢量调制策略[J]. 电工技术学报, 2019, 34(18): 3854-3864.
Wang Tao, Chen Changsong, Duan Shanxu, et al. Space vector modulation strategy of Vienna rectifier for improving current zero-crossing distortion[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3854-3864.
[15] 杨玉波, 谢运祥. 三电平Vienna整流器的一种简化SVPWM算法[J]. 电气应用, 2015, 34(11): 54-57.
Yang Yubo，Xie Yunxiang. A simplified SVPWM algorithm for three-level Vienna rectifier[J]. Electrotechnical Application, 2015, 34(11): 54-57.
[16] Zhang Yongchang, Wang Xing, Yang Haitao, et al. Robust predictive current control of induction motors based on linear extended state observer[J]. Chinese Journal of Electrical Engineering, 2021, 7(1): 94-105.
[17] Zhang Yongchang, Min Zeyu. Model-free predictive current control of a pwm rectifier based on space vector modulation under unbalanced and distorted grid conditions[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(2): 2319-2329.
Model Free Predictive Current Control of Vienna Rectifier Based on Space Vector Modulation
Abstract The three-phase three-level Vienna rectifier has the advantages of low switching stress and high power factor. In order to eliminate the dependence of traditional deadbeat predictive current control (DPCC) on system parameters, a model-free predictive current control (MFPCC) method is proposed in this paper. The features of the proposed method include using an ultra-local model instead of the conventional accurate model of the Vienna rectifier, and the online updating of the gain and the dynamic part of the ultra-local model based on the voltage/current information in the past two control periods. The proposed method is combined with DPCC to calculate the reference voltage vector at the next instant and space vector modulation (SVM) is used to generating the gating pulses. The proposed method has strong robustness, small amount of calculation, and good steady and dynamic performance. The proposed method is compared to conventional DPCC in terms of steady-state and dynamic performance under the condition of accurate and inaccurate model parameters. Simulation and experiment results verify the superiority of the proposed method.
keywords: Vienna rectifier, model free, predictive control, space vector modulation (SVM)
DOI:10.19595/j.cnki.1000-6753.tces.211753
中图分类号：TM61
国家自然科学基金（52077002）、国家重点研发计划（2021YFB2400702）和华能集团总部科技项目海上风电与智慧能源系统科技专项（一期）（HNKJ20-H88）资助。
收稿日期 2021-11-01
改稿日期 2021-11-30
张永昌 男，1982年生，教授，博士生导师，研究方向为电力电子与电机控制。E-mail：zyc@ncepu. edu. cn（通信作者）
屈祈延 女，1996年生，硕士研究生，研究方向为Vienna整流器控制。E-mail：qqyan213@163.com
（编辑 赫蕾）