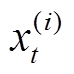为用户i在时刻t缺失的量测值，按式（1）对该点数据进行修正。摘要 识别海量居民用户的用电行为模式并进行合理分类，可为需求侧精益化管理提供辅助决策。该文提出一种基于卷积神经网络自动编码器与层次聚类多任务联合模型的居民用电模式分类方法。首先，提出基于同时刻量测数据均值的缺失值填补方法和基于季节性极端学生化偏差检验的异常点检测方法，对海量且高维的用电数据进行数据清洗与修正；其次，利用卷积神经网络自动编码器对居民用电数据进行特征提取，获取可表征用户用电行为的特征向量；然后，结合层次聚类算法以及轮廓系数指标确定用户聚类个数以及聚类中心向量，并利用聚类中心向量初始化神经网络聚类层，进行用户聚类，将特征提取过程与用户聚类过程进行联合，组成多任务学习神经网络，实现端到端的用电模式分类；最后，结合环境温度和电价影响因素，在实际数据集进行验证。
关键词：居民负荷 负荷聚类 卷积神经网络 自动编码器 联合模型
居民负荷是电力负荷的重要组成部分，有效分析居民用户的用电特性有助于洞悉用户用电行为模式，为需求侧精益化管理、分时电价制定及新能源就地消纳等应用提供决策支撑，协助电力公司在保障民生的同时，进一步推动实现“碳中和”[1-5]。然而居民智能电表所量测的用电数据高维且海量，数据质量不一，蕴含大量非线性关系[6]。并且居民负荷之间的用电特性差异大[7]，负荷调控潜力各不相同。如何针对海量居民用户进行精准的用电模式分类，把握其用电行为与能耗模式，成为推动电力供需互动发展亟需解决的问题。
海量用户的用电模式分类通常利用聚类算法将具有相似用电行为模式的用户划分为同一类别[8]，其主要可分为直接聚类法和间接聚类法。直接聚类以用户用电数据作为输入，利用聚类算法进行分类。在文献[9-12]中，分别采用改进Kmeans算法、模糊C均值聚类和动态聚类算法对电力用户的日负荷曲线进行分类。文献[13]结合时间序列的动态时间扭曲距离和密度峰值聚类方法获取典型负荷曲线。然而将高维的用电数据直接进行聚类难以提取复杂的用电行为变化特性，若仅采用单个典型日的负荷数据又难以考虑负荷在长时间尺度上的时序变化特性。
间接聚类主要利用特征提取方法减少数据维度后再进行聚类。典型的特征提取方法包含人工特征提取法与降维算法等。人工特征提取法通过用电曲线的用电特征指标表征用户用电行为[8]，例如，日最大负荷、日负荷率、不同用电时间段的平均负荷等指标[14-15]。但以上指标难以描述用户用电行为的时序变化特性，所以许多研究引入降维算法进行分析。文献[16-17]引入分段聚合近似法及深度置信网络对负荷曲线进行近似。文献[18-19]采用主成分分析法对用户量测数据进行降维，然而该算法属于线性降维，难以考虑数据间的非线性关系。文献[20]提出一种基于长短期记忆网络自动编码器的负荷聚类方法，但是长短期记忆网络的输入需是单个且连续的时间序列，难以实现多用户的分类。
针对以上问题，本文提出了基于卷积神经网络自动编码器（Convolutional Neural Networks Auto-Encoder, CNN-AE）与层次聚类联合模型的居民用电模式分类方法。首先，提出一种基于同时刻量测数据均值（Mean Value of Simultaneous Data, MVSD）的缺失值填补方法和基于季节性极端学生化偏差检验（Seasonal Hybrid Extreme Studentized Deviate Test, S-H-ESD）的异常点检测方法，减小数据缺失值以及异常值对模型分类的影响；其次，提出一种用于用电行为特征提取和用户聚类的联合神经网络模型，该模型通过CNN-AE对居民用电数据进行特征提取，挖掘其内在非线性关系以及时序变化特性，获取表征居民用电行为的特征向量，同时结合层次聚类算法自定义一个神经网络层用于用户聚类；然后，将特征提取模型与用户分类模型进行联合，组成多任务学习神经网络模型；最后，通过联合模型的部分神经网络参数共享，同步优化其特征提取误差与聚类误差，避免特征提取模型过拟合的同时降低用户聚类的误差，实现端到端的居民用电模式分类，并结合环境温度和电价因素，在实际公开数据集中验证了本文方法的有效性。
由于居民用户智能电表在量测及信息传输过程中会存在量测误差和数据上传失败等问题，导致量测数据存在数据缺失、异常，从而影响模型准确。同时考虑到神经网络模型对训练数据的输入维度有严格要求，所以需要对数据集进行预处理清洗及修正。针对此问题，本文提出基于同时刻量测数据均值的缺失值填补方法和基于季节性极端学生化偏差检验算法的异常点检测方法。通过计算MVSD数值对数据缺失值进行填补，并利用S-H-ESD算法对用户的用电数据进行异常检测。将所检测出的异常点数值重新定义为缺失值，并再次进行填补，直至完成对整个数据集的清洗。
基于MVSD的缺失值填补方法利用智能电表相同时刻量测数据的均值对该时刻的缺失值进行填补。假设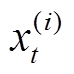为用户i在时刻t缺失的量测值，按式（1）对该点数据进行修正。
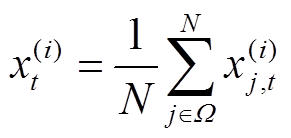（1）
式中，Ω为在t时刻有量测值的日期集合，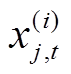
为用户i在日期j内t时刻的量测值；N为Ω中日期个数。
为了减小异常值对算法模型的影响，提出基于S-H-ESD算法的居民用户量测数据异常点检测方法。该方法结合时间序列分解的季节性成分和绝对中位差（Median Absolute Deviation, MAD）对ESD算法进行改进，提升了对高占比异常数据时间序列异常检测的鲁棒性。
假设被检测的单变量时间序列为X，首先对该时间序列进行时序分解，获取该时间序列的周期分量SX，并计算余项分量Y与绝对中位差dMAD，计算方法为
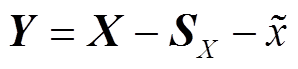（2）
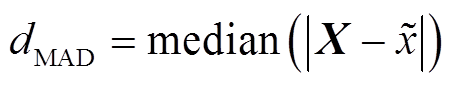（3）
式中，
为时间序列X的中位数；median为取变量中位数。
再计算余项分量Y与均值偏离最远的残差Rj，计算公式为
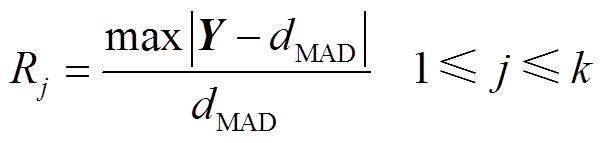（4）
式中，j为残差的计算次数；k为时间序列的异常点存在个数。
完成残差计算之后，计算对应的t分布的临界值λj，其计算公式为
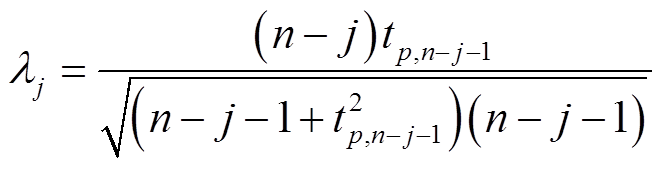（5）
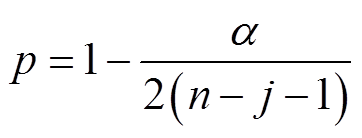（6）
式中，n为被检测时间序列的样本数；tp,n-j-1为显著度等于p、自由度为n-j-1时的t分布的临界值；α为所选取的置信度水平大小，在本文中α取0.95。
当Rj＞λj，则定义该样本点为异常数据点。完成一次异常值检测之后，在进行下一次计算时，应删除上一轮计算的最大残差样本数据，并重新计算，直到完成所有样本的检测。
自动编码器是一种数据压缩的算法，具有良好的非线性特征提取能力，可以获取能够代表输入数据结构以及隐藏非线性特性的特征向量。最基本的自动编码器神经网络结构如图1所示。
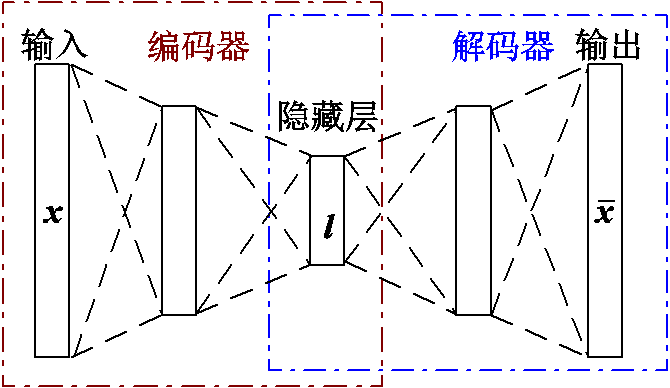
图1 自动编码器示意图
Fig.1 Schematic diagram of auto-encoder
该模型主要由两部分组成，一个可由函数l=f（x）表示的编码器和一个可由函数
表示的用于生成重构数据的解码器，其中l表示自编码神经网络内部隐藏层向量。
当给定输入向量
时，经过编码器的编码处理之后得到隐特征向量
并且d＜n，然后再次经过解码器将隐特征向量转换为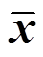
，自编码器的优化目标为最小化输入x与输出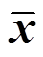之间的重建误差。隐特征向量l相比于输入数据，其维度大幅减少，但包含了输入数据的关键信息，通过对隐特征向量的处理分析，可以减少计算代价。对于自编码器神经网络的选取，CNN由于其强大的序列数据特征提取能力，已经在处理电力系统时间序列问题中验证了其优越性[21]。所以选用CNN-AE进行特征提取，通过重建用电序列数据，将数据降维至低维的特征向量，便于后续的分析。
层次聚类通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树，聚类质量高[22]。假设利用所提出的模型针对用户i所提取的特征向量为Xi，用户j的特征向量为Xj，选择欧式距离作为聚类相似性度量，则用户i与用户j之间的距离相似度di, j为
（7）
所以对于N个用户数据的输入，则用户间的距离相似度矩阵DM为
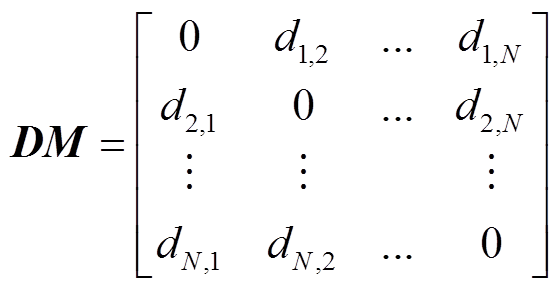（8）
在矩阵DM中，对距离值最小的两个数据点进行组合，再次计算距离相似度矩阵。对于组合后数据点（j, k）与单个数据点m的距离相似度d(j,k),m计算方法为
（9）
再次寻找计算后未被组合的数据点距离相似度的最小值，并对其组合。完成所有数据点组合后，对于组合间的距离，选取两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离，将距离值最小的两个数据点再次进行合并，依此类推，直到完成所有数据的合并，形成层次聚类树。
传统的间接用户分类方法先进行特征提取，再利用聚类算法进行分类。然而特征提取过程中只考虑数据的信息损失误差，聚类算法只考虑分类误差，未在两个计算模型之间建立联系，所以会导致降维算法所提取的特征向量并不是最优的用于区分用户相似程度的向量。为了将聚类计算过程结合到特征提取过程中，提出一种基于CNN-AE与层次聚类算法的联合模型，其具体结构如图2所示。
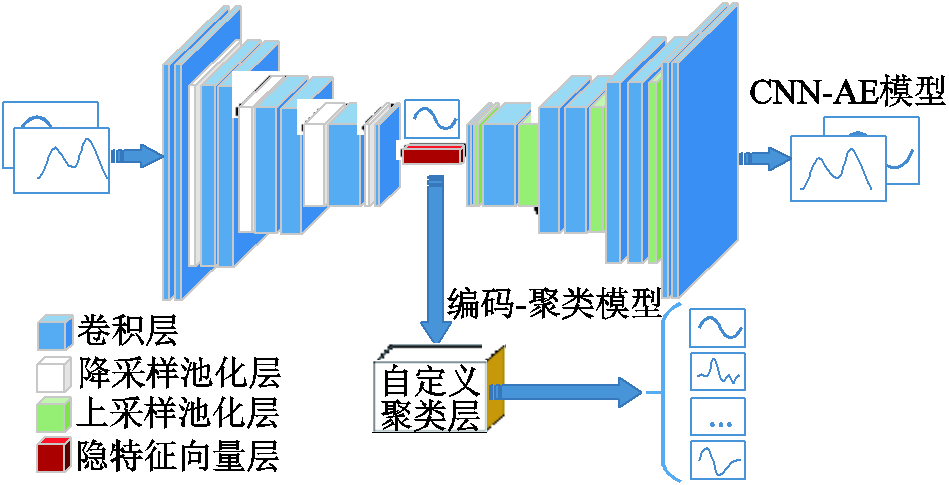
图2 联合模型结构
Fig.2 Structure diagram of joint model
具体地，整个模型可分为CNN-AE模型和编码-聚类模型两个子模型。由于居民的用电数据高维且蕴含大量非线性关系，利用CNN-AE可有效对这些序列数据进行特征提取，降低数据维度的同时获取可代表用户用电行为特性的特征向量。编码-聚类模型负责对CNN-AE的编码器部分所提取的特征向量进行聚类，得到最终的用户聚类结果。下面对这两个模型进行详细分析。
CNN-AE的学习目标是获取能够代表用户典型用电特性的特征向量。对于CNN-AE的网络架构选取，本文选择对计算机视觉领域经典网络VGGNET-16进行改进。VGGNET-16相比简单的图像处理网络例如LeNet、AlexNet，其层数更深，对数据的特征提取能力更强，同时相较其他大型的图像处理网络，其结构简单，减少了计算成本的同时保证了模型的精确度。传统的VGGNET-16神经网络在进行卷积池化特征提取操作之后，将获得的特征向量进行展平，再紧接多个全连接层，最终实现图像分类等应用。由于需要对用户的用电时间序列进行特征提取，所以将其神经网络架构转换为自编码结构。考虑到卷积神经网络层数过多会导致过拟合，对典型VGGNET-16进行简化改进，减少一定的特征提取层数。经改进后的模型首先利用卷积层与降采样池化层对用电序列数据进行特征提取，得到隐特征向量，再通过逆卷积层与上采样池化层对隐特征向量进行重构，并基于数据的重建误差进行反向传播调整神经网络权重。本文选用方均误差作为数据重建误差的衡量指标，所以该模型的损失函数LCA为
（10）
式中，n为居民用户数量；Xi为用户i的实际用电序列；
为经过自编码器编码与解码重构之后用户i的用电序列。
假设居民用户的用电序列每隔半小时采样一次，则一天采样点数为48个，对于n个量测用户m天的输入数据维度为（n, m, 48, 1）。需要指出的是，这里将量测天数作为通道数放在输入维度第二位，与传统的图像识别输入数据并不完全相同。输入数据经过CNN-AE的编码与解码处理之后，其输出维度仍为（n, m, 48, 1），中间层隐特征向量维度选取为（1, 48）。
编码-聚类模型由CNN-AE的编码层和自定义聚类层组成，其中自定义聚类层的主要计算步骤如下：
（1）初始化自定义聚类层权重。首先利用CNN-AE模型对输入数据进行预训练，得到隐特征向量，再利用层次聚类算法对隐特征向量进行初步聚类，获取各个类别的聚类中心向量，并将其设置为自定义聚类层的网络参数权重。假设用户群体总聚类个数为k，单用户的用电特征向量输出维度为（1, l），则自定义网络层的权重参数的维度为（k, l）。
（2）特征向量获取。完成聚类层权重初始化之后，通过CNN-AE的编码器部分获取能够代表用户用电特性的隐特征向量，作为自定义聚类层的输入。
（3）距离相似度计算。计算每一个居民用户的隐特征向量与自定义聚类层中每一个聚类中心之间的欧式距离，分别记为（di1, di2, …, dik），其中dij（1≤j≤k）表示用户i与第j类聚类中心之间的欧式距离相似度。
（4）距离相似度转换。为了更确切地将步骤（3）的计算结果转换为该用户所属该聚类中心的概率，可利用学生t分布将距离相似度转换为概率分布q，其转换公式为
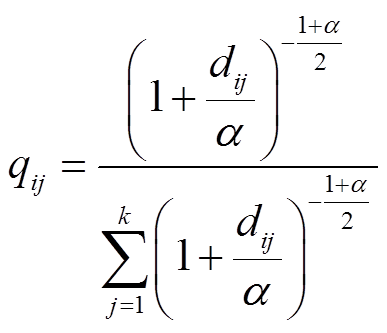（11）
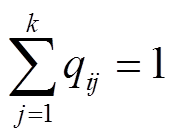（12）
式中，qij为用户i属于类别j的概率；在非监督学习中可设置α=1。
通过自定义聚类层计算，可得到每个用户所属各个类别的概率，为了定义聚类层的损失函数，本文引入Kullback-Leibler散度（KL散度）指标。KL散度又称为相对熵，是两个概率分布间差异的非对称性度量，其具体的推导过程见附录。所以除已有概率分布q外，还需引入辅助目标概率分布p。参考文献[23]，可设置辅助概率分布p为
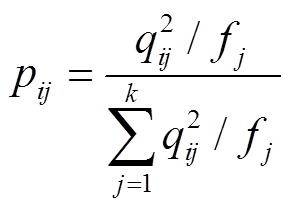（13）
（14）
式中，pij为用户i属于类别j的辅助概率值。
所以根据KL散度的定义，自定义聚类层的损失函数Lcluster可写为
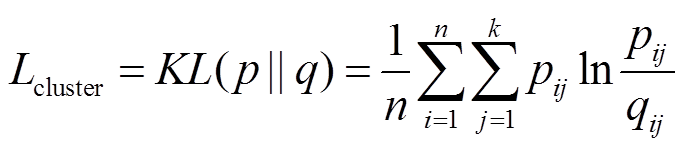（15）
需要注意的是，在步骤（1）初始化自定义聚类层权重时，需利用层次聚类算法在模型外部先确定聚类的个数。在未知实际分类类别数情况下，本文引入聚类指标轮廓系数（Silhouette Coefficient, SC）衡量聚类效果的好坏。单个样本c的轮廓系数Sc计算公式为
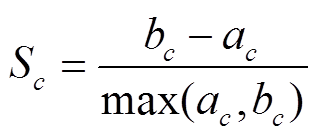（16）
式中，ac为样本c与其所属类中其他样本的平均距离；bc为样本c与其他类样本的平均距离。对于整个数据集的聚类结果的SC计算公式为
（17）
SC的取值范围为[-1,1]，其取值越大，代表聚类的效果越理想。结合聚类个数大小与SC指数之间变化关系可确定最终的聚类个数。
完整的分类模型将CNN-AE模型和编码-聚类模型进行联合，组成多任务学习神经网络。多任务学习可通过部分神经网络参数共享，不同任务之间可以相互学习。本文将两个子模型的损失函数进行累加，得到整个联合模型的损失函数L为
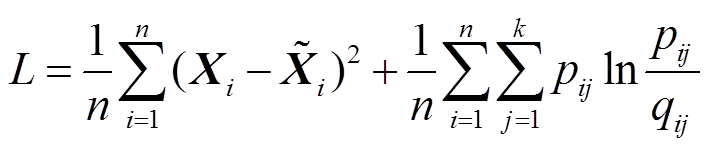（18）
通过该损失函数可以将两个子模型进行联合，利用Adam求解器同步优化CNN-AE的重建误差和编码-聚类模型的分类误差。在特征提取的同时，也可实时计算分类结果。并且编码-聚类模型可通过KL散度误差调整CNN-AE编码器部分的神经网络参数，实现端到端的居民用电模式分类。用户分类整体的计算流程如图3所示。
本文所选用的数据集来自Low Carbon London project下的Smart meter energy consumption data in London households[24]，数据集包含5 567个居民用户每半小时的用电量（一天48个采样点，单位kW·h）。整个数据集被分为两种用电模式客户，第一种为固定电价用户，第二种为动态电价用户。该数据集提供了2013年全年的实时电价，所以本文选择2013年全年的数据进行分析，经去除部分无效量测用户后，还包含3 946个固定电价用户，1 016个动态电价用户。对筛选后用户数据进行缺失值填补与异常点检测处理，得到清洗后数据。
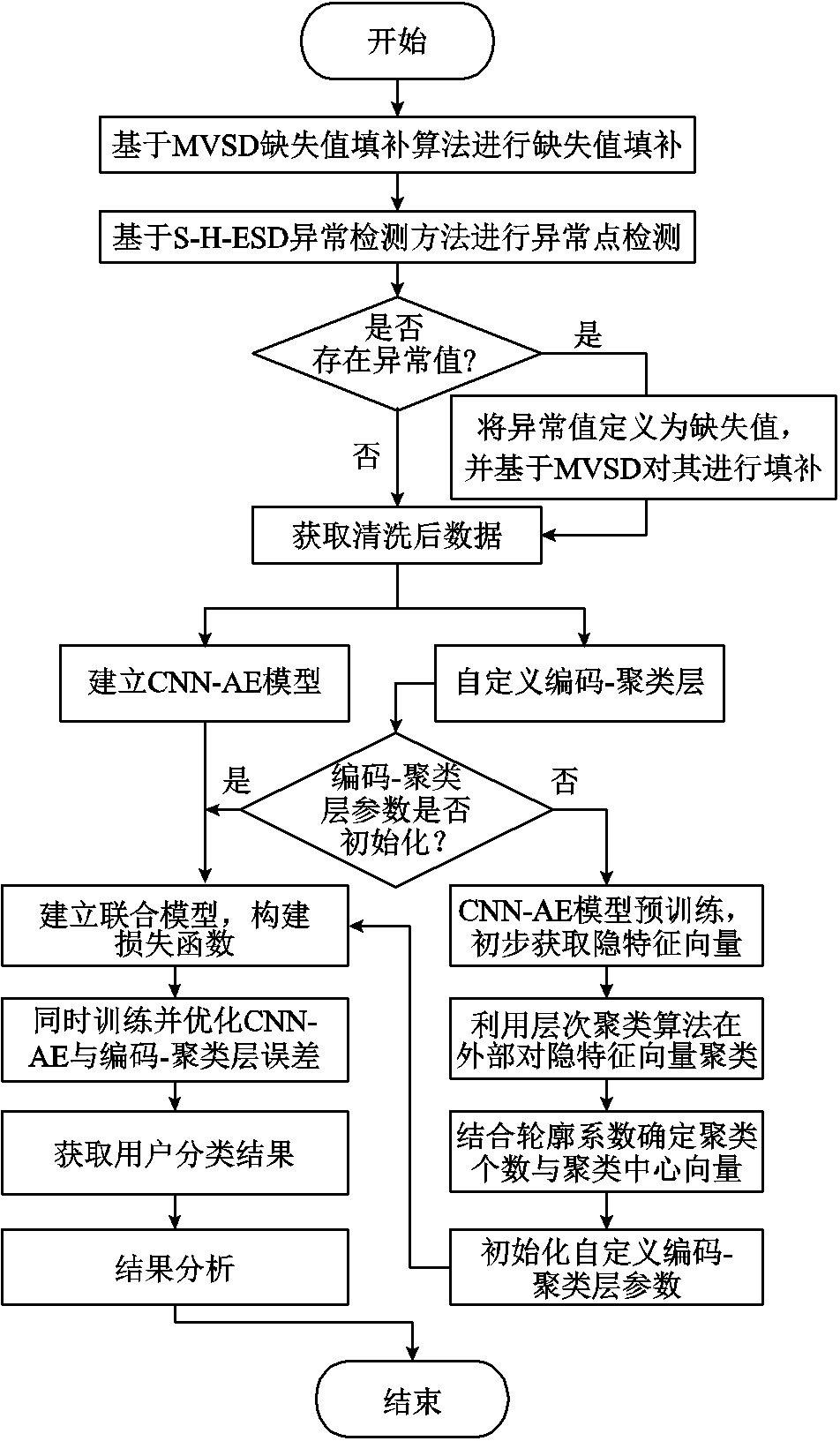
图3 用户分类整体计算流程
Fig.3 Overall calculation flow chart of consumer classification
考虑到数据集包含两种不同类型的用户，动态电价用户可能会参与电价激励响应导致用电特性发生改变，所以为了更加精确地对用户进行分类建模，对两种类型用户进行分别分析。同时由于居民用户的用电行为与外界温度密切相关，所以本文另结合伦敦地区2013年的月平均温度，其变化情况如附图1所示。从附图1可知，1月、2月、3月、4月、11月、12月的平均温度全部低于10℃，其他月份的平均温度则高于10℃。所以结合温度以及电价类型因素将整个数据集划分为四个子数据集，划分结果见表1。
表1 考虑电价与温度因素的数据集划分结果
Tab.1 Dataset division results considering electricity price and temperature factors
数据集名称用户电价类型包含月份每月平均温度/℃ 1固定电价1～4,11～12<10 2固定电价5～10>10 3动态电价1～4,11～12<10 4动态电价5～10>10
对于动态电价用户，其电价类型分为高电价（67.20p/(kW·h)）、正常电价（11.76p/(kW·h)）及正常电价（3.99p/(kW·h)），其中p为货币单位便士。电力运营商会根据当地配网的运行状态以及可再生能源的发电情况将未来一天各个时段的电价提前一天通过短信等方式发送给用户，由用户决定是否改变自身的用电行为。
如3.2节所述，在初始化自定义聚类层权重时，需先确定聚类个数。对四个数据集分别进行预训练特征提取、聚类之后，结合SC指标确定各个数据集的聚类个数。各个数据集的SC指标大小与聚类个数之间的关系如图4所示。
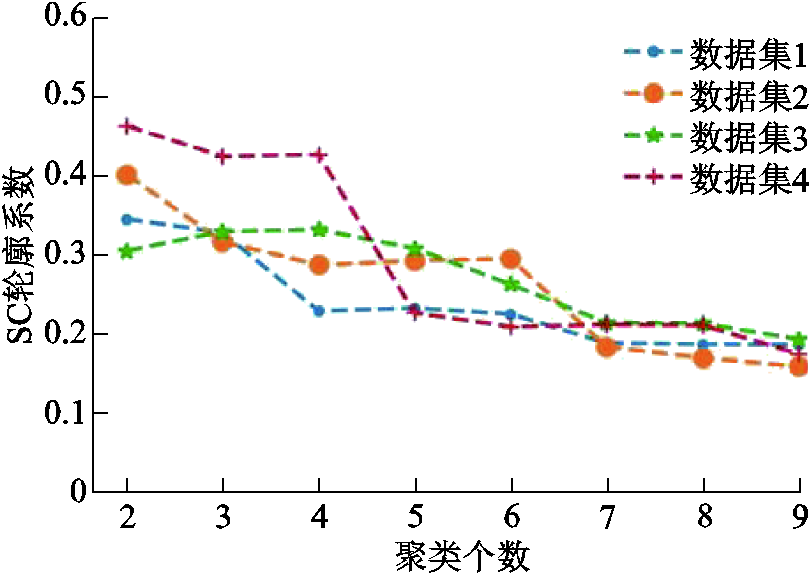
图4 聚类个数与SC指标变化关系
Fig.4 Correlation between the number of clusters and SC index
由图4可知，对于数据集1和数据集2，在聚类数为2时取得最大的轮廓系数；对于数据集3和数据集4，分别在聚类数为4和2时取得最大轮廓系数。考虑到用户分类在智能电网中的应用，以及为能源零售商、负荷聚合商的政策制定提供支持，所选的聚类个数不宜过大，也不宜过小[25]。所以综合SC的变化曲线，选取各个数据集的聚类个数为3。
4.2.1 固定电价用户分析结果
首先对固定电价用户进行分析，经过本文所提出的模型进行用户分类之后，对同类用户各个时间点的用电数据绘制箱线图得到该类用户的典型用电箱线图。箱线图可以反映用电数据的分布特征，能显示出一组数据的最大值、最小值及上下四分位数等，并用绿色标记标识出平均值。对同类别的每个用户的各个时间点量测值取均值，得到该类所有用户的典型用电曲线。数据集1中各类用户的典型用电箱线图与典型用电曲线如图5所示。
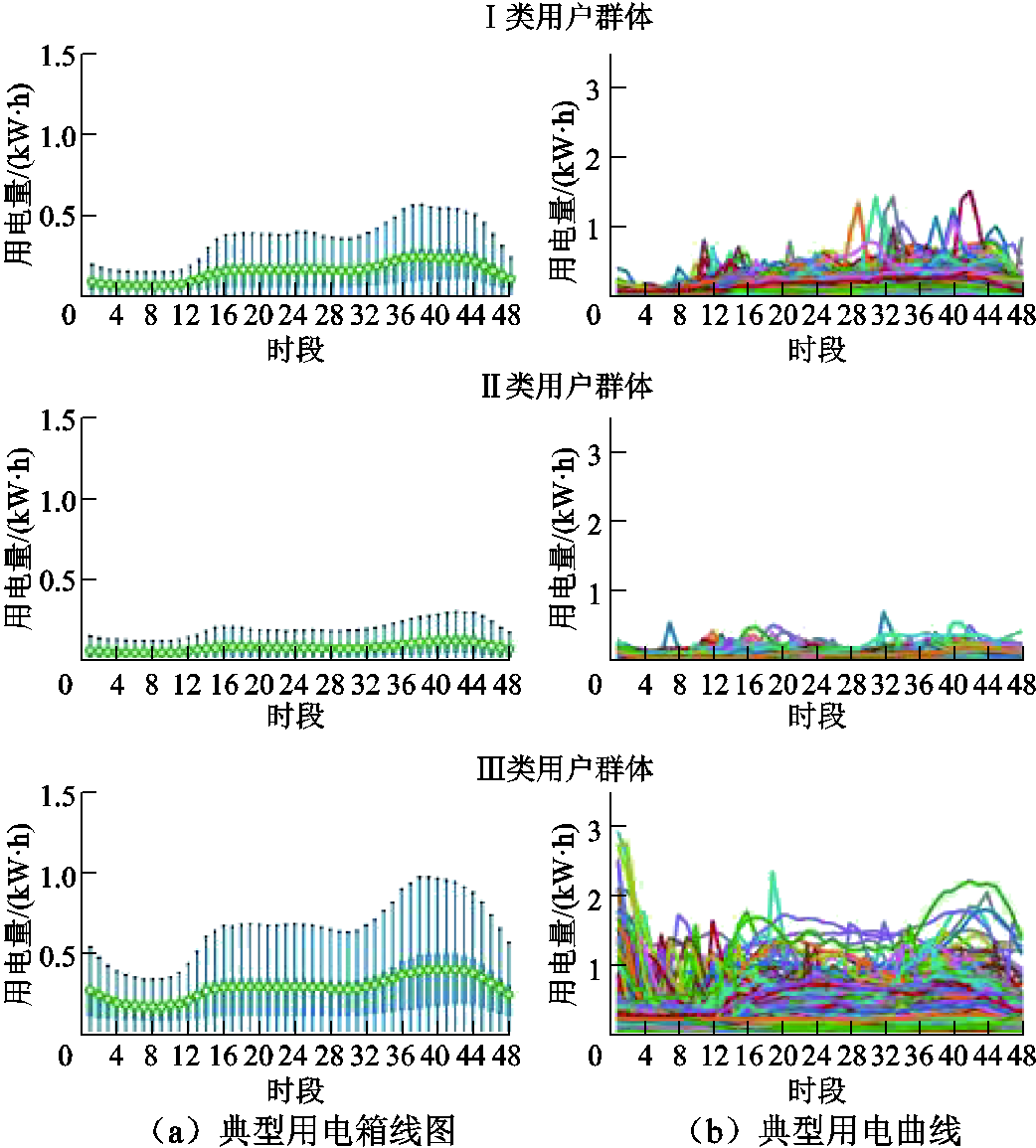
图5 数据集1各类用户典型用电箱线图与曲线图
Fig.5 Typical power consumption box diagram and curve diagram of various users in Dataset 1
由图5a可知，对于数据集1，在用电量消耗大小层面，Ⅱ类用户群体用电消耗量较小，各个时段的用电消耗量均值均未超过0.25kW·h；第Ⅰ类用户群体用电消耗量中等，各个时段的用电消耗量均值处在0.25kW·h左右；Ⅲ类用户群体用电消耗量较高，各个时段用电消耗量均值基本都大于0.25kW·h。由图5b可知，在用电能耗变化趋势层面，Ⅰ类与Ⅱ类用户群体用电曲线波动性较小，变化较为规律，Ⅲ类用户群体用电曲线波动性大。Ⅰ类和Ⅲ类用户群体在时段12～20存在小的用电高峰，在时段36～44存在大的用电高峰，整体呈现双峰型用电曲线；对于Ⅲ类用户群体，部分用户的用电高峰出现在时段0～4。
数据集2中每类用户的典型用电箱线图与典型用电曲线如附图2所示。对于数据集2，由附图2a可知，在用电量消耗大小层面，Ⅰ类用户群体在各个时段用电量均值大，Ⅱ类与Ⅲ类用户群体用电量消耗均值小。由附图2b可知，在用电能耗变化趋势层面，Ⅱ类与Ⅲ类用户群体的用电曲线波动性小，Ⅰ类用户群体的用电曲线波动性大。所有三类用户群体整体都呈现双峰型用电曲线，类似于数据集1，在时段16～20与时段36～44出现用电高峰，并且Ⅰ类用户群体在时段0～4的用电量消耗也处于较高水平。
为验证本文模型所提取的低维用电特征向量具有良好的用户区分度，利用t分布随机近邻嵌入（t-distributed Stochastic Neighbor Embedding, t-SNE）算法将所提取的特征向量降至2维，并结合散点图对其进行可视化。t-SNE是一种强大的高维数据降维方法，相比于其他降维算法，其主要优势为可保持数据的局部结构与全局结构[26]。将降至2维后的数据分别命名为X1和X2。对数据集1所提取的特征向量降维后散点图如图6所示。
图6 数据集1特征向量降维后散点图
Fig.6 Feature vector scatter plot after dimensionality reduction of Dataset 1
数据集2特征向量降维后散点图如附图3所示。通过图6和附图3可以发现，各类用户的特征向量数据经过t-SNE降维后具有明显的区分度，同类别用户明显属于同一簇，不同类用户之间的簇界限明显。
4.2.2 动态电价用户分类结果分析
对于动态电价用户，类似地，数据集3中每类用户的典型用电箱线图与典型用电曲线如图7所示。数据集4每类用户的典型用电箱线图与典型用电曲线如附图4所示。由图7和附图4可知，对于数据集3，在用电量消耗大小层面，Ⅱ类用户群体用电量消耗水平较低；Ⅲ类用户群体用电量水平中等，整体均值在0.25～0.5kW·h左右；相比于以上两类，Ⅰ类用户群体用电量大小水平高，整体均值为0.5kW·h。对于数据集4，Ⅰ类、Ⅱ类、Ⅲ类用户群体的用电量大小水平分别呈低、高、中变化，整体均值水平分别在0.2kW·h、0.5kW·h、0.3kW·h左右。在用电能耗变化趋势层面，数据集3和数据集4的各个类别的用户群体具有大致相似的用电行为特性，在时段12～16存在用电量消耗攀升的过程，并且在时段16～32的消耗趋于平缓，时段32～40再次出现用电消耗高峰，往后的剩余时段用电量消耗逐渐下降并趋于平缓。
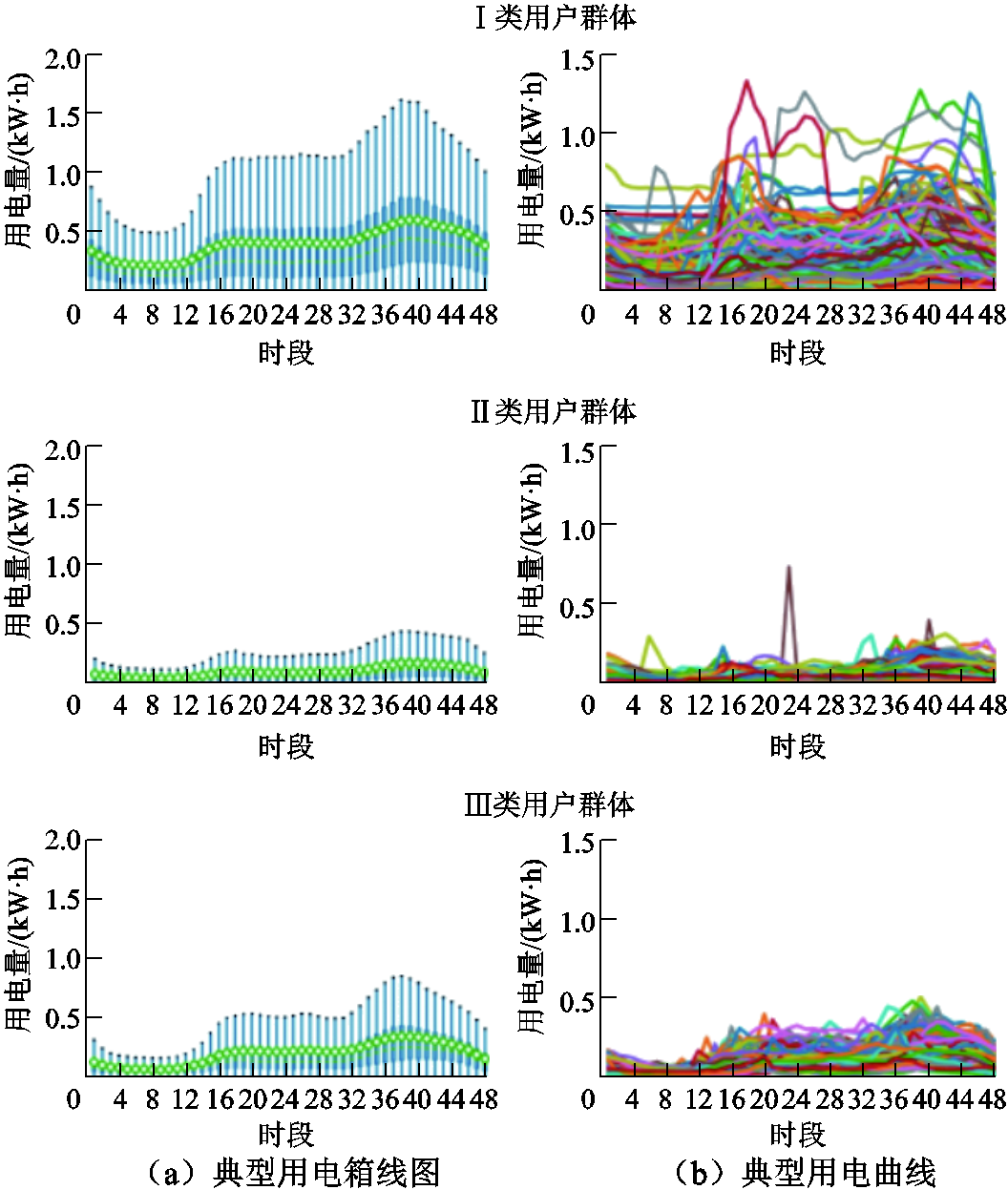
图7 数据集3各类用户典型用电箱线图与曲线图
Fig.7 Typical power consumption box diagram and curve diagram of various users in Dataset 3
对数据集3提取的特征向量降维后可视化散点图如图8所示。数据集4特征向量降维后散点图如附图5所示。由图8和附图5可知，对动态电价用户数据集所提取的特征向量，经t-SNE降维并可视化后，相同类别的用户聚于同一簇，不同类别的用户群体之间的界限明显。
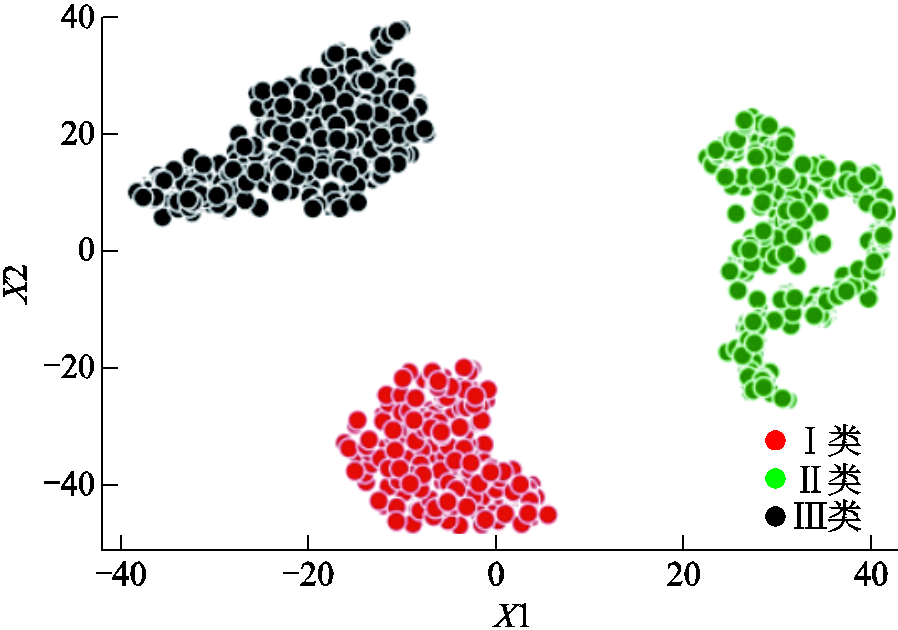
图8 数据集3特征向量降维后散点图
Fig.8 Feature vector scatter plot after dimensionality reduction of Dataset 3
由于动态电价用户实行阶梯电价，用户会根据实时电价的变化情况选择是否参与电价激励响应。为验证用户分类结果在评估用户负荷调控潜力中的应用，在动态电价用户分类结果的基础上，根据动态电价信息选择典型的电价变化日期，对不同类型用户群体的典型用电曲线进行对比。对于数据集3，本文选取间隔较近的日期2013-12-18与2013-12-22作对比，这两日为间隔较近的日期，所以用户用电量需求不会发生大的改变，其中12月18日各个时段均为正常电价，12月22日各时段的电价类型不同，包含高、正常、低水平电价，为阶梯电价。分别对各个类别用户群体的用电序列在各个时刻取均值，得到该类用户的典型用电曲线，具体对比如图9所示。
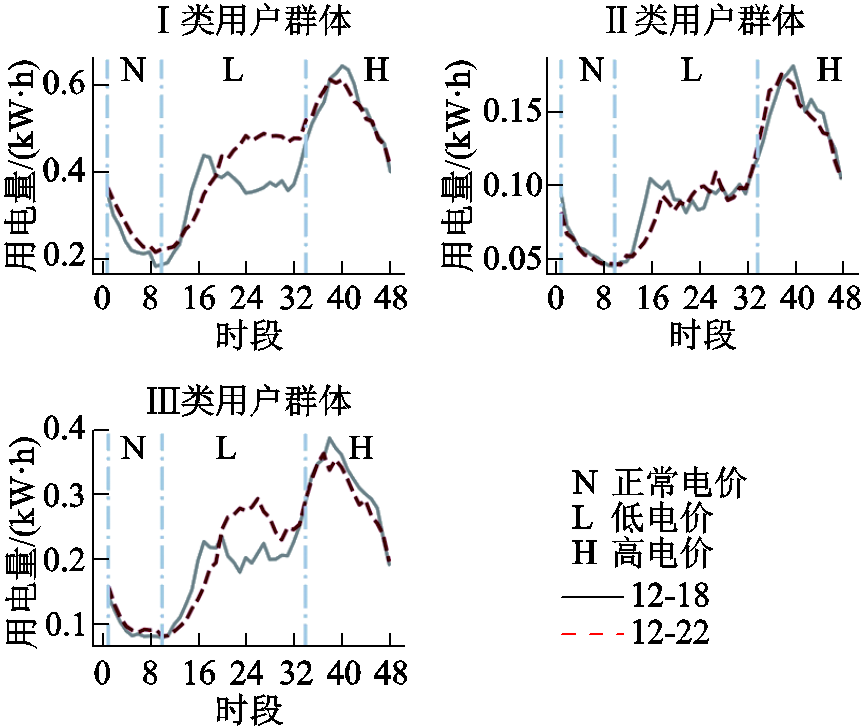
图9 数据集3各类用户不同电价下用电曲线对比
Fig.9 Comparison of electricity consumption curves of various users in Dataset 3 under different electricity prices
在图9中，不同区间代表所实行动态电价的不同电价水平，可以发现不同类别的用户群体对电价激励响应情况不相同。Ⅰ类和Ⅲ类用户群体明显地参与电价激励响应，相比于12月18日各时段只实行正常电价时的典型用电曲线，这些用户群体在12月22日的低电价时段大幅增加了用电量，Ⅱ类用户群体对电价激励响应并不积极，未明显改变自身的用电行为。在高电价时段，各类用户群体基本均未改变自身的用电习惯。
对于数据集4，选择2013-7-22与2013-7-23作为对比日期，其中7月22日的各时段电价不发生变化，均为正常电价，7月23日的不同时段电价类型不同，为阶梯电价。具体对比如附图6所示，Ⅰ类和Ⅲ类用户群体对电价激励进行响应，在低电价时段适当增加了自身的用电量，Ⅱ类用户群体未明显改变自身的用电行为。考虑数据集4所在日期的平均温度相比于数据集3较高，用户的制热负荷少，所以在用户群体参与电价激励响应时所改变的用电量较少。
为了验证本文所提出模型的优越性，引入PCA-Kmeans聚类方法、PCA-层次聚类法及先用CNN-AE特征提取再单独聚类的非联合模型方法进行对比。同时为更全面地评价各类方法的优劣，另引入DBI（Davies-Bouldin Index）指标以及CH（Calinski-Harabas）指标。
DBI指标衡量同一簇中数据的紧密性,其值越小代表分类效果越好，其计算公式为
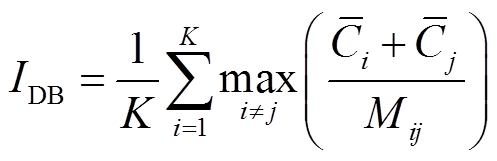（19）
式中，
与
分别为第i类和第j类所有样本到其所属类中心距离的平均值；Mij为不同类别的类中心距离；K为聚类数量。
CH指标通过计算类内各点与类中心的距离二次方和来度量类内的紧密度，其值越大代表类内自身越紧密，类与类之间越分散，即聚类结果更优。
结合SC指标、DBI指标和CH指标，计算各方法在聚类数为3时对应的指标值，结果见表2。
表2 PCA-Kmeans、PCA-层次聚类法、非联合模型和联合模型算法性能对比
Tab.2 Performance comparison among PCA-Kmeans, PCA hierarchical clustering, non-joint model, joint model
数据集PCA-KmeansPCA-层次聚类法非联合模型本文方法 SCDBICHSCDBICHSCDBICHSCDBICH 10.2891.9281 233.10.4121.3931 590.80.2411.3102 138.00.7320.4775 907.4 20.2282.1141 135.70.4171.3421 395.40.3941.2651 938.50.7430.4885 316.7 30.2491.976466.730.3081.263412.950.3430.997950.180.5500.3711 456.7 40.2022.282343.690.3211.352359.240.3960.919835.310.5770.3981 213.8
由表2可知，本文所提出的联合模型与其余算法相比，SC指标更高，DBI值更小，CH值更高，分类效果更好。非联合模型相比基于PCA降维的分类方法各指标提升效果不大，然而采用多任务学习的联合模型对分类有效性提升明显。
为了进一步验证本文方法的适用性，本文另在爱尔兰CER公开数据集上选取700名固定电价居民用户进行了方法验证[27]，算例仿真结果如附图7、附图8和附表1所示。经验证，本文方法在CER数据集上具有一定优越性。
针对居民用户用电数据的海量高维性以及非线性关系难以提取问题，本文提出一种基于CNN-AE与层次聚类联合模型的居民用电模式分类方法，并以实际公开数据集为例，验证了本文所提分类方法的有效性。算例结果表明：
1）考虑温度因素和用户电价类型，分时段、分类型对用户进行划分，可对用户进行更加精细化的分类。
2）利用本文模型所提取的居民用户用电特征向量具有良好的用户区分度。
3）与所引入的其他算法对比，本文所提算法模型在多个聚类有效性指标上表现更佳，具备明显优势。
4）对于动态电价用户，利用本文所提算法模型可以有效挖掘用电行为变化特性，进行合理分类，可为负荷调控、实时电价制定提供理论支撑。
假设X是一个离散型随机变量，其取值集合为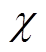
，概率分布函数
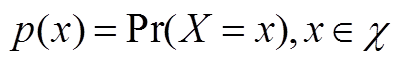,，则定义事件X=x0的信息量为
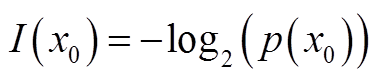
信息量的期望称为熵，假设事件X共有n种可能，发生事件xi的概率为p(xi),则该事件的熵H(X)为
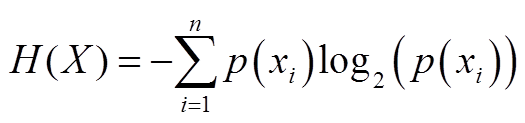
KL散度又称为相对熵,如果对于同一个随机变量x有两个单独的概率分布p(x)和q(x)，可以使用KL散度来衡量这两个分布的差异，计算公式为
式中，p为样本的真实分布；q为模型所预测的分布。
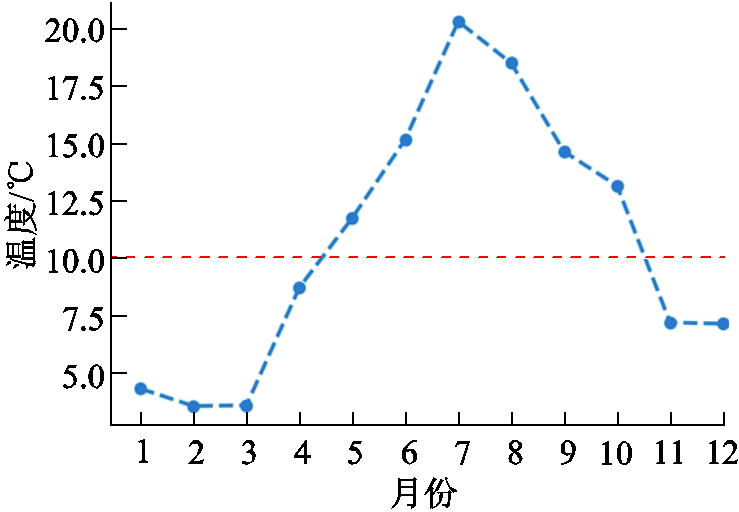
附图1 2013年伦敦月平均温度
App.Fig.1 Average monthly temperature in London in 2013
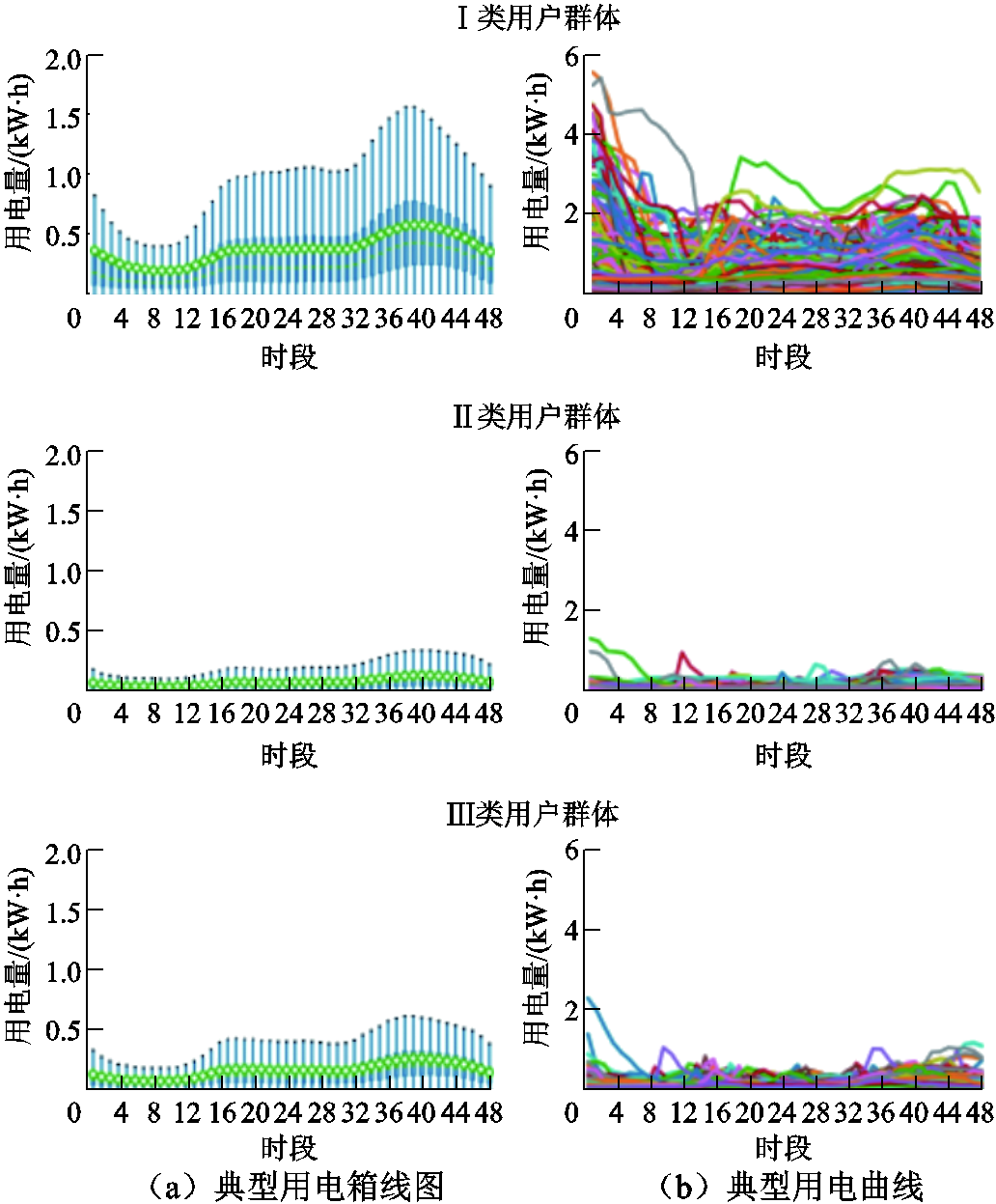
附图2 数据集2各类用户用电箱线图与用电曲线图
App.Fig.2 Typical power consumption box diagram and curve diagram of various users in Dataset 2
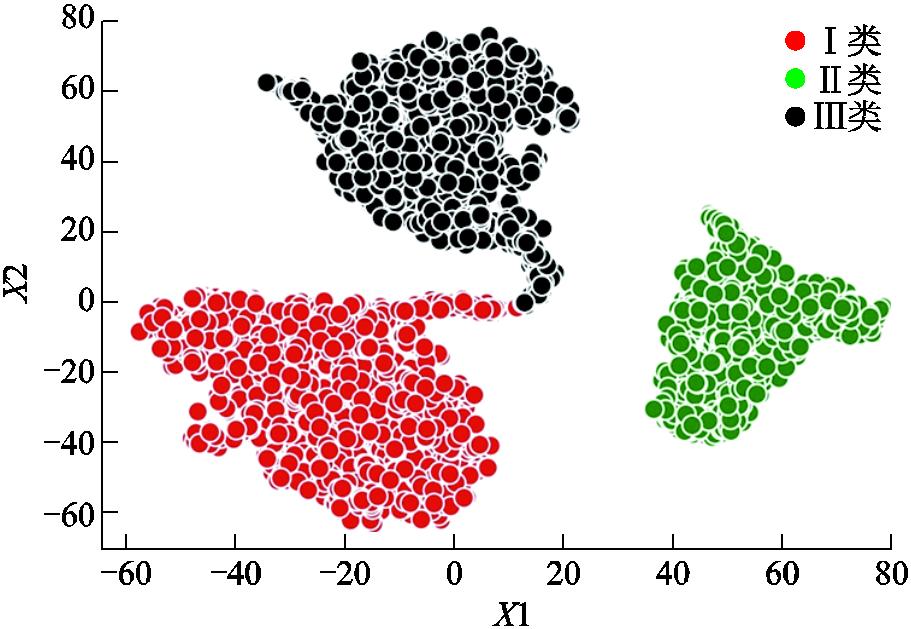
附图3 数据集2特征向量降维后散点图
App.Fig.3 Feature vector scatter plot after dimensionality reduction of Dataset 2
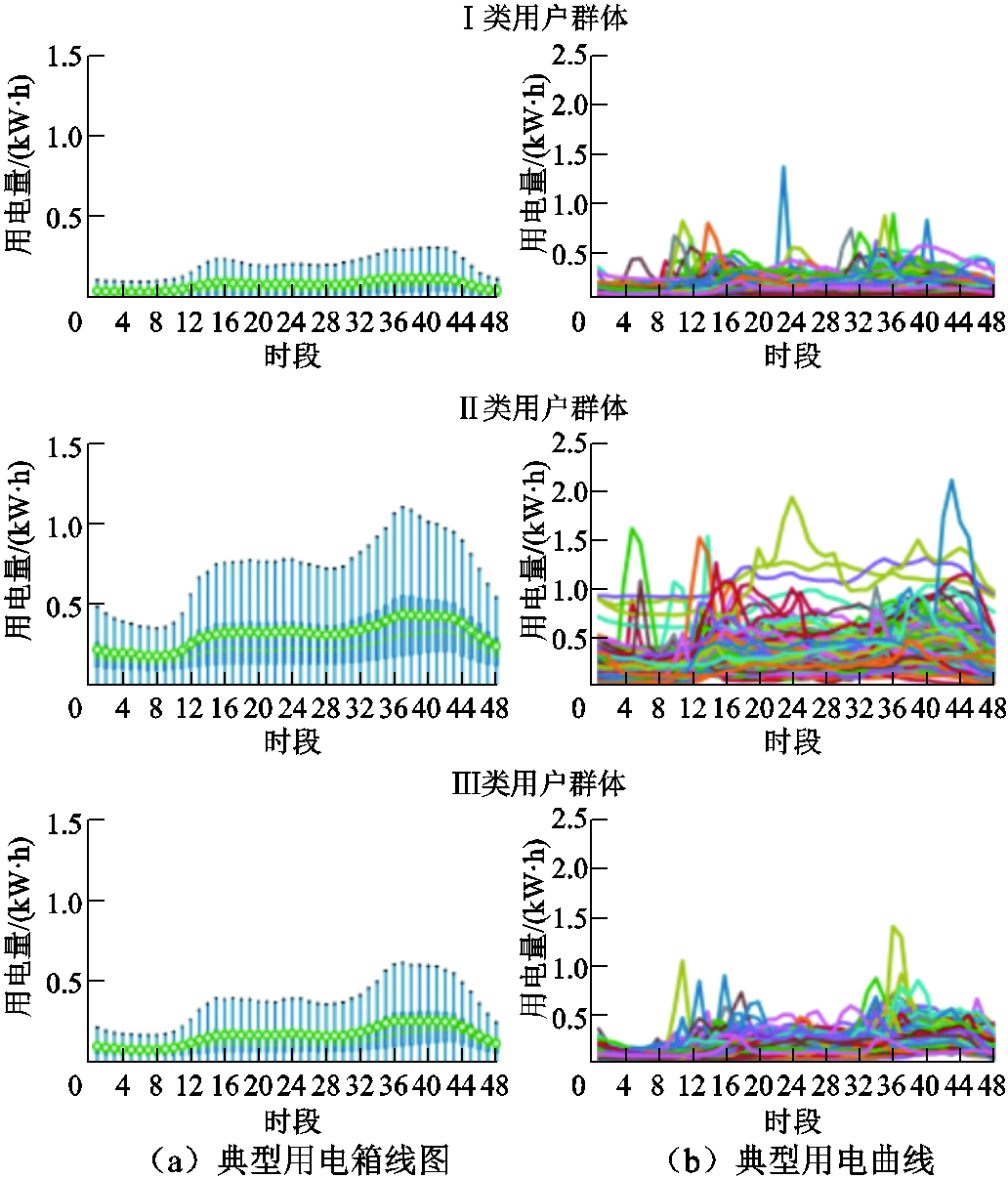
附图4 数据集4各类用户的典型用电箱线图与曲线图
App.Fig.4 Typical power consumption box diagram and curve diagram of various users in Dataset 4
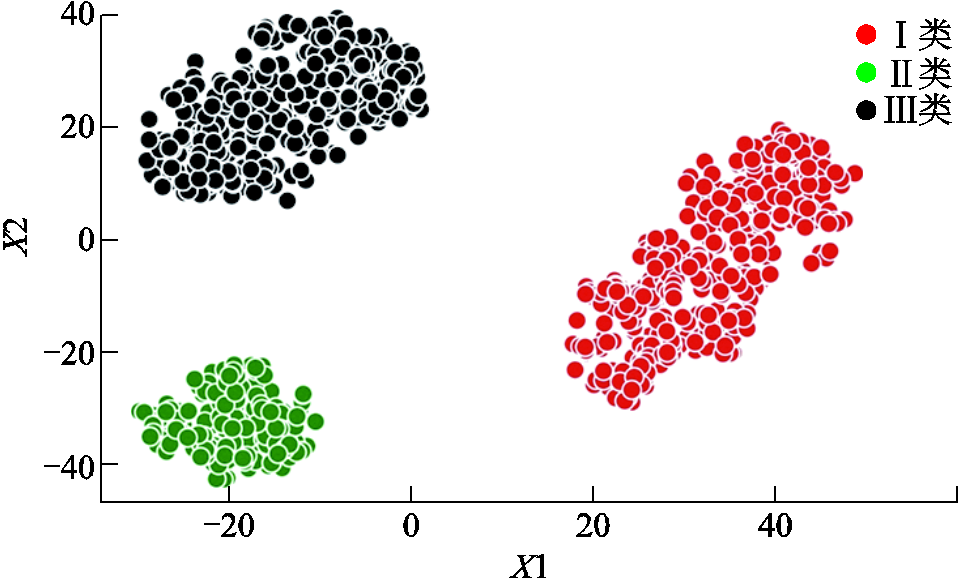
附图5 数据集4特征向量降维后散点图
App.Fig.5 Feature vector scatter plot after dimensionality reduction of Dataset 4
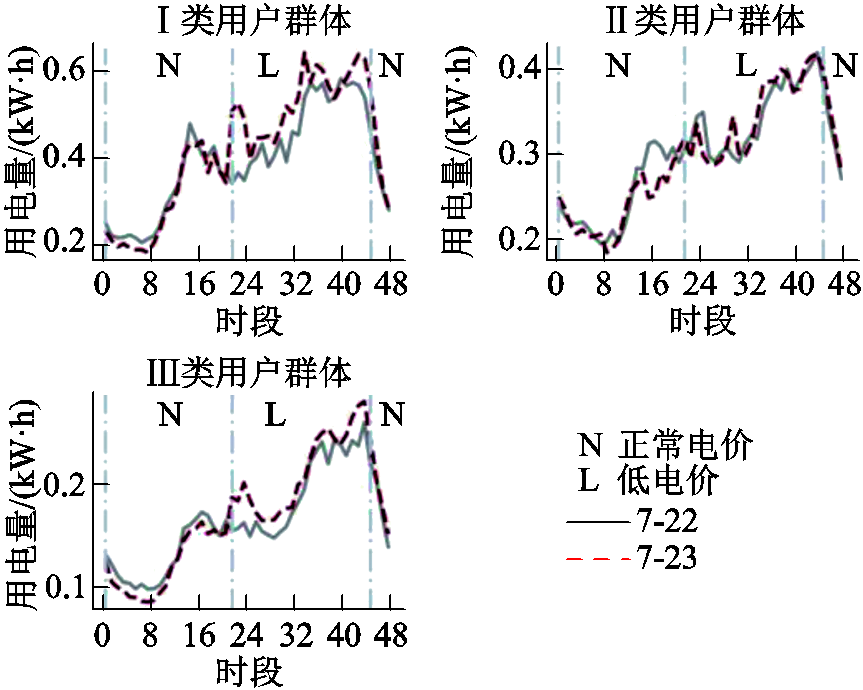
附图6 数据集4各类用户不同电价下用电曲线对比
App.Fig.6 Comparison of electricity consumption curves of various users in Dataset 4 under different electricity prices
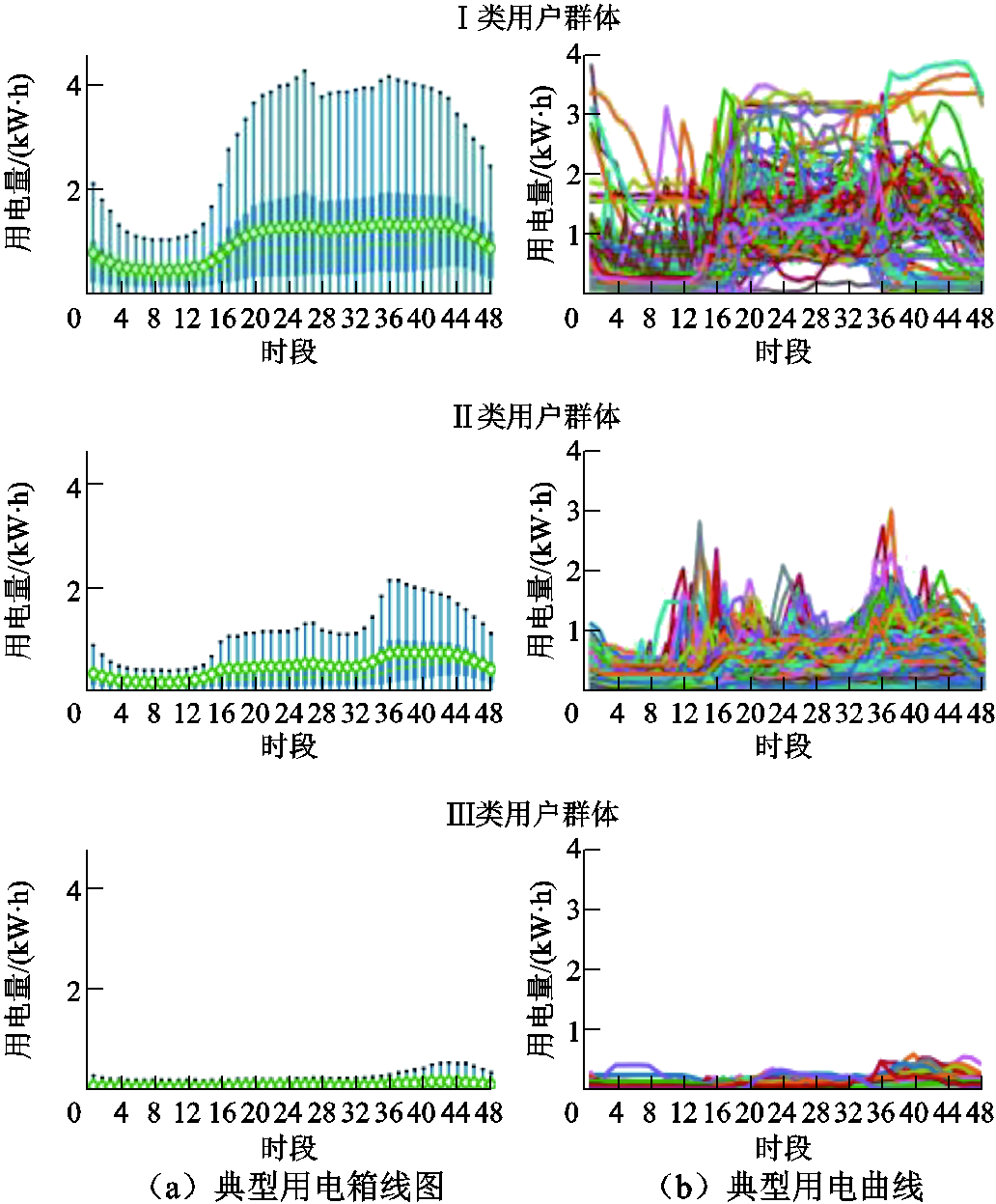
附图7 CER数据集各类用户典型用电箱线图与用电曲线
App.Fig.7 Typical power consumption box diagram and curve diagram of various users in Dataset CER
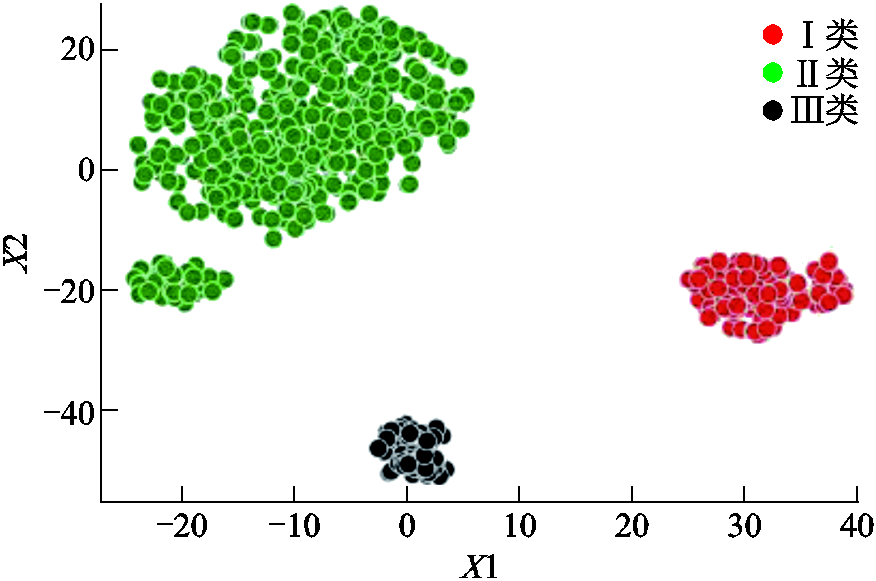
附图8 CER数据集特征向量降维后散点图
App.Fig.8 Feature vector scatter plot after dimensionality reduction of Dataset CER
附表1 CER数据集各算法性能对比
App.Tab.1 Performance comparison of various algorithms in Dataset CER
对比指标PCA-KmeansPCA-层次聚类法非联合模型本文模型 SC0.163 20.275 90.507 70.854 2 DBI1.788 11.426 41.160 70.811 2 CH105.41221.17389.02631.72
参考文献
[1] 雷怡琴, 孙兆龙, 叶志浩, 等. 电力系统负荷非侵入式监测方法研究[J]. 电工技术学报, 2021, 36(11): 2288-2297.
Lei Yiqin, Sun Zhaolong, Ye Zhihao, et al. Research on non-invasive load monitoring method in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2288-2297.
[2] Wang Yi, Chen Qixin, Hong Tao, et al. Review of smart meter data analytics: applications, methodologies, and challenges[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 3125-3148.
[3] 王孝慈, 董树锋, 王莉, 等. 基于电器状态关联分析的民可平移负荷辨识[J]. 电工技术学报, 2020, 35(23): 4961-4970.
Wang Xiaoci, Dong Shufeng, Wang Li, et al. Resident shiftable loads monitoring based on load states set correlation analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4961-4970.
[4] 周东国, 张恒, 周洪, 等. 基于状态特征聚类的非侵入式负荷事件检测方法[J]. 电工技术学报, 2020, 35(21): 4565-4575.
Zhou Dongguo, Zhang Heng, Zhou Hong, et al. Non-intrusive load event detection method based on state feature clustering[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4565-4575.
[5] 涂青宇, 苗世洪, 张迪, 等. 分布式发电市场化环境下基于价格型需求响应的农村光伏交易模式研究[J]. 电工技术学报, 2020, 35(22): 4784-4797.
Tu Qingyu, Miao Shihong, Zhang Di, et al. Research on rural photovoltaic trading pattern based on price-based demand response under marketization environment of distributed generation[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4784-4797.
[6] Kong Weicong, Dong Zhaoyang, Jia Youwei, et al. Short-term residential load forecasting based on LSTM recurrent neural network[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 841-851.
[7] 王帅, 杜欣慧, 姚宏民, 等. 面向含多种用户类型的负荷曲线聚类研究[J]. 电网技术, 2018, 42(10): 3401-3412.
Wang Shuai, Du Xinhui, Yao Hongmin, et al. Research on load curve clustering with multiple user types[J]. Power System Technology, 2018, 42(10): 3401-3412.
[8] 王毅, 张宁, 康重庆, 等. 电力用户行为模型: 基本概念与研究框架[J]. 电工技术学报, 2019, 34(10): 2056-2068.
Wang Yi, Zhang Ning, Kang Chongqing, et al. Electrical consumer behavior model: basic concept and research framework[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2056-2068.
[9] 徐磊, 杨秀, 张美霞. 基于数据挖掘的工业用户用电行为分析[J]. 电测与仪表, 2017, 54(16): 68-74.
Xu Lei, Yang Xiu, Zhang Meixia. Industrial users of electricity behavior analysis based on data mining[J]. Electrical Measurement ＆ Instrumentation, 2017, 54(16): 68-74.
[10] 李欣然, 姜学皎, 钱军, 等. 基于用户日负荷曲线的用电行业分类与综合方法[J]. 电力系统自动化, 2010, 34(10): 56-61.
Li Xinran, Jiang Xuejiao, Qian Jun, et al. A classifying and synthesizing method of power consumer industry based on the daily load profile[J]. Automation of Electric Power Systems, 2010, 34(10): 56-61.
[11] 杨浩, 张磊, 何潜, 等. 基于自适应模糊C均值算法的电力负荷分类研究[J]. 电力系统保护与控制, 2010, 38(16): 111-115, 122.
Yang Hao, Zhang Lei, He Qian, et al. Study of power load classification based on adaptive fuzzy C means[J]. Power System Protection and Control, 2010, 38(16): 111-115, 122.
[12] Benítez I, Quijano A, Díez J L, et al. Dynamic clustering segmentation applied to load profiles of energy consumption from Spanish customers[J]. International Journal of Electrical Power & Energy Systems, 2014, 55: 437-448.
[13] 金伟超, 张旭, 刘晟源, 等. 基于剪枝策略和密度峰值聚类的行业典型负荷曲线辨识[J]. 电力系统自动化, 2021, 45(4): 20-28.
Jin Weichao, Zhang Xu, Liu Shengyuan, et al. Identification of typical industrial power load curves based on pruning strategy and density peak clustering[J]. Automation of Electric Power Systems, 2021, 45(4): 20-28.
[14] 赵晋泉, 夏雪, 刘子文, 等. 电力用户用电特征选择与行为画像[J]. 电网技术, 2020, 44(9): 3488-3496.
Zhao Jinquan, Xia Xue, Liu Ziwen, et al. User electricity consumption feature selection and behavioral portrait[J]. Power System Technology, 2020, 44(9): 3488-3496.
[15] Haben S, Singleton C, Grindrod P. Analysis and clustering of residential customers energy behavioral demand using smart meter data[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 136-144.
[16] 王潇笛, 刘俊勇, 刘友波, 等. 采用自适应分段聚合近似的典型负荷曲线形态聚类算法[J]. 电力系统自动化, 2019, 43(1): 110-118.
Wang Xiaodi, Liu Junyong, Liu Youbo, et al. Shape clustering algorithm of typical load curves based on adaptive piecewise aggregate approximation[J]. Automation of Electric Power Systems, 2019, 43(1): 110-118.
[17] 徐春华, 陈克绪, 马建, 等. 基于深度置信网络的电力负荷识别[J]. 电工技术学报, 2019, 34(19): 4135-4142.
Xu Chunhua, Chen Kexu, Ma Jian, et al. Recognition of power loads based on deep belief network[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4135-4142.
[18] Wang Yi, Chen Qixin, Kang Chongqing, et al. Clustering of electricity consumption behavior dynamics toward big data applications[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2437-2447.
[19] 孙毅, 毛烨华, 李泽坤, 等. 面向电力大数据的用户负荷特性和可调节潜力综合聚类方法[J]. 中国电机工程学报, 2021, 41(18): 6259-6271.
Sun Yi, Mao Yehua, Li Zekun, et al. A comprehensive clustering method of user load characteristics and adjustable potential based on power big data[J]. Proceedings of the CSEE, 2021, 41(18): 6259-6271.
[20] 庞传军, 余建明, 冯长有, 等. 基于LSTM自动编码器的电力负荷聚类建模及特性分析[J]. 电力系统自动化, 2020, 44(23): 57-63.
Pang Chuanjun, Yu Jianming, Feng Changyou, et al. Clustering modeling and characteristic analysis of power load based on long-short-term-memory auto-encoder[J]. Automation of Electric Power Systems, 2020, 44(23): 57-63.
[21] 卢锦玲, 郭鲁豫. 基于改进深度残差收缩网络的电力系统暂态稳定评估[J]. 电工技术学报, 2021, 36(11): 2233-2244.
Lu Jinling, Guo Luyu. Power system transient stability assessment based on improved deep residual shrinkage network[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2233-2244.
[22] 张斌, 庄池杰, 胡军, 等. 结合降维技术的电力负荷曲线集成聚类算法[J]. 中国电机工程学报, 2015, 35(15): 3741-3749.
Zhang Bin, Zhuang Chijie, Hu Jun, et al. Ensemble clustering algorithm combined with dimension reduction techniques for power load profiles[J]. Proceedings of the CSEE, 2015, 35(15): 3741-3749.
[23] Xie Junyuan, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis[EB/OL]. 2015, arXiv: 1511.06335. https://arxiv.org/abs/1511.06335.
[24] London Government. Smart meter energy use data in London households[DB/OL]. [2015-09-26]. https:// old.datahub.io/dataset/smartmeter-energy-use-data-in- london-households.
[25] Alonso A M, Nogales F J, Ruiz C. Hierarchical clustering for smart meter electricity loads based on quantile autocovariances[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 4522-4530.
[26] Van Der Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9: 2579-2625.
[27] Commission for Energy Regulation. CER smart metering project[DB/OL]. [2012-03-01]. https://www.ucd.ie/ issda /data/commissionforenergyregulationcer/.
Residential Electricity Consumption Pattern Classification Method Based on Multi-Task Joint Model
Abstract Identifying the electricity consumption behavior patterns of massive residential users and then making a reasonable classification, can provide auxiliary decision-making for demand-side lean management. This paper proposes a method of residential electricity consumption pattern classification based on a multi-task joint model of convolutional neural network auto-encoder(CNN-AE) and hierarchical clustering. Firstly, a method for filling missing values based on the mean value of simultaneous measurement data and an outlier detection method based on seasonal hybrid extreme studentized deviate test, were proposed to clean and correct massive and high-dimensional electricity data. Secondly, the CNN-AE was used to extract the features of the residential electricity consumption data, and obtained the feature vector which could characterize the residents' electricity consumption behavior. Then, combining the hierarchical clustering algorithm and silhouette coefficient to determine the number of users' cluster and each cluster centers' vector, initialized the neural network layer for user clustering with cluster centers' vector; and joined the feature extraction process and user clustering process to form a multi-task learning neural network. This network was used to achieve end-to-end classification of residential electricity consumption patterns. Finally, considering environmental temperature and electricity price factors, the proposed method was verified on actual dataset.
Keywords：Residential load, load clustering, convolutional neural network, auto-encoder, joint model
DOI:10.19595/j.cnki.1000-6753.tces.210763
中图分类号：TM769; TP193
国家重点专项（2020YFB1506804）、国家自然科学基金（51907114）和上海市教育发展基金会晨光计划（19CG61）资助项目。
收稿日期 2021-05-27
改稿日期 2021-09-13
徐明杰 男，1997年生，硕士研究生，研究方向为电力大数据。E-mail：xmj36@foxmail.com
赵 健 男，1990年生，副教授，研究方向为中压配电网精益化管理，图像处理、自然语言处理技术在电力系统运营管理中的应用等。E-mail：zhaojianee@foxmail.com（通信作者）
（编辑 赫蕾）