
图1 全过程恢复问题基本框图
Fig.1 Basic diagram of the whole process power system restoration decision
摘要 我国能源低碳转型过程中电力系统的风电接入比例将不断提高,研究新形势下的恢复控制问题对提升电力系统的保底安全性具有重要意义。针对风电接入背景下的电力系统恢复决策优化问题,该文建立了考虑风电不确定性的全过程两阶段鲁棒优化模型。第一阶段考虑已恢复节点重要度指标、负荷恢复量以及风功率波动场景集,对系统元件恢复次序做出决策;第二阶段包含双层目标,外层目标为最大化风功率波动对系统负荷恢复量的影响,内层目标为在最恶劣的风电波动场景下最大化系统负荷恢复量,并利用对偶原理将第二阶段问题转化为单层优化问题。采用区间不确定集描述风功率时空不确定性,通过列与约束生成算法求解此两阶段优化问题,利用启发式方法加速主问题求解。最后,通过新英格兰39节点系统与实际电网算例验证所提方法的鲁棒性与实用性。
关键词:大停电 恢复控制 全过程 鲁棒优化 列与约束生成
双碳背景下,未来电网将逐步成为新能源主导的新型电力系统。然而,新能源的高比例接入将使系统面临一些额外的停电风险,如南澳“9.28”大停电[1]、英国“8.9”大停电事故[2]、德州“2.15”大停电[3]等。因此研究如何利用以风电为代表的新能源资源来制定安全、高效的系统恢复方案,对于提高我国低碳转型过程中系统广义安全防御能力、缩短系统恢复时间、加快系统恢复进程具有重要意义。
一般而言,大停电后根据系统恢复过程中不同时期、不同阶段的主要矛盾,可将系统恢复进程划分为黑启动、网架重构以及负荷恢复三个阶段[4],已有研究探索了风电在参与上述三个阶段系统恢复进程中的作用。在黑启动阶段,文献[5]提出一种使风电场具备黑启动能力的储能优化配置方法;文献[6]协调风光储系统,采用模型预测控制技术,构建了风光储发电系统作为黑启动电源的滚动优化模型。在网架重构阶段,文献[7]采用信息间隙决策理论(Information Gap Decision Theory, IGDT)刻画风电出力的不确定性,并制定相应的网架重构恢复方案;文献[8]提出一种考虑多风电场黑启动价值的机组恢复顺序双层优化决策方法。在负荷恢复阶段,文献[9]基于条件风险价值理论,建立了负荷恢复风险价值与恢复时间的双目标双层优化模型;文献[10]考虑风电预测误差相关性,建立负荷恢复两阶段鲁棒优化恢复模型。
已有研究多集中于黑启动、网架重构和负荷恢复三个阶段以及源网荷不同恢复主体的独立优化建模与求解,例如单独研究网架重构阶段的机组起动顺序优化[11]、网架重构阶段确立目标网架[12]、负荷恢复阶段的投负荷方案[9],缺乏对于恢复过程不同阶段、不同恢复主体的统一建模。而大停电后的系统恢复准备阶段,往往涉及众多恢复主体及不同恢复时步之间的协调统筹,调控中心有必要基于系统当前状态对未来若干时步的恢复操作做一全过程的恢复计划(Restoration Planning, RP)[13-14]。
系统恢复方案全过程优化的每一步恢复操作都把前一步决策结果作为参考,前后恢复决策相互耦合。针对规模风电接入的全过程恢复决策问题,文献[14]基于风电出力典型场景,建立基于全过程恢复思想的随机优化模型,并通过L形算法求解。然而,恢复进程中系统尚未成型,具有较弱的风险抵御能力,应用随机优化方法所得全过程恢复方案并不能保证适应于极端风电波动场景,因此有必要通过鲁棒优化寻求风电不确定条件下的系统全过程恢复方案。现有鲁棒优化模型的求解算法包括Benders割生成算法[15]、列与约束生成(Column-and-Constraint Generation, C&CG)算法[16-18]等。Benders割生成算法依赖于对偶信息的反馈,而列与约束生成算法不需要对偶信息反馈,只需极端场景的生成,因此在求解某些类型问题上具有收敛速度快等优势。
鉴于此,本文基于全过程恢复思想,考虑系统恢复进程中风功率的时空不确定性,建立以已恢复节点重要度与负荷恢复效益为目标的两阶段三层鲁棒优化模型,采用并行启发式与C&CG方法对优化模型迭代求解,最后通过新英格兰10机39节点系统与某实际系统算例进行验证。
全过程恢复计划可以划分为两个阶段[14]:第一阶段为元件恢复次序决策,用以指导并协调各恢复主体的恢复次序,例如省调向各省属厂站、地调部门下达何时恢复指令,地调部门向各厂站、县调部门下达何时恢复指令等,以便各恢复主体能够提前协调并做好恢复前的准备工作;第二阶段基于第一阶段元件恢复次序决策结果及风功率波动场景得到具体的厂站恢复方案。全过程恢复问题的基本框图如图1所示。需要注意,本文全过程两阶段鲁棒恢复模型重点研究适应于极端风电波动场景的元件恢复次序决策,通过求解第二阶段问题生成极端风电波动场景反馈回第一阶段,反复迭代后最终确定元件恢复次序及时间。

图1 全过程恢复问题基本框图
Fig.1 Basic diagram of the whole process power system restoration decision
电力系统恢复通常要求在尽可能短的时间内高效地恢复全网负荷,同时兼顾各种恢复效益[19-20]。本文以负荷恢复量以及恢复过程中关键节点的恢复情况作为优化模型的寻优指标,目标函数为
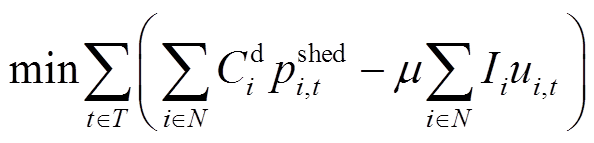 (1)
(1)
式中,T、N分别为恢复时步集合、系统母线集合;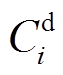 为待恢复负荷重要性权重系数;
为待恢复负荷重要性权重系数;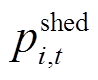 为母线i在t时步未恢复负荷量;Ii为母线i的节点重要度;ui,t表示t时步母线i是否被恢复,ui,t=1为t时步母线i被恢复,反之则未被恢复;μ为系统恢复效益中节点重要度的权重系数,一般由恢复决策者视情况而定。
为母线i在t时步未恢复负荷量;Ii为母线i的节点重要度;ui,t表示t时步母线i是否被恢复,ui,t=1为t时步母线i被恢复,反之则未被恢复;μ为系统恢复效益中节点重要度的权重系数,一般由恢复决策者视情况而定。
考虑风功率波动的电力系统全过程恢复可以建模为三层两阶段鲁棒模型。第一层(第一阶段)决定电力系统元件的恢复顺序,包括发电机的起动顺序、母线和线路的充电顺序;第二层(第二阶段)最大化风功率波动对第一阶段恢复决策的影响,通过反复迭代,确定对恢复决策影响最大的风功率波动场景集合;第三层(第二阶段)通过调整系统运行变量,在最恶劣风功率波动场景集下最小化系统失负荷量。目标函数可以重新表述为
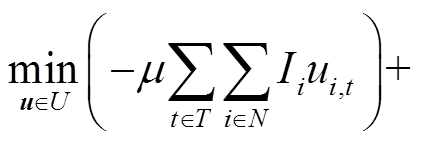
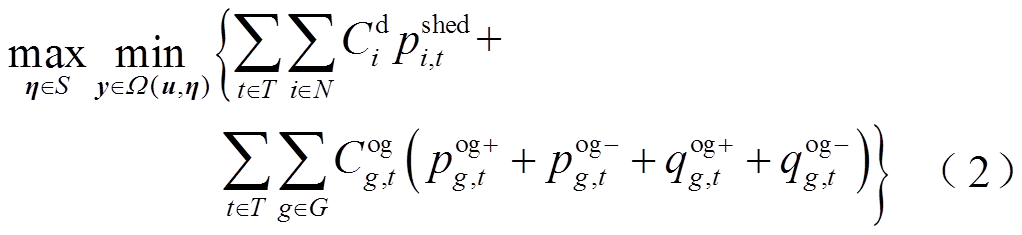
式中,G为发电机集合;U为第一层表征电力系统元件恢复顺序的决策变量集合;S为第二层不确定风功率波动场景集;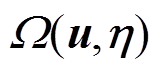 为第三层表征电力系统运行状态的变量集合,与第一层元件恢复顺序决策变量u和第二层不确定风功率波动场景η有关。考虑到恢复过程系统相对薄弱,计及风功率不确定性后可能导致特定元件恢复顺序下第二阶段的模型不可行,因此在发电机节点引入松弛量
为第三层表征电力系统运行状态的变量集合,与第一层元件恢复顺序决策变量u和第二层不确定风功率波动场景η有关。考虑到恢复过程系统相对薄弱,计及风功率不确定性后可能导致特定元件恢复顺序下第二阶段的模型不可行,因此在发电机节点引入松弛量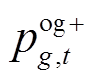 、
、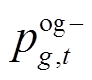 、
、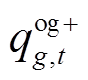 、
、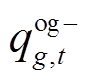 用以消除系统恢复过程中由于风功率波动造成的恢复决策不可行情况,通过设置较大的惩罚系数
用以消除系统恢复过程中由于风功率波动造成的恢复决策不可行情况,通过设置较大的惩罚系数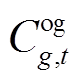 来避免求解迭代过程中问题的不可行性。其中,
来避免求解迭代过程中问题的不可行性。其中,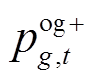 、
、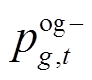 、
、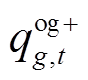 、
、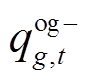 均非负。
均非负。
系统恢复决策通常会涉及到系统运行、设备操作等众多复杂的非线性约束。为减轻决策负担,相关文献在进行长时间尺度恢复决策建模时通常将潮流等稳态约束作为时步建模的主要约束[21]。本文在全过程建模时主要考虑线性化的交流潮流约束、发电机的稳态运行约束、投负荷的稳态频率约束、风功率不确定区间约束、元件恢复顺序约束等。
2.2.1 有功功率平衡约束
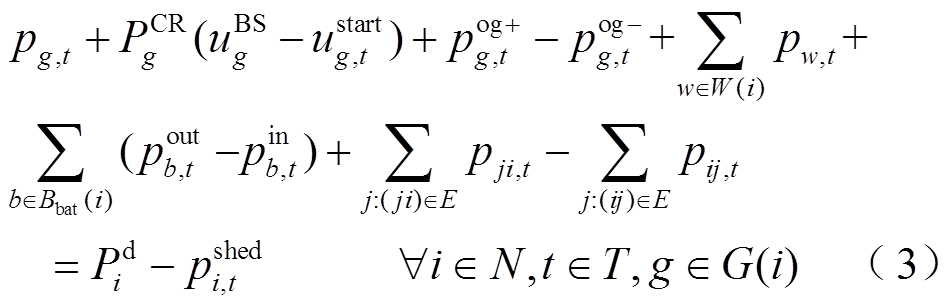
式中,W(i)、Bbat(i)、G(i)分别为与节点i相连的风电场、储能电站以及发电机集合;E为线路集合;pg,t为发电机g在时步t发出的有功功率;pw,t为风电场w在时步t发出的有功功率;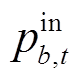 、
、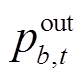 分别为时步t储能电站b的充、放电功率;
分别为时步t储能电站b的充、放电功率;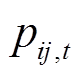 为时步t线路ij上流过的有功功率;
为时步t线路ij上流过的有功功率;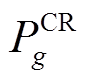 为发电机g的起动功率;
为发电机g的起动功率;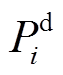 为母线i上的待恢复负荷总量;
为母线i上的待恢复负荷总量;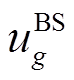 为表示机组g是否具有黑启动能力的二元参数,
为表示机组g是否具有黑启动能力的二元参数,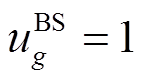 表示机组g为黑启动机组,否则为非黑启动机组;
表示机组g为黑启动机组,否则为非黑启动机组;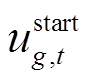 为表征机组g在时步t是否启动的二元决策变量,若
为表征机组g在时步t是否启动的二元决策变量,若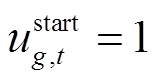 ,表示t时步机组g起动,否则不起动。
,表示t时步机组g起动,否则不起动。
2.2.2 无功功率平衡约束
系统恢复是一个动态功率恢复过程,不仅面临有功-频率调节问题,还涉及到无功-电压调控问题,因此有必要在系统恢复过程中考虑无功平衡约束。
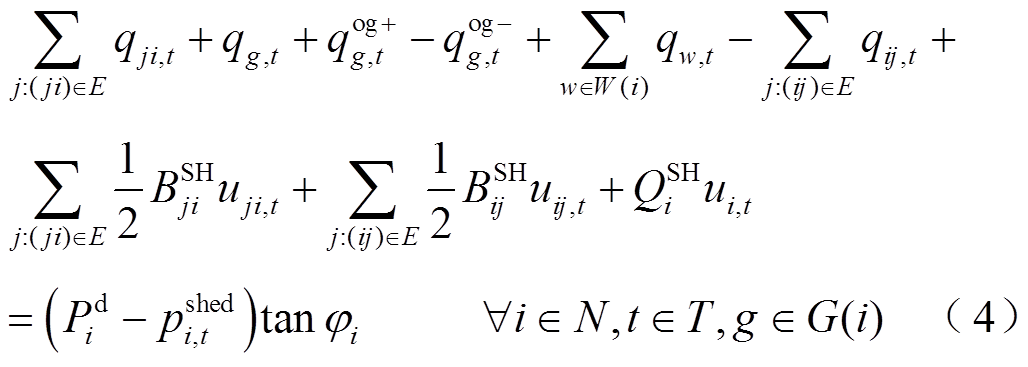
式中,qij,t为线路ij在时步t输送的无功功率;qg,t为发电机g在时步t发出的无功功率;φi为母线i处负荷的功率因数角;qw,t为风电场w在时步t发出的无功功率;uij,t表示t时步线路ij是否被恢复,uij,t=1,表示t时步线路ij被恢复,uij,t=0表示线路ij未被恢复;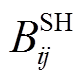 为线路ij的并联电纳;
为线路ij的并联电纳;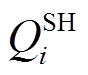 为母线i上并联电抗器提供的无功功率。
为母线i上并联电抗器提供的无功功率。
2.2.3 发电机功率约束
发电机在tstart时步起动,在ton(ton>tstart)时步并网[12],因此发电机的爬坡约束可以表示为式(5);另外发电机在ton并网后还需先爬坡到最小功率值,即应满足式(6)所示约束。与此同时,发电机发出的有功、无功功率不应超过其出力上、下限,即如式(7)和式(8)所示约束。
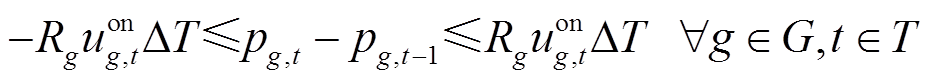 (5)
(5)
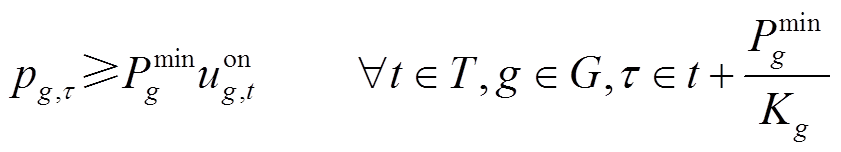 (6)
(6)
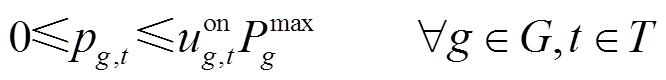 (7)
(7)
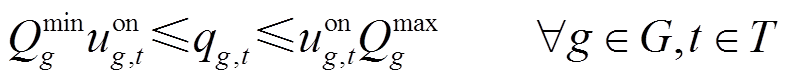 (8)
(8)
式中,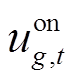 为机组是否并网的二进制变量,
为机组是否并网的二进制变量,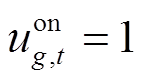 表示机组g时步t并网,否则未并网;Rg为机组有功功率爬坡上限值;ΔT为恢复时步长,由决策者根据实际情况给定;Kg为机组g的频率响应系数;
表示机组g时步t并网,否则未并网;Rg为机组有功功率爬坡上限值;ΔT为恢复时步长,由决策者根据实际情况给定;Kg为机组g的频率响应系数;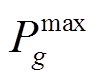 、
、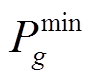 分别为机组g有功出力上、下限;
分别为机组g有功出力上、下限;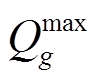 、
、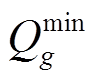 分别为机组g无功出力上、下限。
分别为机组g无功出力上、下限。
2.2.4 负荷节点功率约束
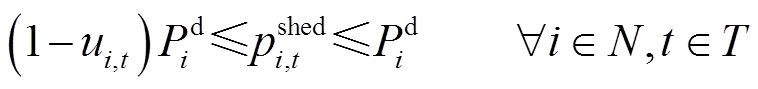 (9)
(9)
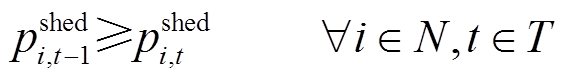 (10)
(10)
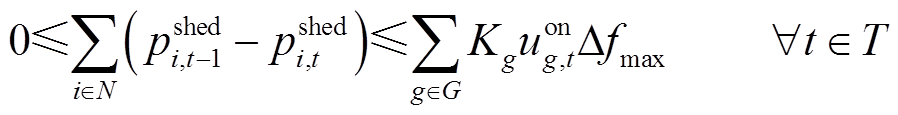 (11)
(11)
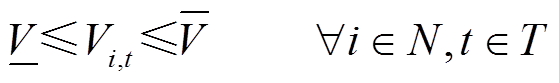 (12)
(12)
式中,Δfmax为系统最大允许频率偏差;Vi,t为母线i在时步t的电压值;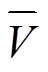 、
、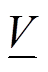 分别为节点电压上、下限。
分别为节点电压上、下限。
式(9)为未恢复负荷有功功率上下限约束;式(10)保证节点i已恢复的负荷不会再次失去供电;式(11)表示负荷恢复操作应在系统频率偏差允许范围内进行;式(12)为系统电压允许波动范围约束。
2.2.5 线路潮流及相位差约束
线路潮流约束采用考虑无功与电压影响的线性化交流潮流约束[22],此处假定支路变比为1,则恢复过程中支路有功无功传输功率约束可以表示为式(13)和式(14)。另外,线路传输有功和无功功率应不超过其功率极限,即式(15)和式(16)所示。
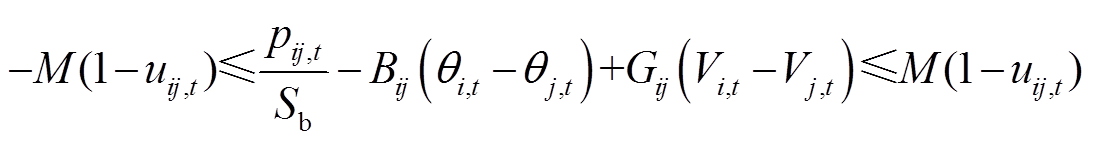
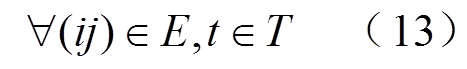
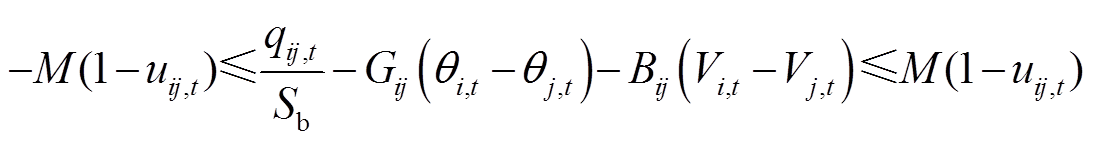
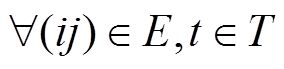 (14)
(14)
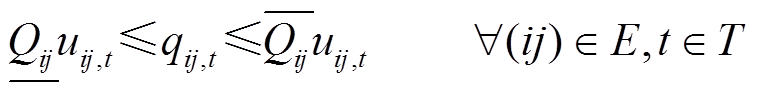 (15)
(15)
 (16)
(16)
 (17)
(17)
式中,Sb为基准功率;Bij、Gij分别为导纳矩阵中节点i与j的互电纳与互电导;θi,t、Vi,t分别为母线i在时步t的相位与电压值;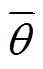 、
、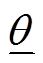 分别为相位差上、下限;
分别为相位差上、下限;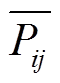 、
、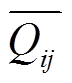 、
、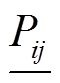 、
、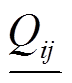 分别为线路ij允许流过的有功、无功功率上、下限;M为足够大正数,根据大M约束原理,当uij,t=1时,输电线路ij已恢复。
分别为线路ij允许流过的有功、无功功率上、下限;M为足够大正数,根据大M约束原理,当uij,t=1时,输电线路ij已恢复。
2.2.6 储能电站运行约束
储能电站具有响应速度快、灵活吞吐电量等特点,在长时间尺度恢复决策时考虑储能电站的调控能够平抑新能源出力不确定性造成的功率波动[23-24]。本文通过储能电站的荷电状态、充放电功率等指标刻画恢复期间储能电站的调控行为,具体为
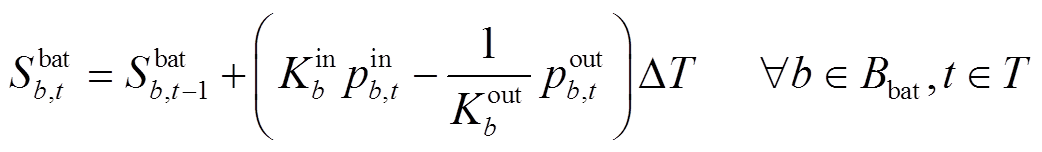 (18)
(18)
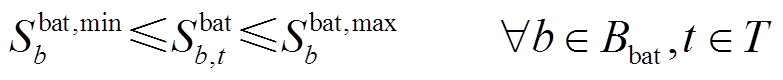 (19)
(19)
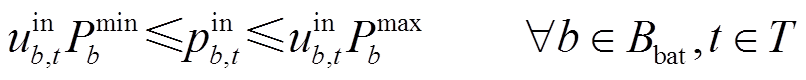 (20)
(20)
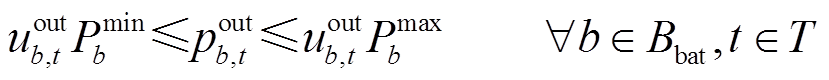 (21)
(21)
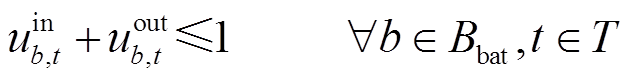 (22)
(22)
式(18)表示t时步储能电站b的充放电功率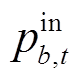 、
、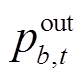 以及t-1时步储能电站b的荷电状态
以及t-1时步储能电站b的荷电状态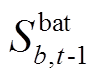 决定了t时步储能电站b的荷电状态
决定了t时步储能电站b的荷电状态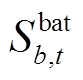 ,
,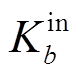 、
、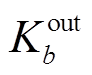 分别为储能电站b的充电、放电效率;式(19)为储能电站荷电状态上下限约束,
分别为储能电站b的充电、放电效率;式(19)为储能电站荷电状态上下限约束,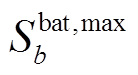 、
、![]() 分别为储能电站b荷电能力上、下限;式(20)和式(21)分别为储能电站充放电功率上、下限约束,
分别为储能电站b荷电能力上、下限;式(20)和式(21)分别为储能电站充放电功率上、下限约束,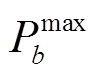 、
、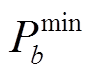 分别为储能电站充放电功率上、下限;式(22)表示储能电站在同一时步只能选择充放电状态中的一种,
分别为储能电站充放电功率上、下限;式(22)表示储能电站在同一时步只能选择充放电状态中的一种,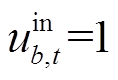 表示储能处于充电状态,
表示储能处于充电状态,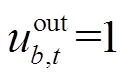 表示储能处于放电状态。
表示储能处于放电状态。
2.2.7 不确定风功率表述
根据鲁棒优化不确定区间的刻画思想,从时间与空间角度将风功率的波动理解为风功率实际波动量到达极限或者说边界的次数[25]。
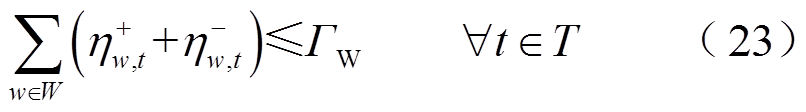
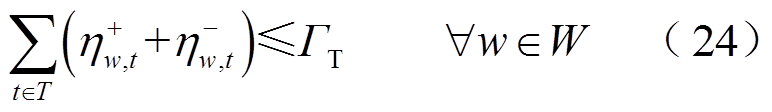
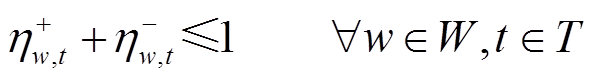 (25)
(25)
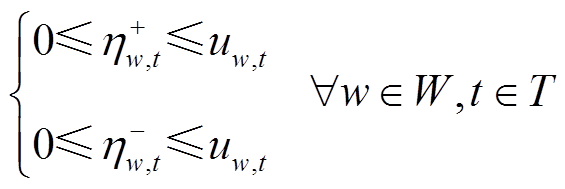 (26)
(26)
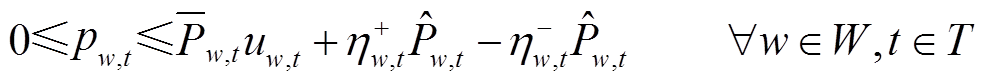 (27)
(27)
式中,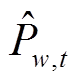 为风电出力预测最大偏差;
为风电出力预测最大偏差;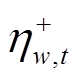 、
、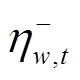 分别为表征风电场w在时步t向上或向下偏离风功率预测值
分别为表征风电场w在时步t向上或向下偏离风功率预测值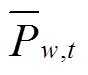 的二元决策变量;
的二元决策变量;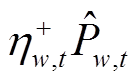 为正向偏差,即超出预测量
为正向偏差,即超出预测量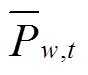 的功率值,
的功率值,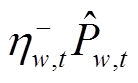 为反向偏差,即少于预测量
为反向偏差,即少于预测量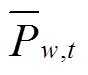 的功率值。需要注意的是
的功率值。需要注意的是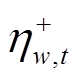 、
、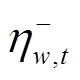 本身为在0与1之间取值的连续量,但根据鲁棒的思想,极限值一定在极值点处取到,因此
本身为在0与1之间取值的连续量,但根据鲁棒的思想,极限值一定在极值点处取到,因此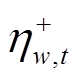 和
和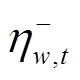 被限定为二进制变量。式(23)中,ΓW表示风电场在空间尺度上波动的不确定预算上限;式(24)中,ΓT表示风电场在时间尺度上波动的不确定预算上限;式(25)表示t时步对于风电场w正负偏差最多发生一次,不可能同时发生;式(26)表示未恢复的风电场不存在偏差量;根据风机桨距角调节与最大功率追踪原理,式(27)限定了在时步t风电场w的风功率pw,t上限,同时暗含了未恢复的风电场节点风功率为0。
被限定为二进制变量。式(23)中,ΓW表示风电场在空间尺度上波动的不确定预算上限;式(24)中,ΓT表示风电场在时间尺度上波动的不确定预算上限;式(25)表示t时步对于风电场w正负偏差最多发生一次,不可能同时发生;式(26)表示未恢复的风电场不存在偏差量;根据风机桨距角调节与最大功率追踪原理,式(27)限定了在时步t风电场w的风功率pw,t上限,同时暗含了未恢复的风电场节点风功率为0。
2.2.8 连通性约束
系统恢复过程中,已恢复网架应保证是连通的,根据流量平衡原理,本文将系统恢复过程中的连通性约束表示为
 (28)
(28)
 (29)
(29)
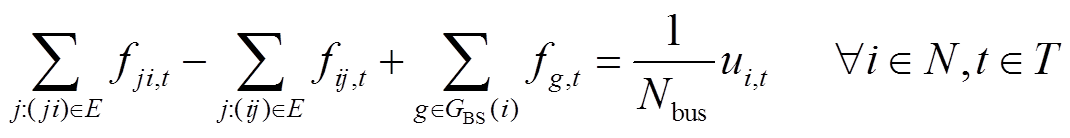 (30)
(30)
式中,GBS为具有黑启动能力的发电机组集合;fg,t为t时步发电机节点g的注入流量;fij,t为t时步线路ij上的流量;Nbus为系统中母线总数。其中,式(28)表示连通区域的数量不超过黑启动机组的数量。
2.2.9 恢复顺序约束
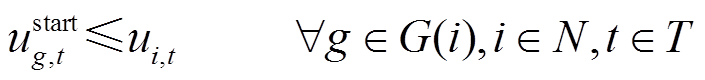 (31)
(31)
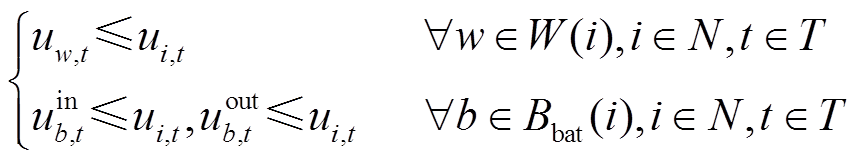 (32)
(32)
 (33)
(33)
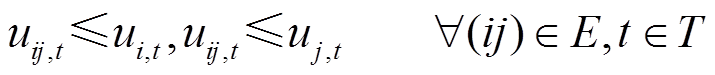 (34)
(34)
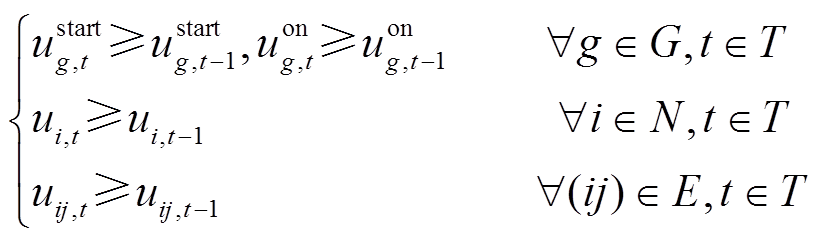 (35)
(35)
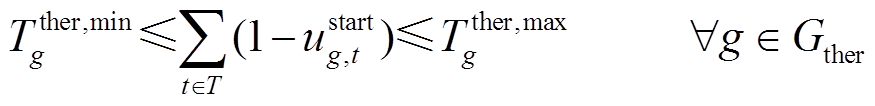 (36)
(36)
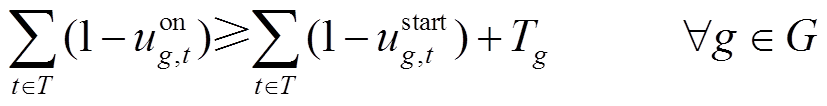 (37)
(37)
式中,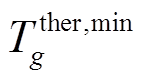 与
与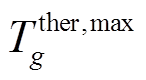 分别为机组的最小、最大启动时间;Gther为所有火电机组集合;Tg为发电机从开机到并网的最小间隔时间。式(31)表示与发电机相连的母线恢复后发电机才能开始启动;式(32)表示与风电场或储能电站相连的母线被恢复后风电场或储能电站才能使用;式(33)表示线路两端母线至少有一端在上一时步被恢复,下一时步这条线路才可以被恢复;式(34)表示如果一条线路ij在时步t被恢复,其两端节点i和j一定在时步t被恢复;式(35)为发电机、母线以及线路恢复顺序约束;式(36)限制了火电机组的最小最大起动时间;式(37)为发电机开机及并网时步关系约束,即发电机g在开机后至少要等Tg才能并网。
分别为机组的最小、最大启动时间;Gther为所有火电机组集合;Tg为发电机从开机到并网的最小间隔时间。式(31)表示与发电机相连的母线恢复后发电机才能开始启动;式(32)表示与风电场或储能电站相连的母线被恢复后风电场或储能电站才能使用;式(33)表示线路两端母线至少有一端在上一时步被恢复,下一时步这条线路才可以被恢复;式(34)表示如果一条线路ij在时步t被恢复,其两端节点i和j一定在时步t被恢复;式(35)为发电机、母线以及线路恢复顺序约束;式(36)限制了火电机组的最小最大起动时间;式(37)为发电机开机及并网时步关系约束,即发电机g在开机后至少要等Tg才能并网。
根据两阶段鲁棒优化的思想,上述系统恢复模型可以表示为两个阶段的优化问题:第一阶段先确定决策变量u,即系统恢复中发电机、母线、线路等元件的恢复次序;第二阶段包含两层,第一层最大化不确定量对系统造成的影响,第二层调整系统运行状态来应对不确定性带来的影响。在第一阶段决策变量u已知的前提下,第二阶段求解模型
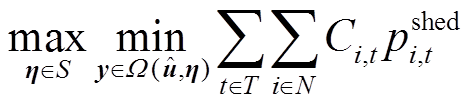 (38)
(38)
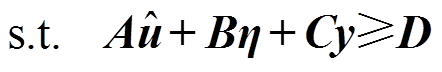 (39)
(39)
式中,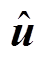 为第一阶段已确定的决策向量;
为第一阶段已确定的决策向量;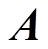 为其系数矩阵;
为其系数矩阵;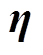 和
和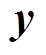 分别为第二阶段第一、二层决策向量;B、C分别为其系数矩阵;D为约束右端项。不难看出,第二阶段优化模型是一个两层优化模型,无法直接求解,需要进行对偶转化,即将双层最大最小化问题转化为双层最大化问题,即
分别为第二阶段第一、二层决策向量;B、C分别为其系数矩阵;D为约束右端项。不难看出,第二阶段优化模型是一个两层优化模型,无法直接求解,需要进行对偶转化,即将双层最大最小化问题转化为双层最大化问题,即
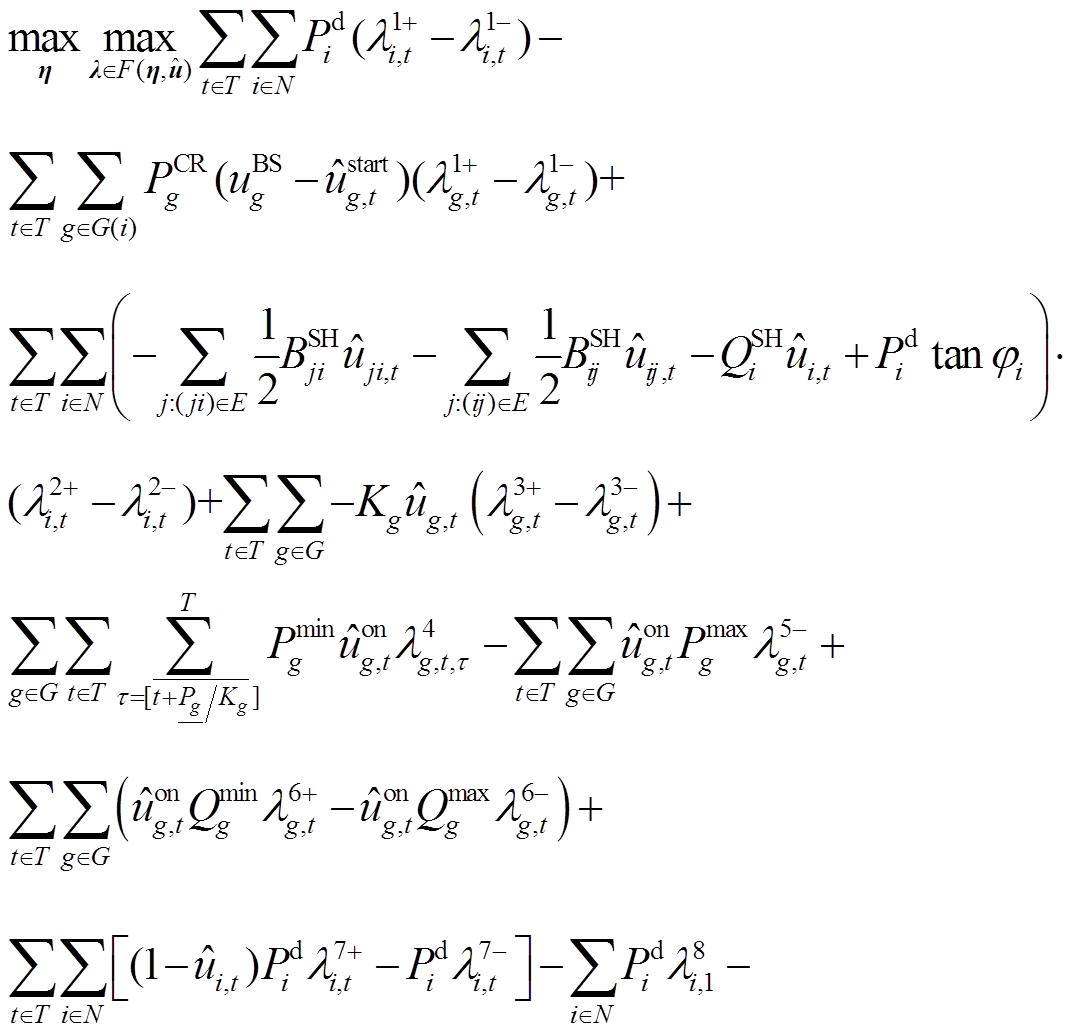
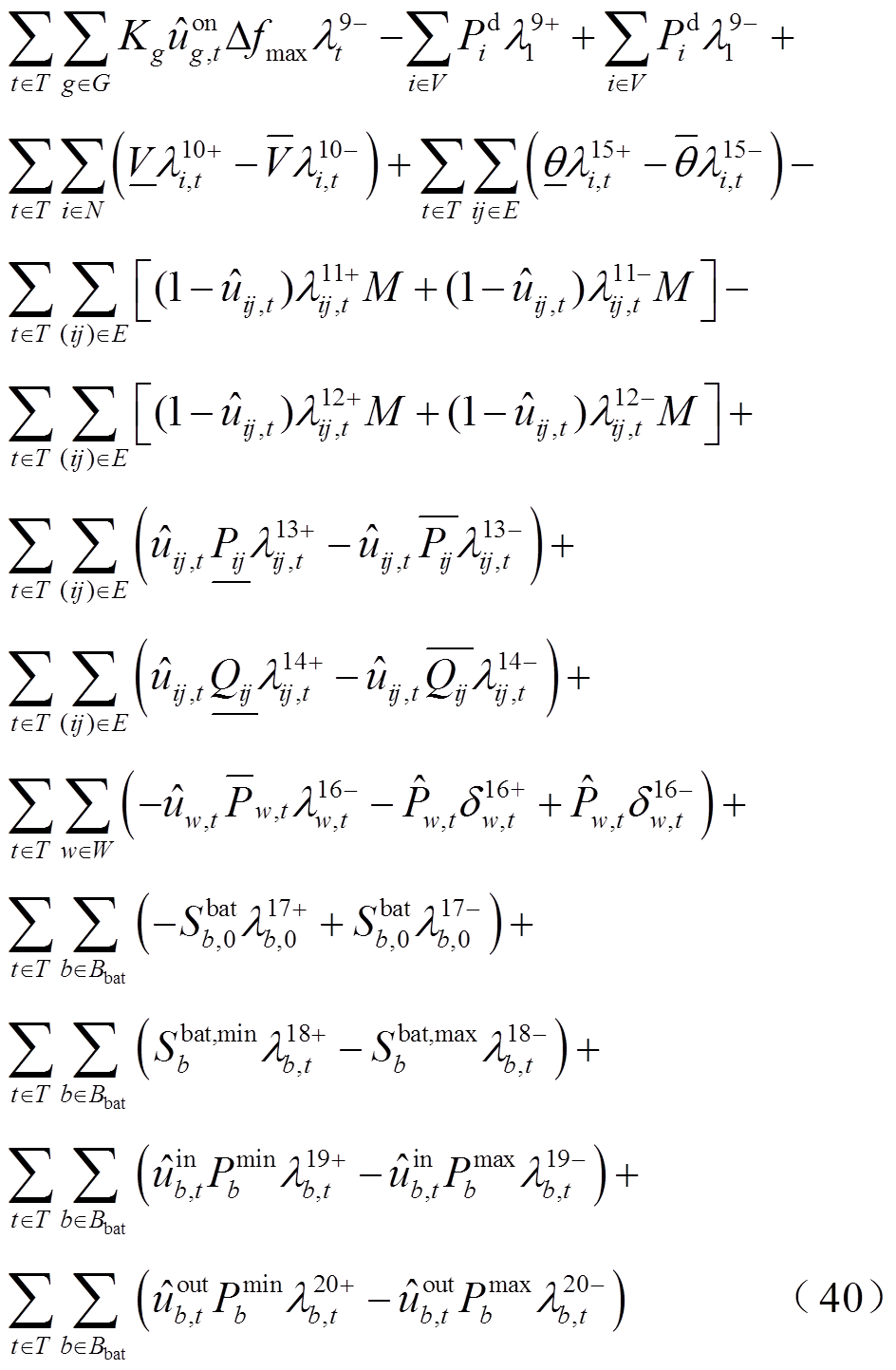
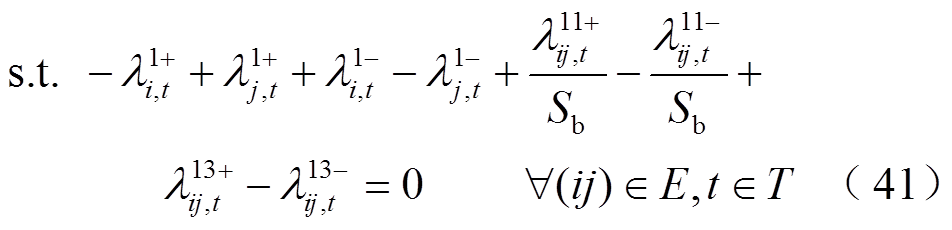
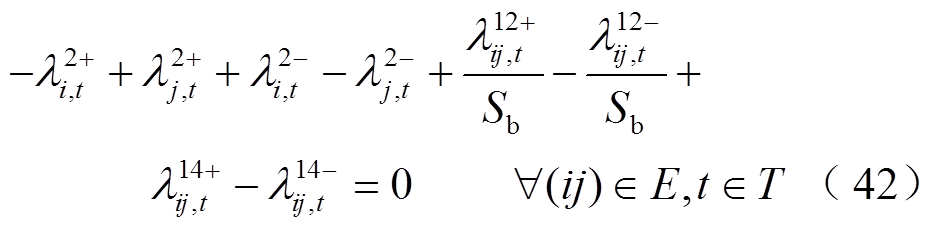
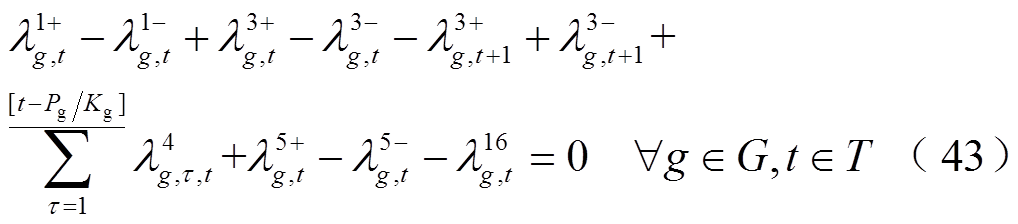
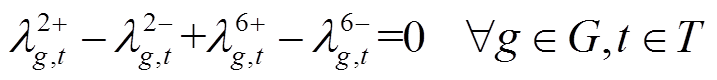 (44)
(44)
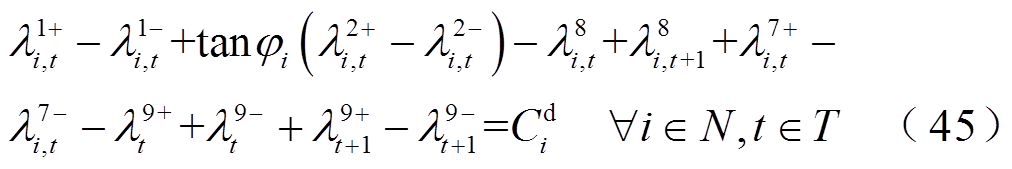
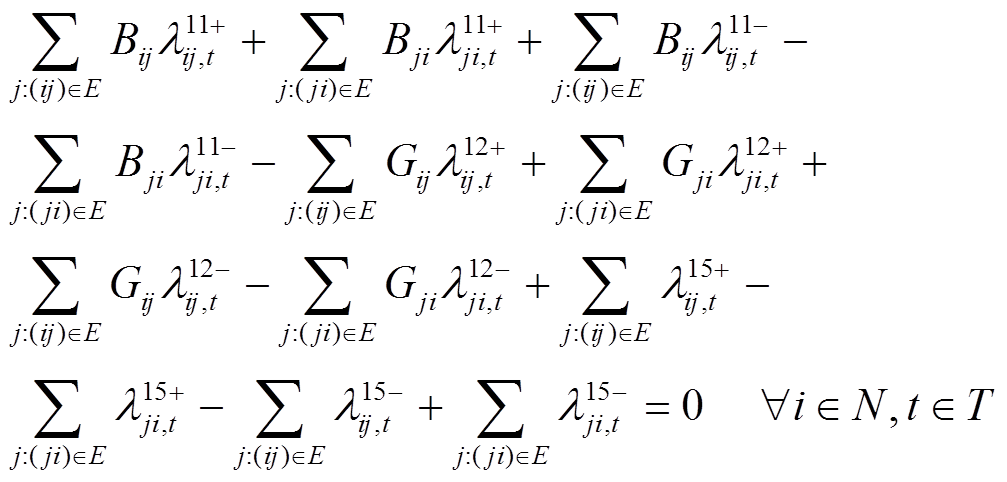 (46)
(46)
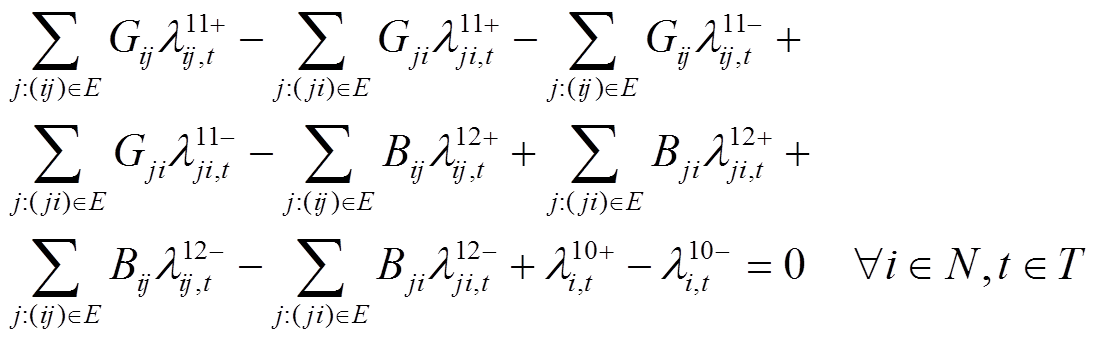 (47)
(47)
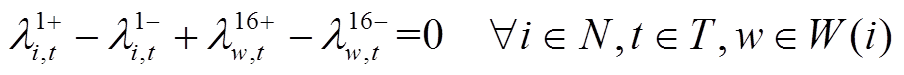 (48)
(48)
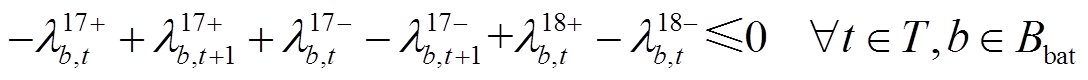 (49)
(49)
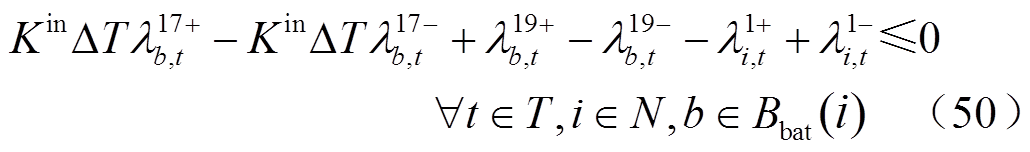
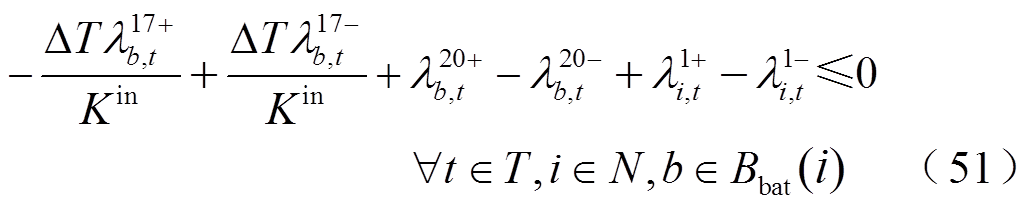
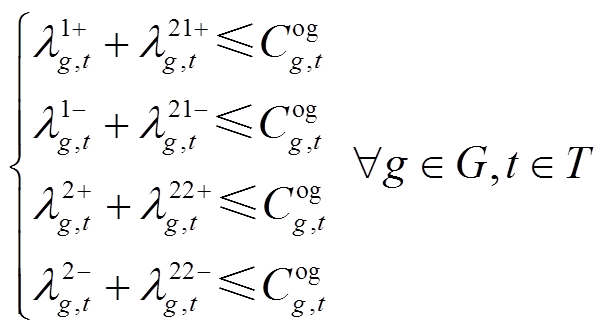 (52)
(52)
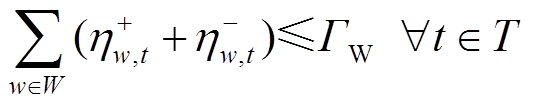 (53)
(53)
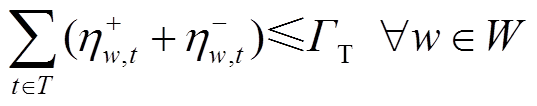 (54)
(54)
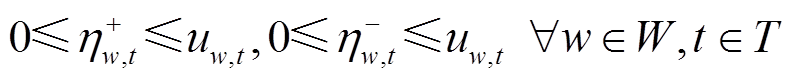 (55)
(55)
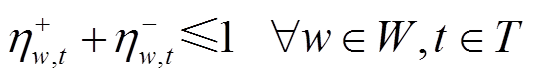 (56)
(56)
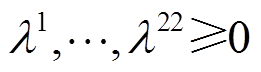 (57)
(57)
式中,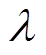 为本文全过程恢复优化模型的对偶变量,其中
为本文全过程恢复优化模型的对偶变量,其中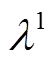 ~
~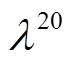 依次为式(3)~式(17)、式(27)、式(18)~式(21)的对偶变量,例如
依次为式(3)~式(17)、式(27)、式(18)~式(21)的对偶变量,例如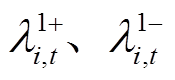 为式(3)所对应对偶变量,
为式(3)所对应对偶变量,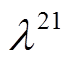 、
、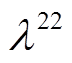 为保证式(2)中松弛变量非负引入的对偶变量。需要注意的是,在式(40)中,
为保证式(2)中松弛变量非负引入的对偶变量。需要注意的是,在式(40)中,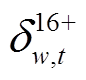 为
为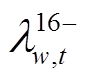 和
和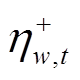 的交叉乘积项,
的交叉乘积项,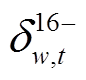 为
为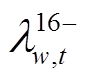 和
和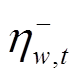 的交叉乘积项,需要线性化,以
的交叉乘积项,需要线性化,以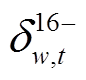 为例,线性化公式为
为例,线性化公式为
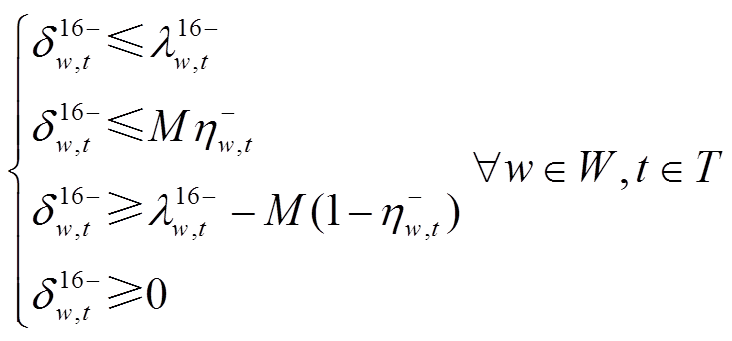 (58)
(58)
外层第一阶段模型根据内层第二阶段模型通过对偶转化求解得到极端风电波动场景集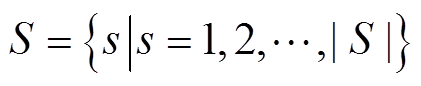 ,继续优化系统恢复方案,其模型可以表示为
,继续优化系统恢复方案,其模型可以表示为
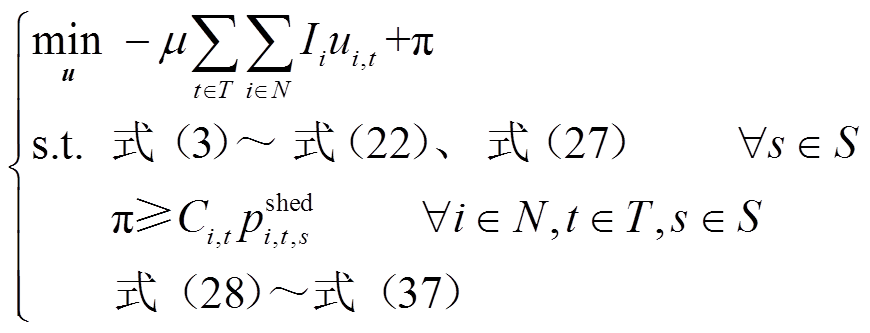 (59)
(59)
根据C&CG算法实现架构,转化后的两层模型通过主子问题分解迭代求解,主子问题的表述形式见3.1节,具体的迭代步骤如下:
(1)以风电场预测功率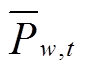 作为风功率Pw,t输出功率上限,即不考虑风功率波动场景,得到系统元件最优恢复顺序方案,假定为u1,其对应目标函数值记为UB1。根据u1解出其对应的最恶劣风电波动场景,记为s1,将其并入风电波动场景集S0中,其对应目标函数假定为LB1。将UB1和LB1作为初始上下界,即UB=UB1,LB=LB1,同时设置迭代次数k=1,迭代阈值к。
作为风功率Pw,t输出功率上限,即不考虑风功率波动场景,得到系统元件最优恢复顺序方案,假定为u1,其对应目标函数值记为UB1。根据u1解出其对应的最恶劣风电波动场景,记为s1,将其并入风电波动场景集S0中,其对应目标函数假定为LB1。将UB1和LB1作为初始上下界,即UB=UB1,LB=LB1,同时设置迭代次数k=1,迭代阈值к。
(2)令k=k+1,求解式(59)所示的主问题,得到新的系统恢复方案uk,同时比较主问题的目标函数值Rmas与LB的大小,如果Rmas≥LB,则LB=Rmas。
(3)根据步骤(2)中的系统恢复方案uk,求解式(40)~式(57)所示的子问题,得到步骤2系统恢复方案下对系统影响最恶劣的风功率波动场景sk,进而得到当前风功率波动场景集 ,同时比较子问题目标函数Rsub与UB的大小,如果Rsub≤UB,则UB=Rsub。
,同时比较子问题目标函数Rsub与UB的大小,如果Rsub≤UB,则UB=Rsub。
(4)判断|(UB-LB)/LB|的大小,如果小于迭代阈值к,则停止迭代;否则转回步骤(2),继续迭代过程。
上述两阶段鲁棒优化主问题为混合整数线性规划(Mixed Integer Linear Programming, MILP)模型,混合整数变量会降低模型求解速度,实际中可以通过一些启发式方法确定优化模型的初始解,在此基础上搜索一定间隙下的最优解。本文根据系统恢复过程的特性,提出一种启发式搜索初始解的方法,分为两个阶段:第一阶段根据系统恢复特性,确定要恢复的目标网架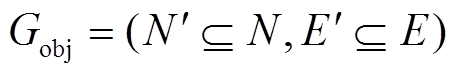 ;第二阶段将主问题MILP模型中要恢复的目标网架限定为Gobj并求解主问题模型,将求解所得结果作为主问题的初始解。其中第一阶段确定目标网架时借鉴网架重构阶段骨架网络生成思想[12],分为两步:第一步确定源汇点集;第二步根据流量平衡原理确定由这些源汇点集按照一定的目标生成的最小斯坦森树,即为初始解对应的目标网架Gobj。其中在第一步确定源汇点集时将所有发电机节点包含在源汇点集合中,其余非发电机节点按照一定的比例选入到源汇点集合中,按照非发电机节点重要性评估准则由大到小选入。
;第二阶段将主问题MILP模型中要恢复的目标网架限定为Gobj并求解主问题模型,将求解所得结果作为主问题的初始解。其中第一阶段确定目标网架时借鉴网架重构阶段骨架网络生成思想[12],分为两步:第一步确定源汇点集;第二步根据流量平衡原理确定由这些源汇点集按照一定的目标生成的最小斯坦森树,即为初始解对应的目标网架Gobj。其中在第一步确定源汇点集时将所有发电机节点包含在源汇点集合中,其余非发电机节点按照一定的比例选入到源汇点集合中,按照非发电机节点重要性评估准则由大到小选入。
本文将网络拓扑分析的节点重要度和归一化后的非发电机节点总负荷量两个指标按照一定比例作为非发电机节点的节点重要性权重系数。需要注意的是,本文在启发式获取多组初始解后,可以根据这些初始解并行求解主问题,最终主问题的求解时间取决于效果最佳的启发式初始解。
上述考虑风电预测误差的两阶段鲁棒恢复模型求解过程如图2所示。
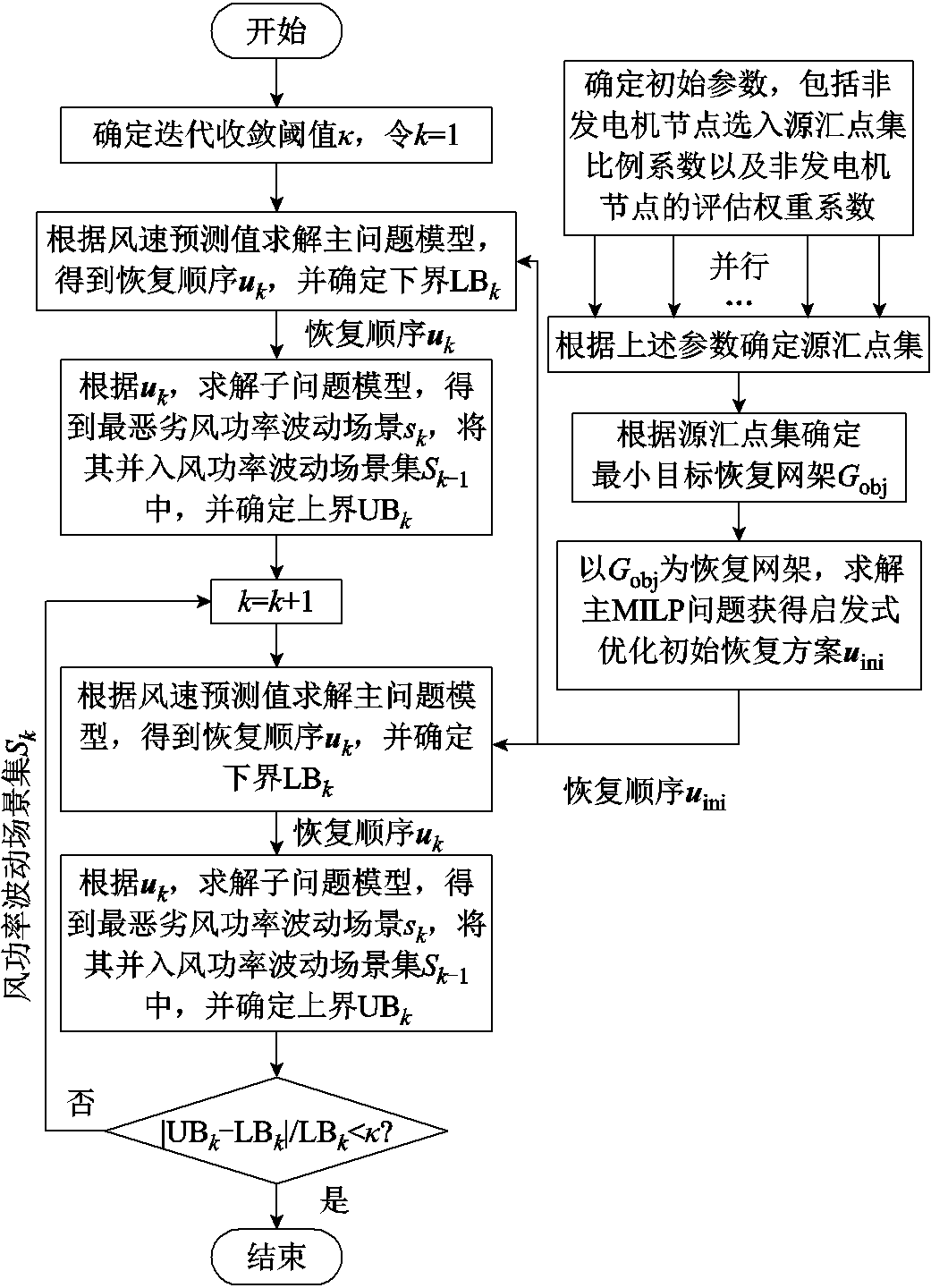
图2 两阶段鲁棒优化模型求解流程
Fig.2 Two stage robust optimization model solving process
为了说明所提方法的可行性与有效性,本文通过新英格兰10机39节点系统与某实际电网算例对上述模型进行验证。主子问题的建模与求解在Matlab软件的Yalmip平台上完成,求解时调用GUROBI求解器进行。计算采用普通个人计算机,配置为Intel(R) Core(TM) i5—8300H CPU @2.30GHz,安装内存为8GB。
首先采用新英格兰10机39节点系统进行测试,系统共包含39个节点、46条线路、10台发电机组,系统拓扑图如附图1所示。根据式(33)、式(34)的母线、线路恢复逻辑,每个恢复时步用时考虑为一条母线及一条线路恢复用时的叠加,参考相关文献中母线、线路恢复用时取值[26-27],设定恢复步长为10min。另外,根据待恢复系统规模大小,确定全过程恢复总时步数为20。发电机G1设为黑启动机组,其余发电机均设定为非黑启动机组,详细参数见附表1。设置线路1-39、2-30、6-31、10-32、19-33、20-34、22-35、23-36、25-37、29-38的有功功率和无功功率限制分别为200MW和200Mvar;其余线路的有功功率和无功功率限制分别为100MW和100Mvar。节点3、5、14、16和17处有5座风电场,风电场的恢复全过程预测出力曲线如附图2所示,风功率预测误差取为预测出力的0.3倍,同时假定风电机组功率因数为1。节点3、15处有两座电化学储能电站,储能电站规模为5MW/10MW·h,充放电效率取为0.95,存储能量运行范围取为10%~90%,初始存储能量取为50%。负荷节点权重系数在0.8~1范围内取值。C&CG迭代收敛阈值设定为0.01。
4.1.1 结果展示与分析
本文建立的全过程两阶段鲁棒优化模型所得结果主要为适应于风电波动场景的元件恢复次序。为更直观地展示元件恢复次序决策结果,在给定元件恢复次序的前提下,本文也基于风电出力场景得到了具体的长时间尺度厂站恢复预案。
1)元件恢复次序决策
由于风功率波动及目标函数中节点重要度因素系数的设置均会影响元件恢复次序的决策。为分析风电波动对元件恢复次序的影响,首先将μ值设为0,也即仅考虑风电波动对元件恢复次序的影响,风功率波动参数ΓT、ΓW取为10和5,在不考虑风电预测误差(方案1)及考虑风电预测误差(方案2)两种方式下得到元件恢复次序优化结果,见表1。
从表1可以看出,考虑风电预测误差后由于需兼顾极端风功率波动场景造成的起动功率缺额,因此与不考虑风电预测误差的恢复计划相比,机组G2、G4、G6并未在0~20时步恢复时段范围内启动。不考虑风电预测误差情况下,第10时步,通过线路4-5、线路5-6首次合环,消除线路4-14过载;考虑风电预测误差后,同样在第10时步,通过线路14-15首次合环,消除极端风电波动场景造成的线路3-4以及线路3-18潮流越限。在第20时步考虑及不考虑风电预测误差的恢复计划均形成了包含若干环网的已恢复网架,如图3所示(实线表示已恢复线路,虚线表示未恢复线路)。
表1 IEEE-39节点系统机组、线路恢复顺序
Tab.1 Units and lines restoration sequence of IEEE-39 bus system
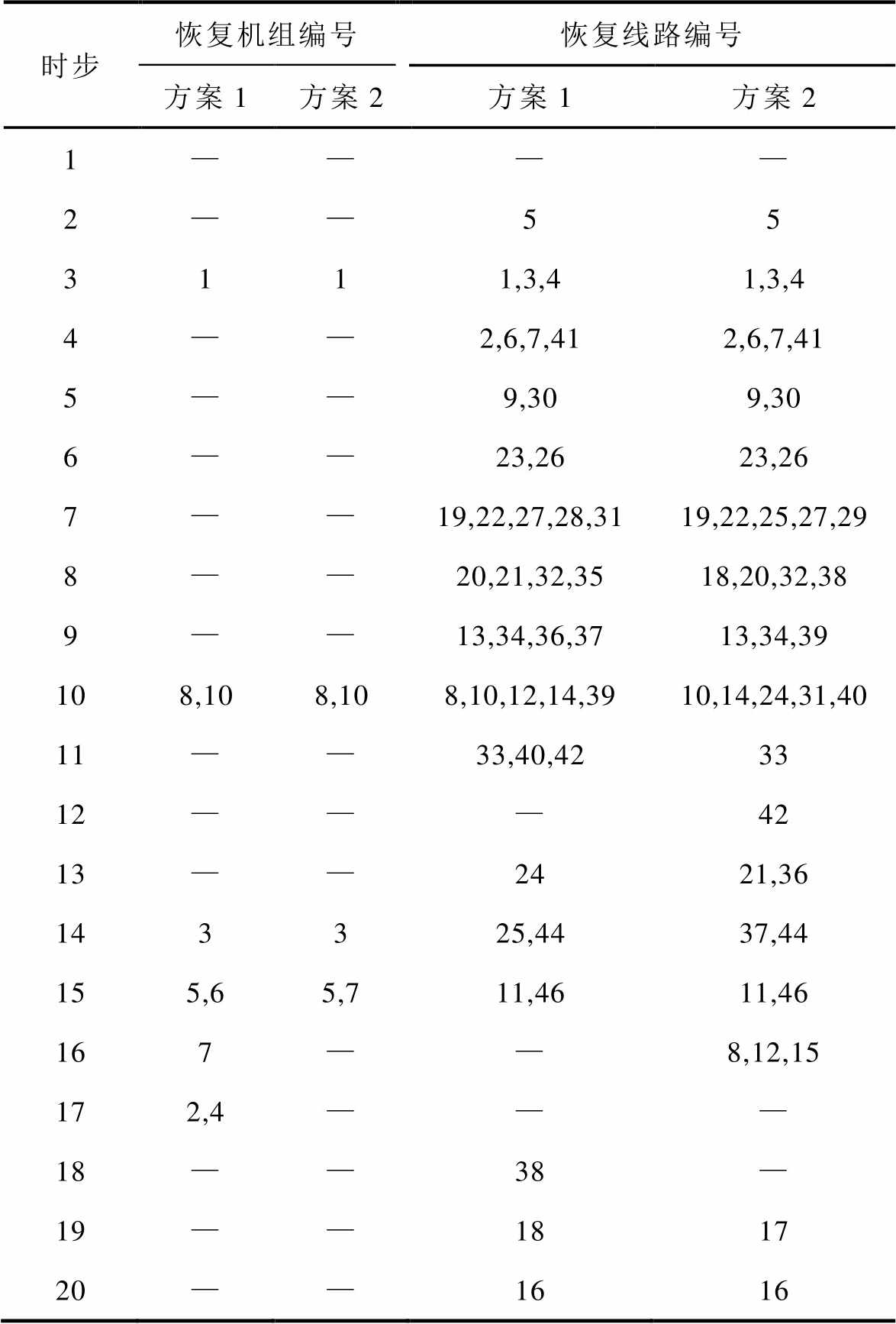
时步恢复机组编号恢复线路编号 方案1方案2方案1方案2 1———— 2——55 3111,3,41,3,4 4——2,6,7,412,6,7,41 5——9,309,30 6——23,2623,26 7——19,22,27,28,3119,22,25,27,29 8——20,21,32,3518,20,32,38 9——13,34,36,3713,34,39 108,108,108,10,12,14,3910,14,24,31,40 11——33,40,4233 12———42 13——2421,36 143325,4437,44 155,65,711,4611,46 167——8,12,15 172,4——— 18——38— 19——1817 20——1616
由图3可见,与不考虑风电预测误差相比,考虑风电预测误差后线路7-8以及线路9-39也会闭合成环以减轻极端风电波动场景造成的潮流越限。
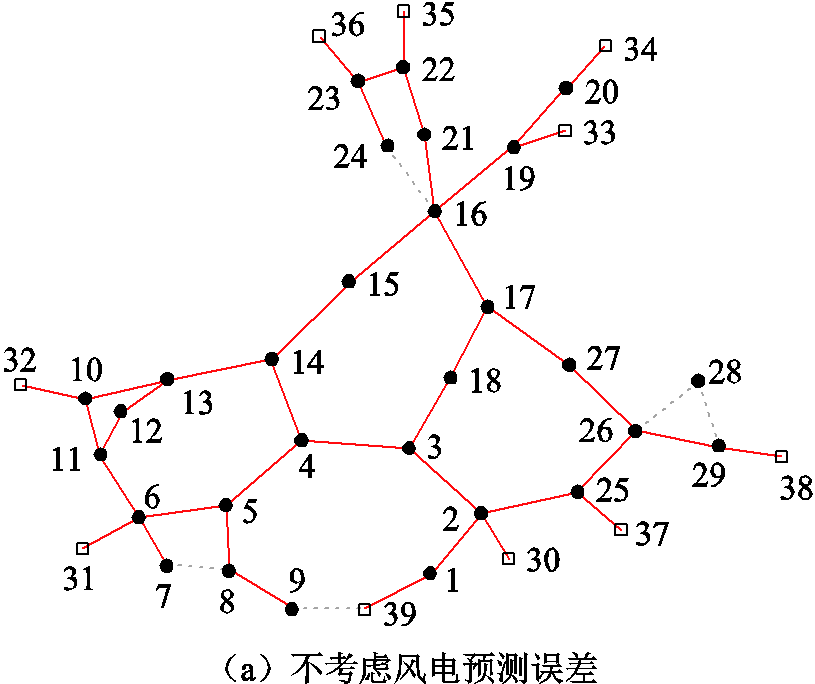
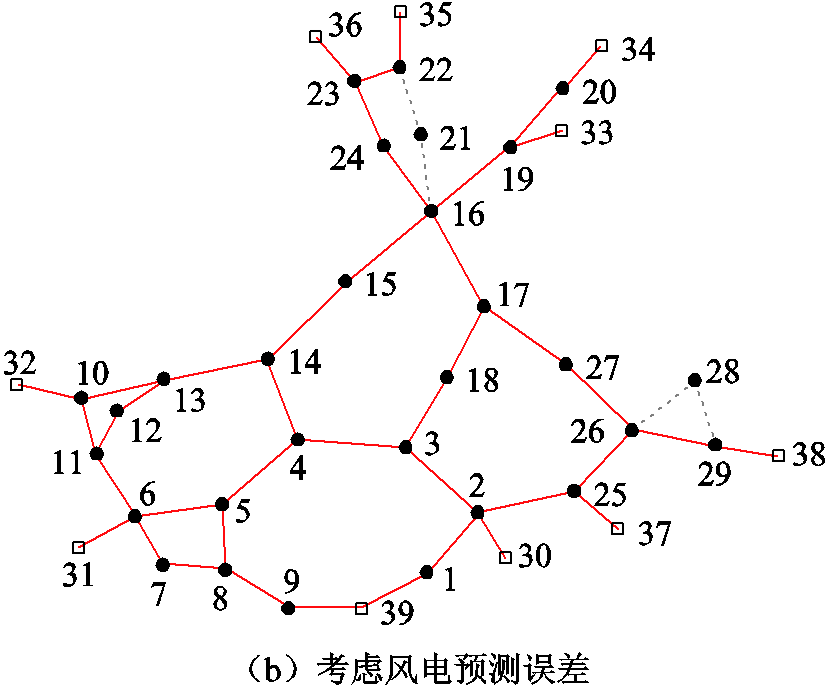
图3 第20时步已恢复网架示意图
Fig.3 Schematic diagram of restored network at time step 20
另外,为分析节点重要度因素对元件恢复次序的影响,将μ值设为100。节点重要度依据文献[12]所提方法进行评估。应用C&CG算法迭代三次后得到优化方案,耗时254s。选取第9时步的恢复路径优化结果,与不考虑节点重要度因素的恢复路径优化结果对比,如图4所示(实线表示已恢复线路,虚线表示未恢复线路)。可以看到,考虑节点重要度因素会对机组所在母线恢复顺序产生一定影响,进而影响机组恢复顺序。具体来讲,不考虑节点重要度时,在第9时步时,机组G2所在母线31并未恢复,而机组G7所在母线36已经恢复;而考虑节点重要度因素后,G2、G7所在母线恢复情况正好相反。结合节点重要度评估指标可以看出,考虑节点重要度因素后,第9时步时,系统恢复路径上的节点重要度权值之和变大,恢复路径略有调整。
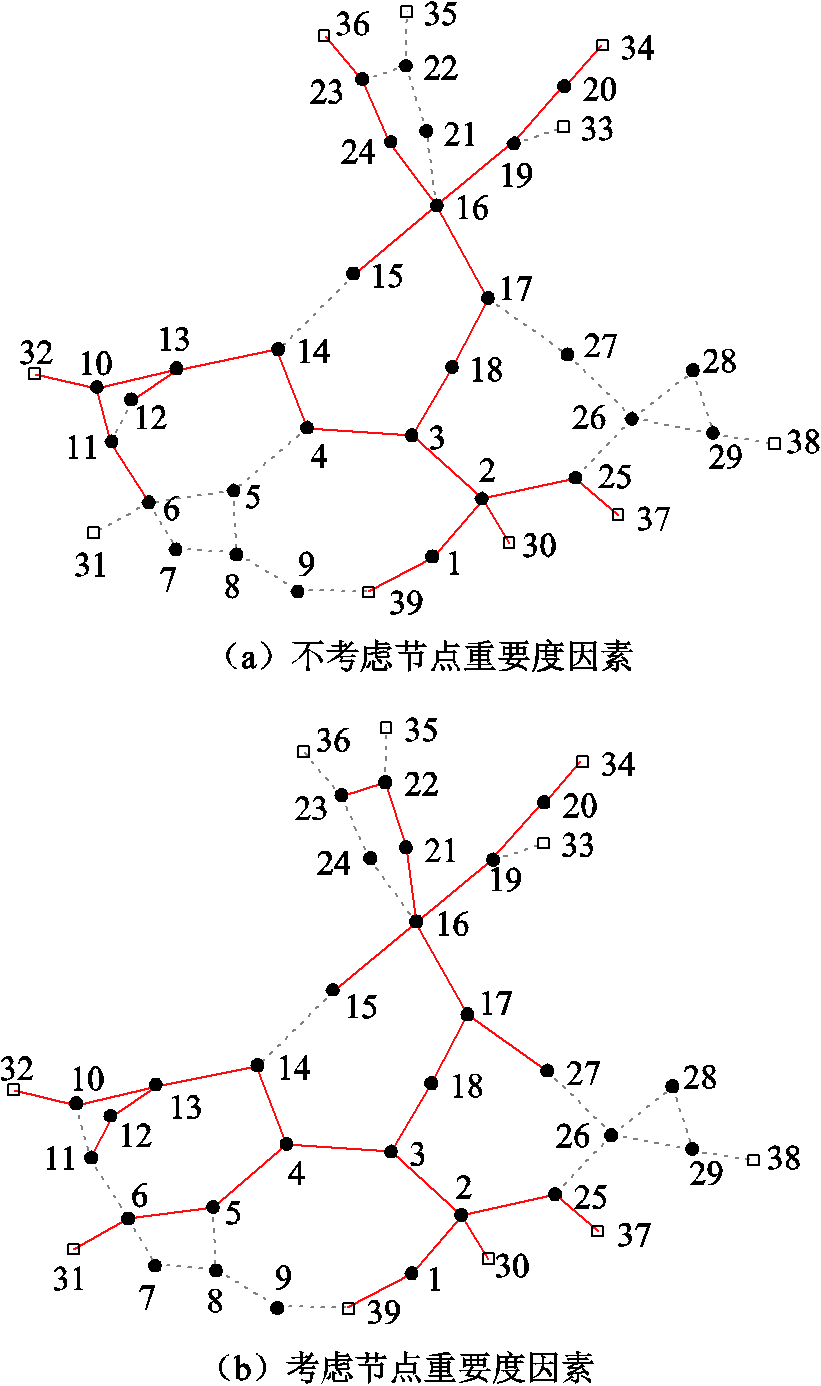
图4 第9时步已恢复网架示意图
Fig.4 Schematic diagram of restored network at time step 9
2)厂站恢复方案
在元件恢复顺序给定的情况下,厂站恢复计划基于若干典型风电出力场景求解全过程恢复模型得到(具体公式见附录式(A1))。由于元件恢复次序已通过本文两阶段鲁棒优化模型求得,因此,此问题变成易于求解的线性规划问题。图5分别展示了0~20恢复时步已恢复节点重要度总和、负荷恢复总量、风电总调度出力及储能电站荷电状态(元件恢复次序使用μ=100优化结果)。
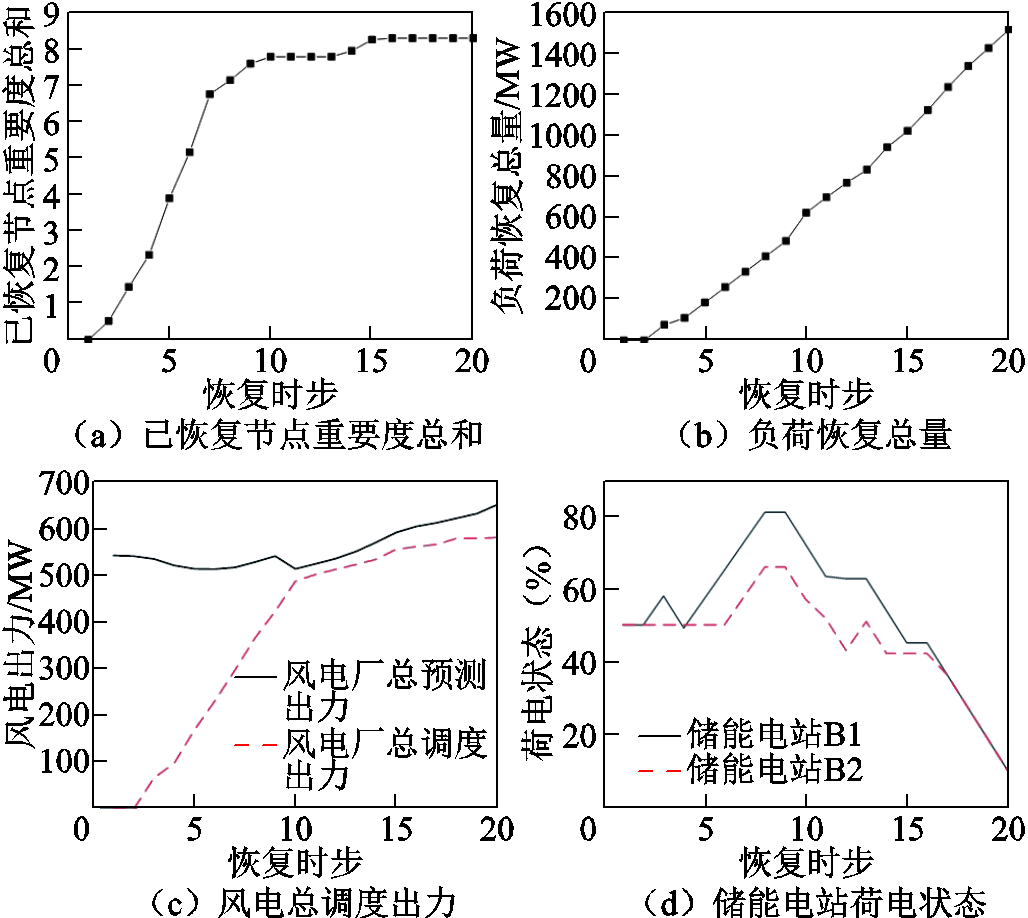
图5 厂站恢复方案优化结果
Fig.5 Optimization results of plants and stations restoration scheme
从图5a可以看出,第16时步已恢复节点重要度总和达到最大值8.25;图5b中,第20时步负荷恢复总量达到1 514.211MW;图5c为第0~20时步风电场总调度出力,在第3~6时步,5座风电场所连母线陆续恢复;图5d为第0~20时步两座储能电站的荷电状态。可以看到,两座储能电站在大部分恢复时段处于放电状态,最终在第20时步,两座储能电站均到达最低荷电状态。
4.1.2 不确定预算对方案结果的影响
上述考虑风功率预测误差的鲁棒恢复模型包含时空不确定预算参数。图6展示了调节不确定参数ΓW和ΓT对结果的影响。
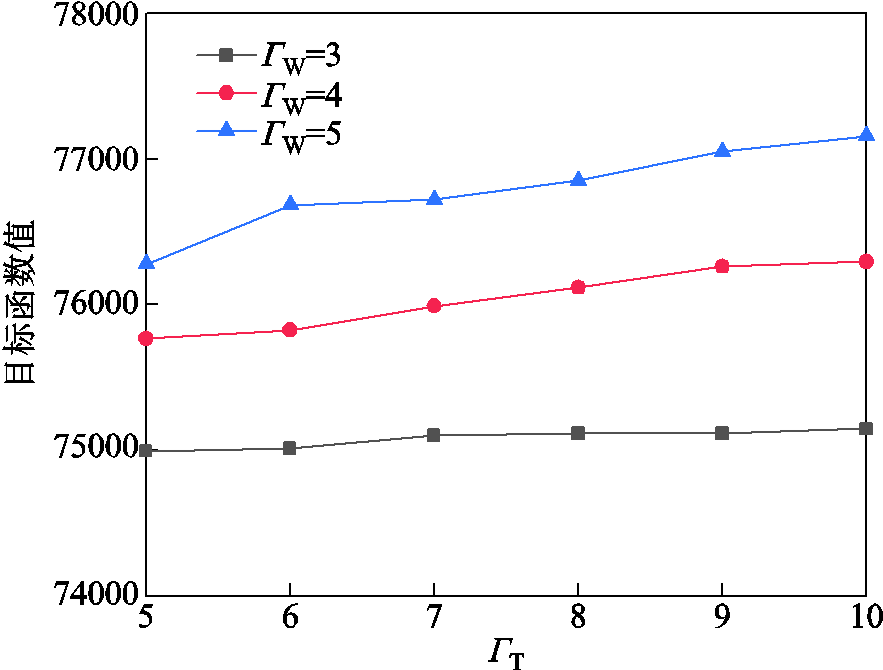
图6 不确定参数ΓW和ΓT对目标函数值的影响
Fig.6 Influence of uncertain parameters ΓW and ΓT on objective function value
从图6可以看出,对于相同的ΓW而言,增大ΓT会导致目标函数值增加,即考虑已恢复节点重要度与负荷恢复效益的目标函数值变差(目标函数为最小化问题);对于相同的ΓT而言,增大ΓW值同样会导致目标函数值增加,所得恢复方案更保守。另外,当不确定预算参数ΓT达到一定值后,通过调节ΓT目标函数值不再变化,即实际恢复中为规避不确定量给系统恢复带来的风险,鲁棒参数调节存在一定的饱和度,当鲁棒参数达到某饱和值后,已不能通过调节鲁棒参数降低恢复风险。
4.1.3 优化结果对风电不确定出力的适应性分析
优化结果对风电不确定出力的适应性包括元件恢复次序与基于给定元件恢复次序的厂站恢复方案适应性两方面。
由两阶段鲁棒优化架构可知,第一阶段所得元件恢复顺序适应于第二阶段生成的极端风电波动场景集。因此,可以认为只要风电不确定出力变化未超出设定的鲁棒预算范围,第一阶段优化结果将完全适应风电不确定出力变化。为说明两阶段鲁棒优化架构所得元件恢复次序对极端风电波动场景的适应性,在理论上的最极端风电波动场景下(各时步风电出力均取预测出力下界),使用4.1.1节μ=0元件次序优化结果,能够在不调整元件恢复次序的前提下得到可行的厂站恢复方案。图7为在理论上的最极端风电波动场景下,使用本文鲁棒优化方法进行长时间尺度恢复模拟所得各时步负荷恢复总量。
在元件恢复次序给定的情况下,厂站恢复方案对风电不确定出力的适应性可从不同风功率波动场景下的功率调节量上体现,功率调节量越小说明厂站恢复方案的适应性越强。由于厂站恢复方案根据给定的元件恢复次序并基于典型场景得到,典型场景的数量与代表性决定了厂站恢复方案的适应性。为了说明典型场景数量对厂站恢复方案适应性的影响,选择不同数量的典型场景得到厂站恢复方案,在风电出力预测区间内随机抽取50组场景,计算这些场景下厂站恢复方案的功率调节量。图8以箱线图形式展示了在50组风电出力场景下,基于不同数量典型场景制定厂站恢复方案的功率调节量。从图8中可以看出,随着典型场景数量的增加,厂站恢复方案对于不同风电波动场景的功率调节量大小及变化区间均在减小。
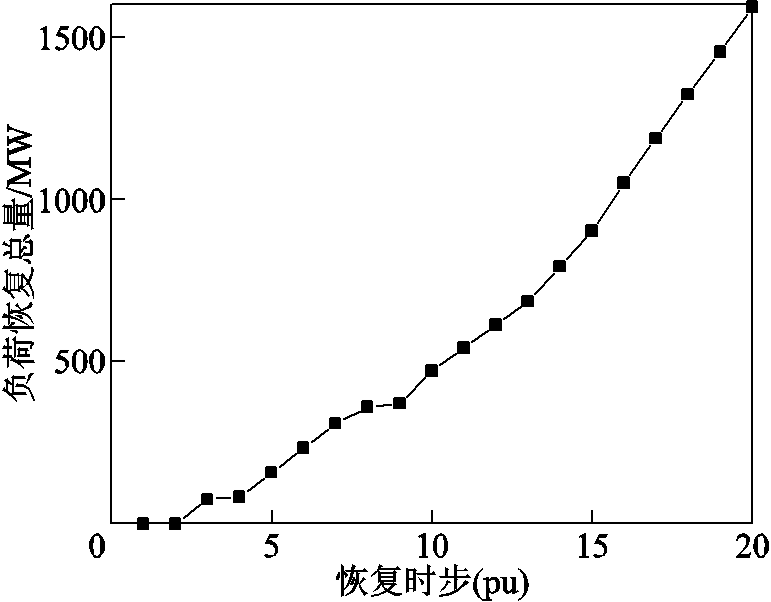
图7 各时步负荷恢复总量
Fig.7 Total load restoration amount in each period
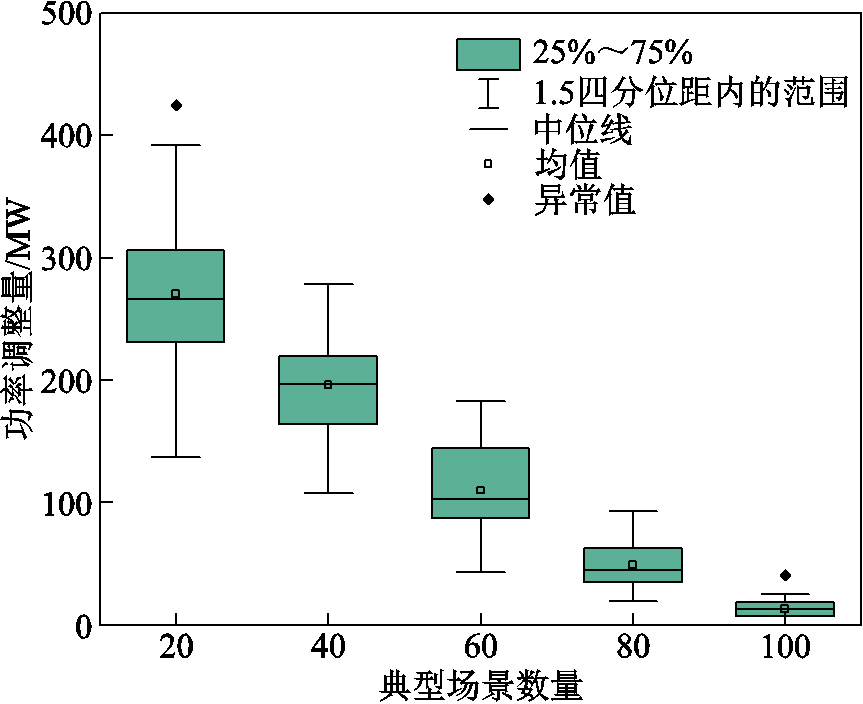
图8 功率调节量箱线图
Fig.8 Power adjustment amount box diagram
4.1.4 方案对比
首先选择两种典型的恢复决策建模方式对比说明本文全过程恢复建模方式在长时间尺度恢复决策方面的优势,然后基于全过程恢复模型说明本文两阶段鲁棒优化方法较随机优化在元件恢复次序决策方面的优势。
1)两种典型的恢复决策建模方式与全过程恢复建模方式对比
第一种典型的恢复决策方式综合考虑线路充电无功功率、发电及负荷恢复量等因素以贪婪搜索方式搜索恢复路径[4];第二种典型的恢复决策方式以充电无功总量最小为目标,搜索包含目标节点的局部最小生成树[28],以局部最小生成树为送电路径恢复各目标节点,然后外扩恢复局部最小生成树外的非目标节点。为方便对比分析,暂不考虑风电出力的不确定性,同时在恢复时步建模时统一了三种恢复决策方式的时间刻度。图9为应用三种恢复决策方式在0~20时步的负荷恢复总量。
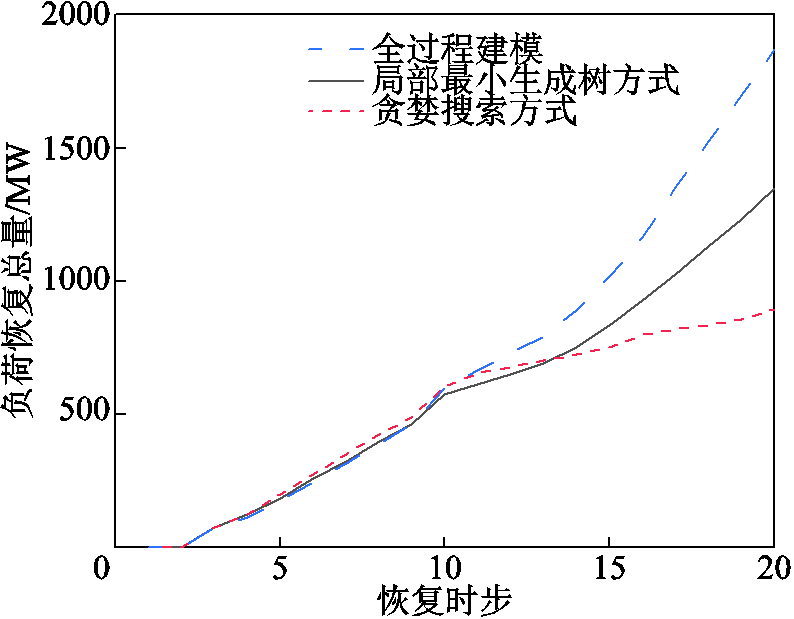
图9 三种恢复决策方式的负荷恢复总量
Fig.9 Total load restoration amount of three restoration decision-making methods
从图9可见,全过程建模方式的负荷恢复总量最大,主要因为全过程建模方式对20个恢复时步进行总体决策并全局寻优,考虑了长时间尺度恢复决策的后效性,因此总体效果要好于其他两种传统恢复决策方式。局部最小生成树方式则由于是基于图论算法盲目进行决策,其恢复效果也劣于全过程建模方式。
2)基于多典型场景的随机优化方法与本文鲁棒优化方法对比
应用全过程建模处理考虑风电不确定性的长时间尺度恢复决策问题可应用随机与鲁棒两种优化方法。文献[14]通过随机优化方法研究了考虑风电接入的长时间尺度恢复决策问题,但基于典型场景建模的随机优化方法所得元件恢复次序决策虽然在典型风电出力场景下具有较高质量,然而在极端风电出力场景下鲁棒性可能更差,甚至可能失效。为了说明本文鲁棒优化方法的优势,使用多组风电出力场景,聚类后得到10组典型风电出力场景,即集合K中包含10组典型场景。根据随机优化模型(附录式(A2))进行优化,得到元件恢复次序usto。另外假定4.1.1节中μ=0时元件恢复次序为uro。将上述元件恢复次序决策应用到典型以及极端(设定鲁棒阈值下)风电出力场景下的长时间尺度恢复模拟。随机与鲁棒优化方法所得典型以及极端(设定鲁棒阈值下)风电出力场景下20个恢复时步的负荷恢复总量如图10所示。
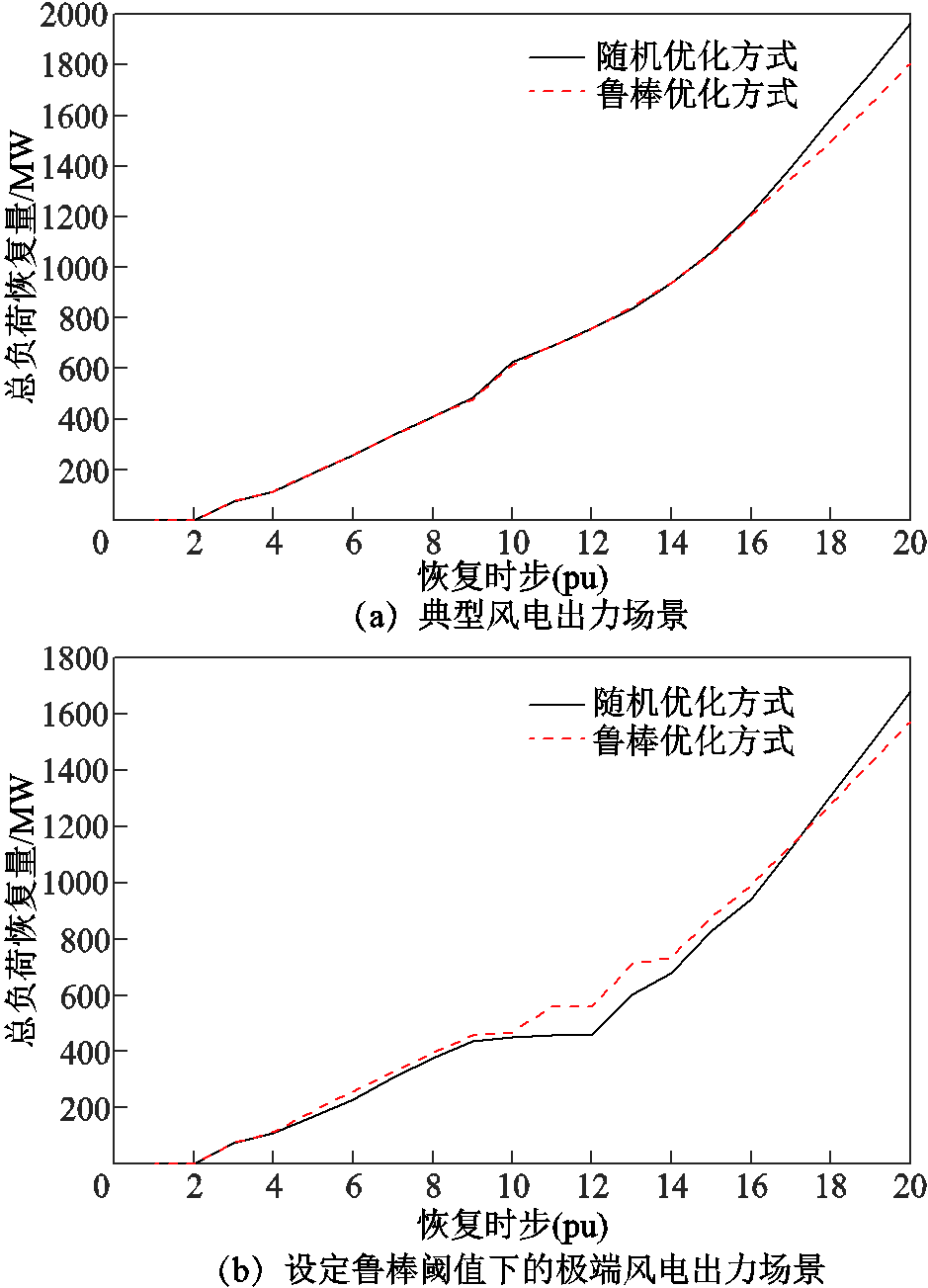
图10 随机与鲁棒优化方法的负荷恢复总量比较
Fig.10 Comparision of total load restoration amount between stochastic and robust optimizaiton methods
图10a中,典型风电出力场景下,应用随机优化方法所得恢复决策总时域内累计负荷恢复总量为24.49GW·h,高于应用鲁棒优化方法所得累计负荷恢复总量23.77GW·h。图10b中,设定鲁棒阈值下的极端风电出力场景下,应用鲁棒优化方法所得恢复决策总时域内累计负荷恢复总量20.22GW·h高于应用随机优化方法所得累计负荷恢复总量19.54GW·h。虽然在恢复决策总时域末,随机优化所得负荷恢复总量高于鲁棒优化,但4~17时步,鲁棒优化所得负荷恢复总量却高于随机优化。由于优化目标为恢复决策总时段内的累积负荷恢复总量,因此,随机优化所得元件恢复次序应用于典型风电出力场景的效果好于鲁棒优化方法,而对于设定鲁棒阈值下的极端风电出力场景则恰恰相反。
为进一步说明鲁棒优化所得元件恢复次序较随机优化对极端风电出力场景的适应性,取理论上的最极端风电波动场景(各时步均取风电预测出力下界),应用上述uro及usto进行长时间尺度恢复模拟,最终得到表2所示的优化结果。可以看出,随机优化所得usto并不适应于理论上的最极端风电波动场景,而鲁棒优化所得uro在理论上的最极端风电波动场景下依旧可行。
表2 基于uro及usto所得优化结果
Tab.2 Optimization results based on uro and usto

优化方法累计负荷恢复总量/(GW·h) 鲁棒优化19.47 随机优化不可解
为进一步验证本文所提方法对含风电实际系统恢复决策的有效性,采用某省实际电网算例,包含52个厂站、9台发电机、80条线路(多回线路已归算为单回线路),实际拓扑如附图3所示。恢复总时步T选定为30,时步长同样设定为10min。JHF、JHD为两处具有黑启动能力的发电厂;JLC的最大启动时限为10个时步;JXX的最小起动时限为10个时步;其余非黑启动电厂的最大起动时限均为30个时步。节点JYS、JHS、JWX、JYZ、JLZ、JSB、JJZ处共有7座风电场,风功率预测偏差取为预测值的0.5倍,不确定预算参数ΓW和ΓT分别取为5、15。主子问题迭代收敛阈值取为0.01。
通过主子问题的反复求解,最终经过2次迭代,(UB-LB)/LB收敛到0.001。迭代过程见表3。
表3 迭代上界和下界
Tab.3 Upper and lower bound during iteration process
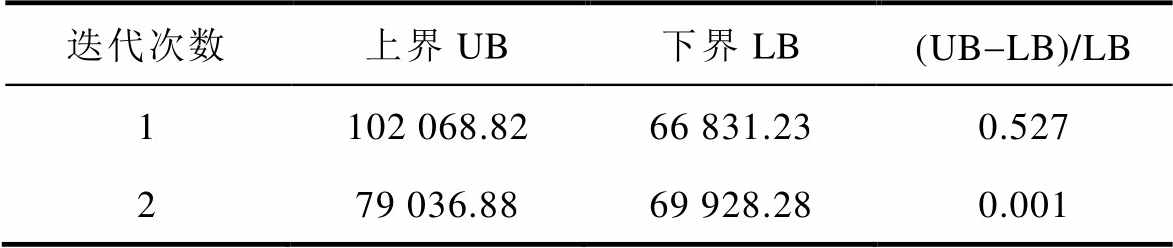
迭代次数上界UB下界LB(UB-LB)/LB 1102 068.8266 831.230.527 279 036.8869 928.280.001
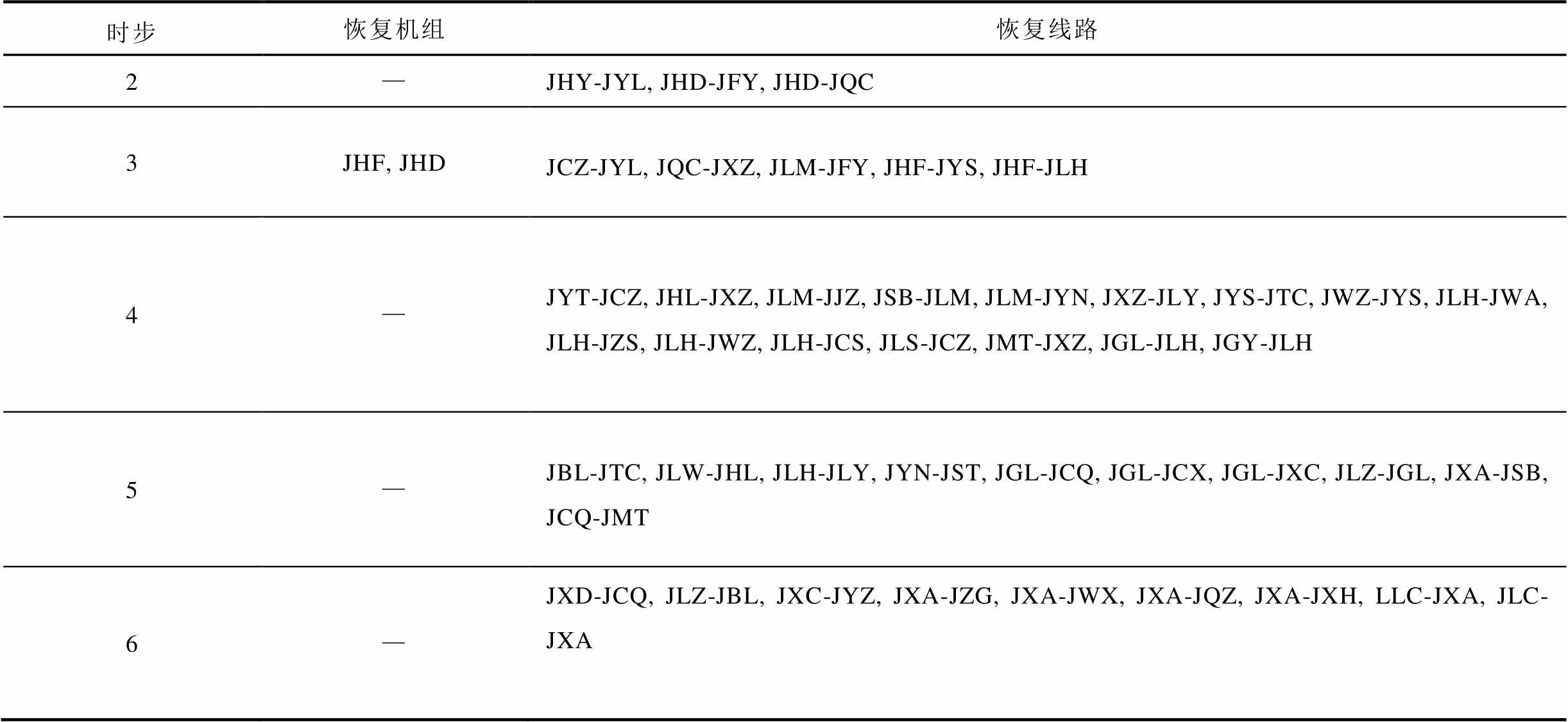
考虑风电预测误差后实际电网的机组、线路恢复顺序见表4。
表4 实际系统机组、线路恢复顺序
Tab.4 Units and lines restoration seqeunce of actual system
时步恢复机组恢复线路 2—JHY-JYL, JHD-JFY, JHD-JQC 3JHF, JHDJCZ-JYL, JQC-JXZ, JLM-JFY, JHF-JYS, JHF-JLH 4—JYT-JCZ, JHL-JXZ, JLM-JJZ, JSB-JLM, JLM-JYN, JXZ-JLY, JYS-JTC, JWZ-JYS, JLH-JWA, JLH-JZS, JLH-JWZ, JLH-JCS, JLS-JCZ, JMT-JXZ, JGL-JLH, JGY-JLH 5—JBL-JTC, JLW-JHL, JLH-JLY, JYN-JST, JGL-JCQ, JGL-JCX, JGL-JXC, JLZ-JGL, JXA-JSB, JCQ-JMT 6—JXD-JCQ, JLZ-JBL, JXC-JYZ, JXA-JZG, JXA-JWX, JXA-JQZ, JXA-JXH, LLC-JXA, JLC-JXA
(续)
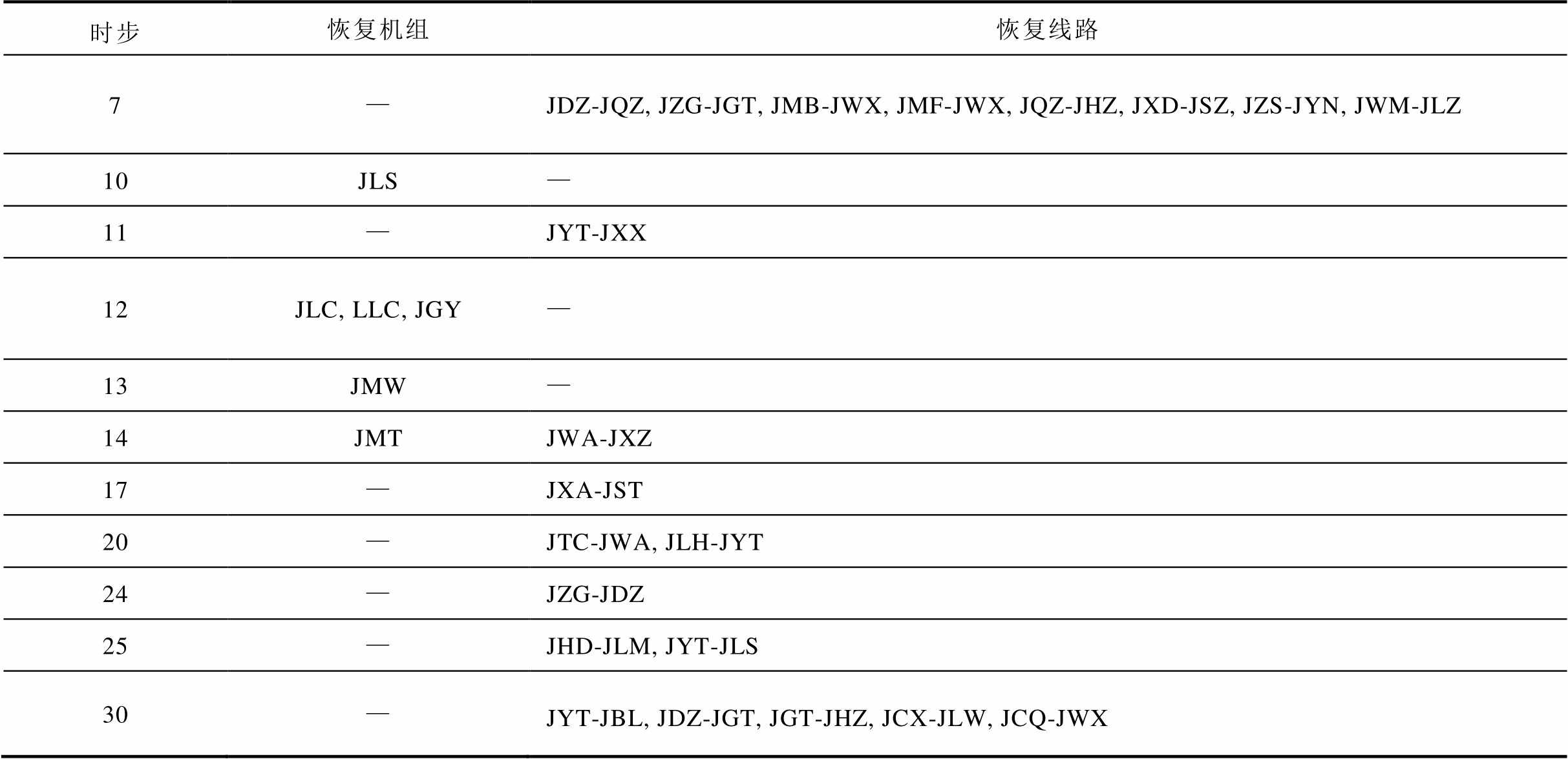
时步恢复机组恢复线路 7—JDZ-JQZ, JZG-JGT, JMB-JWX, JMF-JWX, JQZ-JHZ, JXD-JSZ, JZS-JYN, JWM-JLZ 10JLS— 11—JYT-JXX 12JLC, LLC, JGY— 13JMW— 14JMTJWA-JXZ 17—JXA-JST 20—JTC-JWA, JLH-JYT 24—JZG-JDZ 25—JHD-JLM, JYT-JLS 30—JYT-JBL, JDZ-JGT, JGT-JHZ, JCX-JLW, JCQ-JWX
根据表4可知,在第10,12~14时步,被起动机组陆续起动;在2~7时步,大部分线路陆续恢复;在t=4(pu)时,风电场JJZ、JWZ、JYN、JZS开始向系统提供恢复功率;在5, 7时步,风电场JLY、JHZ、JSZ陆续被恢复。
根据得到的元件恢复次序优化结果以及风电出力典型场景集可以得到实际系统的厂站恢复方案。图11展示了优化所得各时步负荷恢复总量以及风电场总调度出力。
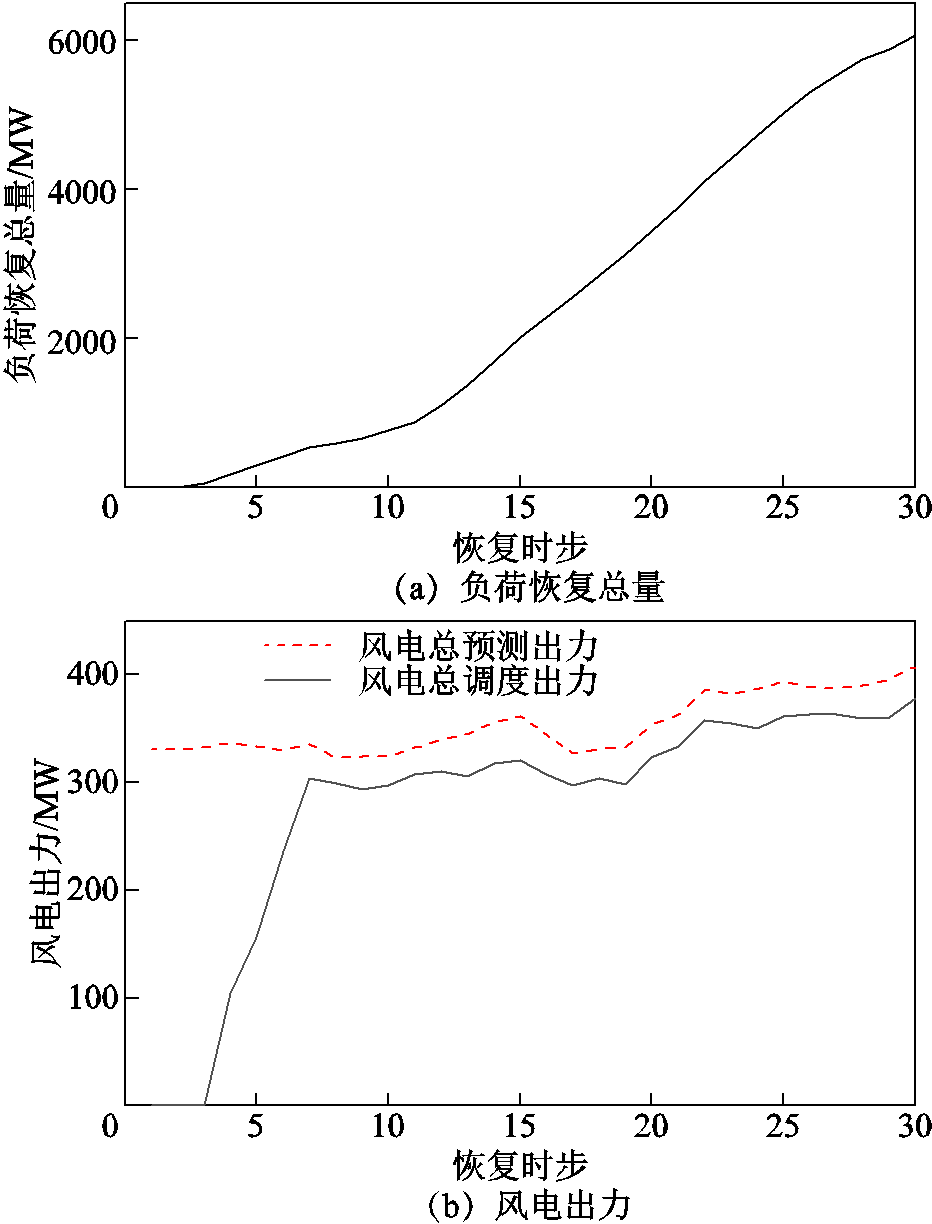
图11 各时步负荷恢复总量以及风电场总调度出力
Fig.11 Total load restoration amount and wind power output in each time step
大停电后的系统恢复涉及多个恢复时步的协调统筹,在恢复准备阶段做好全过程的恢复计划对后续恢复操作具有重要指导意义。为制定适应于规模风电接入的全过程恢复方案,本文基于全过程恢复策略与两阶段鲁棒优化方法,建立了考虑风功率预测误差的全过程鲁棒优化恢复模型。模型包含两个阶段:第一阶段确定元件恢复次序;第二阶段产生风功率最恶劣波动场景集,采用C&CG算法迭代求解。最后,通过39节点系统与某省电网实际系统对所建模型和所提方法进行了验证,得到以下结论:
1)考虑风功率预测误差的两阶段鲁棒恢复模型能够得到不确定预算范围内的元件恢复次序,在此基础上结合风电出力典型场景,能够得到具体的厂站恢复方案。
2)与局部最小生成树搜索以及贪婪搜索这两种典型的恢复决策方式相比,本文全过程建模方式能得到给定恢复目标下的最优恢复方案。
3)在全过程恢复建模方式下,本文两阶段鲁棒优化较随机优化所得元件恢复次序对极端风电波动场景的鲁棒性更强。
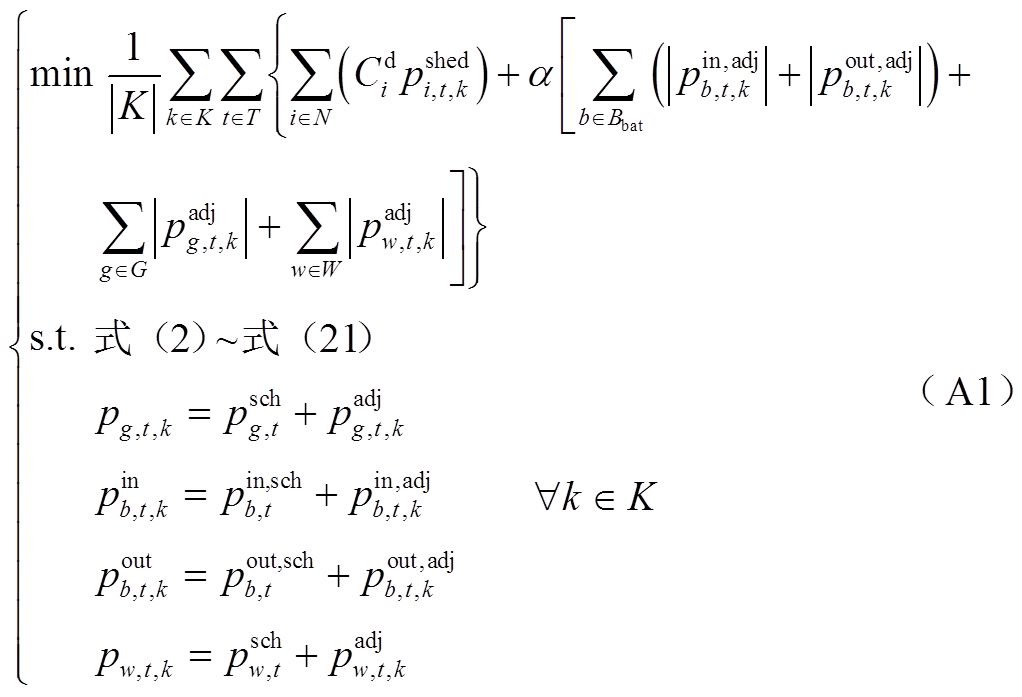
式中,K为典型场景集合;|K|为典型场景数;α为表征功率调节的代价成本,取值越大,代价成本越高;pg,t,k为场景k下发电厂g在时步t的恢复出力;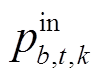 、
、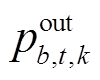 分别为场景k下储能电站b在时步t的充、放电功率;
分别为场景k下储能电站b在时步t的充、放电功率;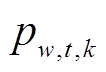 为场景k下风电场w在时步t的输出功率;
为场景k下风电场w在时步t的输出功率;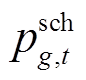 、
、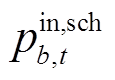 、
、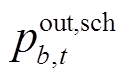 、
、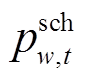 为制定长时间尺度厂站恢复计划需要确定的恢复功率;
为制定长时间尺度厂站恢复计划需要确定的恢复功率;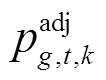 、
、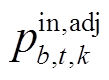 、
、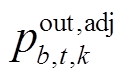 、
、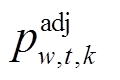 为厂站功率调节量。
为厂站功率调节量。
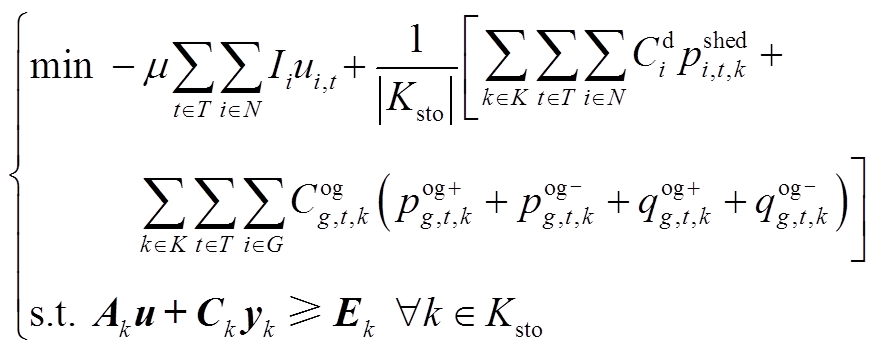 (A2)
(A2)
式中,Ksto为随机优化典型场景集;Ak、Ck、Ek为基于典型场景集的系数矩阵。

附图1 IEEE-39节点系统拓扑
App.Fig.1 IEEE-39 bus system topology
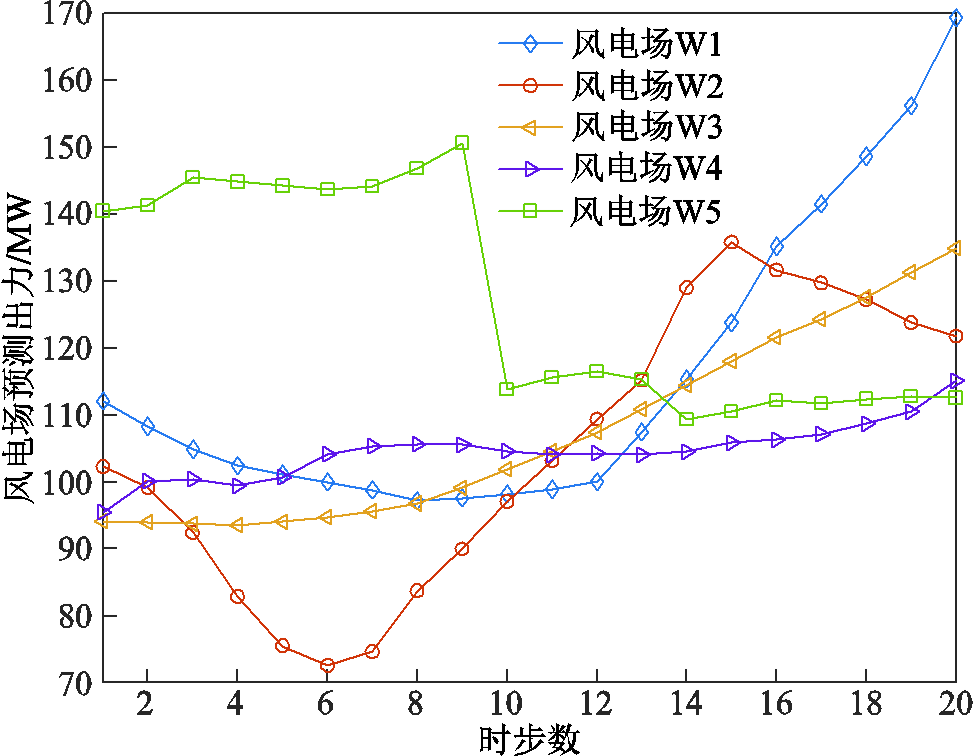
附图2 风电场预测出力
App.Fig.2 Predicted wind power output
附表1 IEEE-39节点发电机数据
App.Tab.1 IEEE-39 bus generator data
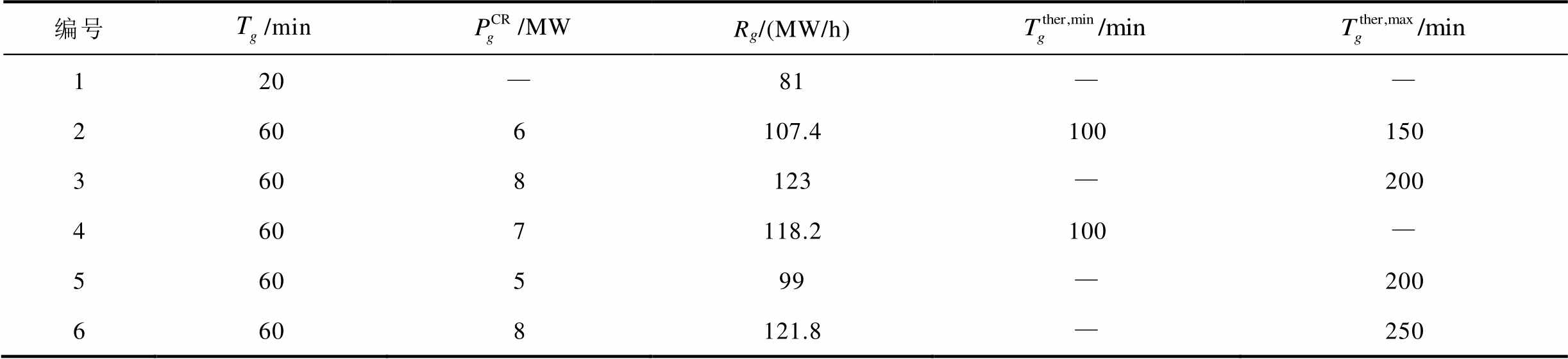
编号/min/MWRg/(MW/h) 120—81—— 2606107.4100150 3608123—200 4607118.2100— 560599—200 6608121.8—250
(续)

编号/min/MWRg/(MW/h)/min/min 7606106.8—250 8606105—200 96013172.8—— 106015192——
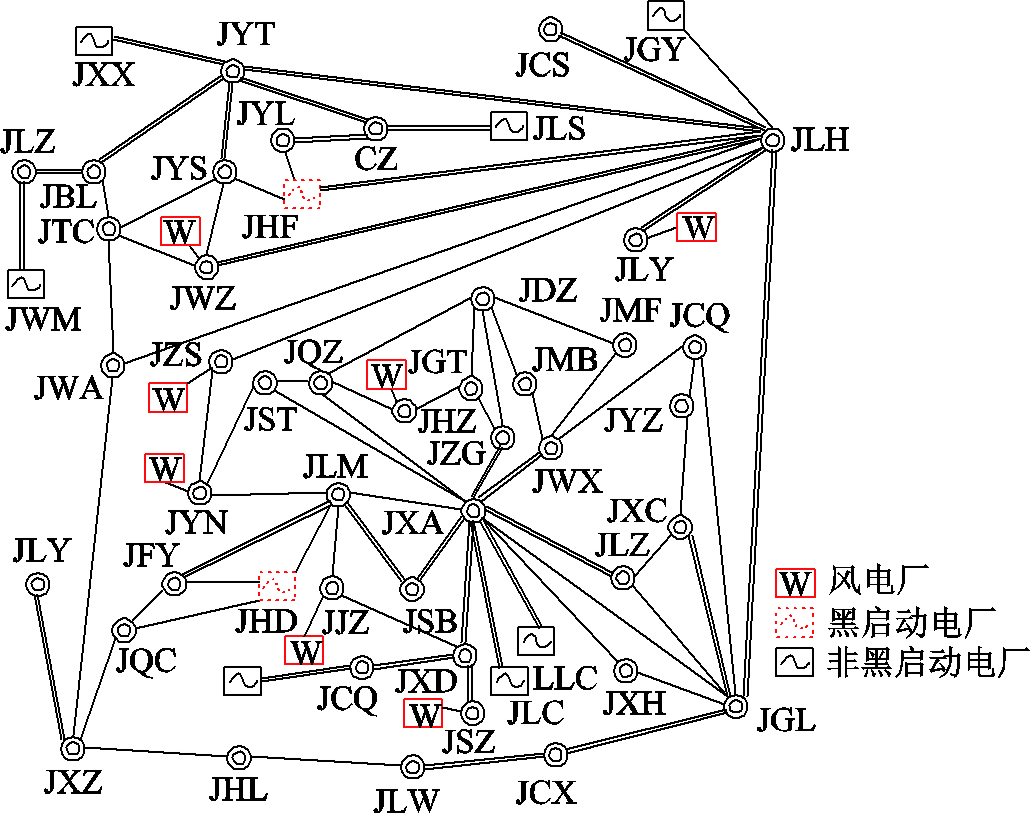
附图3 实际系统拓扑
App.Fig.3 Actual system topology
参考文献
[1] 曾辉, 孙峰, 李铁, 等. 澳大利亚“9·28”大停电事故分析及对中国启示[J]. 电力系统自动化, 2017, 41(13): 1-6.
Zeng Hui, Sun Feng, Li Tie, et al. Analysis of “9·28” blackout in south Australia and its enlightenment to China[J]. Automation of Electric Power Systems, 2017, 41(13): 1-6.
[2] 孙华东, 许涛, 郭强, 等. 英国“8·9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192.
Sun Huadong, Xu Tao, Guo Qiang, et al. Analysis on blackout in great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[3] 严道波, 文劲宇, 杜治, 等. 2021年得州大停电事故分析及其对电网规划管理的启示[J]. 电力系统保护与控制, 2021, 49(9): 121-128.
Yan Daobo, Wen Jinyu, Du Zhi, et al. Analysis of Texas blackout in 2021 and its enlightenment to power system planning management[J]. Power System Protection and Control, 2021, 49(9): 121-128.
[4] 周云海, 闵勇. 恢复控制中的系统重构优化算法研究[J]. 中国电机工程学报, 2003, 23(4): 67-70, 188.
Zhou Yunhai, Min Yong. Optimal algorithm for system reconstruction[J]. Proceedings of the CSEE, 2003, 23(4): 67-70, 188.
[5] 刘威鹏, 刘玉田. 基于非对称Copula函数的风电场黑启动储能优化配置[J]. 电力系统自动化, 2020, 44(19): 47-54.
Liu Weipeng, Liu Yutian. Optimal configuration of energy storage for wind farm black-start based on asymmetric Copula function[J]. Automation of Electric Power Systems, 2020, 44(19): 47-54.
[6] 李军徽, 尤宏飞, 李翠萍, 等. 基于模型预测控制的风光储黑启动功率协调策略[J]. 电网技术, 2020, 44(10): 3700-3708.
Li Junhui, You Hongfei, Li Cuiping, et al. Power coordination strategy based on model predictive control for black start with PV-wind-battery system[J]. Power System Technology, 2020, 44(10): 3700-3708.
[7] 刘昌盛, 谢云云, 王晓丰, 等. 基于IGDT的网架重构过程中风电场出力调度[J]. 电力工程技术, 2019, 38(3): 27-33.
Liu Changsheng, Xie Yunyun, Wang Xiaofeng, et al. IGDT based power dispatch for wind farms participating in power system restoration[J]. Electric Power Engineering Technology, 2019, 38(3): 27-33.
[8] 周宜昌, 刘艳, 顾雪平. 考虑多风电场黑启动价值的机组恢复顺序双层优化决策[J]. 电力系统自动化, 2020, 44(16): 87-97.
Zhou Yichang, Liu Yan, Gu Xueping. Bi-level optimization decision for unit recovery sequence considering black-start value of multiple wind farms[J]. Automation of Electric Power Systems, 2020, 44(16): 87-97.
[9] 赵瑾, 王洪涛, 曹曦. 计及风电条件风险价值的负荷恢复双层优化[J]. 中国电机工程学报, 2017, 37(18): 5275-5285, 5526.
Zhao Jin, Wang Hongtao, Cao Xi. Bi-level optimization of load restoration considering the conditional value at risk of wind power[J]. Proceedings of the CSEE, 2017, 37(18): 5275-5285, 5526.
[10] 顾雪平, 周光奇, 李少岩, 等. 考虑风电预测误差相关性的负荷恢复鲁棒优化[J]. 电网技术, 2021, 45(10): 4092-4104.
Gu Xueping, Zhou Guangqi, Li Shaoyan, et al. Robust optimization of load restoration scheme considering wind power prediction error correlation[J]. Power System Technology, 2021, 45(10): 4092-4104.
[11] Sun Wei, Liu C C, Zhang Li. Optimal generator start-up strategy for bulk power system restoration[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1357-1366.
[12] Liu Yan, Gu Xueping. Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization[J]. IEEE Transactions on Power Systems, 2007, 22(3): 1267-1274.
[13] 王洪涛, 刘玉田, 邱夕兆, 等. 基于多agent的电力系统主从递阶恢复决策[J]. 电力系统自动化, 2006, 30(15): 5-9.
Wang Hongtao, Liu Yutian, Qiu Xizhao, et al. Multi-agent based Stackelberg decision for power system restoration[J]. Automation of Electric Power Systems, 2006, 30(15): 5-9.
[14] Golshani A, Sun Wei, Zhou Qun, et al. Incorporating wind energy in power system restoration planning[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 16-28.
[15] 徐秋实, 邓长虹, 赵维兴, 等. 含风电电力系统的多场景鲁棒调度方法[J]. 电网技术, 2014, 38(3): 653-661.
Xu Qiushi, Deng Changhong, Zhao Weixing, et al. A multi-scenario robust dispatch method for power grid integrated with wind farms[J]. Power System Technology, 2014, 38(3): 653-661.
[16] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467.
Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.
[17] 张雨曼, 刘学智, 严正, 等. 光伏-储能-热电联产综合能源系统分解协调优化运行研究[J]. 电工技术学报, 2020, 35(11): 2372-2386.
Zhang Yuman, Liu Xuezhi, Yan Zheng, et al. Decomposition-coordination based optimization for PV-BESS-CHP integrated energy systems[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2372-2386.
[18] 蔡瑶, 卢志刚, 孙可, 等. 计及源荷不确定性的独立型交直流混合微网多能源协调优化调度[J]. 电工技术学报, 2021, 36(19): 4107-4120.
Cai Yao, Lu Zhigang, Sun Ke, et al. Multi-energy coordinated optimal scheduling of isolated AC/DC hybrid microgrids considering generation and load uncertainties[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4107-4120.
[19] 曹曦, 王洪涛. 大规模电网源荷协调恢复决策与控制方法[J]. 中国电机工程学报, 2017, 37(6): 1666-1675.
Cao Xi, Wang Hongtao. Source-load coordinated restoration decision-making and control method for large scale power system[J]. Proceedings of the CSEE, 2017, 37(6): 1666-1675.
[20] 王亮, 刘艳, 顾雪平, 等. 综合考虑节点重要度和线路介数的网络重构[J]. 电力系统自动化, 2010, 34(12): 29-33.
Wang Liang, Liu Yan, Gu Xueping, et al. Skeleton-network reconfiguration based on node importance and line betweenness[J]. Automation of Electric Power Systems, 2010, 34(12): 29-33.
[21] 朱冬雪, 顾雪平, 钟慧荣. 电力系统大停电后机组恢复的多目标优化方法[J]. 电网技术, 2013, 37(3): 814-820.
Zhu Dongxue, Gu Xueping, Zhong Huirong. A multi-objective optimization method for post-blackout unit restoration[J]. Power System Technology, 2013, 37(3): 814-820.
[22] Yang Jingwei, Zhang Ning, Kang Chongqing, et al. A state-independent linear power flow model with accurate estimation of voltage magnitude[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3607-3617.
[23] 叶畅, 曹侃, 丁凯, 等. 基于广义储能的多能源系统不确定优化调度策略[J]. 电工技术学报, 2021, 36(17): 3753-3764.
Ye Chang, Cao Kan, Ding Kai, et al. Uncertain optimal dispatch strategy based on generalized energy storage for multi-energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3753-3764.
[24] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804.
Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1791-1804.
[25] Bertsimas D, Litvinov E, Sun X A, et al. Adaptive robust optimization for the security constrained unit commitment problem[J]. IEEE Transactions on Power Systems, 2013, 28(1): 52-63.
[26] 曾顺奇, 文福拴, 薛禹胜, 等. 计及操作时间不确定性的电力系统网架重构策略优化[J]. 电力系统自动化, 2011, 35(23): 16-21.
Zeng Shunqi, Wen Fushuan, Xue Yusheng, et al. Optimization of network reconfiguration strategy for power systems considering operating time uncertainty[J]. Automation of Electric Power Systems, 2011, 35(23): 16-21.
[27] 刘伟佳, 林振智, 文福拴, 等. 计及重要负荷优先恢复的局部电力系统恢复策略[J]. 电力系统自动化, 2013, 37(12): 31-37.
Liu Weijia, Lin Zhenzhi, Wen Fushuan, et al. A restoration strategy for a local power system considering critical load pickup[J]. Automation of Electric Power Systems, 2013, 37(12): 31-37.
[28] 刘强, 石立宝, 倪以信, 等. 电力系统恢复控制的网络重构智能优化策略[J]. 中国电机工程学报, 2009, 29(13): 8-15.
Liu Qiang, Shi Libao, Ni Yixin, et al. Intelligent optimization strategy of the power grid reconfiguration during power system restoration[J]. Proceedings of the CSEE, 2009, 29(13): 8-15.
Two Stage Robust Optimization Method for the Whole-Process Power System Restoration Considering Wind Power Uncertainty
Abstract The proportion of wind power in power systems will be further improved in the process of low carbon transformation in China. It is of great significance to study the restoration control problem under the new situation to improve the security of power systems. Aiming at the problem of power system restoration decision optimization under the background of wind power integration,a two-stage robust optimization model considering wind power uncertainty was established for the whole power system restoration process in this paper. In the first stage, the node-importance index, load restoration amount and wind power fluctuation scenario set were considered to make a decision on power system component restoration sequence. In the second stage, two-level objectives were included. The outer-level objective was to maximum the impact of wind power fluctuation on load restoration. The inner-level objective was to maximum load restoration in the worst wind power fluctuation scenario. The model of the second stage was transformed into a single-level optimization model by the duality principle. The interval uncertainty set was used to depict the temporal and spatial uncertainty of wind power. The two-stage optimization problem was solved by column-and-constraint generation algorithm, and the heuristic method was used to accelerate the first stage solving process. Finally, the robustness and practicability of the proposed method are verified by the New England 39-bus system and a real power system.
keywords:Blackout, restoration control, whole-process, robust optimization, column-and- constraint generation
DOI:10.19595/j.cnki.1000-6753.tces.211148
中图分类号:TM732
国家自然科学基金(52107092)、河北省自然科学基金(E2019502195)和中央高校基本科研业务费专项资金(2021MS063)资助项目。
收稿日期 2021-07-27
改稿日期 2022-02-10
顾雪平 男,1964年生,教授,博士生导师,研究方向为电力系统安全防御和系统恢复、安全稳定评估与控制、智能技术在电力系统中的应用等。E-mail:xpgu@ncepu.edu.cn
白岩松 男,1997年生,博士研究生,研究方向为电力系统安全防御和恢复控制。E-mail:2846919603@qq.com(通信作者)
(编辑 李冰)