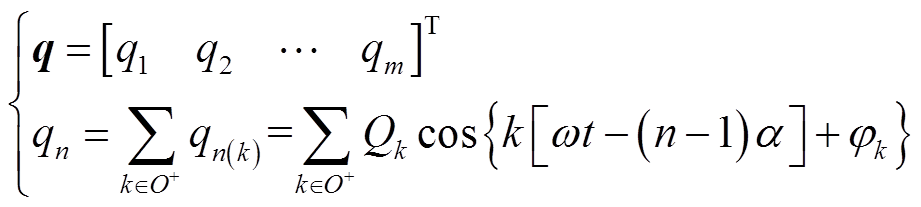（1）
摘要 多相电机驱动系统可靠性高、容错能力强、控制灵活。该文对断相容错运行下，多相电机中低频奇数次电流谐波的特性和补偿方法进行了研究。利用广义Clarke变换，可将电机定子电流变换到各个子空间当中。研究发现，断相容错时，各次谐波电流以正负序分量同时存在的形式分布在所有子空间当中。传统谐波补偿方法只在特定子空间下进行补偿，在断相容错工况下性能有较大恶化。该文提出一种改进电流谐波补偿方法，利用广义对称分量变换和正负序PI控制器实现各子空间内正负序谐波电流补偿，保证了断相容错时良好的补偿效果。在九相感应电机平台上对提出方法进行验证，实现了断相容错时对选定电流谐波的完全补偿，并降低了谐波带来的额外损耗和转矩脉动。
关键词：多相电机 断相故障 容错控制 电流控制 谐波补偿
多相电机调速系统有可靠性高、功率容量大、转矩脉动低、器件容量要求低和控制灵活等优点，还可利用额外自由度实现容错控制和谐波电流控制[1-2]，已成为研究和产业应用的焦点，在舰船电力推进、多电飞机以及电动汽车等都有一定的应用[1-3]。
容错控制是当前研究热点。大多数电机故障可通过一定方式等效为断相故障[2]，故大多数容错控制方法针对的是断相故障[4-6]。各种容错控制方法中，常要求谐波电流有特定的形式，若定子绕组中存在额外谐波电流，会产生额外铜耗和转矩脉动，使控制性能恶化[7-8]。因此，谐波电流控制对容错控制性能有重要影响。
电压源型逆变器（Voltage Source Inverter, VSI）供电的多相调速系统中，定子电流谐波最主要成分为逆变器和电机非线性（死区、磁饱和等）造成的低频奇数次分量[9]，它们对控制性能有较大影响。正常工况下低频奇数次谐波电流控制方面的研究已成熟[9-11]。但断相时谐波电流特性与控制方面的研究尚不完善[7-8,12-15]。文献[7]中针对对称六相永磁同步电机的3次谐波电流补偿方法进行了研究，但仅适用于单相断相情况，难以拓展到其他断相工况。文献[8]中提出了基于模型预测控制的五相永磁同步电机3次谐波电流补偿方法，但补偿效果一般，在控制频率为10kHz时仅能将3次谐波电流占基波电流的比例减小到2.87%。文献[12-14]在谐波平面采用PR或同步PI控制器对谐波电流进行补偿或者注入，但并未考虑存在于基波平面的谐波电流，而基波平面的谐波电流会引起较大转矩脉动，对容错控制性能有较大影响。文献[15]中向五相永磁同步电机中注入特定谐波电流来抑制故障后转矩脉动，但由于电流控制器构建在自然坐标系中，基波、谐波电流控制存在稳态误差。可见，现有故障容错下谐波电流控制方法存在对参数、工况依赖较大，谐波控制效果较差，未考虑基波平面谐波电流等问题。
为解决现有方法中存在的问题，本文对对称型多相电机断相故障下电流谐波的特性和补偿方法进行了研究。在断相容错情况下，建立了分析电流谐波的等效模型，结果表明：故障时，在所有子空间中，各次谐波电流正负序分量同时存在。正常工况，某次谐波电流只以特定序分量的形式存在于某特定子空间中，传统补偿方法只考虑此分量，无法对容错运行时的额外分量进行抑制，补偿效果恶化程度较高。根据断相时谐波电流特性，本文提出一种改进谐波电流补偿方法。利用广义对称分量变换，将各次谐波电流变换为互相独立的对称分量，采用正负序PI控制器进行补偿。在九相异步电机上对所提方法进行实验验证，结果表明，所提方法可在多种故障工况下实现更好的容错控制性能和谐波补偿效果。与传统方法相比，所提方法可将选定谐波有效值占基波有效值的比例从15.72%降低至0.6%，在故障工况下可保证优异的补偿性能。
需要注意的是，本文为了使理论推导更加简洁，将研究对象限定为具有一个中性点的对称型多相电机，但本文的理论推导思路、结论以及控制方法具有通用性，不仅适用于非对称型多相电机，也能适应具有不同中性点数量和相数的情况。只要选择了适当的广义对称分量变换矩阵，就可以很容易地将所提方法移植到有不同相数和定子绕组配置的多相电机系统中。
一个VSI供电的m相对称型多相电机，若逆变器和电机完全对称，电机定子各电量瞬时值表达式为[9]
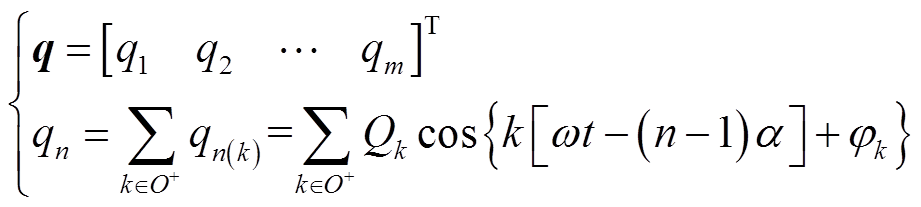（1）
式中，q代表任何相电量，如相电流i、相电压u和相反电动势e等；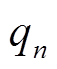
为第n相的瞬时电量，n为1到m的整数；k为谐波次数，O+为所有正奇数组成的集合；qn(k)为qn中的第k次谐波分量；
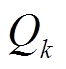和
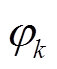为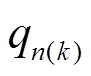
的幅值与初相位；ω为基波角频率；t为时间；α为相邻两相绕组的空间位置差，α=2π/m。
对称型多相电机可通过变换到多个子空间中进行建模，其中自由度为2的子空间个数为ns=floor((m-nnp)/2)，nnp为电机中性点个数，m-nnp为偶数时，自由度为2的子空间下的模型可完全决定电机运行特性。当m-nnp为奇数时，需再定义一个单自由度子空间才能完全决定电机运行特性[9]。子空间的选择并不是唯一的，一种常用方式为选择奇数次子空间αβs，其中s≠μ(m/nnp)，μ为任意正整数[16]。对应αβs的变换矩阵为Ts，用Ts乘以相矢量q，可得到映射至αβs子空间下的复矢量qαβ(s)，即[6]
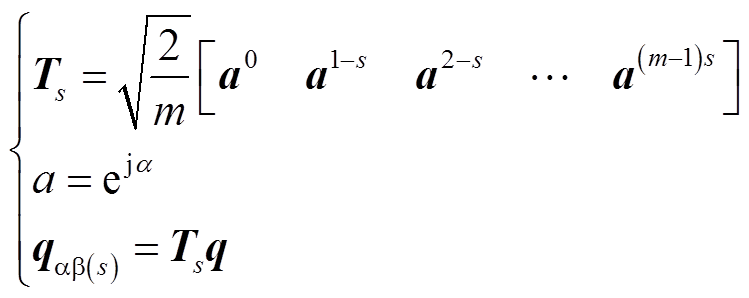（2）
将式（1）代入式（2），可得
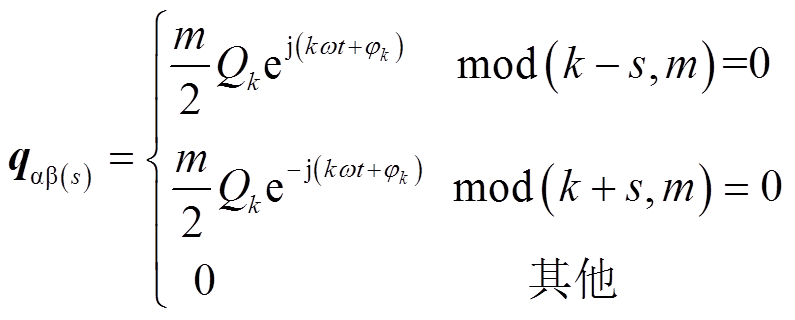（3）
式中，mod(a,b)为整数a、b相除后的余数。由式（3），只有k+s或k-s为m的整数倍时，k次谐波才能映射到αβs中[6]。
由于正常工况下，根据式（3），低频k次谐波电流（k＜m，k为奇数）仅会被映射到αβk中，两种传统的补偿方法仅在αβk中进行补偿，正常工况下两种常用的谐波补偿方法如图1所示[17]。第一种传统方法利用k次谐波的旋转坐标变换，将αβk中k次谐波电流变换到k次正序旋转坐标系下，并采用PI控制器进行调节，其中θr是αβ1中转子磁链位置角，idq(k)(+k)是变换到k次正序旋转坐标系中的定子电流矢量，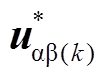
是αβk中的定子端电压参考值。第二种传统方法则直接在静止的αβk中，采用谐振频率等于k次谐波频率的PR控制器直接对谐波电流进行控制。
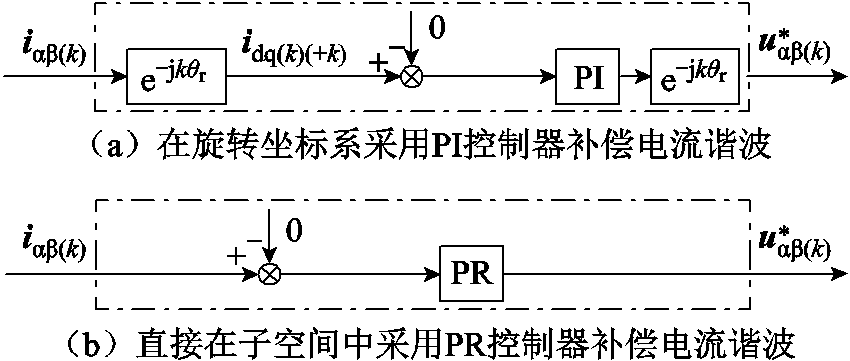
图1 正常工况下两种常用的谐波补偿方法
Fig.1 Two commonly used current harmonic compensation methods in the healthy condition
断相情况下的相电流不再是式（1）的形式，断相相电流为零。基波相电流由使用的优化策略决定[2]，有式（4）的形式。
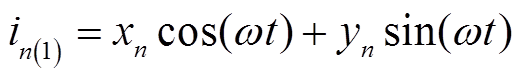（4）
式中，xn和yn为第n相中的余弦和正弦分量的幅值。断相相的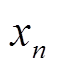
和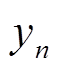
均为0。为保证αβ1中的基波电流矢量轨迹为圆形，相电流须满足约束
（5）
同时，x和y须满足定子绕组联结方式施加的约束[6]。在定子中仅存在基波电流时，可以得到由基波电流产生的磁动势为
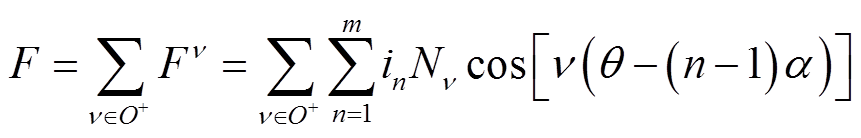（6）
式中，F为定子磁动势；Fn为定子n次空间磁动势；Nn为n次空间谐波的每相等效串联匝数；θ为定子空间位置电角度。将式（5）代入式（6），可得
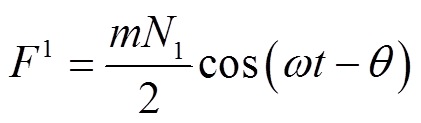（7）
由于磁饱和等非线性特性，由F1产生的空间磁通密度B1中包含空间谐波，但B1在空间中旋转的速度与F1一致，因此B1的表达式为
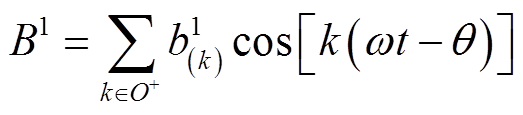（8）
式中，
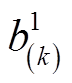为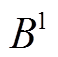
的k次空间谐波的幅值。第n相中，由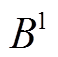感应的相反电动势的表达式为
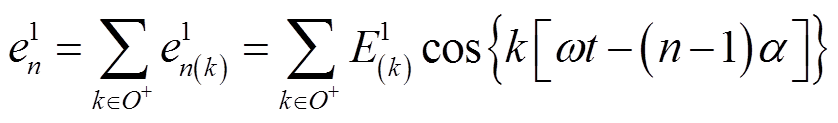（9）
式中，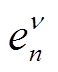
为第n相中Fn感应出的反电动势；
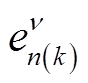为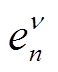中的k次谐波；
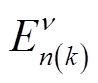为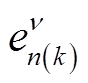的幅值。根据式（9），断相容错时，由
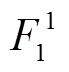产生的反电动势谐波具有与正常运行时的式（1）相似的形式。
对于式（6）中n≠1的部分，正常工况下，当1±n不为m的整数倍时，Fn=0。但在断相容错时，Fn≠0。将式（4）代入式（6）， Fn表达式为
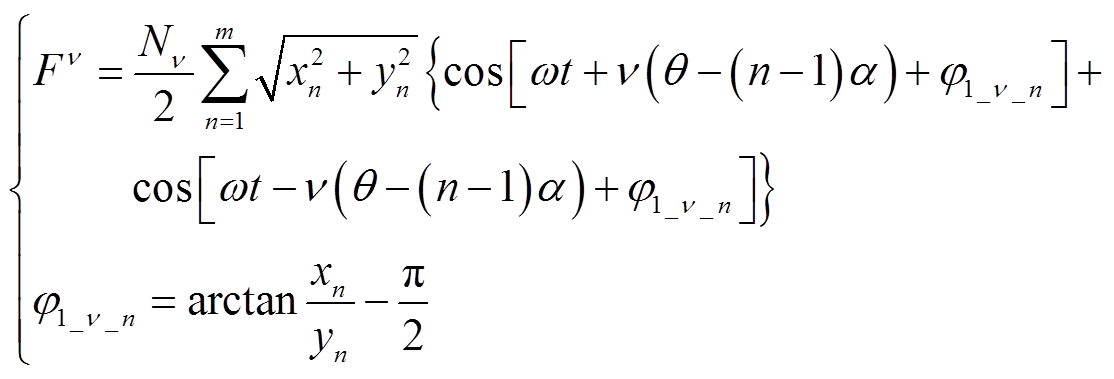（10）
与从式（7）～式（9）的推导类似，可得到Fn感应的相反电动势为
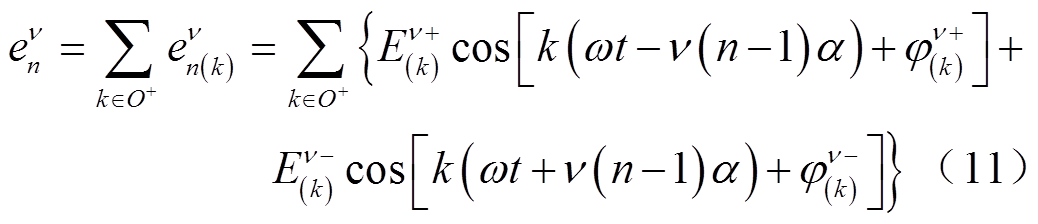
式中，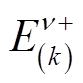
和
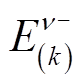分别为正、负序k次谐波相反电动势的幅值；
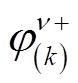和
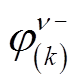分别为正、负序k次谐波相反电势的初相位。根据叠加定理，将式（9）和式（11）中的相反电动势分量相加，可以得到各相中的反电动势为
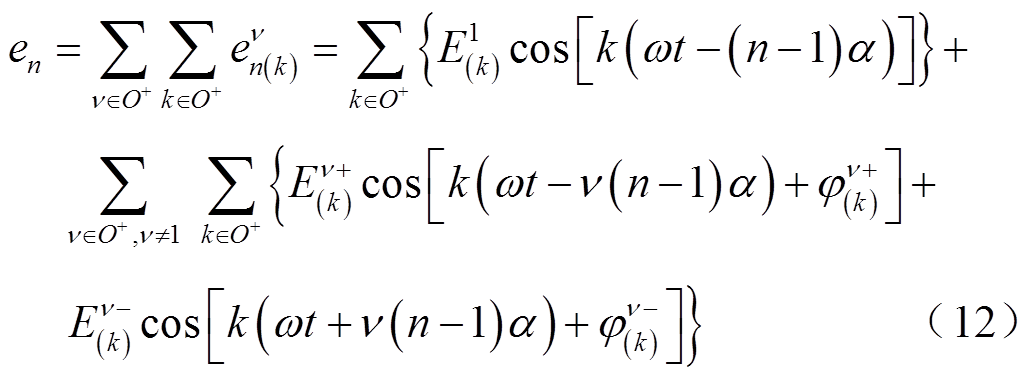
式中，第二个求和符号内(n-1)α的系数不再是1，与式（1）不同。这说明式（3）中的正常工况下反电动势谐波映射情况在断相故障情况下不再适用。
VSI供电时，端电压谐波主要由开关器件死区造成[18]。虽有研究者提出了很多死区补偿方法，但其性能受电流极性判断影响较大，且在电流谐波存在情况下性能会恶化[19-20]。因此，多相电机系统中，准确死区补偿的实现较困难。即使可准确地补偿死区，由于反电动势谐波的存在，定子中仍会有谐波电流。与追求高精度死区补偿方案相比，谐波电流补偿算法更易实现且性能更好，故本文不对死区补偿进行讨论。
正常工况时，相电流对称，死区造成的电压畸变也是对称的，定子端电压有式（1）的形式，其在子空间中的映射规律符合式（3）[21]。但是，断相容错时，定子电流不对称，死区电压畸变需进一步研究。
尽管死区效应与电流大小、器件开关速度等因素相关，大多文献中将死区电压畸变建模成由电流极性决定的方波[21]，即
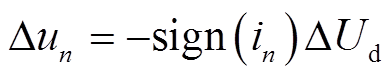（13）
式中，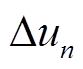
为死区效应在第n相造成的电压畸变；sign(·)为符号函数；
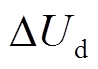为电压畸变量幅值，由死区时间占开关周期比例和直流母线电压决定。在故障状态下，只考虑基波电流，将式（4）代入式（13）并进行傅里叶分解可得到
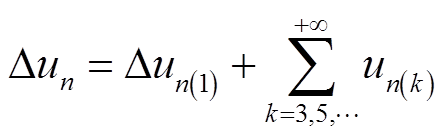（14）
式中，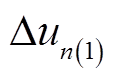
为基波电压的畸变量。可以得到断相故障下第n相端电压中的k次谐波分量为
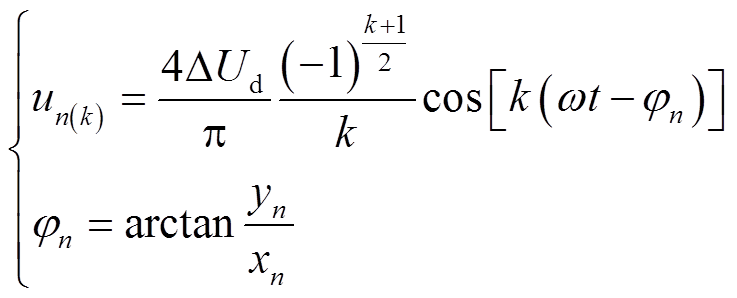（15）
考虑多种可能出现的开路故障，由两电平VSI供电的多相电机系统拓扑示意图如图2所示。图中也展示了开关管开路故障，这种故障在容错控制时，一般会将故障所在桥臂整个封锁，将故障转换为断相故障进行容错控制，因此在容错控制方面与断相故障并无区别。
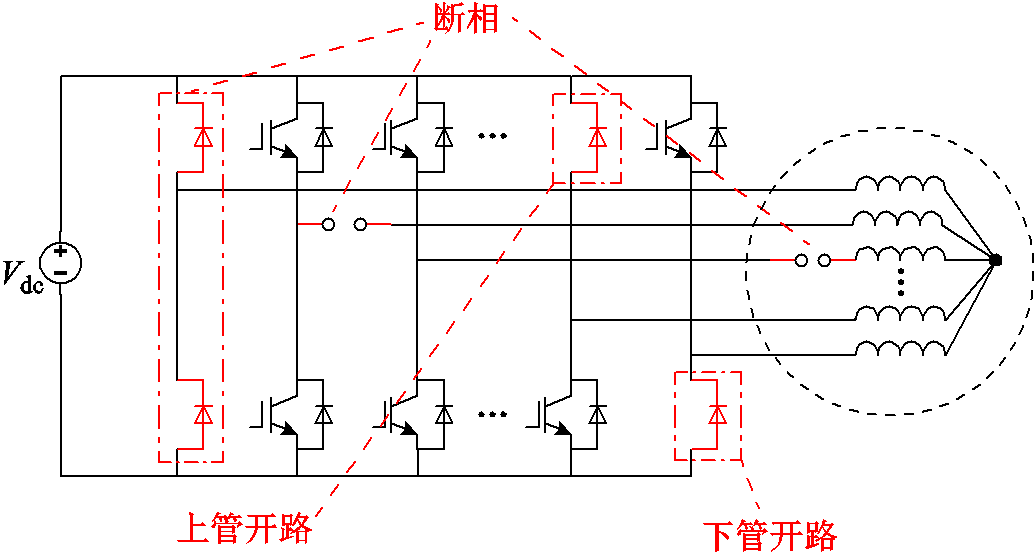
图2 两电平VSI供电的多相电机系统拓扑及其常见开路故障
Fig.2 The topology of a multiphase drive system fed by a two-level VSI and its common open-circuit faults
为研究断相容错时的电流谐波，可以从图2所示拓扑中对断相电机进行抽象，建立断相情况下电机定子等效模型。断相故障下m相电机定子可用图3a表示。图3a中各电压参考点为直流母线中点，u0是电机中性点相对于直流母线中点的电压；图3b中“×”代表断相故障位置，虽然只画出一个“×”，但以下分析适用于多相断相情况。
考虑k次谐波，根据叠加定理，分离出只含k次谐波的等效电路，如图3b所示。可求出每相漏阻抗上的谐波压降为
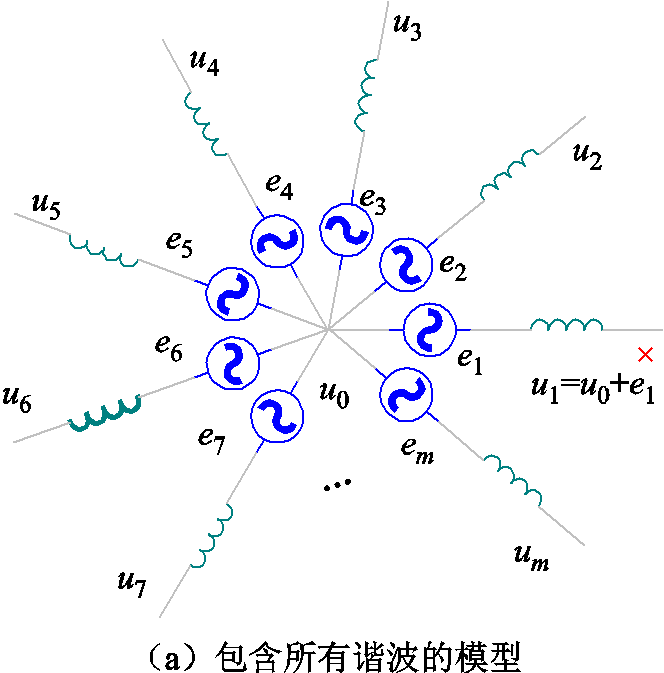
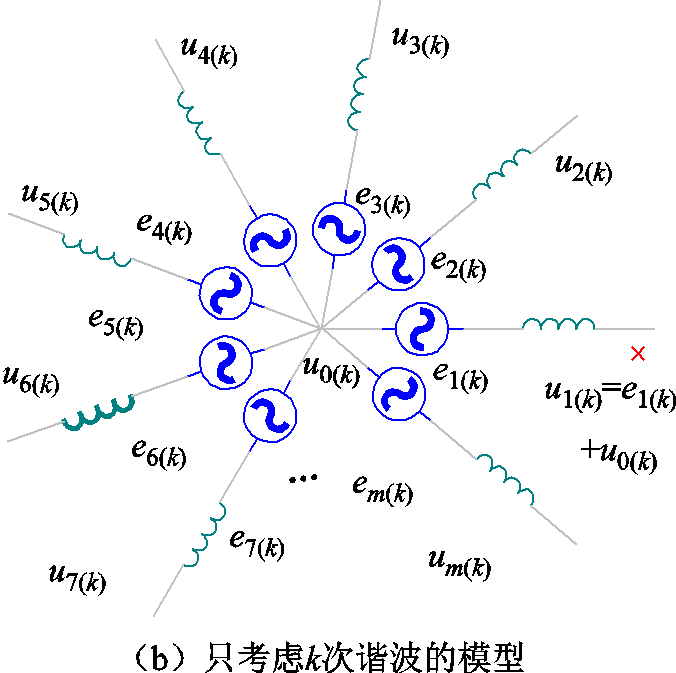
图3 断相故障下电机的等效模型
Fig.3 Equivalent machine models in open-phase conditions
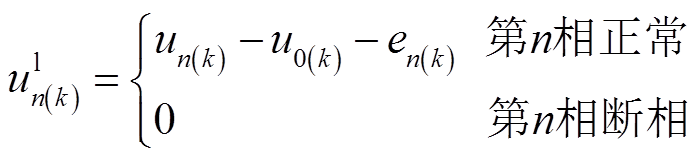（16）
由零序电流约束可得
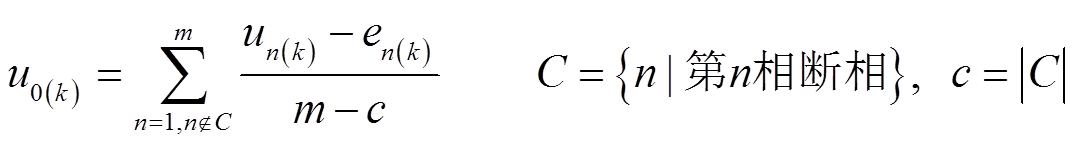（17）
式中，C为发生断相故障相编号组成的集合；c为发生断相故障相的数量。用式（2）将式（17）变换到αβs中，得到漏阻抗k次谐波压降映射到αβs中的电压矢量为
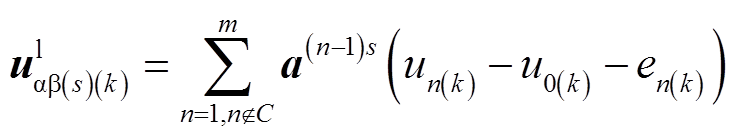（18）
将式（17）代入式（18）得到
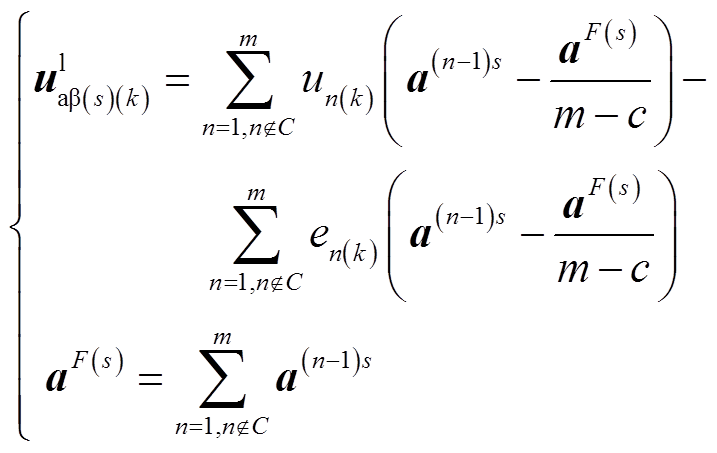（19）
式（19）中第一式等号右侧由两项构成，第一项与端电压谐波有关，第二项则与相反电动势谐波有关。将式（15）代入第一项当中并化简可得
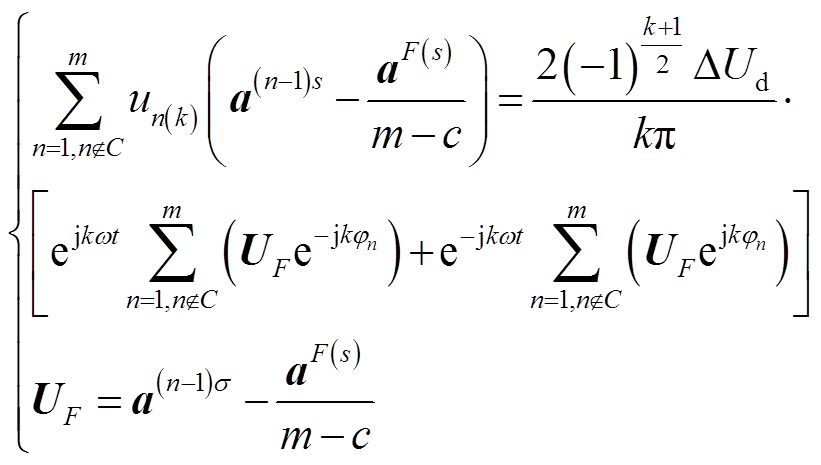（20）
可见，式（20）时含有正序、负序分量，二者幅值、相位与所用电流优化方法和断相故障位置有关。
式（12）所示相电动势形式较复杂，难以直接代入式（19）的第二项进行计算。由于式（12）等号右侧是由对应于不同空间谐波次数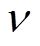
和不同时间谐波次数k的电动势
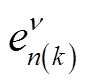项叠加而成，因此只需研究当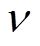和k固定时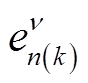的映射情况即可。将式（19）等号右侧第二项当中的en(k)用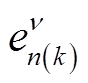代替并整理得到式（21），其中包含正序分量Ep1和Ep2，以及负序分量En1和En2。这四个分量相互间紧密耦合，同时出现。除非各相邻正常相间空间角度差相同（正常相在空间上呈对称分布），为gα(g为整数)，同时满足式（22），式（21）才为零，否则不为零。
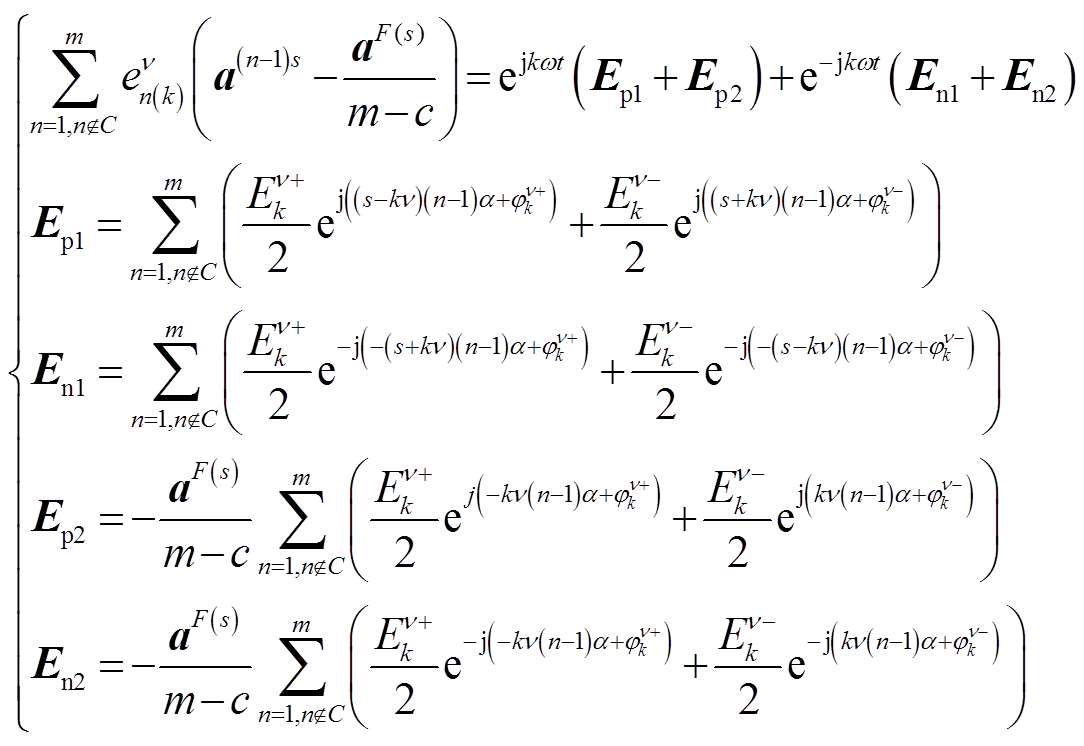（21）
式中，μ1和μ2是任意整数。
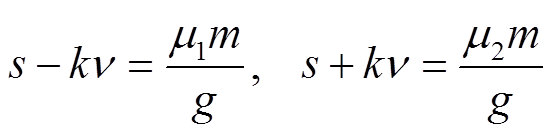（22）
然而，即使针对于某一个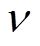，式（22）得到满足，由于在式（12）中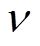可取任意正奇数，总存在某些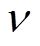的取值使式（22）无法满足，因此在αβs中对于大多数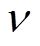的取值，这四个分量均不为零。因此，αβs中必定同时存在正序、负序k次谐波反电动势。
端电压谐波主要与所用的电流优化方法和断相位置相关，而反电动势谐波与电机的电磁设计和负载大小等因素相关，影响二者的因素不同，一般情况下这两种谐波无法相互抵消。因此映射到任一子空间的漏阻抗压降中都同时存在正、负序奇数次谐波分量，如不能对其进行补偿，就会产生正序、负序谐波电流。因此，k次谐波电流将会以正、负序分量同时存在的形式出现在每一个子空间中，不再遵循式（3）。正常情况下和断相故障下谐波电流子空间映射特性上的区别可以总结见表1。
表1 正常情况与断相情况下谐波电流子空间映射特性
Tab.1 Characteristics of harmonics mapping in the healthy condition and open-phase conditions
运行状况谐波次数映射到的子空间序分量性质 正常低频奇数次谐波k，k＜m，k为奇数αβk正序 断相所有子空间正序+负序
文献[22]为分析非对称多相电气网络的稳态特性提出了对称分量法。这种方法在处理三相电网当中的不平衡方面得到了广泛应用[23]。文献[16]提出了广义对称分量法并将其用于对称多相系统的电流均衡控制。文献[5]中，该方法被用来进行断相故障后基波电流的容错控制。本文中，此方法被扩展用于谐波电流控制。
根据文献[16]，k次谐波分量的广义对称分量矩阵为
（23）
式中，Tk, T3k, 
, T(2floor((m-1)/2)-1)k可以通过式（2）计算；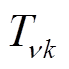
对应k次谐波的第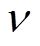个对称分量；Z为对应电机零序分量的变换矢量。
利用式（23）所示矩阵对定子某次谐波电流进行变换，可将其分解成各子空间中相互独立的对称分量，各对称分量可在相应子空间中采用单独的电流控制器控制，从而在断相时实现对于谐波电流的补偿。
根据式（2），Ts、Ts+m和Tm-s对应相同的子空间，可通过将式（23）中的
替换成mod(,m)或m-mod(,m)来对式（23）进行化简，化简后的变换矩阵与基波分量的广义对称分量变换矩阵相同，如式（24）所示。
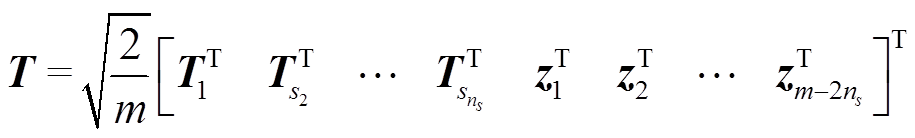（24）
式中，下标1, s2, s3, , 
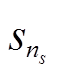为本文1.2节中所选择的各子空间的次数；z1, z2, , 
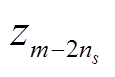为由电机相数和中性点连接方式决定的零序分量变换矢量[24]。因此，只使用式（24）这一个变换矩阵即可实现对于所有谐波次数对称分量的提取，降低了计算量。
本文基于广义对称分量法提出了k次电流谐波的补偿方法，如图4所示。图中的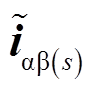
为αβs中电流指令与实际电流之差；PR(k)为谐振频率对应k次谐波的比例谐振控制器；
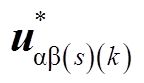为αβs中k次谐波电压参考值。在各子空间中利用正、负序旋转坐标变换，将谐波电流正、负序分量转换为直流量，分别采用PI控制器进行控制，使正、负序电流谐波均可被补偿。基于该方法，即使在断相容错时，k次电流谐波仍可被完全补偿。需注意，某些电机中，如单中性点六相电机，存在一额外零序子空间，该子空间中电流谐波一般用比例谐振控制器补偿，如图4点画线方框内所示。与图1所示传统谐波电流补偿方法相比，所提方法主要有两方面区别。首先，针对低频奇数k次谐波，所提方法在所有子空间都进行了补偿，而传统方法仅在αβk子空间进行补偿；其次，所提方法同时补偿各子空间内正、负序谐波，而图1a所示传统方法仅补偿正序谐波。以上两点区别是与表1所示的正常情况、断相情况下谐波电流子空间映射特性的差别相对应的。
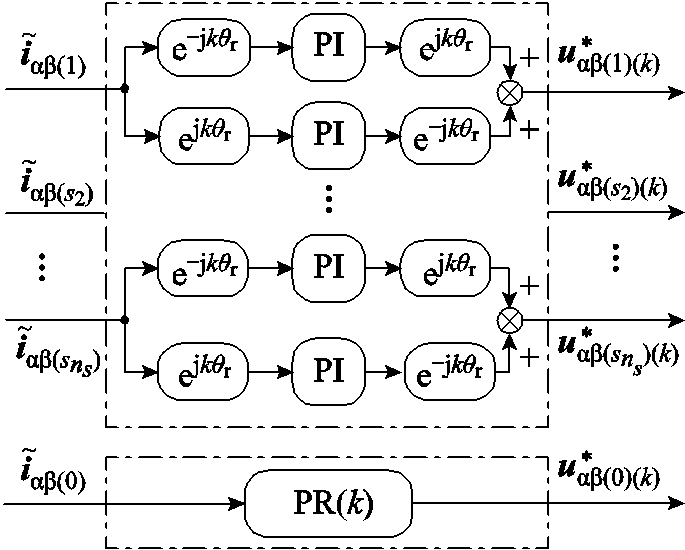
图4 适用于断相工况的改进k次谐波补偿方法
Fig.4 Improved k-th current harmonic compensation scheme in open-phase conditions
含基波电流容错控制和谐波电流补偿的电流控制器整体框图如图5所示。控制框图中，首先用式（24）将定子电流变换到各子空间，计算实际定子电流和参考值间的误差。有多个不同次数的电流谐波要补偿时，需要将多个图4所示结构并联。将定子电流误差传递到并联的控制器中，计算相应的控制电压。在并联的控制器的输出端，将各子空间中各次谐波电流的控制电压叠加起来，得到各子空间中最终参考电压，通过反变换转换为定子相电压参考值，利用PWM技术驱动逆变器在电机端口输出这些电压。
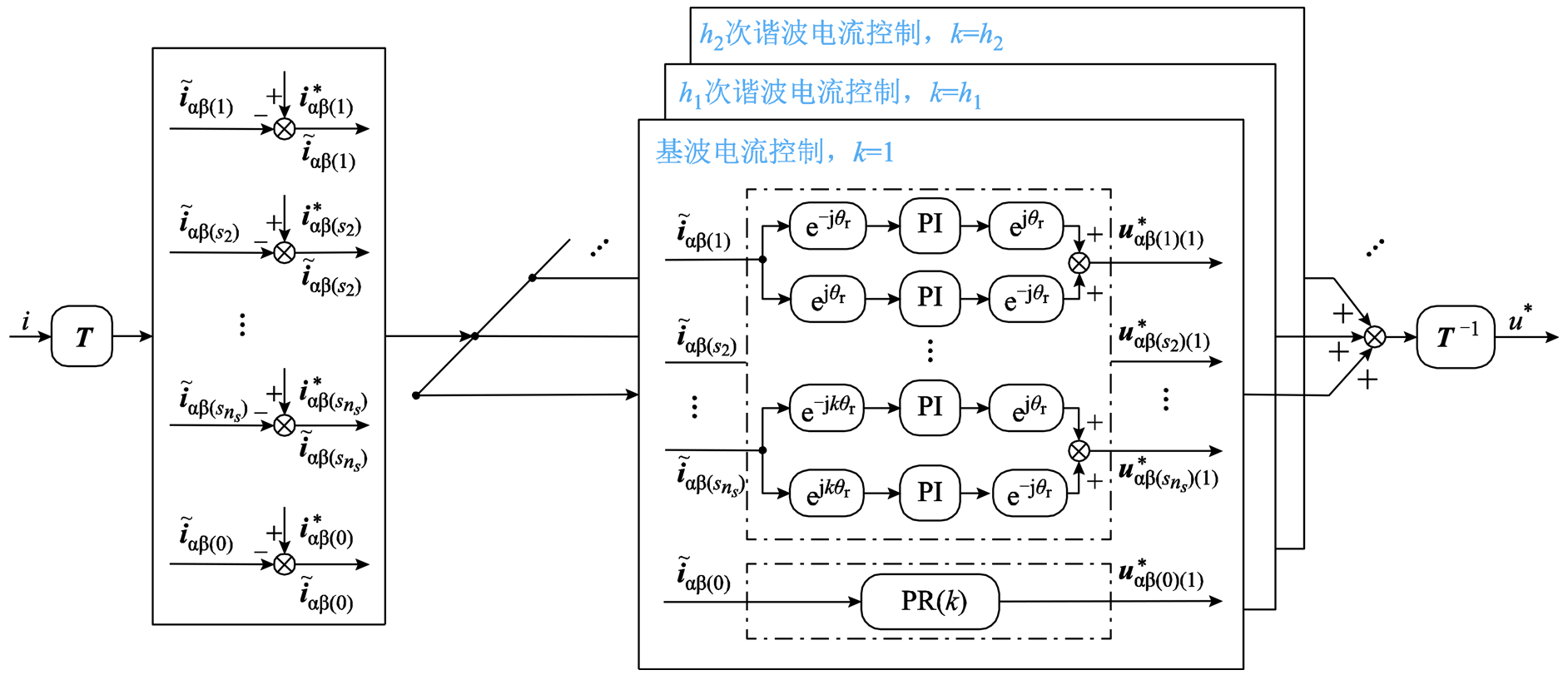
图5 同时考虑容错控制与谐波补偿时的整体电流控制框图
Fig.5 The whole current control scheme with both fault-tolerant control and harmonics compensation control
实验中使用的是一台对称型九相单中性点异步电机，其参数见表2。一台磁粉制动器与电机同轴相连作为负载。用一台九相VSI为电机供电。整个实验平台的照片如图6所示[24]。直流母线电压为400V，死区时间为5ms，控制器采用TITMS320F28335，控制频率为4kHz。开路故障通过断开逆变器与电机间断路器模拟。定子电流用一台录波仪进行测量。
图6 实验平台的照片[24]
Fig.6 Photograph of the experiment platform[24]
表2 九相异步电机参数
Tab.2 The parameters of the nine-phase machine
参数数值 定子电阻Rs/Ω1.13 转子电阻Rr/Ω0.432 极对数p2 额定电流IN/A5 定子漏感Lls/mH5 转子漏感Llr/mH12 αβ1中励磁电感Lm1/mH167 额定相电压UN/V225
断相容错运行时，定子电流参考值由最大转矩优化策略确定，因此容错运行时各正常相基波电流幅值基本相等[2]。计算定子电流参考值所需参数由离线优化获得并存储于控制器中。因控制器计算资源有限，实验中选择3、5、7次谐波电流进行补偿。这三种谐波幅值较大，对它们进行补偿可在计算资源有限的条件下获得较好的补偿效果。
首先对断相后谐波电流特性进行验证，在仅进行容错控制而不加入谐波补偿算法时，各次谐波电流在各子空间内分布情况如图7所示。用OPF(n1, n2, ×××, nc)表示当第n1, n2, ×××, nc相断相时的故障。图7的两种工况分别为正常工况和OPF(1)工况。图中给出了各子空间下各次电流谐波正负序分量的幅值。如图7a，正常工况下，3次谐波电流几乎完全为αβ3中的正序分量，幅值为2.40A。其他3次谐波分量幅值均小于0.105A，可忽略。5、7次谐波电流也有类似分布特性。
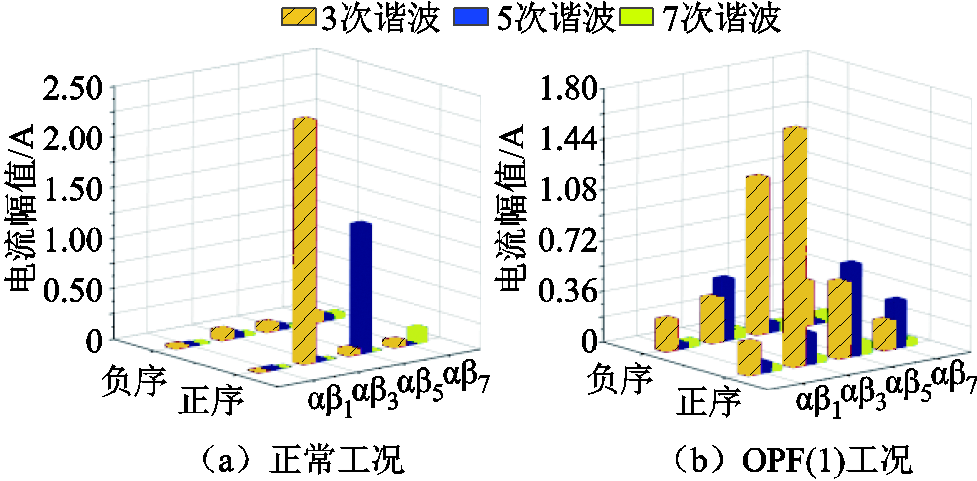
图7 无谐波补偿时两种不同工况下谐波电流映射情况
Fig.7 Current harmonics mapping in two different faulty conditions without harmonic compensation
然而，在图7b中的OPF(1)工况下，各次电流谐波不再集中于单一子空间内，而是分散在所有子空间中。以3次谐波为例，尽管αβ3中正序分量有最大的幅值（1.68A），但其他各分量也有较大幅值，如αβ5中负序分量幅值高达1.11A，除αβ3中正序分量以外的其他分量是不可忽略的。在OPF(1)工况下，5、7次谐波也有着类似的分布特性。
图7所示实验结果与理论推导中所得出的结论（见表1）一致，即正常运行时某次谐波电流只会以特定序分量的形式被映射到某一特定子空间当中，但断相故障下各次谐波电流将会同时被映射到所有子空间中，且各子空间中会同时出现各次谐波电流的正负序分量。
在正常工况、OPF(1)、OPF(1,3)、OPF(1,2,3)和OPF(1,2,3,5)共五种工况下比较了改进谐波补偿算法与图1a所示传统方法的性能。实验中，除谐波补偿算法外，其他实验条件不变。
OPF(1,2,3)工况下，两种谐波补偿算法定子电流波形比较如图8所示。整体电流波形如图8a所示，控制模式首先由无谐波补偿切换到传统谐波补偿方法，最后切换到改进谐波补偿方法。如图8b，不进行谐波补偿时，相电流有很大峰值和严重畸变。采用传统补偿方法时，如图8c，相电流峰值有所下降，谐波畸变改善，但仍含有较多3、5、7次谐波。采用改进谐波电流补偿方法时，相电流峰值进一步下降，谐波畸变得到明显抑制，3、5、7次谐波电流几乎被完全补偿，此时电流波形的畸变由更高次谐波造成。
图8 实验中OPF(1,2,3)工况下定子电流波形
Fig.8 Stator current waveforms in OPF(1,2,3) condition
为阐明断相容错时两种方法性能产生较大差异的原因，图9展示了OPF(1,2,3)工况下两种方法下电流谐波映射结果。图9a展示了传统方法下电流谐波在子空间中的映射情况。除传统方法加以补偿的分量（αβ3中的正序3次谐波，αβ5中的正序5次谐波，αβ7中的正序7次谐波），还有大量其他正、负序谐波分量分布于各子空间中。采用改进方法的结果如图9b所示，各子空间中3次、5次和7次谐波电流都几乎被完全补偿，证明了改进方法在断相容错时下优异的性能。
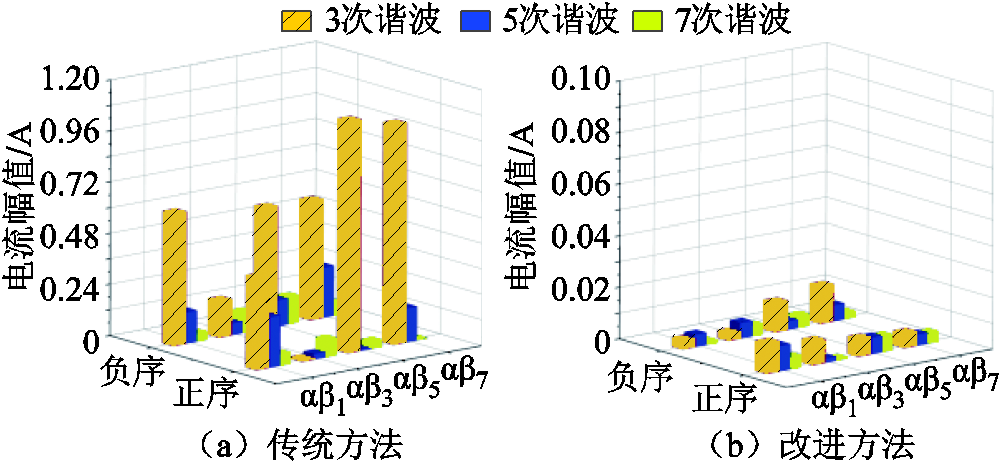
图9 OPF(1,2,3)工况，两种不同谐波补偿方法下谐波电流子空间映射情况
Fig.9 Current harmonics mapping in OPF(1,2,3) condition with two harmonic compensation methods
在图9a中，αβ1中有较大谐波分量。由于αβ1中励磁电感较大，其中的电流谐波会造成较大转矩脉动。采用改进算法时，αβ1中3、5、7次谐波电流得到补偿，电流谐波造成的转矩脉动会被大幅抑制。这一结果可更直观地从图10中的αβ1定子电流矢量轨迹得到。OPF(1,2,3)工况，两种不同谐波补偿方法下αβ1中定子电流空间矢量轨迹越接近圆形，定子基波磁动势越稳定，输出转矩越平稳。轨迹若偏离圆形，说明定子基波磁动势存在波动，输出转矩中存在脉动。如图10a，采用传统方法时，因低次电流谐波的存在，定子电流矢量轨迹明显偏离圆形参考值，会产生较大转矩脉动。采用改进方法时，如图10b，定子电流矢量轨迹几乎与参考圆重合，转矩脉动得到最大程度的抑制，系统容错控制性能得到了提升。
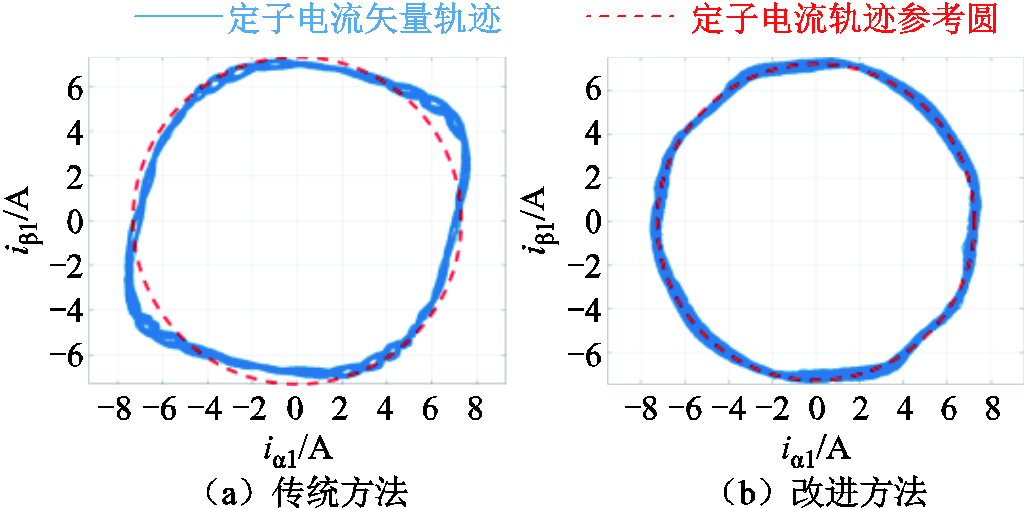
图10 OPF(1,2,3)工况，两种不同谐波补偿方法下αβ1中定子电流空间矢量轨迹
Fig.10 Current space vector trajectory in αβ1 in OPF(1,2,3)condition with two harmonics compensation methods.
为对谐波补偿效果进行总体评估，定义了k次电流谐波的含量Hk。
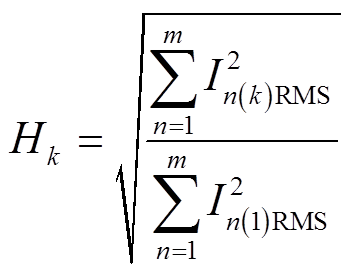（25）
式中，In(k)RMS为第n相中k次谐波电流有效值；In(1)RMS为第n相中基波电流有效值。五种工况下，各次电流谐波Hk值结果如图11所示。
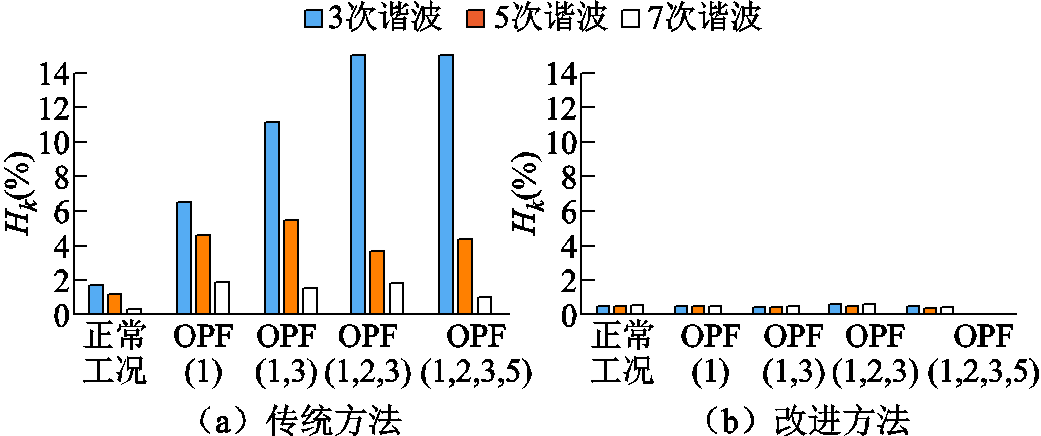
图11 五种故障工况下3、5、7次谐波电流含量情况
Fig.11 Harmonic contents of 3rd, 5th and 7th current harmonics in five faulty conditions
正常工况下，传统方法有较好性能。3、5、7次谐波电流含量分别为1.70%、1.13%和0.30%。采用改进方法后，正常工况3、5、7次谐波电流含量进一步下降为0.365%，0.382%和0.494%。正常工况下两种方法性能的差异主要是由相参数不一致等因素带来的细微不对称性造成的。与断相故障类似，不对称性会使谐波分布与式（3）相比产生细微偏离，生成无法由传统方法补偿的分量。而改进方法可补偿这些额外分量，在正常工况也有更好的性能。
故障工况下，传统方法效果严重恶化。单相断相时，各次谐波电流含量上升至6.55%、4.66%和1.86%。OPF(1,2,3,5)工况下，谐波电流含量进一步上升至15.72%、4.34%和0.98%。而改进方法在各容错工况下都有良好补偿效果，谐波电流含量在0.6%以下。
定子绕组损耗无法直接测量，在式（26）中定义了定子相电流总谐波畸变率（Total Harmonic Distortion, THD），以此作为定子绕组谐波损耗的量化指标。
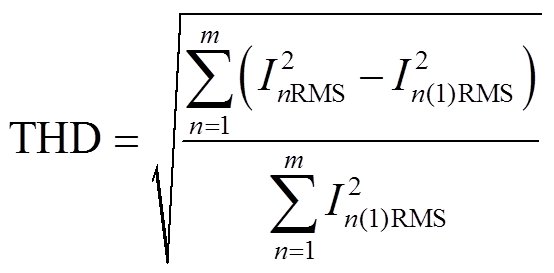（26）
式中，InRMS为第n相电流有效值。计算中仅考虑定子绕组铜损耗，且认为定子绕组电阻不随电流频率变化。实验中THD和根据THD计算的定子绕组谐波损耗见表3。表3中谐波损耗是用定子基波电流绕组损耗进行归一化后的结果。
表3 THD值和计算得到的定子绕组谐波损耗
Tab.3 THD values and calculated harmonic winding losses
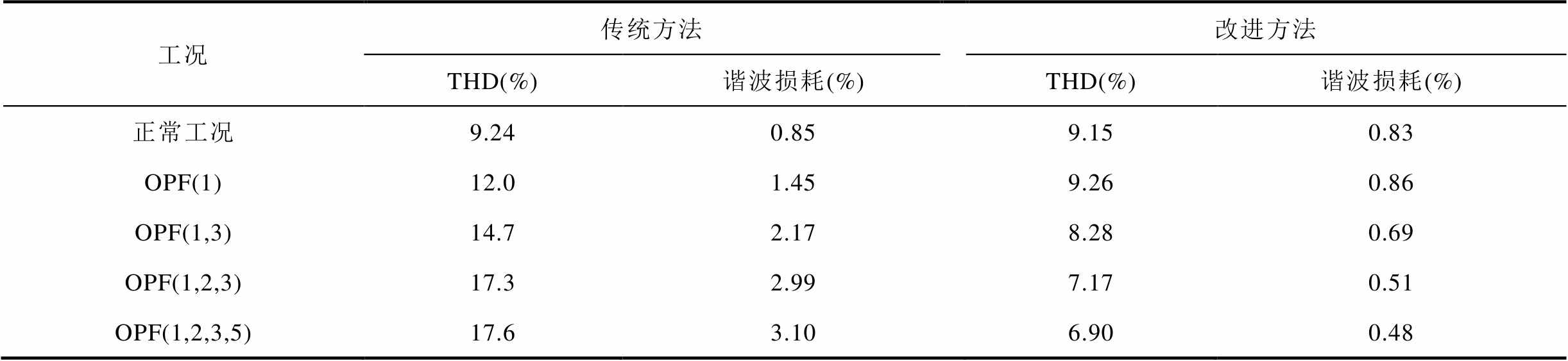
工况传统方法改进方法 THD(%)谐波损耗(%)THD(%)谐波损耗(%) 正常工况9.240.859.150.83 OPF(1)12.01.459.260.86 OPF(1,3)14.72.178.280.69 OPF(1,2,3)17.32.997.170.51 OPF(1,2,3,5)17.63.106.900.48
由表3可知，正常工况下，与传统方法相比，改进方法谐波电流补偿性能的提升可忽略。而在断相容错时，改进方法可显著降低电流THD和谐波损耗。OPF(1)工况下，改进方法可将THD从12.0%降到9.26%，定子绕组谐波损耗降低40.69%，定子绕组总损耗下降0.58%。随着断相数量增加，改进方法的优势进一步扩大。OPF(1,2,3,5)工况下，THD从17.6%下降到6.90%，定子绕组谐波损耗下降84.5%，定子绕组总损耗下降2.54%。表3结果中假设各次谐波电流下定子绕组有相同的电阻，但实际上，受趋肤效应等影响，电流频率上升时，等效电阻会增大[25]。此外，电流谐波也会在转子中产生额外铜耗，在定转子铁心中产生额外铁耗[26]。表3中统计的谐波损耗未包含趋肤效应等带来的额外定子铜耗、谐波电流带来的额外转子铜耗和定转子铁耗，因此，改进方法的降损效果会比表3中结果更加显著。
理论研究发现，断相容错时，各次谐波电流正负序分量将存在于所有子空间当中，这与正常情况下谐波电流子空间分布有很大差别，针对正常工况设计的传统谐波电流补偿算法在断相容错时性能会有较大恶化。为改善断相容错时谐波补偿性能，基于广义对称分量法，本文提出了一种改进谐波电流补偿算法。该算法可对各子空间内正、负序谐波电流分量进行补偿，在断相容错时也有良好的补偿性能。在一台九相异步电机上的实验表明，断相时，传统方法中某次谐波电流有效值可达到基波电流有效值的15%，而改进方法下这一数值下降至不到0.6%，证明了改进算法良好的性能。改进算法可在容错工况下降低电机损耗和转矩脉动，提升容错控制性能。
参考文献
[1] Levi E. Multiphase electric machines for variable-speed applications[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 1893-1909.
[2] Duran M J, Barrero F. Recent advances in the design, modeling, and control of multiphase machines—part II[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 459-468.
[3] 田代宗, 孙宇光, 王善铭, 等. 多相整流永磁同步发电机绕组内部相间短路的故障分析[J]. 电工技术学报, 2020, 35(6): 1262-1271.
Tian Daizong, Sun Yuguang, Wang Shanming, et al. Analysis of stator internal phase-to-phase short-circuit in the multiphase permanent magnet synchronous generator with rectifier load system[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1262-1271.
[4] 林晓刚, 黄文新, 姜文, 等. 共母线开绕组永磁同步电机缺相容错型直接转矩控制[J]. 电工技术学报, 2020, 35(24): 5064-5074.
Lin Xiaogang, Huang Wenxin, Jiang Wen, et al. Fault-tolerant direct torque control for open-end winding permanent magnet synchronous motor with common DC bus under open phase circuit[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5064-5074.
[5] 彭忠, 郑泽东, 刘自程, 等. 基于虚拟绕组和全阶观测器的五相感应电机无速度传感器容错控制策略[J]. 电工技术学报, 2018, 33(21): 4949-4961.
Peng Zhong, Zheng Zedong, Liu Zicheng, et al. A novel sensorless fault-tolerant control of five-phase induction machine using virtual winding and full-order observer[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4949-4961.
[6] Baneira F, Doval-Gandoy J, Yepes A G, et al. Control strategy for multiphase drives with minimum losses in the full torque operation range under single open-phase fault[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6275-6285.
[7] Liang Zhe, Liang Deliang, Kou Peng, et al. Postfault control and harmonic current suppression for a symmetrical dual three-phase SPMSM drive under single-phase open-circuit fault[J]. IEEE Access, 8: 67674-67686.
[8] Huang Wentao, Hua Wei, Chen Fuyang, et al. Enhanced model predictive torque control of fault-tolerant five-phase permanent magnet synchronous motor with harmonic restraint and voltage preselection[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6259-6269.
[9] Yepes A G, Malvar J, Vidal A, et al. Current harmonics compensation based on multiresonant control in synchronous frames for symmetrical-phase machines[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2708-2720.
[10] 孟繁庆, 易新强, 刘海涛, 等. 三次谐波注入下多相感应电机稳态性能分析[J]. 电工技术学报, 2020, 35(16): 3396-3405.
Meng Fanqing, Yi Xinqiang, Liu Haitao, et al. Steady-state performance analysis of multiphase induction motor with third-order harmonic injection[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3396-3405.
[11] 肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615.
Xiao Yang, Song Jinyuan, Qu Renhao, et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2607-2615.
[12] Geng Yiwen, Lai Zou, Li Yonggang, et al. Sensorless fault-tolerant control strategy of six-phase induction machine based on harmonic suppression and sliding mode observer[J]. IEEE Access, 7: 110086-110102.
[13] Huang Qiuliang, Chen Yong, Xu Li. Fault-tolerant control strategy for five-phase PMSM with third-harmonic current injection[J]. IEEE Access, 6: 58501-58509.
[14] Liu Guohai, Lin Zhipeng, Zhao Wenxiang, et al. Third harmonic current injection in fault-tolerant five-phase permanent-magnet motor drive[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6970-6979.
[15] Arafat A K M, Choi S. Active Current harmonic suppression for torque ripple minimization at open-phase faults in a five-phase PMa-SynRM[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 922-931.
[16] Liu Zicheng, Zheng Zedong, Xu Lie, et al. Current balance control for symmetrical multiphase inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4005-4012.
[17] Etxeberria-Otadui I, Lopez De Heredia A, Gaztanaga H, et al. A single synchronous frame hybrid (SSFH) multifrequency controller for power active filters[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1640-1648.
[18] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021(8): 1671-1680.
Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead-time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Electrotechnical Society, 2021(8): 1671-1680.
[19] 倪瑞政, 李庭, 陈杰, 等. 一种脉冲式死区补偿方法的研究[J]. 电工技术学报, 2019, 34(增刊2): 553-559.
Ni Ruizheng, Li Ting, Chen Jie, et al. Research on a pulse dead zone compensation method[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 553-559.
[20] Shen Zewei, Jiang Dong. Dead-time effect compensation method based on current ripple prediction for voltage-source inverters[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 971-983.
[21] Grandi G, Loncarski J. Analysis of dead-time effects in multi-phase voltage source inverters[C]//6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, 2012: 1-6.
[22] Fortescue C L. Method of symmetrical co-ordinates applied to the solution of polyphase networks[J]. Transactions of the American Institute of Electrical Engineers, 1918, XXXVII(2): 1027-1140.
[23] 缪惠宇, 梅飞, 张宸宇, 等. 基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J]. 电工技术学报, 2019, 34(17): 3622-3630.
Miao Huiyu, Mei Fei, Zhang Chenyu, et al. Three phase unbalanced control strategy for virtual synchronous rectifier based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3622-3630.
[24] Sun Jiawei, Liu Zicheng, Zheng Zedong, et al. An online global fault-tolerant control strategy for symmetrical multiphase machines with minimum losses in full torque production range[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2819-2830.
[25] Stoyanov L, Lazarov V, Zarkov Z, et al. Influence of skin effect on stator windings resistance of AC machines for electric drives[C]//2019 16th Conference on Electrical Machines, Drives and Power Systems (ELMA), Varna, Bulgaria, 2019, : 1-6.
[26] Debruyne C, Desmet J, Derammelaere S, et al. Derating factors for direct online induction machines when supplied with voltage harmonics: a critical view[C]//2011 IEEE International Electric Machines & Drives Conference, Niagara Falls, ON, Canada, 2011: 1048-1052.
Analysis and Compensation of Current Harmonics in Symmetrical Multiphase Machines in Fault-Tolerant Operation against Open-Phase Faults
Abstract Multiphase machines have the advantages of high reliability, high fault-tolerant ability and high control flexibility. This paper studies the characteristics and compensation of low order current harmonics in multiphase machines during open-phase fault-tolerant operation. For a specific order current harmonic, positive and negative sequence components exist at the same time in all the subspaces in open-phase fault-tolerant operation. Traditional current harmonic compensation methods only compensate the selected order current harmonic in a specific subspace, therefore have seriously degraded performance in fault-tolerant operation. This paper proposes an improved current harmonic compensation method. With the Generalized Symmetrical Components Transformation and double PI controllers, positive and negative sequence current harmonics can be compensated in all the subspaces, which guarantees the good compensation performance in fault-tolerant operation. Finally, experiments were done on a nine-phase induction machine to verify the effectiveness of the proposed method and experimental results show the selected current harmonics can be completely compensated. Additional losses and torque ripple caused by current harmonics are reduced.
keywords：Multiphase machines, open-phase faults, fault-tolerant control, current control, harmonic compensation
DOI:10.19595/j.cnki.1000-6753.tces.211256
中图分类号：TM301.2
国家自然科学基金山东联合基金资助（项目名称：大容量高性能多相永磁直驱电力推进系统关键科学问题研究项目编号：U2016217）。
收稿日期 2021-08-11
改稿日期 2021-09-20
孙嘉伟 男，1994年生，博士研究生，研究方向为多相感应电机高性能控制。E-mail：thu_sjw@126.com
郑泽东男，1980年生，副教授，博士生导师，研究方向为电力电子与电气传动。E-mail：zzd@mail.tsinghua.edu.cn（通信作者）
（编辑 郭丽军）