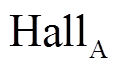 、
、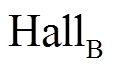 和
和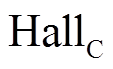 ),其安装位置以三相绕组的磁动势轴线为基准呈中心对称。其输出信号
),其安装位置以三相绕组的磁动势轴线为基准呈中心对称。其输出信号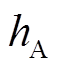 、
、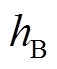 和
和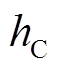 为三相相位差为
为三相相位差为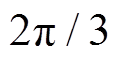 、周期为
、周期为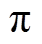 电角度的方波。
电角度的方波。摘要 在电动助力车用永磁同步电机(PMSM)控制系统中,针对PMSM在正常运行过程中发生霍尔位置传感器安装位置偏移的问题,提出基于带通频率跟踪滤波器的电机转子位置与速度估算方法。该算法将三相霍尔信号通过坐标变换转换为霍尔矢量,通过带通频率跟踪滤波器与锁相环提取霍尔矢量中的电机转子位置信息,以实现在霍尔位置传感器安装位置偏移情况下,对永磁同步电机转子位置与速度信息的正确估算。通过实验验证,该算法有效地减小了在霍尔位置传感器发生安装位置偏移时电机转速与电流的波动,提高了控制系统的可靠性和稳定性。
关键词:电动助力车 永磁同步电机 霍尔位置传感器 安装位置偏移 带通频率跟踪滤波器
随着电动助力车的发展,其作为一种便捷、环保的交通工具在国内外有着广大的市场前景[1-2]。电动助力车用驱动电机作为车辆的核心动力单元,与整车的性能有着密不可分的关系[3-4]。随着永磁材料的发展,永磁同步电机(Permanent Magnet Syn-chronous Motor, PMSM)逐渐走向小体积与低成本化,又凭借其能效比高、易于控制等优点[5-7],逐步成为电动助力车用驱动电机的首选。在控制算法中获取永磁同步电机的转子位置信息和速度信息方面,采用高精度位置传感器可保障电机有较好的控制效果,如旋转变压器与光电编码器等位置传感器可对转子位置进行实时高精度的跟踪,对于电机转速控制、输出峰值电流抑制与噪声抑制等方面有较好的有效性。但在电动助力车行业中,使用高精度位置传感器无疑会使研发与生产成本增加,且在各类使用场景中,生产厂商也多采用中低速PMSM作为电动助力车的驱动电机,采用高精度传感器也造成了不必要的资源浪费。而低分辨率位置传感器,如开关型霍尔位置传感器凭借其价格低廉、响应迅速、可满足矢量控制要求等优点,常被应用于电动助力车的永磁同步电机矢量控制中[8-14]。但是在日常使用中,安装于电机转子轴末端或轮毂内侧的霍尔位置传感器,在大批量组装阶段,难免会产生较大的公差,导致永磁同步电机的矢量控制系统无法正常工作,影响车辆驱动电机的稳定性[15-16],危害行车安全。
针对霍尔位置传感器安装偏移误差造成无法准确获取转子位置与转速信息等问题,文献[17]提出了一种新的组合换向优化策略,以获得理想的换向位置。新策略包括两个过程:平均失调的霍尔信号和补偿平均的霍尔信号。建立了直流母线电流与总偏差误差之间的数学关系,并建立了比例积分控制器来补偿换向位置。该组合优化方法有效地保障了在霍尔位置传感器安装偏移误差下电机的正常运行。但该组合优化方法需要滤除由于负载或速度波动引起的电流噪声,这限制了此方法在负载或速度大范围波动中的使用。文献[18]提出一种在极低速区域或速度过渡时期,利用速度和增量速度作为输入,通过模糊逻辑估计转子位置与转子转速的方法,该模糊逻辑估计的转子位置误差小于用平均霍尔间隔估计的转子位置误差,有效地解决了在电机低转速区间内转子位置的精确估算。但该算法在中高速转速区间内估算响应速度较慢,对控制器算力要求较高,难以在低成本的电动助力车领域中投入使用。文献[19]提出一种通过旋转矢量法减小低分辨率位置传感器输出误差的方法。旋转矢量形式的位置反馈采用空间矢量模型和解耦观测器拓扑,提高了观测器状态估计精度。空间旋转矢量法改善了低分辨率传感器位置估计,但由于量化干扰输入的不精确性质,估计仍然包含少量的误差。文献[20]提出一种结合低分辨率霍尔传感器输出信号的矢量跟踪位置观测器,类似于锁相环结构。该系统由基于定子模型单位反电动机矢量的位置误差检测器和比例积分型控制器组成,使位置误差快速收敛于零。文献[21]提出一种基于霍尔矢量频率跟踪的电机转子位置与速度估算方法,在三相开关型霍尔传感器安装不准确造成霍尔信号偏移的情况下,可以精确估计转子的速度和位置。首先,通过坐标变换得到与转子位置相关的霍尔向量;然后,利用同步频率跟踪滤波器从霍尔矢量的两个正交分量中提取位置信息的正弦基波和余弦基波;最后利用arctan函数解耦计算电机转子的速度和位置。但是,该方法采用的同步频率跟踪滤波器的通频带和品质因数与电机转速存在一定相关性,且采用arctan函数提取基波,不利于中低转速下的永磁同步电机转子位置与速度估算。
本文针对霍尔位置传感器安装位置偏移下的永磁同步电机的矢量控制,提出了一种基于带通频率跟踪滤波器的PMSM转子位置与速度估算方法,将三相霍尔信号通过坐标变换为霍尔矢量,通过带通频率跟踪滤波器与锁相环提取霍尔矢量中电机转子的位置与速度信息,实现永磁同步电机的补偿控制。使得补偿控制前后的转速与电流值能够满足电机正常运行的要求,减小了转速与电流的波动,提高了控制系统的稳定性。
霍尔位置传感器安装示意图如图1所示,以极对数为4的永磁同步电机为例,对于按120°分布式安装的三相开关型霍尔位置传感器(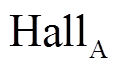 、
、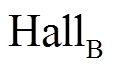 和
和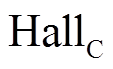 ),其安装位置以三相绕组的磁动势轴线为基准呈中心对称。其输出信号
),其安装位置以三相绕组的磁动势轴线为基准呈中心对称。其输出信号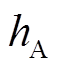 、
、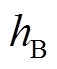 和
和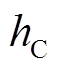 为三相相位差为
为三相相位差为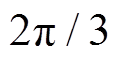 、周期为
、周期为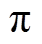 电角度的方波。
电角度的方波。
这些离散信号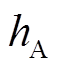 、
、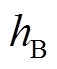 、
、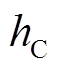 共有六种组合输出状态,在霍尔位置传感器无安装偏移误差的理想状态下,该六种组合输出状态将一个
共有六种组合输出状态,在霍尔位置传感器无安装偏移误差的理想状态下,该六种组合输出状态将一个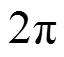 的电角度周期均分为六个
的电角度周期均分为六个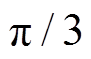 电角度的位置区间。霍尔信号组合状态值如图2所示,
电角度的位置区间。霍尔信号组合状态值如图2所示,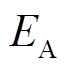 、
、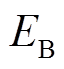 、
、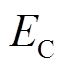 为三相反电动势,
为三相反电动势,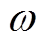 为电机转子的电角速度。为了简化后续分析,将此六种组合状态的表现形式转换为区间编码,即
为电机转子的电角速度。为了简化后续分析,将此六种组合状态的表现形式转换为区间编码,即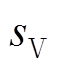 、
、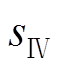 、
、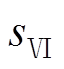 、
、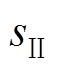 、
、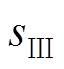 与
与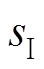 。
。
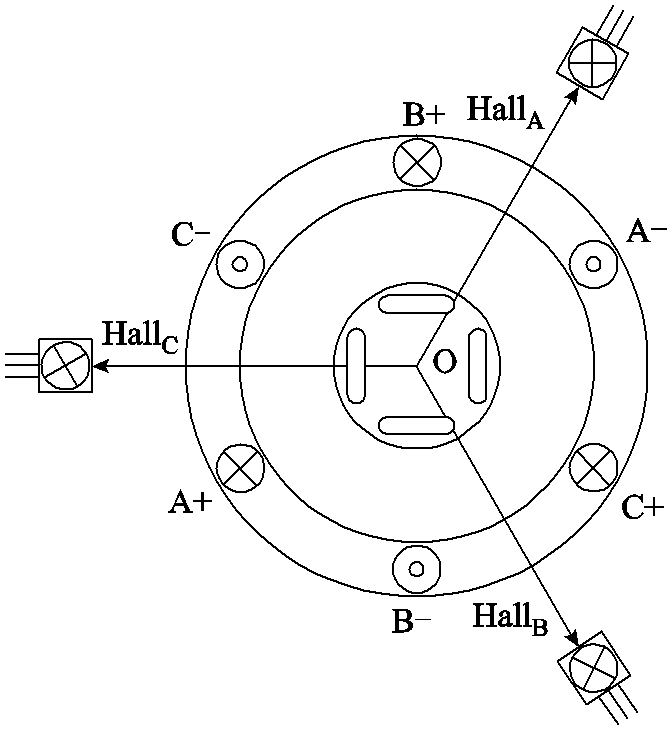
图1 霍尔位置传感器安装示意图
Fig.1 Hall position sensor installation schematic
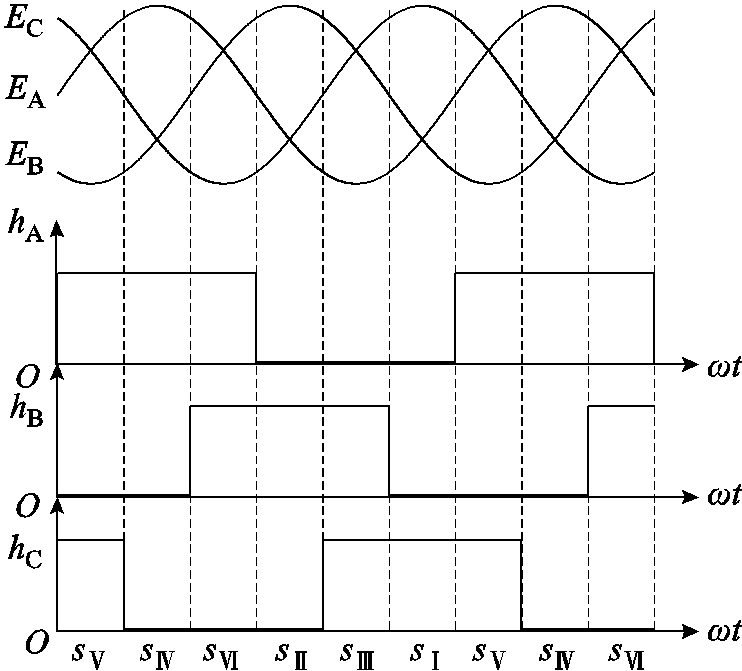
图2 霍尔信号组合状态值
Fig.2 Hall signal combination state value diagram
根据霍尔效应,当霍尔位置传感器安装位置超前偏移误差时,则超前输出转子磁场的切换状态,安装位置滞后偏移误差时则与之相反。假设电机转子按顺时针方向转动,超前偏移误差角度为正向误差,滞后偏移误差角度为负向误差。以图3为例,三相霍尔位置传感器的安装位置偏移的误差角度分别为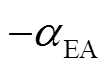 、
、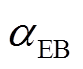 、
、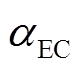 。
。
此时,存在上述霍尔位置传感器安装偏移误差角度的状态下,每个霍尔信号电角度的区间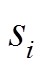 值不再为
值不再为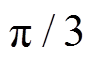 ,霍尔位置传感器安装偏移误差下的霍尔信号输出波形如图4所示。区间角度偏差情况可通过式(1)估算。
,霍尔位置传感器安装偏移误差下的霍尔信号输出波形如图4所示。区间角度偏差情况可通过式(1)估算。
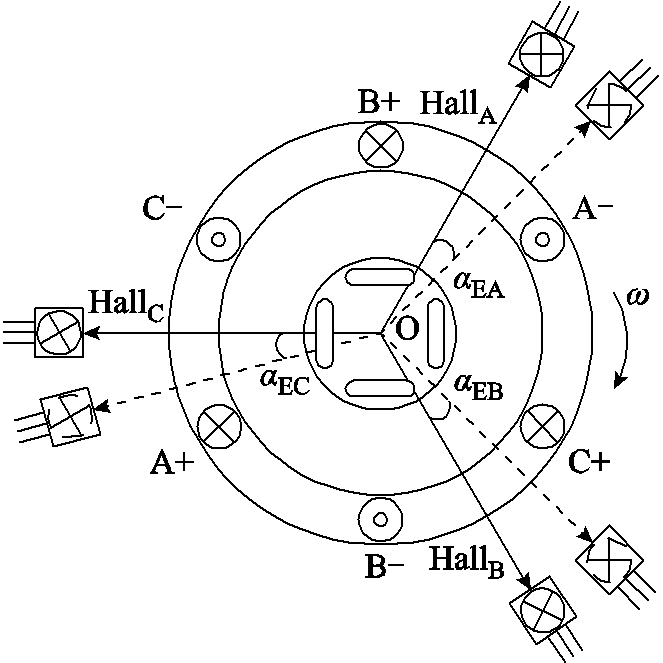
图3 霍尔位置传感器安装偏移误差示意图
Fig.3 Schematic diagram of the installation offset error of the Hall position sensor
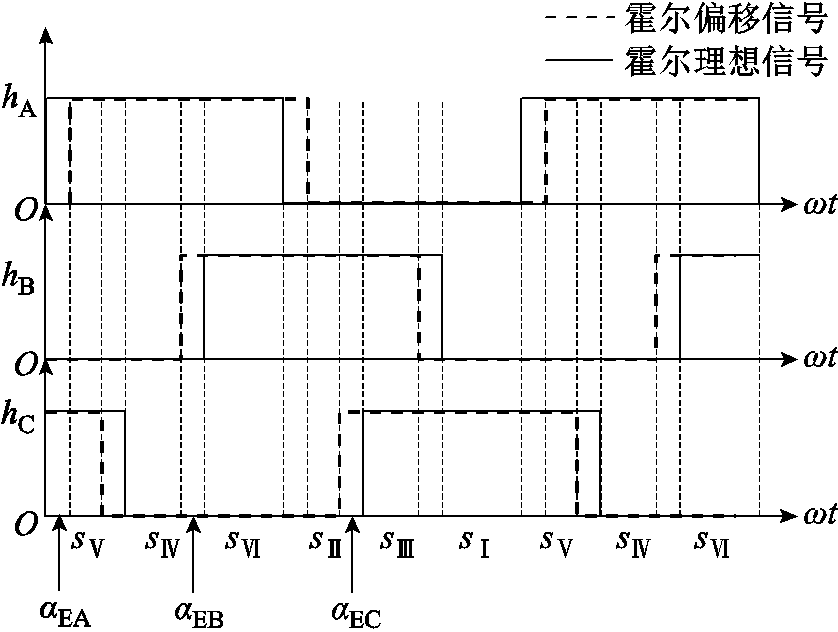
图4 霍尔位置传感器安装偏移误差下的霍尔信号输出波形
Fig.4 Hall signal output waveform under the installation offset error of the Hall position sensor
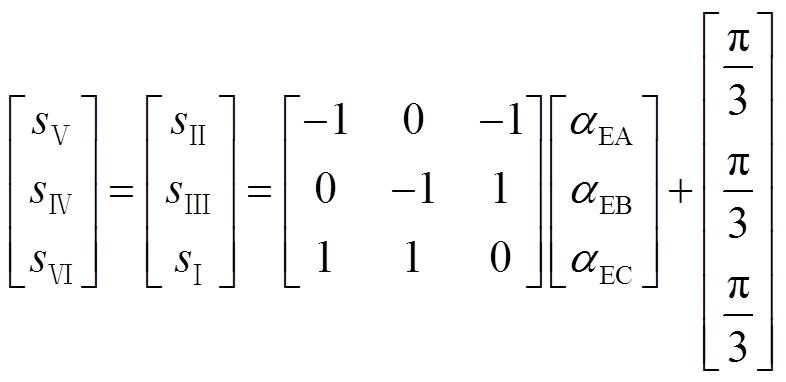 (1)
(1)
实际测速过程中,可利用霍尔位置传感器输出信号,通过传统T法进行电机转子位置与转速估计。当控制器MCU时钟以频率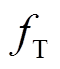 进行高频计数脉冲输出,若第
进行高频计数脉冲输出,若第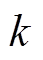 个电角度位置区间内共有
个电角度位置区间内共有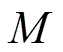 个计数时钟脉冲,则其脉冲间的时间间隔为
个计数时钟脉冲,则其脉冲间的时间间隔为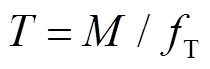 ,该区间内的电机转速可根据式(2)进行估算。
,该区间内的电机转速可根据式(2)进行估算。
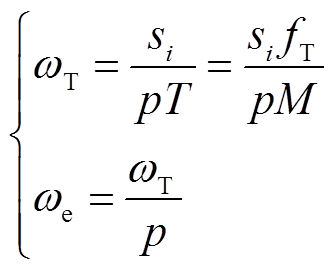 (2)
(2)
式中,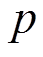 为电机的极对数;
为电机的极对数;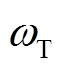 为电机的机械转速;
为电机的机械转速;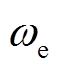 为电机转子的电角速度。
为电机转子的电角速度。
在估算电机转子位置时,可利用第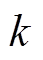 个电角度位置区间内T法测速得到的转子平均电角速度,通过式(3)进行第
个电角度位置区间内T法测速得到的转子平均电角速度,通过式(3)进行第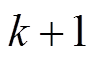 位置区间内的转子位置估算。
位置区间内的转子位置估算。
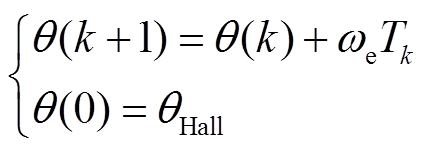 (3)
(3)
式中,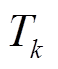 为第
为第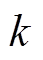 个电角度区间内的采样时间;
个电角度区间内的采样时间;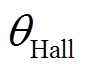 为霍尔位置传感器检测得的电机转子起始位置。
为霍尔位置传感器检测得的电机转子起始位置。
T法估算位置曲线与实际位置曲线对比如图5所示,当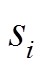 的电角度区间值不为
的电角度区间值不为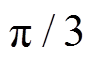 时,根据式(3)估算的转子转速信息与转子位置信息会出现不连续的状态,造成严重的估计误差,导致转子位置估算曲线的畸变,使得电机在正常控制算法下的运转过程中出现各类异常工况。
时,根据式(3)估算的转子转速信息与转子位置信息会出现不连续的状态,造成严重的估计误差,导致转子位置估算曲线的畸变,使得电机在正常控制算法下的运转过程中出现各类异常工况。
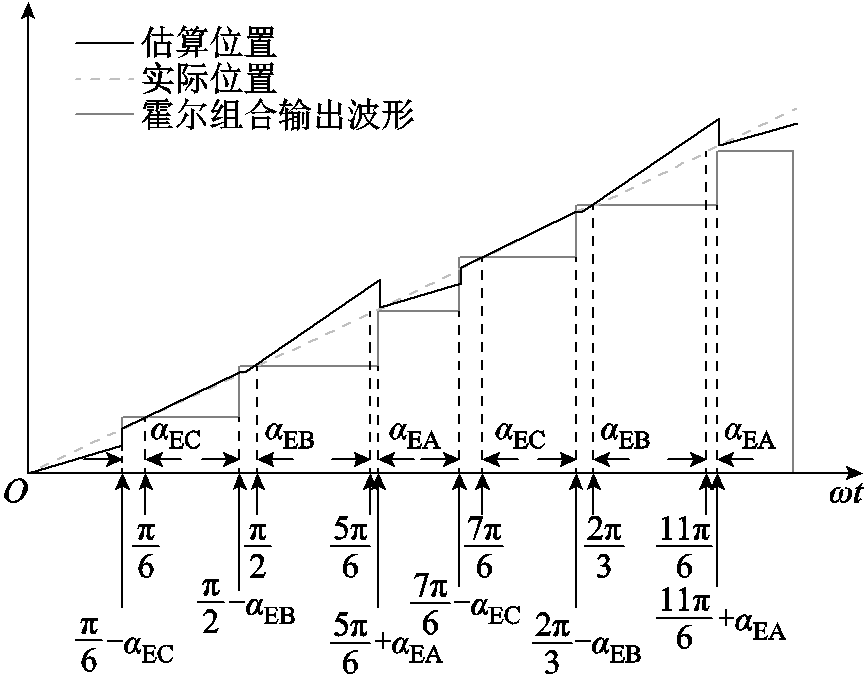
图5 T法估算位置曲线与实际位置曲线对比
Fig.5 Comparison of T-method estimated position curve and actual position curve
霍尔信号矢量变换将自然坐标系下的三相霍尔位置传感器输出信号经坐标变换至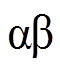 静止坐标系下,使得霍尔信号与转子位置间的关系更加清晰且便于分析。
静止坐标系下,使得霍尔信号与转子位置间的关系更加清晰且便于分析。
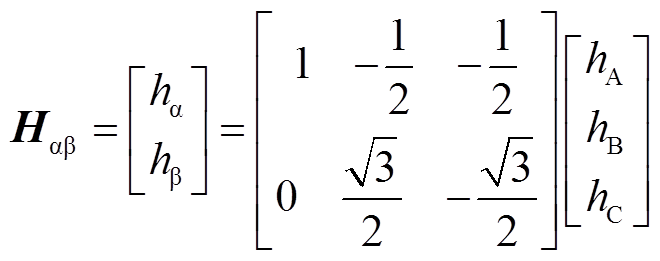 (4)
(4)
式(4)将三相霍尔信号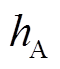 、
、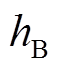 、
、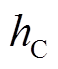 变换为一个霍尔矢量
变换为一个霍尔矢量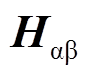 ,其中
,其中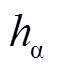 与
与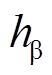 为
为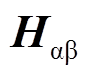 的一对正交分量。若将转子电角度位置
的一对正交分量。若将转子电角度位置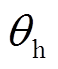 记为
记为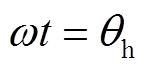 ,那么
,那么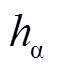 与
与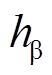 可记为以
可记为以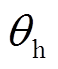 为相位的信号函数,且满足
为相位的信号函数,且满足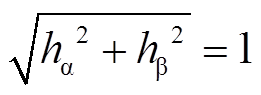 。
。
实际上,在电机正常运行时,转子位置是连续变化的角度值,因此可将离散的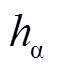 与
与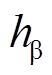 分别视为关于
分别视为关于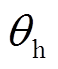 的余弦与正弦信号函数。霍尔矢量与转子电角度区间关系如图6所示,
的余弦与正弦信号函数。霍尔矢量与转子电角度区间关系如图6所示,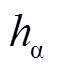 和
和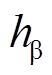 与转子电角度区间关系如图7所示,将霍尔矢量
与转子电角度区间关系如图7所示,将霍尔矢量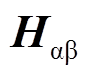 的相位
的相位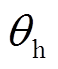 与电角度扇区
与电角度扇区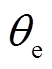 进行对比后可得三相霍尔信号与霍尔矢量间的关系见表1。
进行对比后可得三相霍尔信号与霍尔矢量间的关系见表1。
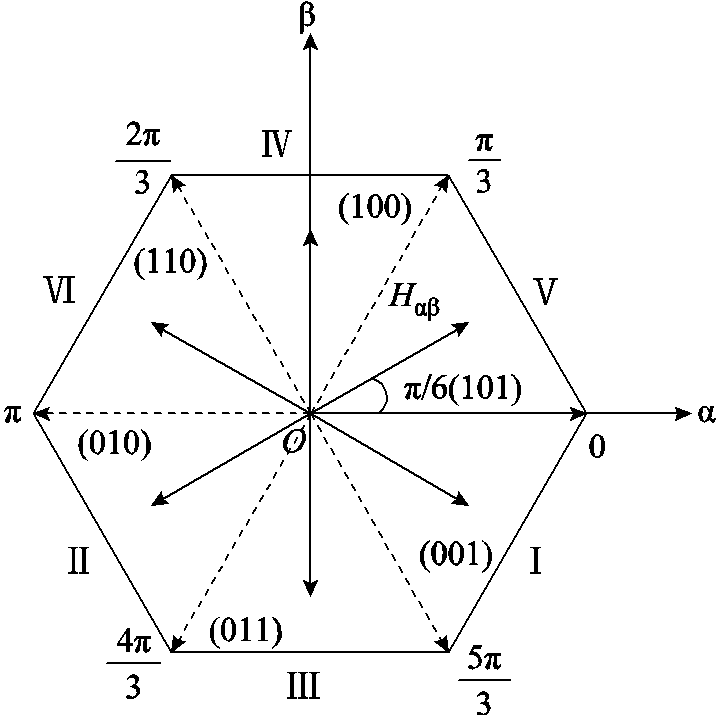
图6 霍尔矢量与转子电角度区间关系
Fig.6 Interval relationship between Hall vector and rotor electrical angle
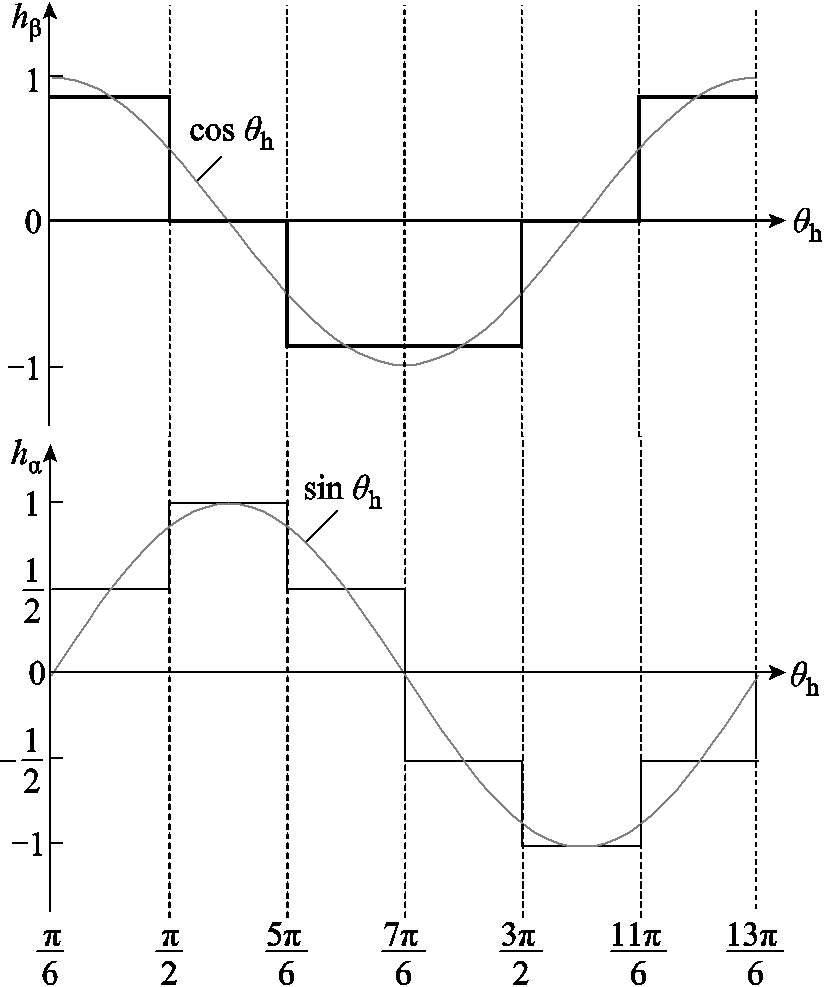
图7 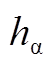 ,
,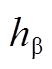 与转子电角度区间关系
与转子电角度区间关系
Fig.7 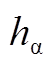 ,
,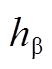 and interval relationship with rotor electric angle
and interval relationship with rotor electric angle
以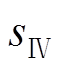 扇区为例,转子位置电角度
扇区为例,转子位置电角度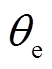 处于p/3~ 2p/3,图6中对应的霍尔矢量信号对应的相位值
处于p/3~ 2p/3,图6中对应的霍尔矢量信号对应的相位值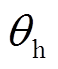 位于p/2~ 5p/6之间。同理可知其余五个区间霍尔矢量信号的相位值
位于p/2~ 5p/6之间。同理可知其余五个区间霍尔矢量信号的相位值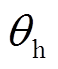 与转子位置电角度
与转子位置电角度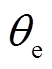 间的关系为
间的关系为
表1 霍尔矢量与转子电角度区间关系表
Tab.1 Hall vector and rotor electrical angle interval relation table

霍尔信号霍尔矢量
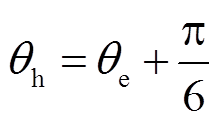 (5)
(5)
在正常工况下,电机以转速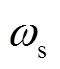 进行匀速运转时,霍尔矢量
进行匀速运转时,霍尔矢量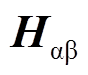 可通过快速傅里叶变换(Fast Fourier Transform, FFT)后表示为
可通过快速傅里叶变换(Fast Fourier Transform, FFT)后表示为
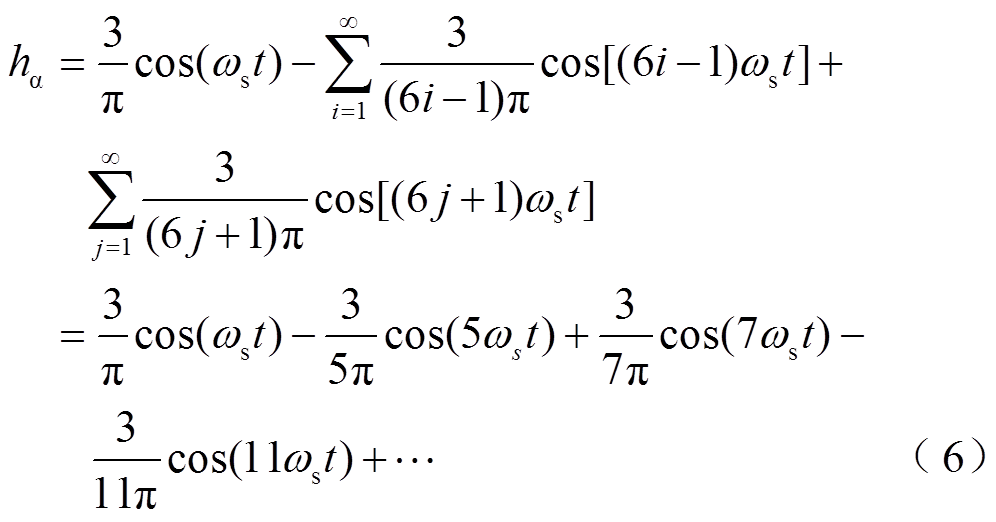
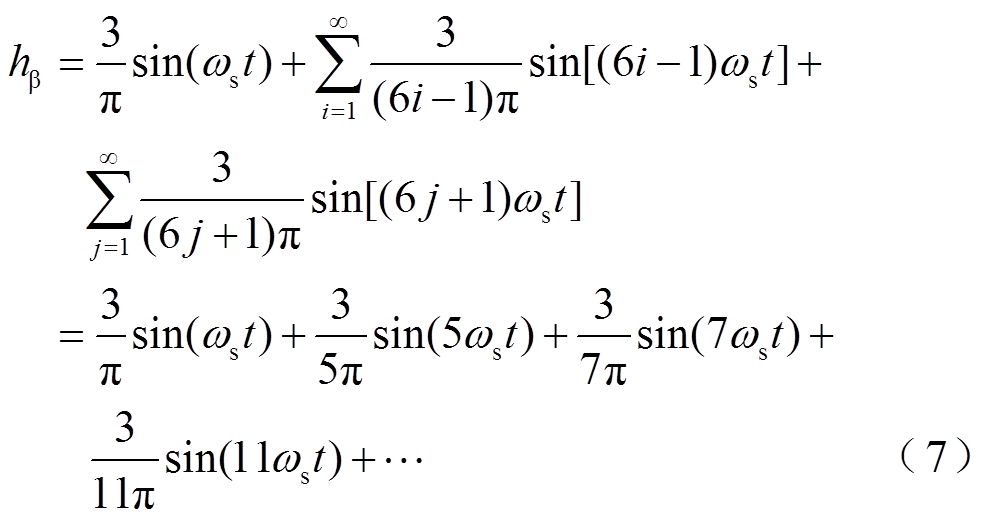
式中,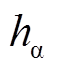 和
和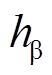 均含有基波分量与
均含有基波分量与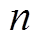
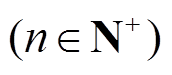 阶高次谐波分量。其中,
阶高次谐波分量。其中,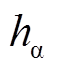 和
和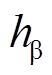 的基波分量分别是关于转子电角度速度
的基波分量分别是关于转子电角度速度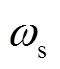 的余弦信号函数和正弦信号函数,高次谐波分量含有
的余弦信号函数和正弦信号函数,高次谐波分量含有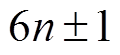 次谐波分量。因此,由式(6)与式(7)可知,可从基波分量中提取电机转子的转速与位置信息,而其余谐波分量则为高次谐波干扰。
次谐波分量。因此,由式(6)与式(7)可知,可从基波分量中提取电机转子的转速与位置信息,而其余谐波分量则为高次谐波干扰。
然而,在霍尔位置传感器安装位置偏移的情况下,霍尔信号的提前或滞后会导致霍尔矢量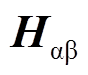 的两个正交分量出现波形畸变,在离散区间内产生失真,使得信号分量不再完全正交,
的两个正交分量出现波形畸变,在离散区间内产生失真,使得信号分量不再完全正交,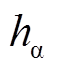 和
和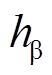 经FFT后输出的频谱也相应发生总谐波失真。
经FFT后输出的频谱也相应发生总谐波失真。
无偏移误差和偏移误差下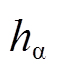 和
和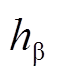 的谐波次序分别如图8和图9所示。通过对比图8与图9,当霍尔位置传感器存在安装偏移误差时,频谱中出现
的谐波次序分别如图8和图9所示。通过对比图8与图9,当霍尔位置传感器存在安装偏移误差时,频谱中出现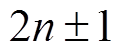 次谐波分量,而基波分量的幅值与无安装偏移误差的情况基本一致。又由于基波分量的相位值与转子电角度存在式(5)的相关性,因此可通过提取霍尔矢量的两个正交基波分量来获取转子的电角速度与电角度位置信息。
次谐波分量,而基波分量的幅值与无安装偏移误差的情况基本一致。又由于基波分量的相位值与转子电角度存在式(5)的相关性,因此可通过提取霍尔矢量的两个正交基波分量来获取转子的电角速度与电角度位置信息。
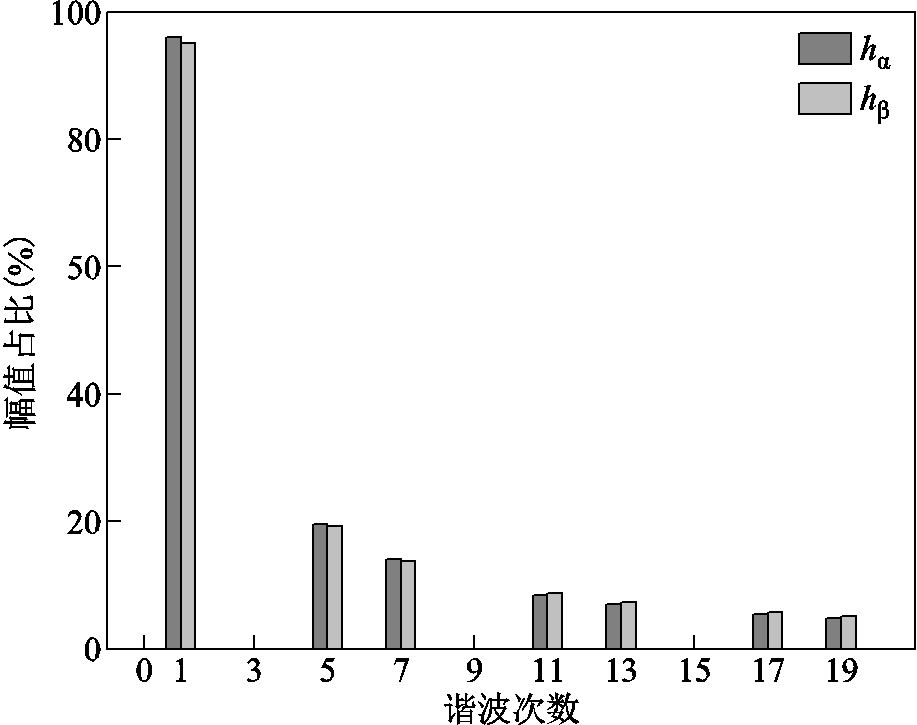
图8 无偏移误差下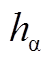 和
和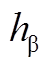 的谐波分量
的谐波分量
Fig.8 Harmonic order of 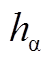 ,
,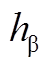 without offset error
without offset error
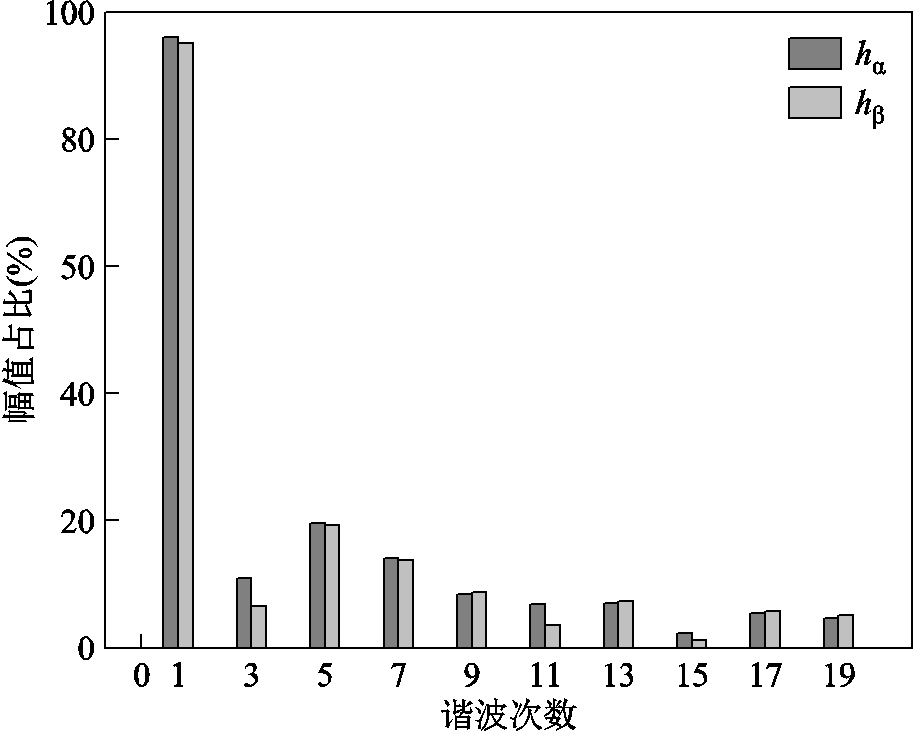
图9 偏移误差下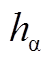 和
和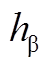 的谐波分量
的谐波分量
Fig.9 Harmonic order of 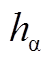 ,
,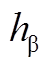 under offset error
under offset error
根据上述分析,在发生霍尔位置传感器安装偏移的情况下,霍尔矢量的两个正交基波分量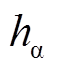 和
和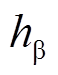 中均含有高次谐波分量,因此采用低通或带通滤波器对高次谐波分量进行滤除即可获得霍尔矢量的基波分量信号。然而,基波、谐波信号频率与电机电角速度
中均含有高次谐波分量,因此采用低通或带通滤波器对高次谐波分量进行滤除即可获得霍尔矢量的基波分量信号。然而,基波、谐波信号频率与电机电角速度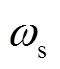 相关,随着电机的变加速度运动,信号频率
相关,随着电机的变加速度运动,信号频率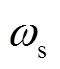 也随之改变,传统固定截止频率的低通或带通滤波器均无法满足滤除动态频率高次谐波分量的要求,因此,本文提出了一种新型的带通频率跟踪滤波器,结构框如图10所示。
也随之改变,传统固定截止频率的低通或带通滤波器均无法满足滤除动态频率高次谐波分量的要求,因此,本文提出了一种新型的带通频率跟踪滤波器,结构框如图10所示。
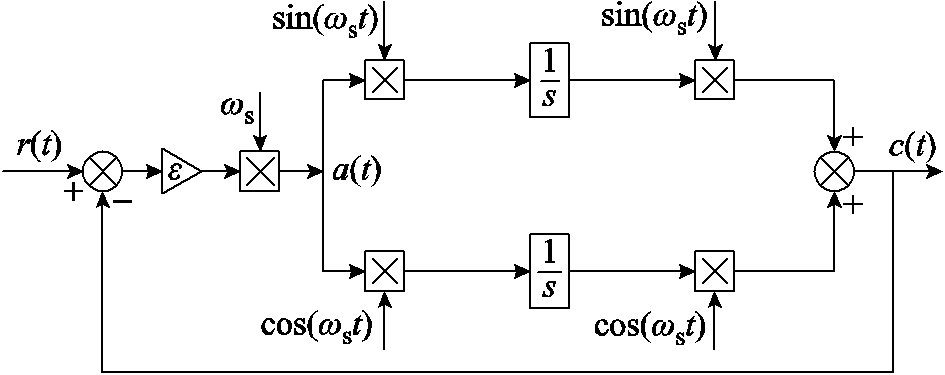
图10 带通频率跟踪滤波器结构框图
Fig.10 Block diagram of band-pass frequency tracking filter
图10中,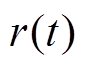 为输入信号,
为输入信号,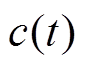 为滤波器输出,
为滤波器输出,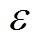 为滤波器增益系数。频率跟踪滤波器的输出为
为滤波器增益系数。频率跟踪滤波器的输出为
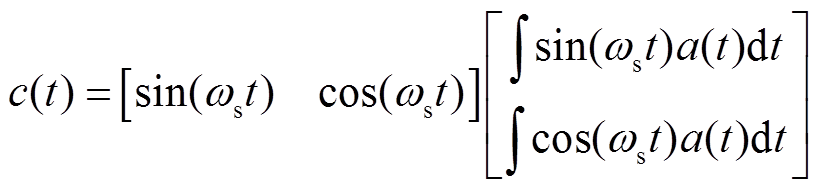 (8)
(8)
对式(7)求二阶微分得
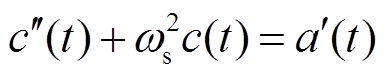 (9)
(9)
于是,由输出信号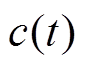 与
与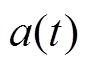 所确定的传递函数
所确定的传递函数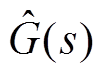 为
为
因此,通过输入信号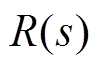 与输出信号
与输出信号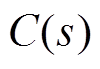 可推导出频率跟踪滤波器的系统传递函数
可推导出频率跟踪滤波器的系统传递函数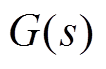 为
为
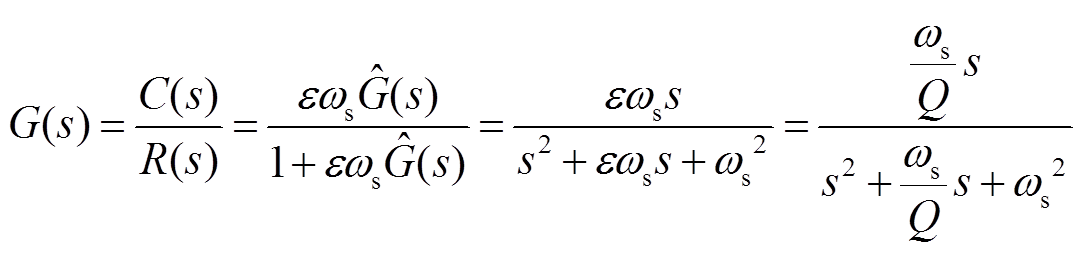 (11)
(11)
式中,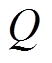 为该频率跟踪滤波器的带通品质因数,且满足
为该频率跟踪滤波器的带通品质因数,且满足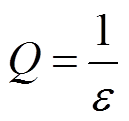 。
。
该滤波器的幅频特性为
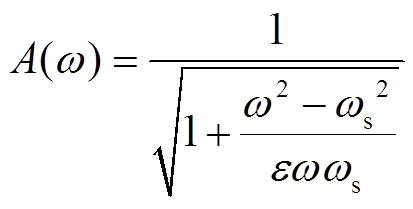 (12)
(12)
根据该滤波器的品质因数和幅频特性可知,在中心频率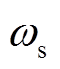 处,滤波器的增益取得最大值1。当频率小于或大于
处,滤波器的增益取得最大值1。当频率小于或大于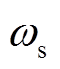 ,带通响应的幅值随着与中心频率差值的增大而减小。同时,随着电机转子电角速度
,带通响应的幅值随着与中心频率差值的增大而减小。同时,随着电机转子电角速度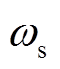 的变化,滤波器的中心频率也随之改变。该滤波器实现了对中心频率的跟踪,同时也对通频带内的基波信号实现了提取,滤除了霍尔矢量
的变化,滤波器的中心频率也随之改变。该滤波器实现了对中心频率的跟踪,同时也对通频带内的基波信号实现了提取,滤除了霍尔矢量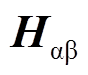 中正交分量的高次谐波信号。
中正交分量的高次谐波信号。
由于该带通频率跟踪滤波器的品质因数只与滤波器增益系数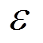 相关,于是,在转子电角速度变化时,滤波器的幅频特性与相频特性具有一致性。因此,在频率改变的情况下,可以有效提高滤波器的跟踪性能与带通响应性能。带通频率跟踪滤波器伯德图如图11所示。以转子电角速度
相关,于是,在转子电角速度变化时,滤波器的幅频特性与相频特性具有一致性。因此,在频率改变的情况下,可以有效提高滤波器的跟踪性能与带通响应性能。带通频率跟踪滤波器伯德图如图11所示。以转子电角速度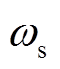 =100rad/s为例,对于不同品质因数
=100rad/s为例,对于不同品质因数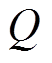 值,其滤波器的滚降程度和动态响应也有较大区别。随着
值,其滤波器的滚降程度和动态响应也有较大区别。随着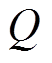 的增大,带通通频带逐渐变窄,增强了滤波效果,但滤波器的动态响应时间随之增加。
的增大,带通通频带逐渐变窄,增强了滤波效果,但滤波器的动态响应时间随之增加。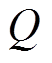 值减小时,滤波器的滤波效果与动态响应时间则与之相反。
值减小时,滤波器的滤波效果与动态响应时间则与之相反。
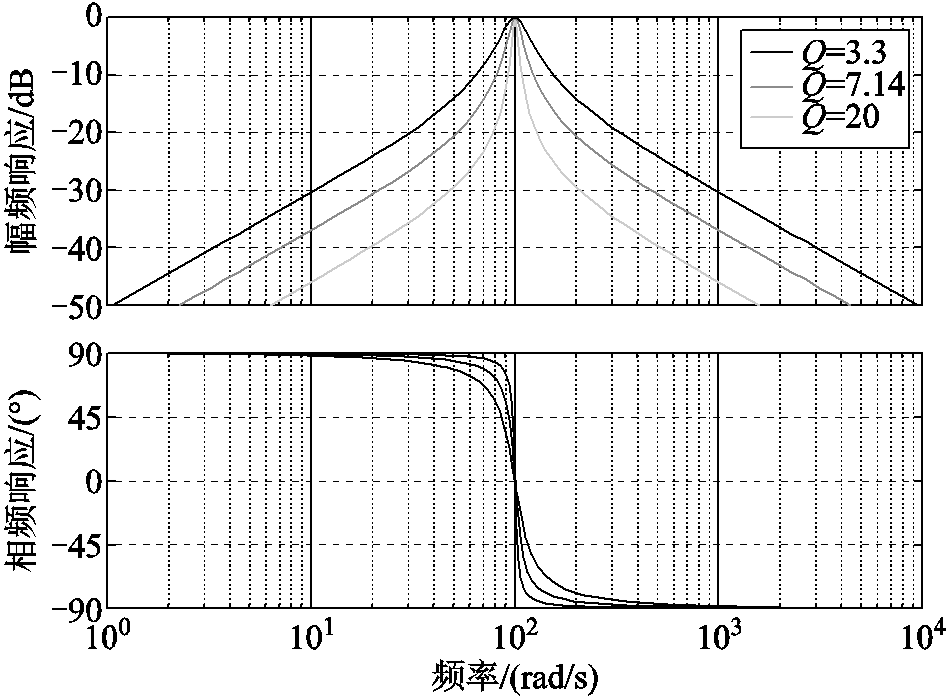
图11 带通频率跟踪滤波器伯德图
Fig.11 Bode plot of band-pass frequency tracking filter
考虑到在霍尔位置传感器安装位置偏移误差的情况下,基于T法估算的每个扇区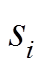 的转子电角速度会出现较大波动,但在整个霍尔周期中电机转子运行的电角度为定值,即
的转子电角速度会出现较大波动,但在整个霍尔周期中电机转子运行的电角度为定值,即
因此,在一个霍尔周期内,转子的平均电角速度不受霍尔位置传感器的安装位置偏移误差影响,转子的平均电角速度可利用式(14)估算得到。
![]() (14)
(14)
式中,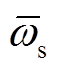 为一个霍尔信号周期内平均电角速度;
为一个霍尔信号周期内平均电角速度;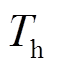 为霍尔位置传感器的输出周期。
为霍尔位置传感器的输出周期。
对于高速或多极对电机,平均电角速度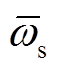 可近似作为电机的实时电角速度,故可以使用一个霍尔周期内的平均电角速度
可近似作为电机的实时电角速度,故可以使用一个霍尔周期内的平均电角速度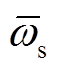 作为滤波器的跟踪频率。
作为滤波器的跟踪频率。
对于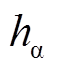 、
、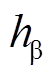 经带通频率跟踪滤波器后,输出的一对不含高次谐波的正交信号
经带通频率跟踪滤波器后,输出的一对不含高次谐波的正交信号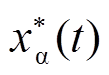 与
与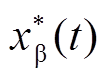 ,可通过正交锁相环(Phase Locked Loop, PLL)解耦,提取
,可通过正交锁相环(Phase Locked Loop, PLL)解耦,提取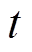 时刻下电机转子估算的速度信息
时刻下电机转子估算的速度信息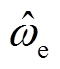 与位置角度信息
与位置角度信息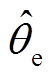 。
。
锁相环结构框图如图12所示,正交信号的估算误差为
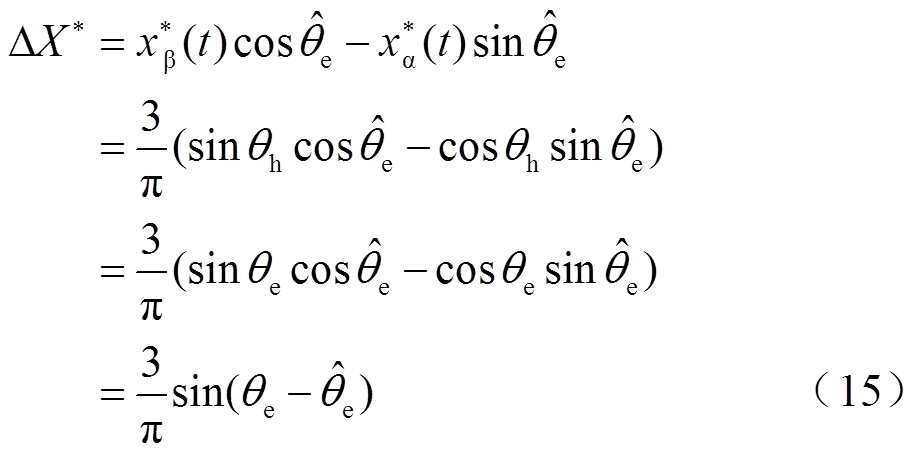
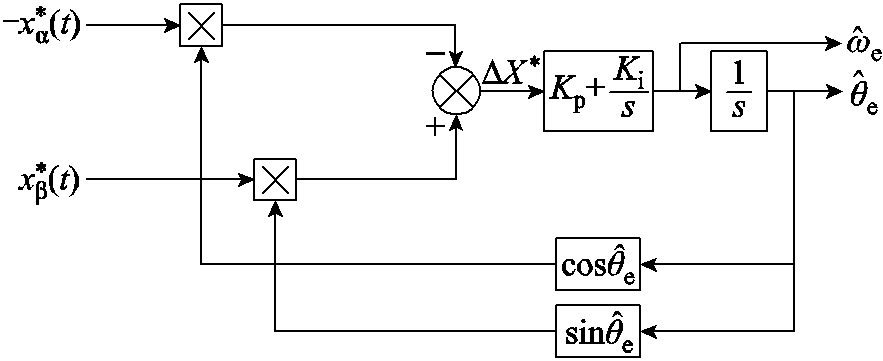
图12 锁相环结构框图
Fig.12 PLL structure block diagram
图12中,参数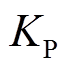 与
与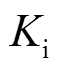 分别为锁相环PI的比例和积分参数,通过PI调节器,使得
分别为锁相环PI的比例和积分参数,通过PI调节器,使得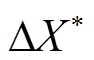 趋近于0。当
趋近于0。当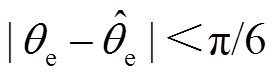 时,认为
时,认为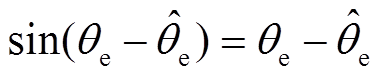 成立,因此当
成立,因此当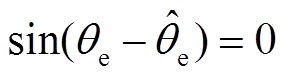 时,锁相环输出的估算转子电角度值
时,锁相环输出的估算转子电角度值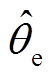 可认为是实际电机转子位置。
可认为是实际电机转子位置。
本文算法矢量控制框图如图13所示。可将基于带通频率跟踪滤波器法提取出电机的转子位置与速度信息作为电机矢量控制系统中的反馈信息,使得矢量控制系统在霍尔位置传感器发生安装偏移误差的情况下依然能够实现良好的控制效果。
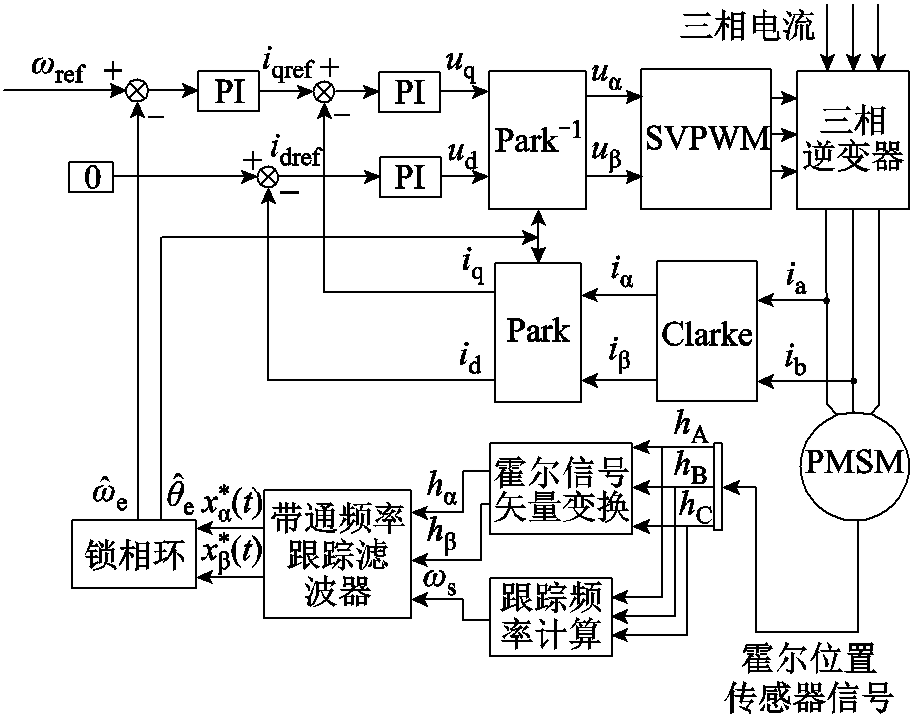
图13 本文算法矢量控制框图
Fig.13 The algorithm vector control block diagram of this paper
搭建的实验平台采用电机专用测试系统,并配有专用上位机操作界面,通过实验验证了文中提出的基于带通频率跟踪滤波器的PMSM转子位置与速度估算方法,系统的实验平台如图14所示。

图14 系统实验平台
Fig.14 System experiment platform
系统实验平台采用外转子式永磁同步电机,对应的实验电机参数见表2。
表2 永磁同步电机参数
Tab.2 PMSM parameter

参数数值 额定电压/V48 额定电流/A10.5 额定功率/W400 额定转矩/(N·m)4.5 空载额定转速/(r/min)1 500 极对数4
实验控制器采用STM32G431RBT6作为主控芯片,PWM开关频率设置为20kHz,控制器额定输入电压为48V,电机最大转速设置为1 000r/min,电机最大转矩为4.8N·m。通过制造电机三相霍尔位置传感器的机械角度偏移误差,使得A相霍尔位置传感器滞后偏移的机械角度为2.25°,B相霍尔位置传感器超前偏移的机械角度为3.37°,C相霍尔位置传感器超前偏移的机械角度为4.56°。
偏移误差前后霍尔矢量波形对比如图15所示,当永磁同步电机以1 000r/min匀速运行时,通过对比在霍尔位置传感器发生偏移误差前后的霍尔矢量正交分量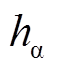 和
和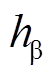 的输出波形可知,在霍尔位置传感器发生偏移误差时,输出的
的输出波形可知,在霍尔位置传感器发生偏移误差时,输出的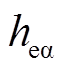 与
与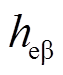 信号波形出现了明显的不对称畸变,此时,对
信号波形出现了明显的不对称畸变,此时,对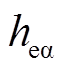 信号进行傅里叶变换,可得到
信号进行傅里叶变换,可得到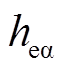 信号的频谱关系图。
信号的频谱关系图。
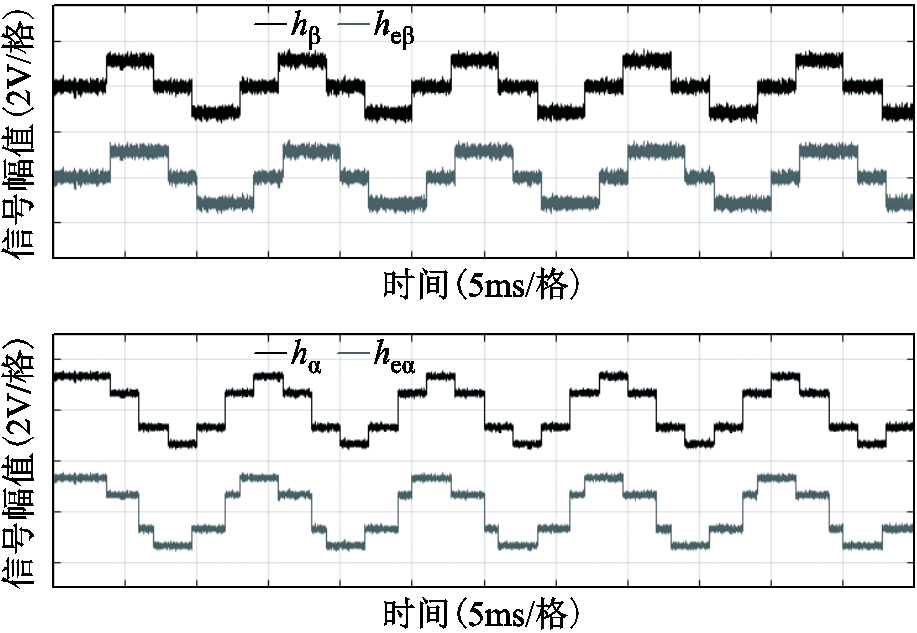
图15 偏移误差前后霍尔矢量波形对比
Fig.15 Hall vector waveforms comparison before and after offset error
偏移误差时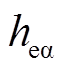 的谐波次序如图16所示,在
的谐波次序如图16所示,在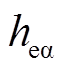 信号发生不对称畸变后,其含有的高次谐波成分也随之改变,其中畸变波形中主要冗余出:幅值为-16.28dB、频率为12kHz的3次谐波;幅值为-19.46dB、频率36kHz的9次谐波;幅值为-31.20dB、频率60kHz的15次谐波。但由于基波分量的幅值接近于0dB,远大于其余高次谐波的幅值,所以采用带通频率跟踪滤波器可以较好地实现对于不同转速下霍尔矢量信号基波分量的提取。
信号发生不对称畸变后,其含有的高次谐波成分也随之改变,其中畸变波形中主要冗余出:幅值为-16.28dB、频率为12kHz的3次谐波;幅值为-19.46dB、频率36kHz的9次谐波;幅值为-31.20dB、频率60kHz的15次谐波。但由于基波分量的幅值接近于0dB,远大于其余高次谐波的幅值,所以采用带通频率跟踪滤波器可以较好地实现对于不同转速下霍尔矢量信号基波分量的提取。
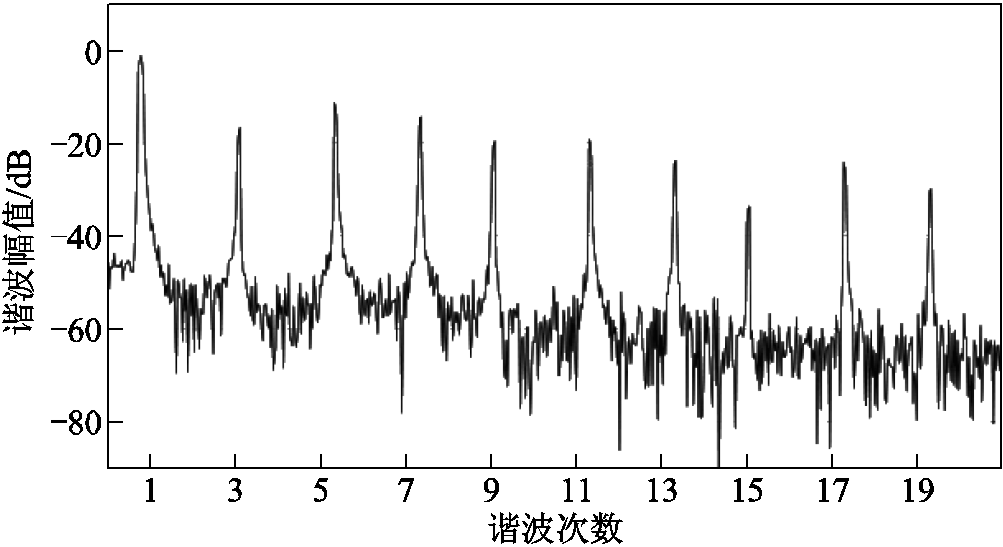
图16 偏移误差时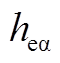 的谐波次序
的谐波次序
Fig.16 Harmonic order of 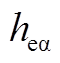 at the time of offset error
at the time of offset error
经滤波后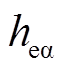 的谐波次序如图17所示,将
的谐波次序如图17所示,将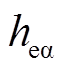 信号输入品质因数
信号输入品质因数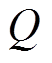 =7.14的带通频率跟踪滤波器后,其输出信号的频率成分具有明显改善,其余高次谐波幅值均被抑制在-40dB以下,有效地滤除了除基波分量外的其他高次谐波分量,较好地实现对其他高次谐波分量的抑制与对基波信号的提取。
=7.14的带通频率跟踪滤波器后,其输出信号的频率成分具有明显改善,其余高次谐波幅值均被抑制在-40dB以下,有效地滤除了除基波分量外的其他高次谐波分量,较好地实现对其他高次谐波分量的抑制与对基波信号的提取。
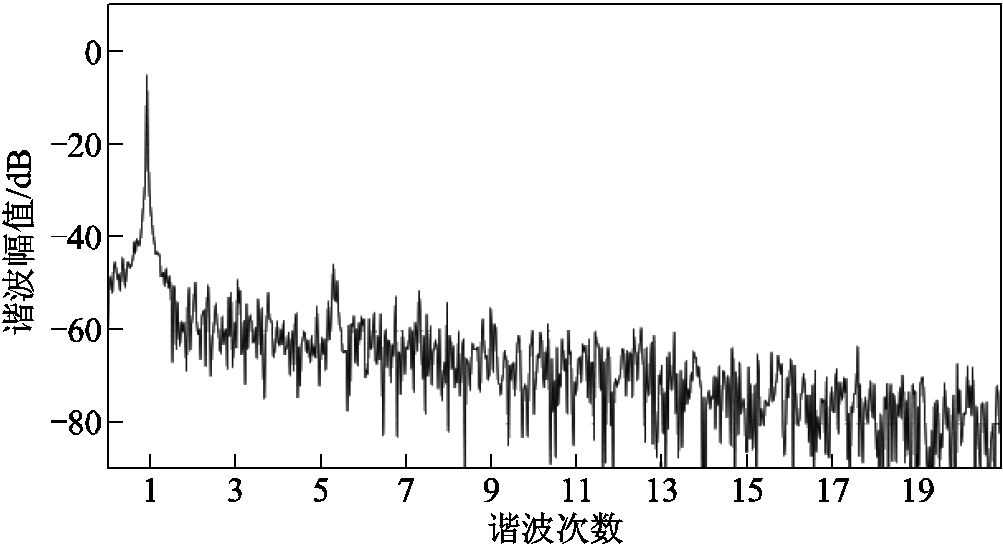
图17 经滤波后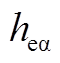 的谐波次序
的谐波次序
Fig.17 Harmonic order of 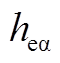 after filtering
after filtering
图18针对电机在1 000r/min转速下,将传统T法转子位置估算结果与基于带通频率跟踪滤波器下的转子位置估算结果进行对比可知,前者在霍尔位置传感器发生偏移误差时转子估算结果出现较大幅值的波形畸变,在电角度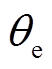 =(2k+1)
=(2k+1)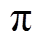 处出现较大的估算误差,误差电角度取值位于39.4°~43.5°之间,不利于电机进行平滑的转速控制。后者算法估算的转子位置与理想位置误差较小,误差电角度取值小于5.5°。波形平滑连续,相位跟踪度较好。
处出现较大的估算误差,误差电角度取值位于39.4°~43.5°之间,不利于电机进行平滑的转速控制。后者算法估算的转子位置与理想位置误差较小,误差电角度取值小于5.5°。波形平滑连续,相位跟踪度较好。
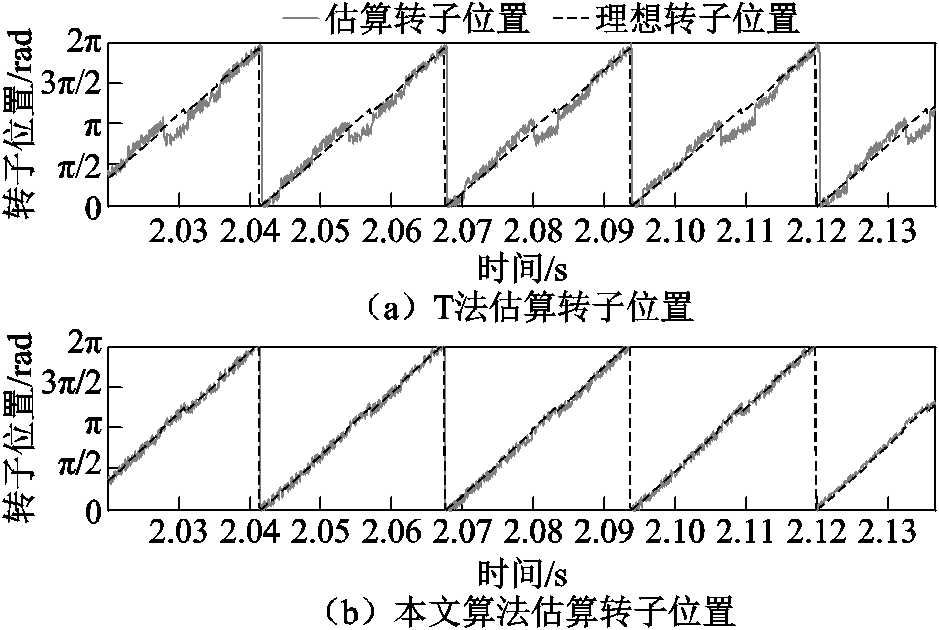
图18 霍尔位置传感器偏移下转子位置估算结果对比
Fig.18 Comparison of rotor position estimation results under Hall position sensor offset
图19~图21针对三种不同目标恒转速,在上述霍尔位置传感器偏移误差的情况下,将传统T法转速估算法与基于带通频率跟踪滤波器的转速估算法的估算效果进行比较,传统T法转速估算在恒转速100r/min下转速误差为-8~+8r/min,与基于带通频率跟踪滤波器的转速估算法的估算效果类似。然而,传统T法转速估算在恒转速300r/min与恒转速1 000r/min下转速误差出现较大的波动,估算转速误差分别位于±20r/min与±100r/min之间。而基于带通频率跟踪滤波器的转速估算法的估算转速误差分别位于±5r/min与±15r/min之间。在不同转速区间中,基于带通频率跟踪滤波器的转速估算结果均优于基于传统T法转速估算结果。
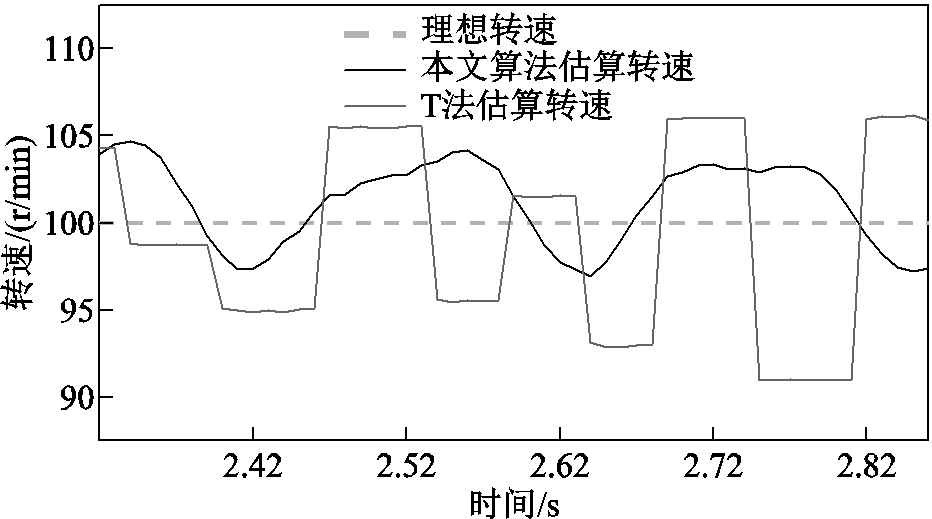
图19 电机100r/min下补偿控制前后转速对比
Fig.19 Speed comparison before and after motor 100r/min under compensation control
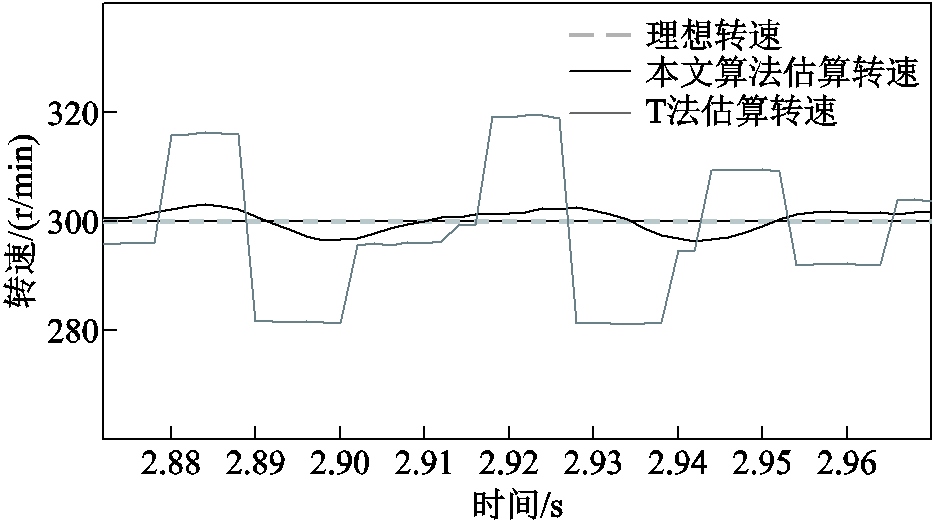
图20 电机300r/min下补偿控制前后转速对比
Fig.20 Speed comparison before and after motor 300r/min under compensation control
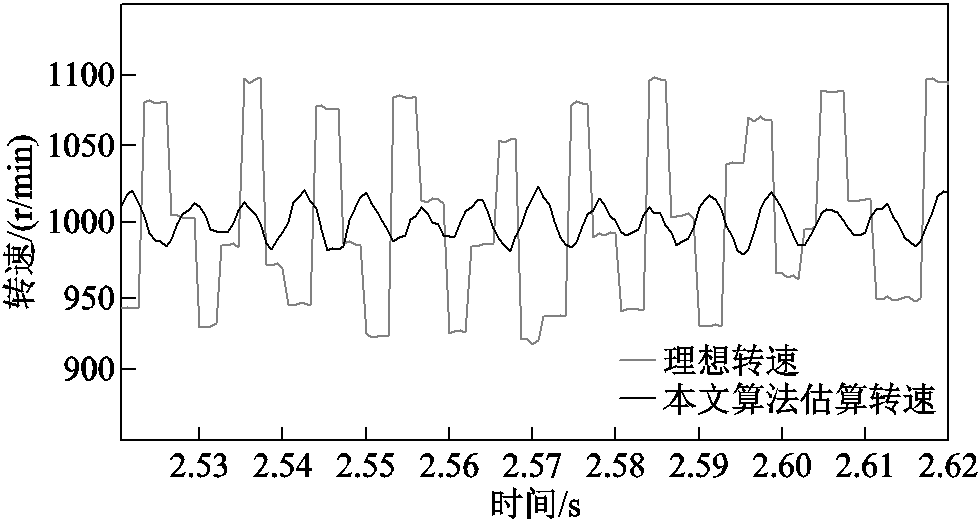
图21 电机1 000r/min下补偿控制前后转速对比
Fig.21 Speed comparison before and after motor 1 000r/min under compensation control
在设定的全速度区间内,进行0~1 000r/min加速实验,结果如图22所示。在设定的全速度区间内,进行300~1 000r/min加速实验与1 000~300r/min的减速实验,结果如图23所示。传统T法转速估算曲线与理想转速曲线相比具有较大的转速估算误差。加速过程中,随着转速增加,在加速超调区间内转速正向误差大于120r/min。而基于带通频率跟踪滤波器的转速估算法的估算转速误差则较小,在加速运行过程中、减速运行过程中与匀速运行过程中转速曲线均无较大波动,电机在运行过程中具有良好的转速稳定性。
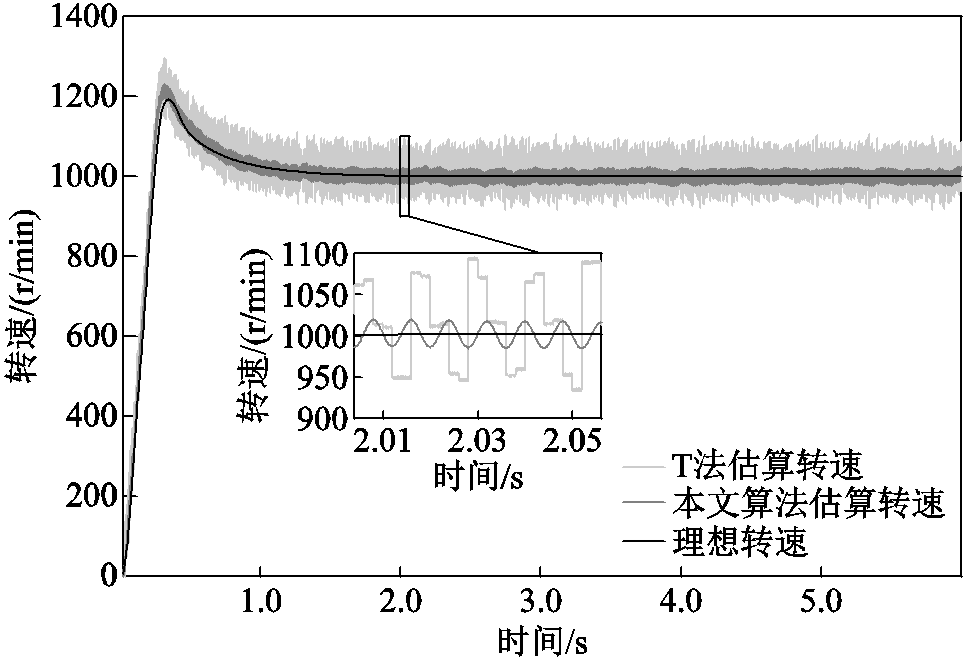
图22 全速度区间内加速曲线对比
Fig.22 Comparison of speed curves in the full speed range
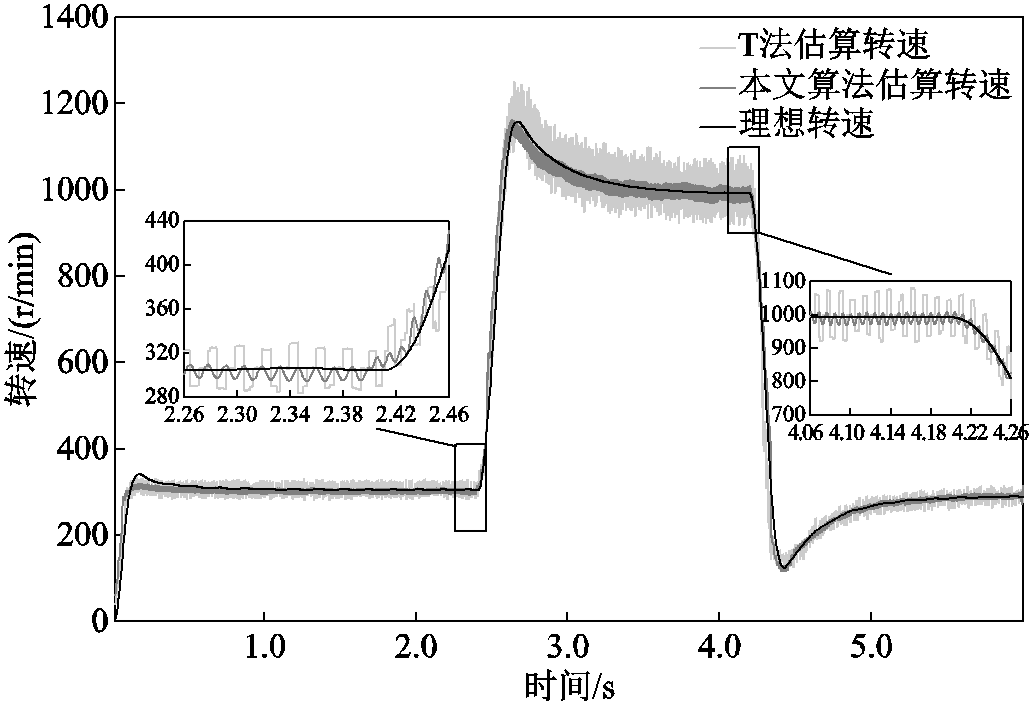
图23 全速度区间内加减速曲线对比
Fig.23 Comparison of acceleration and deceleration curves in the full speed range
两种算法在永磁同步电机在加速过程与减速过程中估算的转子位置结果如图24所示。从图24中可以看出,与传统T法估算的转子位置结果相比,采用基于带通频率跟踪滤波器的转子位置估算法,在霍尔位置传感器安装偏移误差的情况下,转子位置估算结果准确度较高,在加速与减速过程中可以得到连续平滑且较为准确的转子位置,具有良好的动态性能,验证了该转子位置估算方法的有效性。
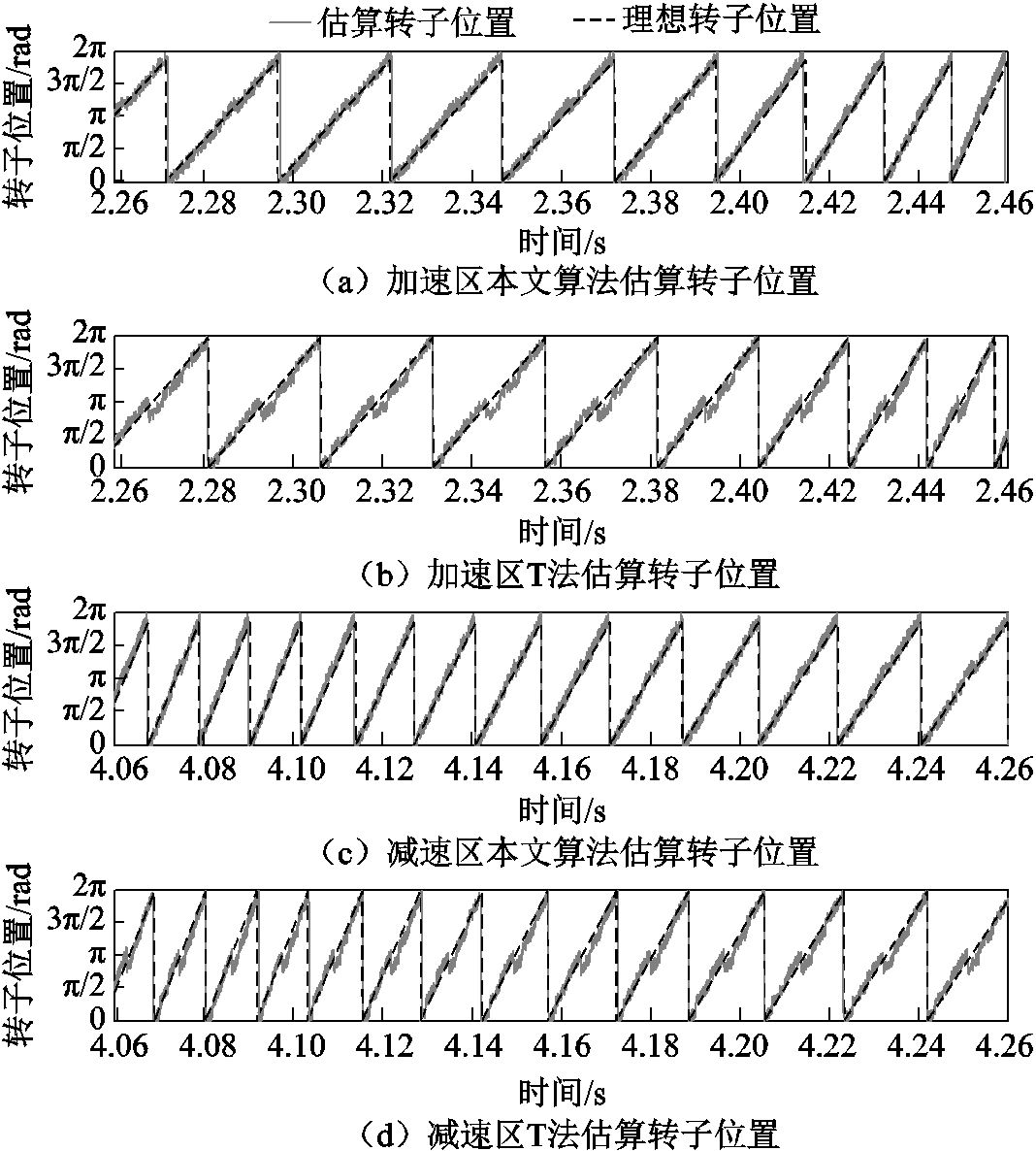
图24 霍尔位置传感器偏移下加减速过程中的转子位置估算结果对比
Fig.24 Comparison of rotor position estimation results during acceleration and deceleration under Hall position sensor offset
两种转速估算法在控制电机运行过程中q轴电流的波形曲线如图25和图26所示。本文所提出的补偿控制算法相较于基于传统T法测速的矢量控制算法在霍尔位置传感器发生安装偏移误差时,q轴电流具有更好的幅值稳态性。其中,在电机转矩为1.43N·m时,补偿控制前q轴电流的峰-峰值为12.6A,补偿控制后q轴电流的峰-峰值为5.8A。在补偿控制后电机在实际运行过程中,具有更稳定的转速、转矩,和更小的噪声,有效减小了在霍尔位置传感器发生偏移误差下,产生的功率波动,提高了永磁同步电机矢量控制的稳定性。
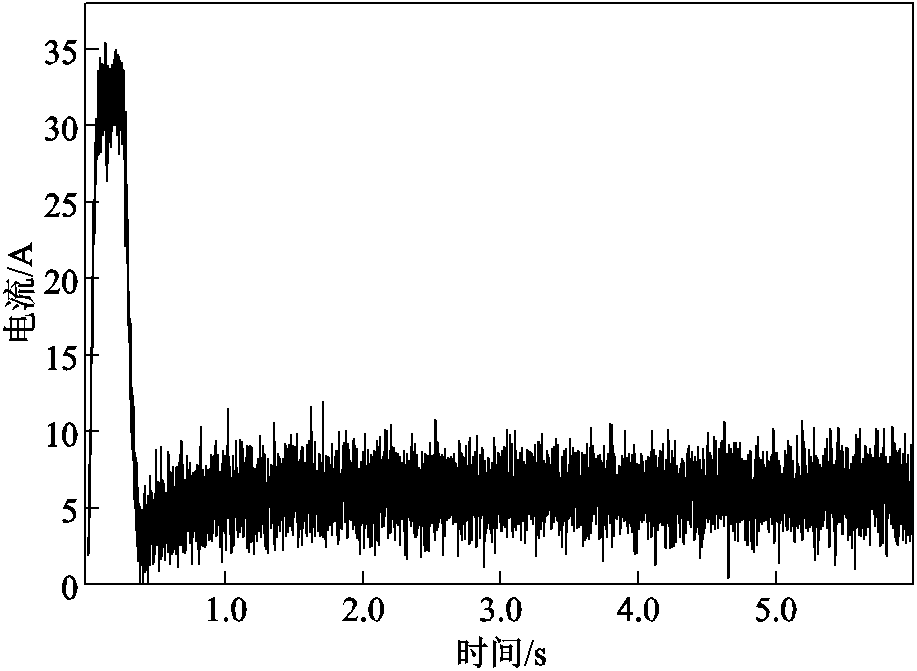
图25 偏移误差时补偿控制前iq曲线
Fig.25 iq current curve before compensation control when offset error
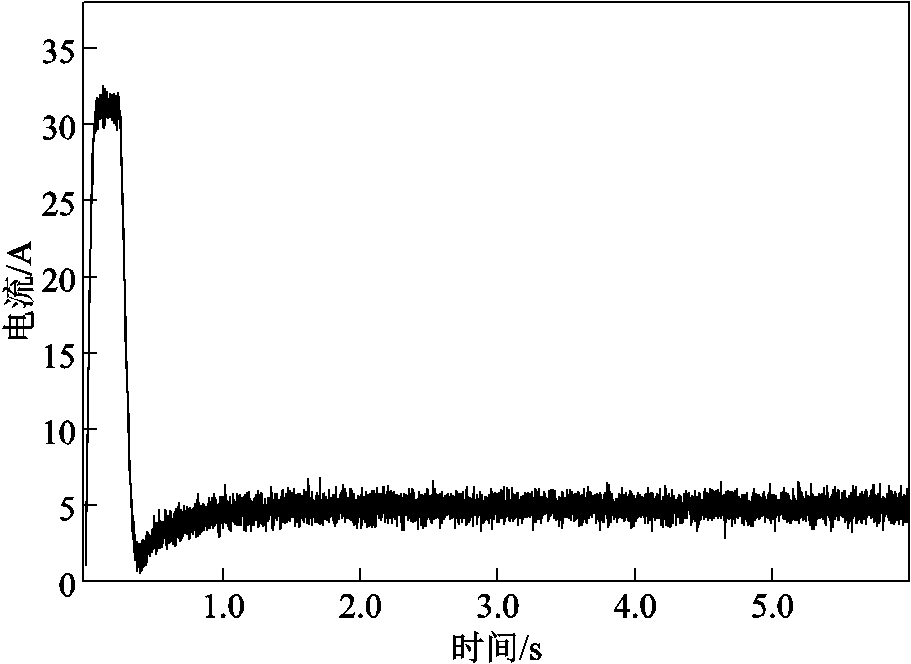
图26 偏移误差时补偿控制后iq曲线
Fig.26 iq current curve before and after compensation control when offset error
在负载突变的情况下,两种转速估算法在控制电机运行过程中,q轴电流与转速波形曲线的变化如图27和图28所示。当电机在加载过程中,转矩从1.43N·m突变至4.50N·m,基于传统T法测速的矢量控制下的q轴平均峰值电流从7.7A突变至12.4A,转速从均值1 000r/min下降至均值890r/min。本文所提出的补偿控制算法相较于基于传统T法测速的矢量控制算法在霍尔位置传感器发生安装偏移误差时,q轴平均峰值电流值从6.3A突变至8.5A,平均转速从均值1 000r/min下降至980r/min。
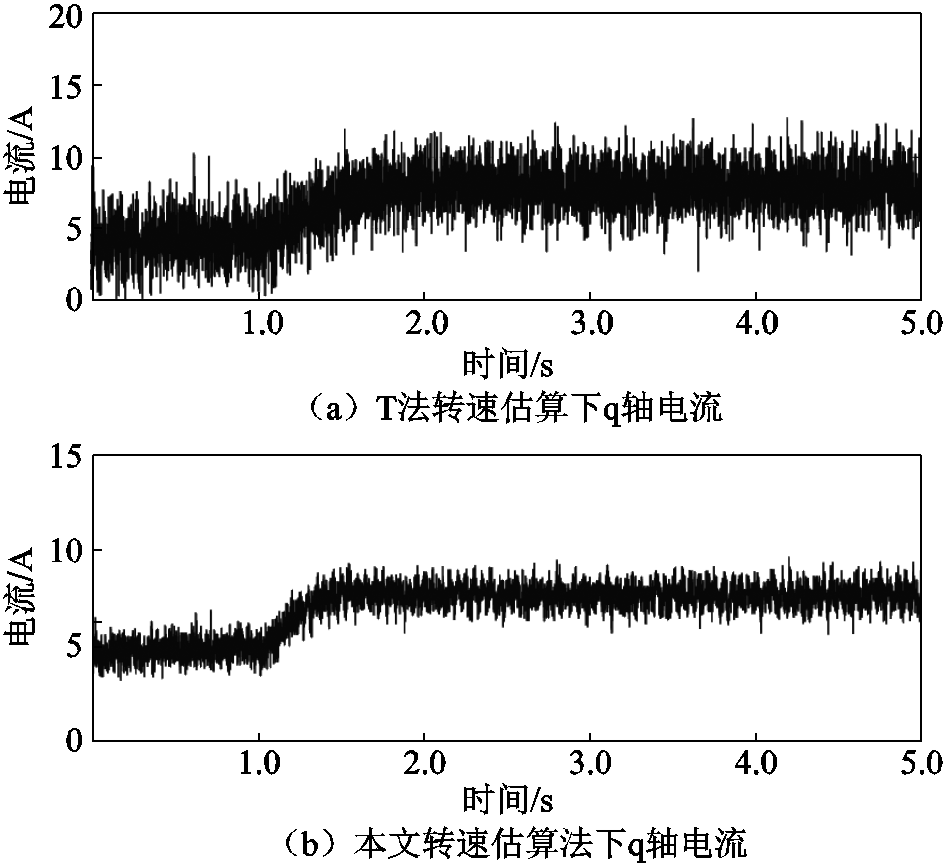
图27 负载突变时iq变化曲线
Fig.27 Change curves of iq current when the load changes suddenly
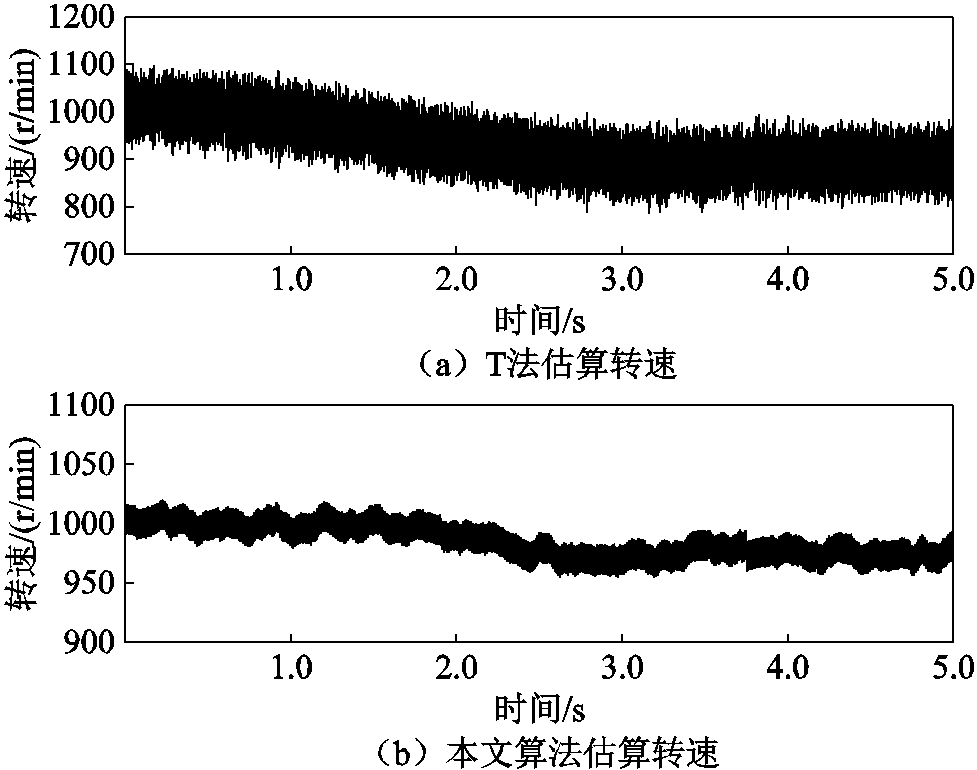
图28 负载突变时转速变化曲线
Fig.28 Speed changes curves when load changes suddenly
可见,在霍尔位置传感器发生安装偏移误差时,由于基于传统T法测速的矢量控制下的q轴平均峰值电流过大,导致控制器发生严重的过热、过电流,导致电机发生转速波动、抖振与转速下降。而在基于带通频率跟踪滤波器的转速与转子位置估算算法下的矢量控制q轴平均峰值电流相对较小,转子位置与转速估算更加准确,延长了电机使用寿命,增强了电动助力车控制系统的稳定性。
本文针对电动助力车用永磁同步电机发生霍尔位置传感器安装偏移情况下电机运行异常的问题,提出了一种基于带通频率跟踪滤波器的转子位置与速度估算方法,可提高电机运行的可靠性和稳定性。通过实验得出以下结论:
1)利用该转子位置与转速估算法,可使电动助力车控制系统在电机发生霍尔位置传感器安装偏移的工况下,实现对驱动电机的正常控制。
2)该转子位置与转速估算法通过对霍尔信号进行矢量变换,使用带通频率跟踪滤波器提取霍尔矢量中含有的转子位置信息的方式,有效地提高了对电机转子位置与转速估算的精度。
3)通过对比基于传统T法转速估算方法,该新型容错控制算法在转速补偿控制性能与电流补偿控制性能上均优于传统T法转速估算下的矢量控制。有效地避免了驱动电机在霍尔位置传感器安装偏移情况下产生的抖振、过电流等异常情况,提高了驱动电机的使用寿命。
参考文献
[1] Petrone N, Meneghetti G. Fatigue life prediction of lightweight electric moped frames after field load spectra collection and constant amplitude fatigue bench tests[J]. International Journal of Fatigue, 2019, 127: 564-575.
[2] Hu Feng, Lü Donglai, Zhu Jie, et al. Related risk factors for injury severity of e-bike and bicycle crashes in Hefei[J]. Traffic Injury Prevention, 2014, 15(3): 319-323.
[3] 倪启南, 杨明, 徐殿国, 等. 低分辨率位置传感器永磁同步电机精确位置估计方法综述[J]. 电工技术学报, 2017, 32(22): 70-81.
Ni Qinan, Yang Ming, Xu Dianguo, et al. Review of precise position estimation method of PMSM with low-resolution position sensor[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 70-81.
[4] Song Ziyou, Li Jianqiu, Ouyang Minggao, et al. Rule-based fault diagnosis of Hall sensors and fault-tolerant control of PMSM[J]. Chinese Journal of Mechanical Engineering, 2013, 26(4): 813-822.
[5] Park J S, Choi J H, Lee J. Compensation method of position signal error with misaligned Hall-effect sensors of BLDC motor[J]. Journal of Electrical Engineering and Technology, 2016, 11(4): 889-897.
[6] Lee D M. Position estimator employing Kalman filter for PM motors driven with binary-type Hall sensors[J]. Journal of Electrical Engineering and Technology, 2016, 11(4): 931-938.
[7] Reigosa D, Fernandez D, González C, et al. Permanent magnet synchronous machine drive control using analog Hall-effect sensors[J]. IEEE Transactions on Industry Applications, 2018, 54(3): 2358-2369.
[8] 张涵, 王凯, 李健, 等. 基于开关型霍尔的交替极永磁电机位置估算策略[J]. 中国电机工程学报, 2020, 40(7): 2377-2384, 2416.
Zhang Han, Wang Kai, Li Jian, et al. Position estimation strategy of consequent-pole PM machine based on binary Hall sensor[J]. Proceedings of the CSEE, 2020, 40(7): 2377-2384, 2416.
[9] 刘细平, 胡卫平, 丁卫中, 等. 永磁同步电机多参数辨识方法研究[J]. 电工技术学报, 2020, 35(6): 1198-1207.
Liu Xiping, Hu Weiping, Ding Weizhong, et al. Research on multi-parameter identification method of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1198-1207.
[10] 付东学, 赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报, 2020, 35(4): 717-723.
Fu Dongxue, Zhao Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723.
[11] Manyala J O, Fritz T, Atashbar M Z. Integration of triaxial Hall-effect sensor technology for gear position sensing in commercial vehicle transmissions[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(3): 664-672.
[12] Preindl M, Schaltz E. Sensorless model predictive direct current control using novel second-order PLL observer for PMSM drive systems[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4087-4095.
[13] 李永刚, 王罗, 李俊卿, 等. 基于多源信息融合的同步发电机转子绕组匝间短路故障识别[J]. 电力系统自动化, 2019, 43(16): 162-167, 191.
Li Yonggang, Wang Luo, Li Junqing, et al. Identification of inter-turn short-circuit fault in rotor windings of synchronous generator based on multi-source information fusion[J]. Automation of Electric Power Systems, 2019, 43(16): 162-167, 191.
[14] Park J S, Lee K D. Online advanced angle adjustment method for sinusoidal BLDC motors with misaligned Hall sensors[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8247-8253.
[15] 张懿, 张明明, 魏海峰, 等. 基于霍尔传感器的永磁同步电机高精度转子位置观测[J]. 电工技术学报, 2019, 34(22): 4642-4650.
Zhang Yi, Zhang Mingming, Wei Haifeng, et al. High precision rotor position observation of permanent magnet synchronous motor based on Hall sensors[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4642-4650.
[16] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.
Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet synchronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.
[17] Zhang Qian, Feng Ming. Combined commutation optimisation strategy for brushless DC motors with misaligned Hall sensors[J]. IET Electric Power Applications, 2018, 12(3): 301-307.
[18] Ban D, Lee S, Hong J. Rotor position estimation of permanent magnet synchronous motors using low-resolution sensors[J]. International Journal of Fuzzy Systems, 2017, 19(1): 78-85.
[19] Tesch T R, Lorenz R D. Disturbance torque and motion state estimation using low resolution position interfaces[C]//Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, 2006: 917-924.
[20] Kim S Y, Choi C, Lee K, et al. An improved rotor position estimation with vector-tracking observer in PMSM drives with low-resolution Hall-effect sensors[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4078-4086.
[21] Liu Gang, Chen Baodong, Song Xinda. High-precision speed and position estimation based on Hall vector frequency tracking for PMSM with bipolar Hall-effect sensors[J]. IEEE Sensors Journal, 2019, 19(6): 2347-2355.
Permanent Magnet Synchronous Motor Rotor Position and Speed Estimation Methodology Based on Band-Pass Frequency Tracking Filter
Abstract In the permanent magnet synchronous motor (PMSM) control system for electric mopeds, method for estimating the position and speed of the motor rotor based on the band-pass frequency tracking filter are proposed to solve the problem of the deviation of the installation position of the Hall position sensor. The algorithm converts the three-phase Hall signal into a Hall vector through the coordinate transformation, and extracts the rotor position information of the motor in the Hall vector via a band-pass frequency tracking filter and a phase-locked loop, so as to the correct estimation of the rotor position and speed information of the permanent magnet synchronous motor has been realized on the condition of the installation position offset of the Hall position sensor. Through experimental verification, the algorithm effectively reduces the fluctuation of the motor speed and current when the Hall position sensor is installed at a position offset, and improves the reliability and stability of the control system.
keywords:Electric moped, permanent magnet synchronous motor, Hall position sensor, installation position deviation, band pass frequency tracking filter
DOI:10.19595/j.cnki.1000-6753.tces.210717
中图分类号:TM351
国家自然科学基金(51977101, 62276117)和江苏省研究生科研与实践创新计划(SJCX21_1742)资助项目。
收稿日期 2021-05-19
改稿日期 2021-08-20
李垣江 男,1981年生,博士,副教授,研究方向为电机故障诊断、视觉传感。E-mail:liyuanjiang@just.edu.cn(通信作者)
苗奎星 男,1996年生,硕士研究生,研究方向为电机低成本控制。E-mail:mkxjust@foxmail.com
(编辑 赫蕾)