摘要 基于磁场感应的无线电能传输（IPT）系统需要反馈控制实现稳定的输出，这依赖于一个精确且简单的小信号模型。近些年来，扩展描述函数法（EDF）在谐振变换器建模问题中有广泛运用。由于IPT系统的本质为高阶谐振变换器，因此该方法可以应用于IPT系统的建模中。但是由于IPT系统中包含大量谐振元件，直接通过EDF方法得到的模型往往具有较高阶数，通过一种基于电路化简的方法对电路中的谐振元件模型进行化简，可以同时保证模型的准确性与精简性。该文以LCC-S补偿的IPT系统为例，阐述化简方法。该方法也可以推广至其他高阶IPT系统中。
关键词：感性电能传输 等效电路模型 扩展描述函数 降阶模型
随着温室效应的加剧，电动汽车的推广逐渐受到各国政府的重视。对车载电池的供电是电动车相关研究领域中的热门方向之一。无线充电作为有线充电的一种补充，正逐渐被引入电动车充电领域。近些年来，不少课题组开始研究感性电能传输（Inductive Power Transfer, IPT）在电动汽车充电中的应用[1-3]。这种新型能量传输方式基于谐振耦合现象，并利用近场磁场进行非辐射性、中距离输电[4-6]。该电能传输方式无需电气接触，因此有更高的便利性与安全性。
为了提高IPT系统的传输能力，需要在系统中增加补偿电路以减少无功功率。增设补偿电路还可以使系统实现与负载无关的恒压输出或者恒流输出。奥克兰大学的课题组提出了四种基本结构的补偿电路[7]，即串联-串联（S-S）、串联-并联（S-P）、并联-并联（P-P）和并联-串联（P-S）。近些年来有课题组对于各种高阶谐振补偿网络进行了分析与设计[8]，通过增加谐振元件个数可以增加系统设计的自由度。文献[9]基于与负载无关的IPT系统，设计了一个两级架构的无线快充系统，但是该系统为开环系统，缺少控制器使其达到稳定。
为实现IPT系统的输出目标，需要基于小信号模型设计反馈控制器，确保稳定性的同时实现较高的控制带宽。对于经典的脉冲宽度调制（Pulse Width Modulation, PWM）变换器，基于平均值概念的小信号模型已经十分成熟[10]，而另一种DC-DC谐振变换器，平均值模型却不适用。这是因为在谐振变换器中，谐振腔内的电流以及电压的平均值为零。对于谐振变换器的建模问题，基于基波近似的扩展描述函数法（Extended Describing Function, EDF）是目前最为成功的方法[11]。
IPT系统本质为谐振变换器，因此谐振变换器的建模方法也可以应用于IPT系统中。由于存在高阶补偿电路，IPT系统中含有较多的谐振元件。当EDF应用于IPT系统中，获得的往往是一个高阶模型。即使是最简单的串联-串联补偿系统，其小信号模型也为9阶[12]。因此如何降阶是目前IPT小信号模型研究中的难点。文献[13]将原本11阶的系统降为2阶，文献[14]将9阶系统降为4阶，但是上述方法都是基于数值方法，不具有一般性。
本文提出一种基于电路原理的IPT小信号模型化简与降阶方法，相比于以往的方法，该方法更加具有一般性与直观性。本文以LCC-S补偿IPT系统为例，首先建立输入到输出的全阶小信号模型，该系统为13阶系统；之后通过电路上的近似对模型进行降阶，使得原本13阶的系统简化为7阶的系统。模型中能够直接反映耦合系数对传统函数的影响。这种降阶方法具有通用性，可以应用于其他IPT系统中。最后本文将通过仿真与实验对所提出的模型进行验证。
本文将首先对LCC-S补偿的IPT系统进行稳态分析，该系统结构如图1所示。该IPT系统包含逆变器、发射侧补偿电路、耦合线圈、接收侧补偿电路和整流器。其中，Lp和Ls分别为发射线圈和接收线圈；L1、C1和Cp构成了发射侧补偿电路；Cs作为接收侧补偿电路。上述LCC-S补偿的IPT系统在式（1）所示的条件下可以实现与负载无关的恒压输出。
图1 LCC-S补偿IPT系统
Fig.1 An IPT system using LCC-S compensation
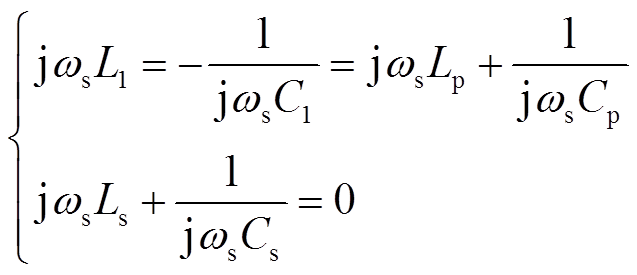（1）
式中，ωs为开关信号的角频率。在上述条件下，可以得到使用全桥逆变器时，系统的电压增益为
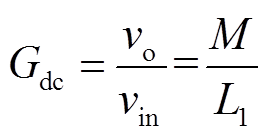（2）
式中，
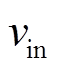和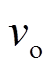
分别为系统的输入和输出电压；M为发射线圈与接收线圈的互感。若使用半桥逆变器，则增益为上述增益的1/2。
式（1）和式（2）描述了系统的稳态特性，无法表现系统的动态特性。为了评估系统控制的稳定性，小信号模型是必不可少的。接下来将推导系统的小信号模型。本文将利用EDF分别对系统中逆变器、谐振元件和整流器进行建模，并将所有部分组合得到最终的模型。
IPT系统中的逆变器的作用是将输入的直流信号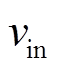和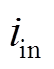
转换为频率fs的方波，可以把输出的方波近似为基波
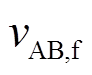和
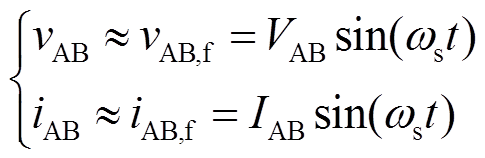（3）
式中，VAB和IAB为AB两端的电压和电流幅值，可以通过傅里叶变换得到其与输入电压Vin和输入电流Iin的关系，即
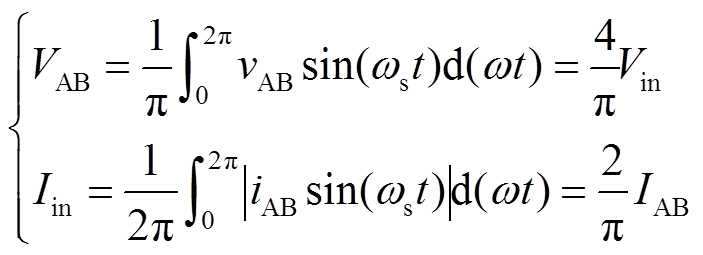（4）
当考虑系统出现扰动时，有
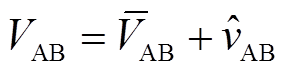（5）
式中，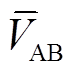
为电压的平均值；
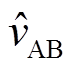为电压的扰动。本文后续出现的变量均采用这种表述方法。类似地，输入电压和电流可以表示为
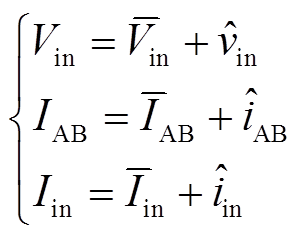（6）
通过式（4）和式（6）可以得到小信号电压增益为
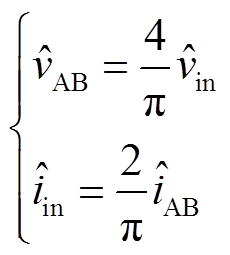（7）
因此，可以获得逆变器的等效小信号电路模型如图2所示。上述分析是基于全桥逆变器，若考虑半桥逆变器，则
。
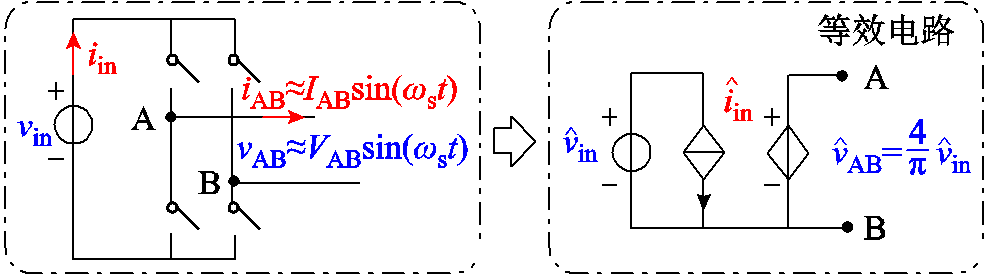
图2 全桥逆变器的小信号模型
Fig.2 Small-signal model of the full-bridge inverter
IPT系统中整流器的建模思路与逆变器相同。逆变器与整流器波形如图3所示。整流输入电压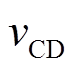
可以近似为基波
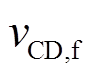，但由于逆变器与整流器存在相位差Φ，系统必须设置一个参考相位。本文以逆变的电压作为参考。因此整流器的电压电流可以表示为
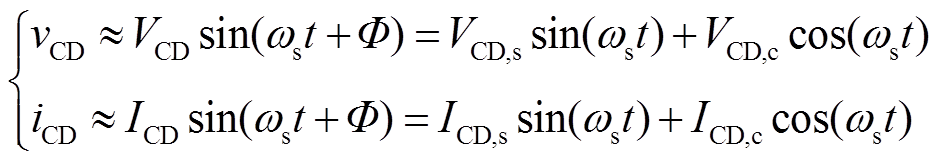（8）
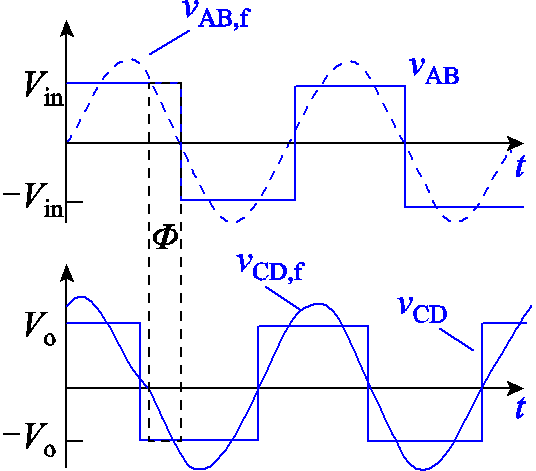
图3 逆变器与整流器波形
Fig.3 Typical waveforms for inverter and rectifier
式（8）将电压与电流分为正余弦两个部分，VCD,s和ICD,s分别为电压与电流正弦分量的幅值；同样地，VCD,c和ICD,c分别为电压与电流余弦分量的幅值；下标“s”和“c”分别代表各物理量的正弦和余弦部分。因此相位差Φ可以用电流iCD的正、余弦分量幅值表示，即tanΦ=ICD,c/ICD,s。式（8）中电压的正弦与余弦分量可以通过傅里叶变换求得
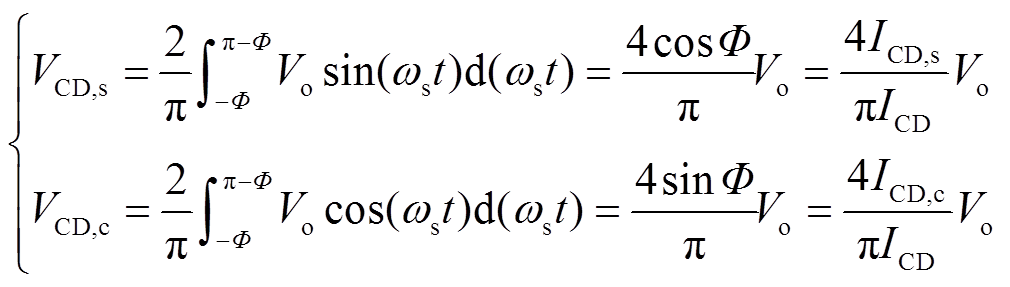（9）
整流桥输出电流ir=|iCD|，因此ir可以用直流量Ir表示，则有
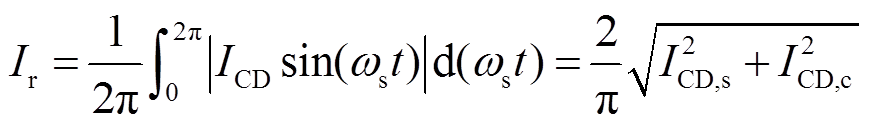（10）
当考虑小信号扰动时，式（9）和式（10）中的变量可以表示为
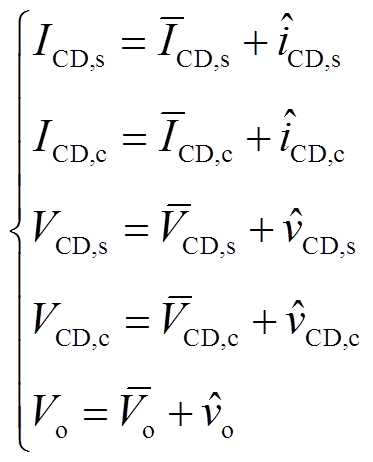（11）
对式（9）和式（10）在稳态处进行泰勒展开，并消去直流分量，可以得到在频率满足式（1）条件下整流器的小信号关系式为
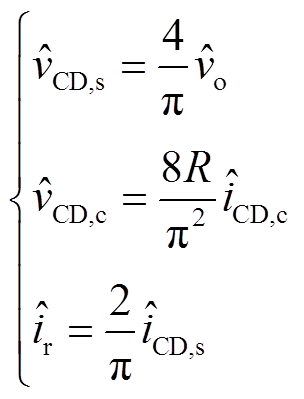（12）
式中，R为负载电阻。
根据式（11）可以得到逆变器的小信号模型如图4所示。
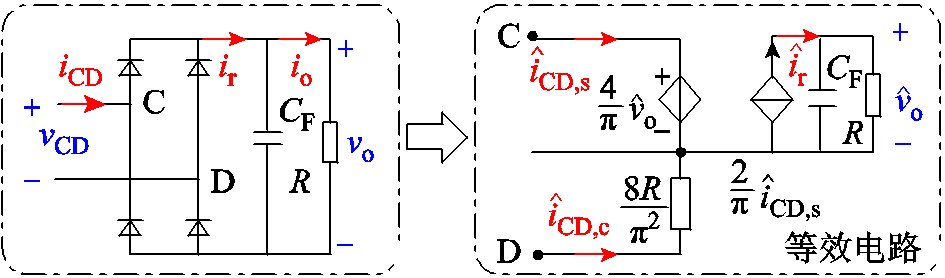
图4 逆变器小信号模型
Fig.4 Small-signal model of the rectifier
IPT系统中的谐振元件包含补偿电容、补偿电感以及耦合线圈，其中耦合线圈可以使用受控源模型转化为电感与受控电压源。利用EDF可以对电感和电容分别进行建模。由于电感和电容在电流电压上具有对称性，下面仅以电感小信号模型为例。
对电感电流与电压进行基波近似，假设电感电压vL与电感电流iL分别为
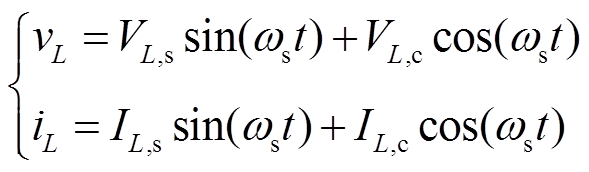（13）
式中，VL,s、VL,c、IL,s和IL,c分别为电感电压和电流的正余弦分量的幅值。在稳态系统中VL,s等效为定值，而当考虑瞬态时，VL,s为动态值。根据电感电压与电流的关系可以得到各分量的动态关系为
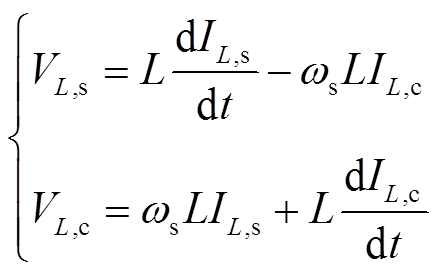（14）
当考虑小信号扰动时，例如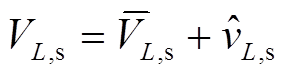
，可以得到系统电感电压电流的小信号关系式为
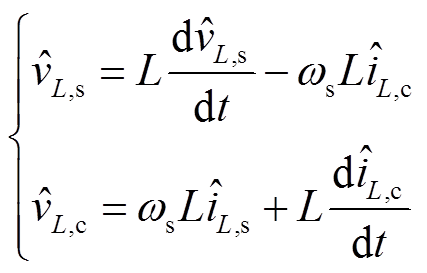（15）
同理，可以得到电容电压电流的小信号关系式为
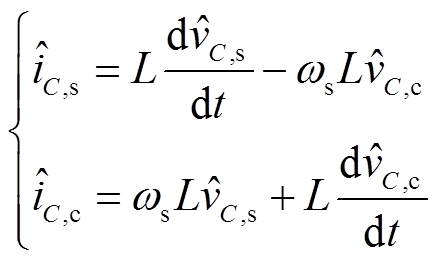（16）
因此电感与电压的小信号等效模型如图5所示。图中小信号模型包含了正弦部分与余弦部分，并且通过受控源与另外一条支路产生耦合。
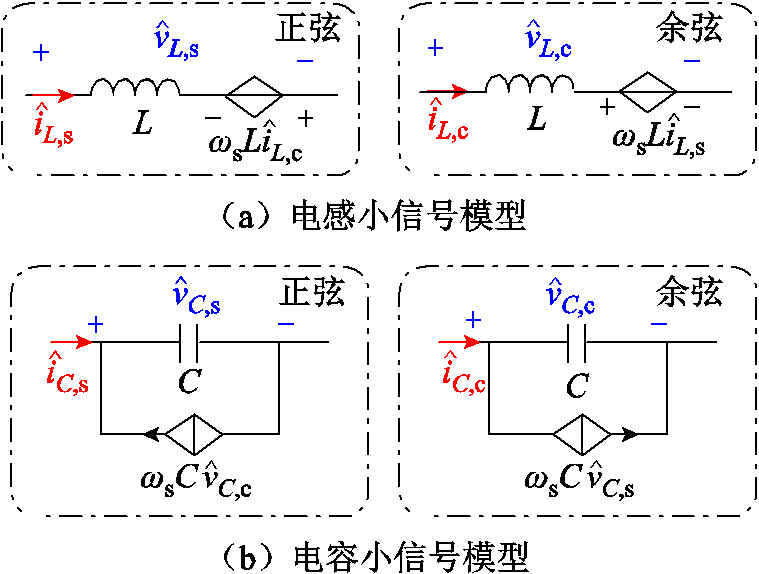
图5 电感电容小信号模型
Fig.5 Small-signal model of inductor and capacitor
IPT系统中受控电压源模型也可利用类似方法得到，因篇幅问题这里就不详细叙述。
将以上所获得的小信号等效模型相连，则可以得到系统完整的小信号模型，如图6所示。该模型是一个13阶系统，可以较为准确地预测输入到输出的小信号增益。但由于系统阶数过高，求解传递函数过程变得极为复杂。因此需要一种通用的降阶方法。
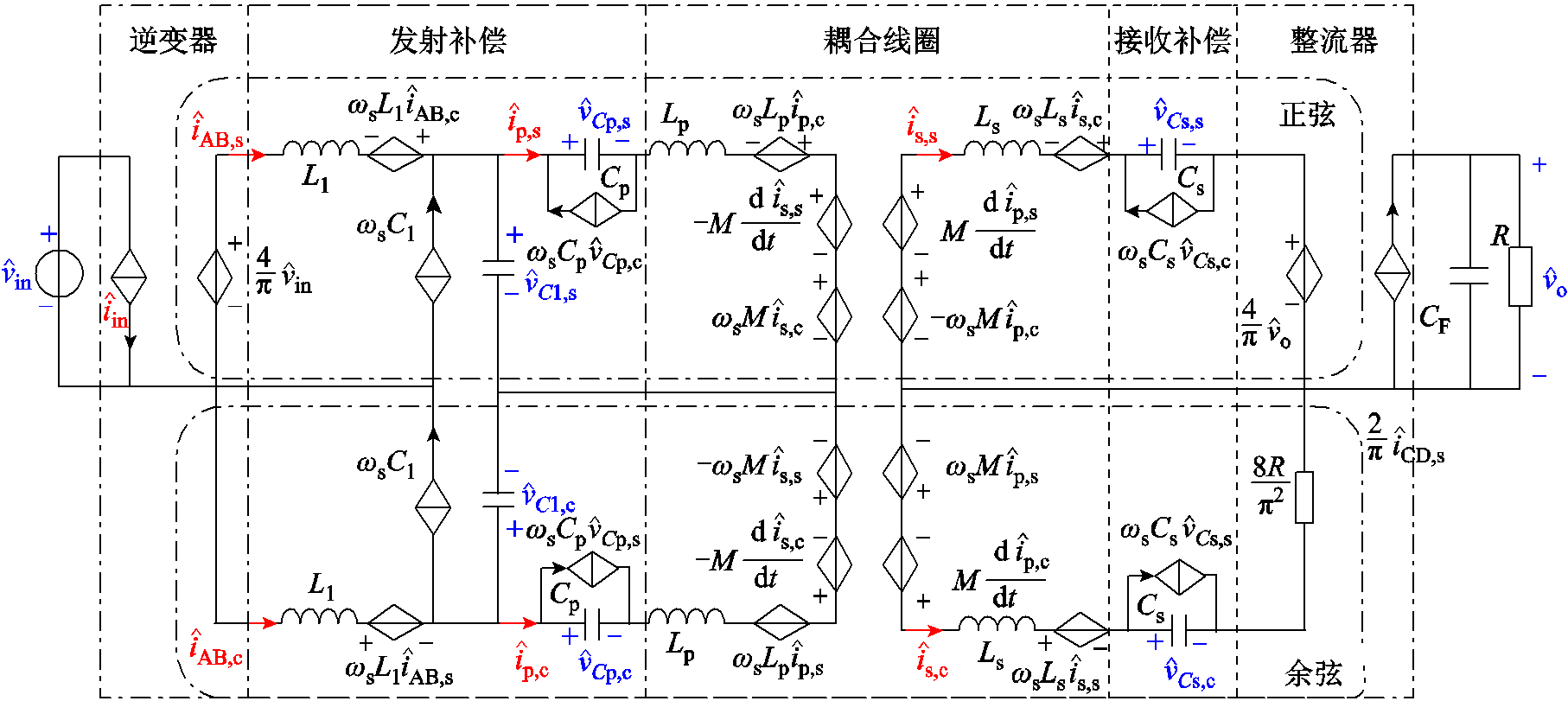
图6 LCC-S补偿的IPT系统的全阶小信号模型
Fig.6 Full-order model for IPT system use LCC-S compensation
LCC-S补偿的IPT系统中含有6个谐振元件，在系统的小信号模型中还需要将模型拆分为正余弦部分，这使得图6的谐振腔中包含12个谐振元件，最后导致该小信号模型的阶数为13阶。对于整流器与逆变器，已经不存在化简空间。因此，对于模型的降阶，重点在于谐振腔的化简。
图5中的小信号模型包含正弦和余弦分量，且含有耦合项，这使电路上的分析变得较为复杂。在稳态的交流系统中，可以用相量的实部与虚部分别表示正、余弦量。在此小信号模型中也可以利用相量来表示正弦与余弦量。将小信号中的正弦量与余弦量合并，即
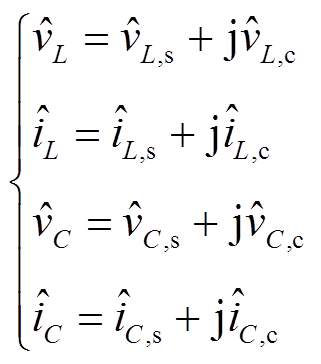（17）
式中，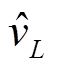
为复数，表示动态相量，其实数部分代表图5a中电压的正弦部分，虚数部分为图5a中电压的余弦部分；同理
、
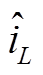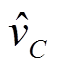和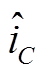
也有同样的性质。因此式（15）与式（16）可以分别改写为
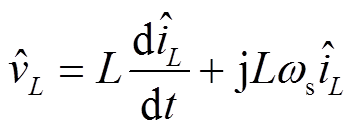（18）
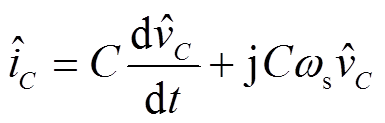（19）
根据式（18）和式（19），可以将电感电容的小信号模型转换为动态相量的形式，如图7所示。
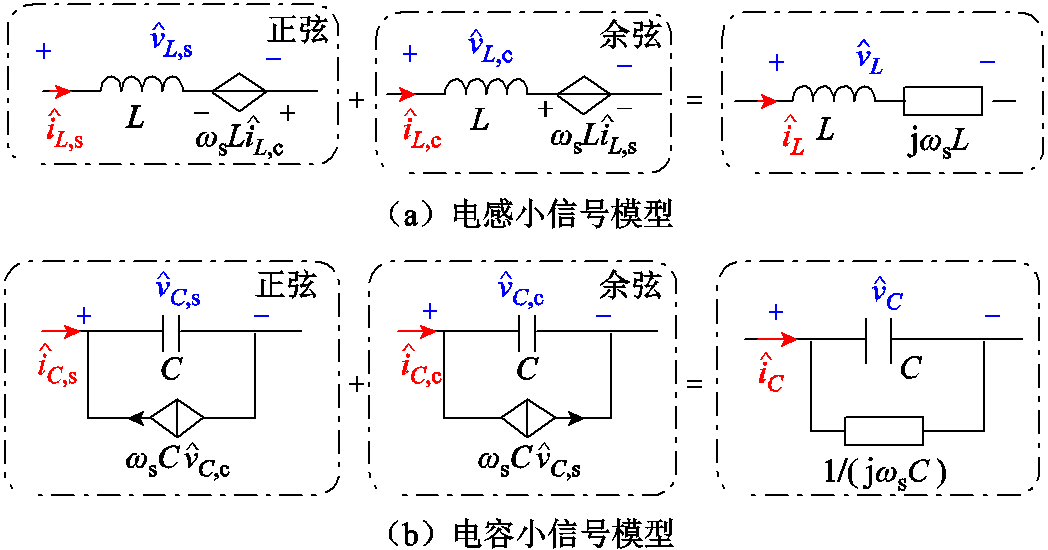
图7 EDF与动态相量法的转换
Fig.7 Transform between EDF and dynamic phasor model
通过这种方法可以得到谐振腔的小信号模型如图8所示。该模型与原模型是等价的。与原来的模型相比，该模型中不包含耦合项，有助于接下来的化简。
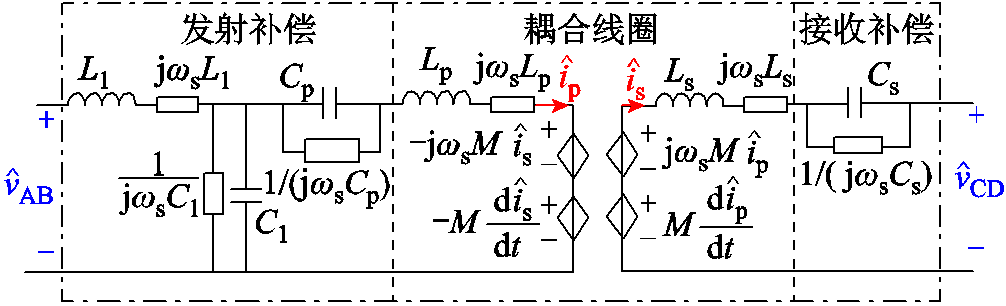
图8 谐振腔动态相量模型
Fig.8 Dynamic phasor model for resonant tank
值得一提的是，该等效模型仅适用于分析谐振腔内的小信号模型，若要获得系统完整的小信号模型，还需将电路分为正、余弦部分并与前端的整流电路和后端的逆变电路相连。因此虽然图8中仅含有6个谐振元件，其阶数依然为12阶。
文献[15]中对电容小信号模型进行化简，使得串联谐振变换器原来5阶的小信号模型降为3阶，这种方法可以应用于IPT系统中。
对于开关变换器，一般所关注的小信号频段在1/2开关频率以下。在所关注频段远低于开关频率，即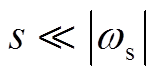
时，电容的小信号模型可以做如下近似。
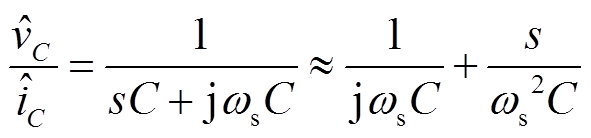（20）
则可以将电容的小信号模型化简为如图9所示的模型。
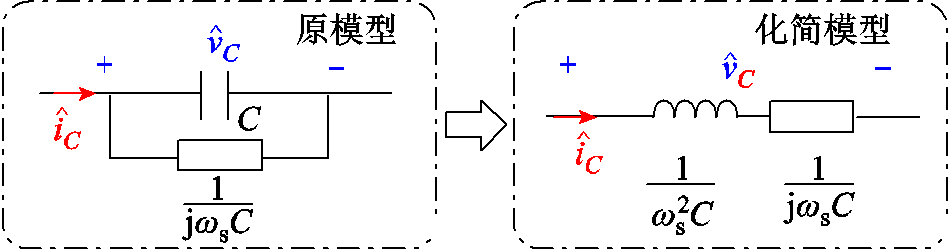
图9 电容小信号模型的化简
Fig.9 Simplification of the capacitor
LCC-S补偿的IPT中有3个电容，将其全部使用图9的方式化简，并与串联的电感合并，可得图10的模型。
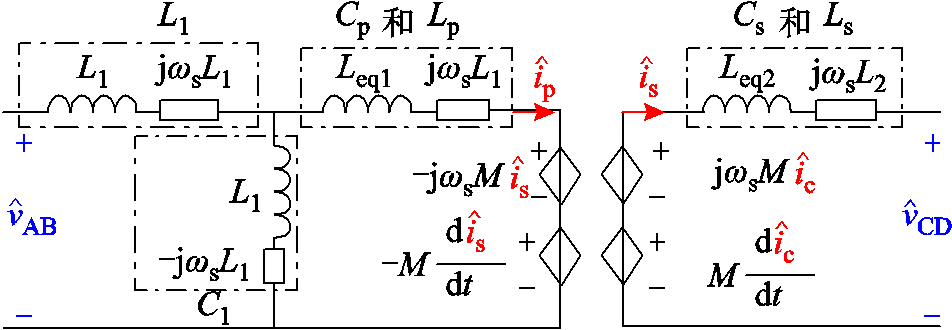
图10 基于式（20）化简后的谐振腔
Fig.10 Simplified circuit model for the resonant tank based on Equ.(20)
图10中，Leq与Xeq等参量在式（1）的频率条件下为
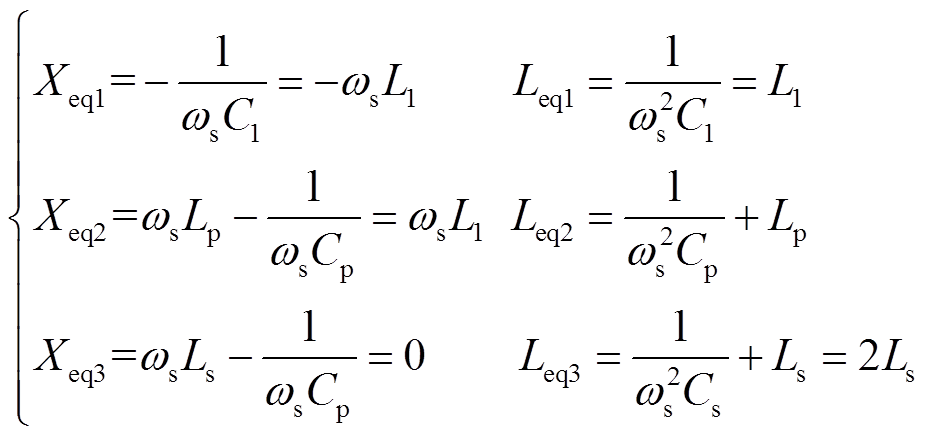（21）
在图10的化简电路中谐振元件大大减少，仅存在4个电感。发射端的L1、Leq1与Leq2三个等效电感及相连的等效阻抗jωsL1、jXeq1和jXeq2所组成的T型网络可以转换为受控源模型，如图11所示。
在图11所示的谐振腔的等效小信号模型中仅有3个谐振元件，并且可以发现该化简后的模型有很强的对称性。将该模型重新分解为正弦与余弦部分，并与整流器与逆变器相连，可以得到最终完整的小信号模型。
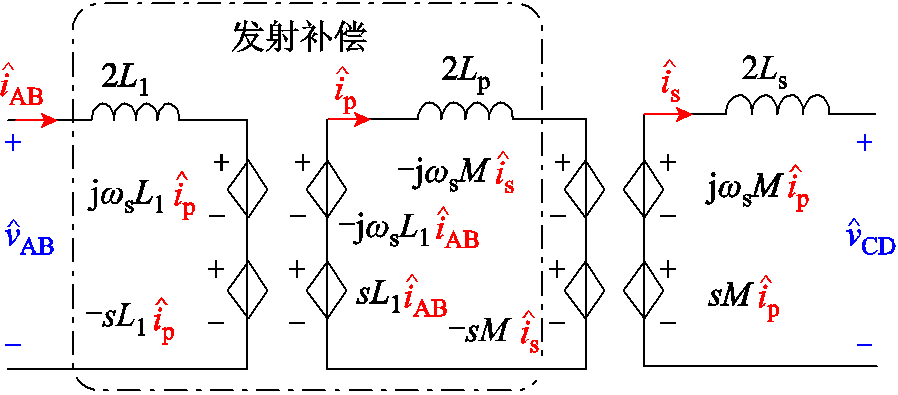
图11 谐振腔受控源模型
Fig.11 Induced voltage source model for resonant tank
最终化简后的小信号模型如图12所示。该模型的谐振腔内共含有6个谐振元件，加上整流器中的电容，最终阶数为7阶。相比原本13阶的系统，通过这种方法可以使得系统阶数大大降低。
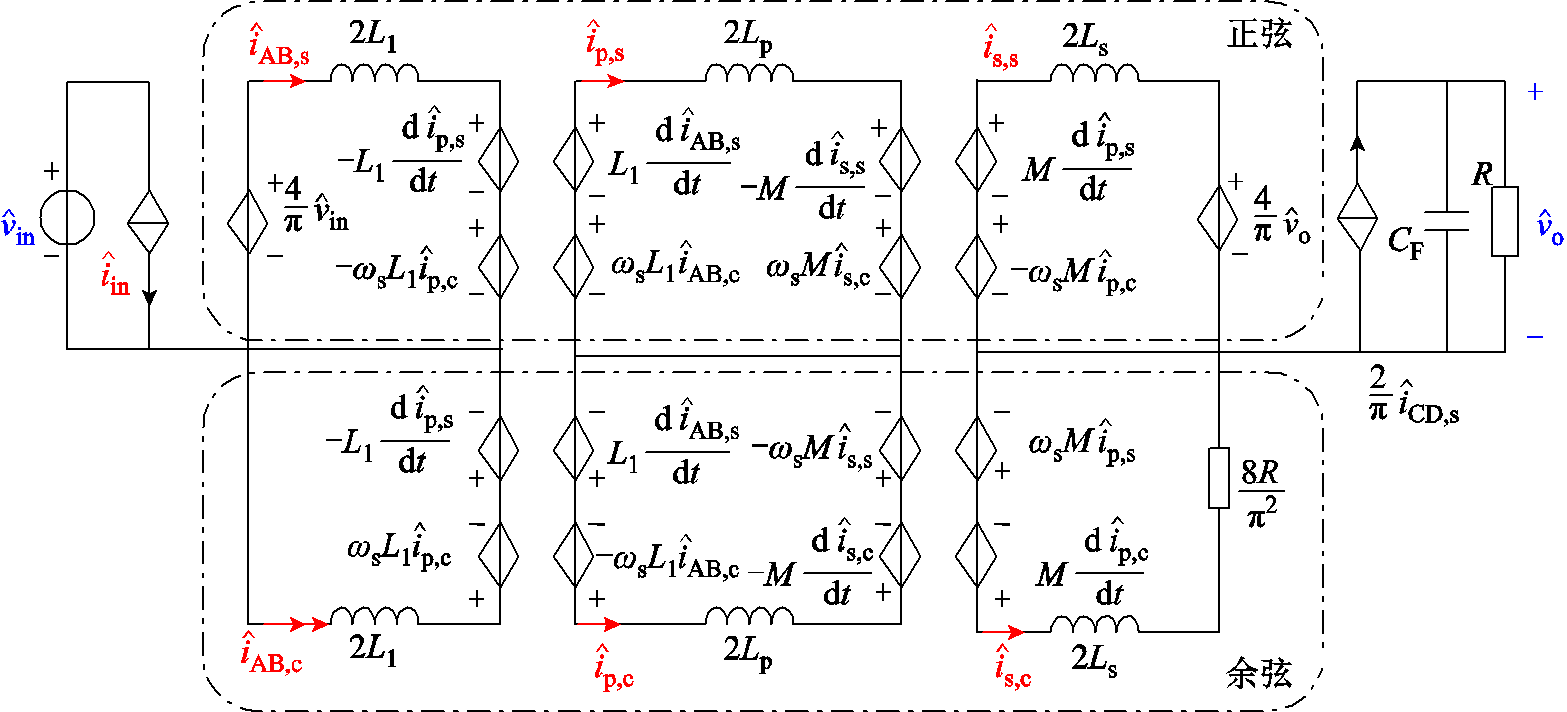
图12 降阶小信号模型
Fig.12 Reduced-order small-signal model
模型正确性将通过仿真与实验验证。小信号模型反映的是系统的动态特性，该动态特性可以利用不同频率下的交流增益表征。若不同频率下的响应仿真与模型均有较高的吻合度，则证明系统的模型准确。仿真软件采用SIMPLIS，该软件可以仿真不同频率下的小信号交流增益。该IPT系统使用全桥逆变器，IPT系统的参数见表1，其中CF为整流的滤波电容，k为线圈的耦合系数（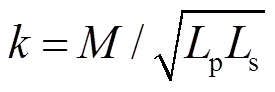
）。在图12中利用基尔霍夫电流定律与电压定律，可以计算出交流增益
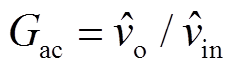的传递函数。模型计算与仿真的比较如图13所示，圆点实线代表仿真结果，三角虚线为模型计算结果。基于仿真与降阶模型的结果在1/5开关频率以下有较高的吻合度。
表1 仿真电路参数
Tab.1 Circuit parameter in the simulation
参数数值参数数值 L1/μH25C1/nF101.3 Lp/μH100Cp/nF33.8 Ls/μH100Cs/nF25.33 k0.2fs/kHz100 R/Ω20CF/μF10
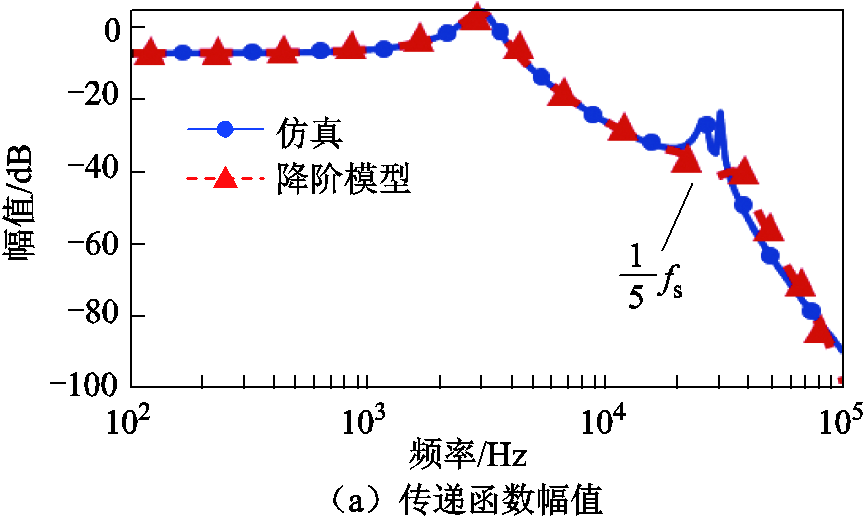
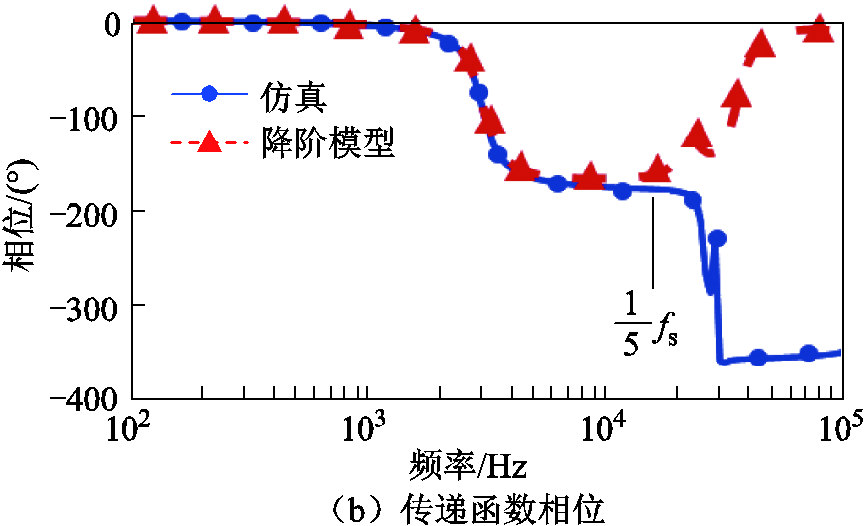
图13 仿真与模型的传递函数Gac比较
Fig.13 Transfer function Gac comparison between model-based calculations and simulation
为进一步验证模型准确性，本文建立了如图14所示的实验平台，该系统采用半桥逆变，其电路参数见表2。本次实验使用环路分析仪Bode100注入小信号。实验结果如图15所示。其中黑线表示实验所得数据，圆点实线表示仿真结果，三角虚线代表由降阶小信号模型所获得的传递函数。在1/5开关频率以下，模型计算与仿真实验结果吻合较好，这表明本文所提出的降阶小信号模型能很好地预测IPT系统真实的小信号特征。
图14 实验平台
Fig.14 Experimental platform
表2 实验电路参数
Tab.2 Circuit parameter in the experiment
参数数值参数数值 L1/μH24.9C1/nF101.5 Lp/μH117Cp/nF27.8 Ls/μH91Cs/nF28.33 k0.23fs/kHz100 R/Ω20CF/μF10
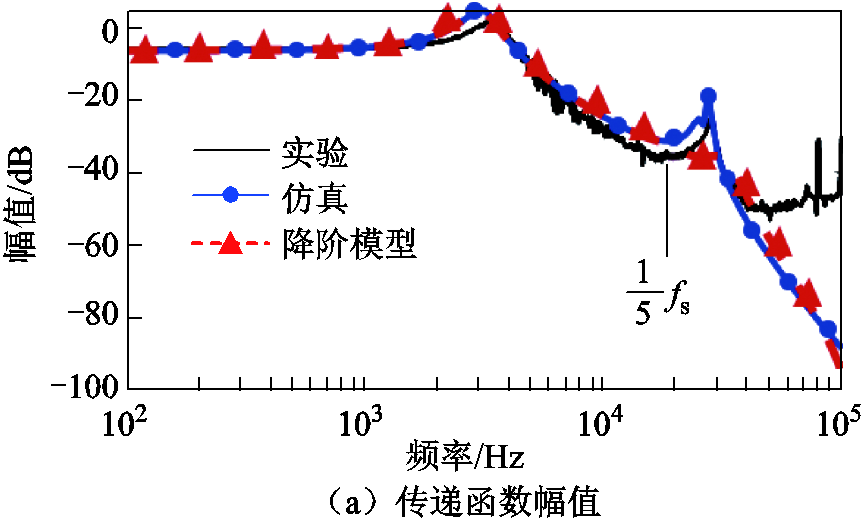
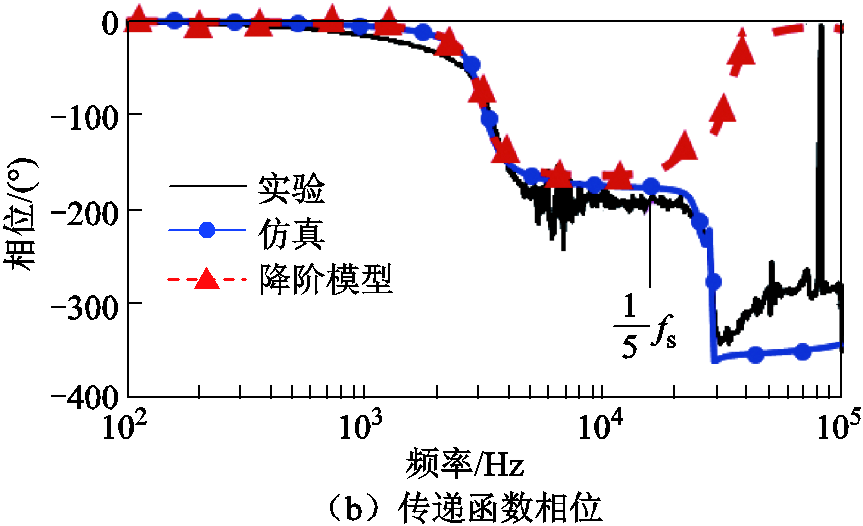
图15 仿真、实验与模型的传递函数Gac比较
Fig.15 Transfer function Gac comparison among model, simulation and experiment
本文以LCC-S补偿的IPT系统为例，探究IPT系统的建模与化简方法。通过扩展描述函数法，对电路中的各个部分进行建模，并获得电路各部分的等效电路模型，最终可以得到整个系统的小信号模型。等效电路模型具有很直观的物理含义。然后基于此等效电路，对系统进行降阶化简，使得原来13阶系统降至7阶。这种降阶方法具有通用性，可以运用于其他IPT系统中。
参考文献
[1] 李海娟, 黄学良, 陈中, 等. 含电动汽车无线充电的配电网可靠性评估[J]. 电工技术学报, 2015, 30(增刊1): 244-250.
Li Haijuan, Huang Xueliang, Chen Zhong, et al. Reliability evaluation of distribution network with wireless charging of electric vehicle[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 244-250.
[2] 赵争鸣, 刘方, 陈凯楠. 电动汽车无线充电技术研究综述[J]. 电工技术学报, 2016, 31(20): 30-40.
Zhao Zhengming, Liu Fang, Chen Kainan. New progress of wireless charging technology for electric vehicles[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 30-40.
[3] 曹玲玲, 陈乾宏, 任小永, 等. 电动汽车高效率无线充电技术的研究进展[J]. 电工技术学报, 2012, 27(8): 1-13.
Cao Lingling, Chen Qianhong, Ren Xiaoyong, et al. Review of the efficient wireless power transmission technique for electric vehicles[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 1-13.
[4] 黄学良, 谭林林, 陈中, 等. 无线电能传输技术研究与应用综述[J]. 电工技术学报, 2013, 28(10): 1-11.
Huang Xueliang, Tan Linlin, Chen Zhong, et al. Review and research progress on wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 1-11.
[5] 傅旻帆, 张统, 马澄斌, 等. 磁共振式无线电能传输的基础研究与前景展望[J]. 电工技术学报, 2015, 30(增刊1): 256-262.
Fu Minfan, Zhang Tong, Ma Chengbin, et al. Wireless power transfer using magnetic resonance coupling: basic considerations and practices[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 256-262.
[6] Zhang Zhen, Pang Hongliang, Georgiadis A, et al. Wireless power transfer—an overview[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1044-1058.
[7] Wang C S, Covic G A, Stielau O H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J]. IEEE Transactions on Industrial Electronics, 2004, 51(1): 148-157.
[8] He Rong, Zhao Peng, Fu Minfan, et al. Decomposition and synthesis of high-order compensated inductive power transfer systems for improved output controllability[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(11): 4514-4523.
[9] Zhao Peng, Zheng Guangce, He Rong, et al. A 45-W two-stage wireless fast charger using unregulated inductive power transfer[J]. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 2021, 2(3): 287-296.
[10] Wester G W, Middlebrook R D. Low-frequency characterization of switched DC-DC converters[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(3): 376-385.
[11] Yang E X, Lee F C, Jovanovic M M. Small-signal modeling of series and parallel resonant converters[C]//Seventh Annual Applied Power Electronics Conference and Exposition, Boston, MA, USA, 1992: 785-792.
[12] Zahid Z U, Dalala Z M, Zheng Cong, et al. Modeling and control of series–series compensated inductive power transfer system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(1): 111-123.
[13] Feng Hao, Lukic S M. Reduced-order modeling and design of single-stage LCL compensated IPT system for low voltage vehicle charging applications[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 3728-3739.
[14] Deng Qijun, Wang Ziyi, Chen Cheng, et al. Modeling and control of inductive power transfer system supplied by multiphase phase-controlled inverter[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 9303-9315.
[15] Tian Shuilin, Lee F C, Li Qiang. A simplified equivalent circuit model of series resonant converter[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3922-3931.
Small-Signal Model for Inductive Power Transfer Systems Using LCC-S Compensation
Abstract An inductive power transfer (IPT) system requires a feedback controller to stabilize the output, which highly depends on an accurate small-signal model. In the past years, the extended describing function (EDF) is widely used to address the modeling issue for resonant converters. However, the high-order resonant tank of IPT would lead to a complicated model if EDF is directly applied. In order to simplify the model, this paper explored a circuit-based method to reduce the order for both series and parallel resonant circuits. An example LCC-C compensated system was used to explain the concept. This general simplification can be extended to any other high-order IPT systems.
keywords：Inductive power transfer, equivalent circuit model, extended describing function, reduced-order model
DOI:10.19595/j.cnki.1000-6753.tces.211263
中图分类号：TM46
收稿日期 2021-08-12
改稿日期 2021-11-11
郑广策 男，1997年生，博士研究生，研究方向为无线电能传输。E-mail：zhenggc@shanghaitech.edu.cn
傅旻帆 男，1987年生，教授，博士生导师，研究方向为无线电能传输、高频磁集成、超高频变换器、谐振变换器的建模与控制及宽禁带器件的应用等。E-mail：fumf@shanghaitech.edu.cn（通信作者）
（编辑 李冰）