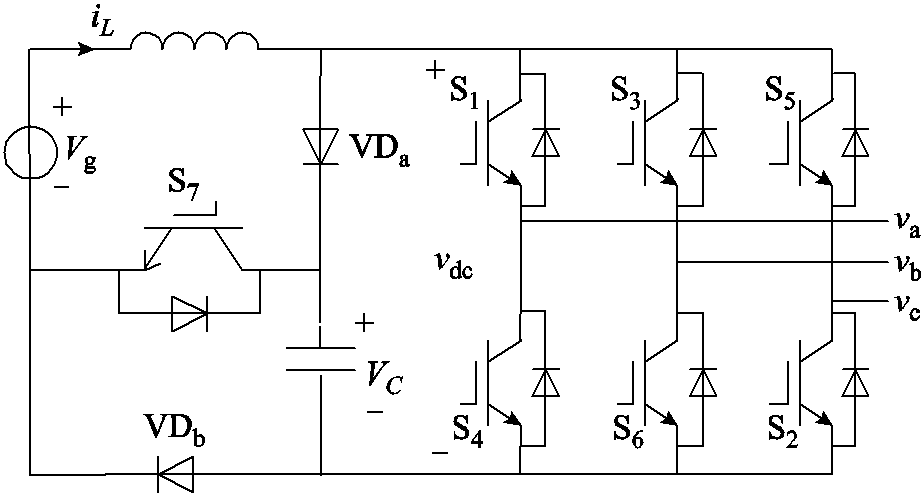
图1 三相qSBI
Fig.1 Three-phase qSBI
摘要 高频电流纹波影响了变换器电感体积和质量,针对准开关升压逆变器,传统的直通调制算法并不能做到电感电流纹波最小。该文提出一种最小电感电流纹波的空间矢量调制方法,重新分配了开关管导通与关断时序。在此基础上,推导使得电感电流纹波最小时直通占空比和导通占空比所满足的数学关系。最后,通过仿真和实验对比了所提出的新型调制算法和传统算法在抑制电感电流纹波方面的性能,结果证明了理论分析的正确性。
关键词:准开关升压逆变器 电流纹波 直通 空间矢量调制
近年来,Z源/准Z源逆变器(Z Source Inverter/quasi Z Source Inverter, ZSI/qZSI)因其良好的直通可靠性和宽电压调节范围,受到越来越多学者的重视[1-6]。Z源网络由两个电感、两个电容和一个二极管组成,与DC-DC网络相比,节省了有源开关器件[7-9]。通过直通状态和非直通状态的切换,完成对电感和电容的充放电控制,提高了直流链电压[10]。三相Z源变换器作为近年来的研究热点,在电机调速、光伏发电、电动汽车等诸多领域得到了广泛的应用[11-13]。
传统Z源网络中的电感和电容使系统的质量和体积增加,大大降低了变换器的功率密度。为了解决这个问题,有学者提出了一种基于传统ZSI/qZSI的准开关升压逆变器(quasi Switched Boost Inverter, qSBI)[14-16]。如图1所示,qSBI的阻抗网络中仅有一个电容和一个电感,但增加了一个开关管S7。S7在直通状态下导通,在非直通状态下关断。qSBI相比ZSI/qZSI具有更低的开关器件电流应力和更强的升压能力,该变换器可以通过级联更多的单元获得更高的升压比,但牺牲了变换器的体积、重量和成本。M. K. Nguyen等探索了一系列PWM控制策略来解决这个问题[17-19]。与传统的PWM方法相比,这些策略引进了一种新的工作状态,即开关S7在非直通状态下导通工作,大大提升了三相qSBI的升压能力。然而,在此系列控制方法下,电感电流纹波并未得到优化,且开关频率也有所提高。众所周知,电感的体积受电感电流纹波的影响。大的电流纹波情况下,为了防止铁心饱和,往往需要增大电感体积。

图1 三相qSBI
Fig.1 Three-phase qSBI
本文提出了一种最小电感电流纹波的Z源空间矢量调制(minimum Z-source Space Vector Modulation, ZSVMm)方法。后续研究证明,电感电流纹波最小时,S7导通时间与直通时间之间需要满足某种数学关系。本文提出了一种新型调制算法,并在分析变换器工作模态的基础上,探索了使得电感电流纹波最小的数学关系。仿真和实验结果验证了所提出的ZSVMm调制策略理论分析的正确性。
qSBI的等效电路如图2所示。
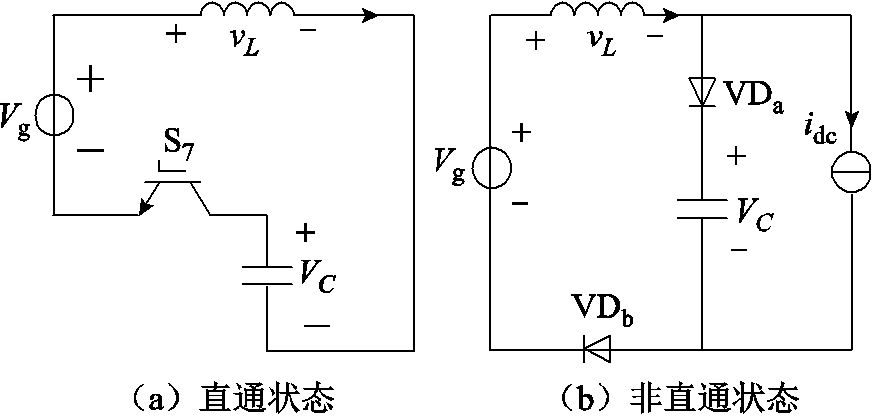
图2 qSBI的等效电路
Fig.2 Equivalent circuits of the qSBI
当同一桥臂的上、下两个开关管同时导通时,逆变器工作在直通状态,此时S7也导通,如图2a所示。在非直通状态下,qSBI相当于电压源逆变器,此时S7关断,如图2b所示。
根据伏秒平衡原理得到
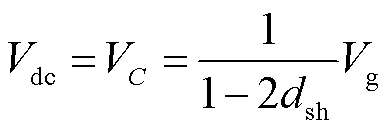 (1)
(1)
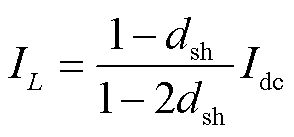 (2)
(2)
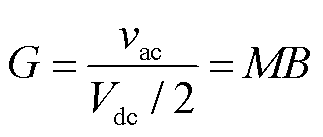 (3)
(3)
式中,Vdc、VC和Vg分别为直流链电压峰值、电容电压和直流输入电压;dsh为直通占空比,即直通时间在一个开关周期中的占比,dsh=Tsh/Ts,Ts为开关周期,Tsh为直通时间;IL为电感电流;Idc为等效逆变侧电流;M为调制比;B为升压比,B=1/(1-2dsh);vac为交流相电压峰值。
空间矢量脉宽调制(Space Vector Pulse Width Modulatiom, SVPWM)算法将空间划分为六个扇区。对于第一扇区,时间间隔可以表示为[20]
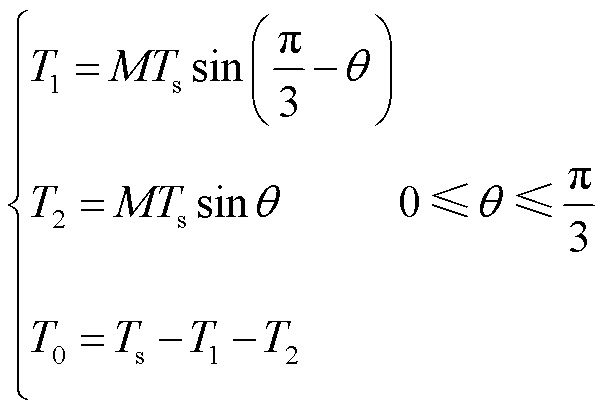 (4)
(4)
式中,θ为参考电压的空间矢量角;T0为零矢量的作用时间;T1和T2为第一扇区中相邻基本有效矢量的作用时间。
基于qSBI的传统Z源空间矢量调制(Z-source Space Vector Modulation, ZSVM)与ZSI/qZSI的相同[21],它将直通状态分成四个相等的分段,分别插入传统零矢量和有效矢量之间,且不增加开关频率,如图3a所示。S7在直通状态下导通,在非直通状态下关断。
本文提出的最小电感电流纹波的ZSVMm调制法如图3b所示。
该调制策略在不增加开关频率的情况下,将直通状态分成四个相等的部分,分别插入到有效矢量开始或结束处。S7在部分非直通状态下导通,在其他状态下关断。值得注意的是,S7的控制方法不同于传统方法,使得三相qSBI获得两种新的工作模态。
在所提出的新型调制算法下,变换器的直通状态子电路如图4a所示,其中S7关断,此时电感电压和电容电流为
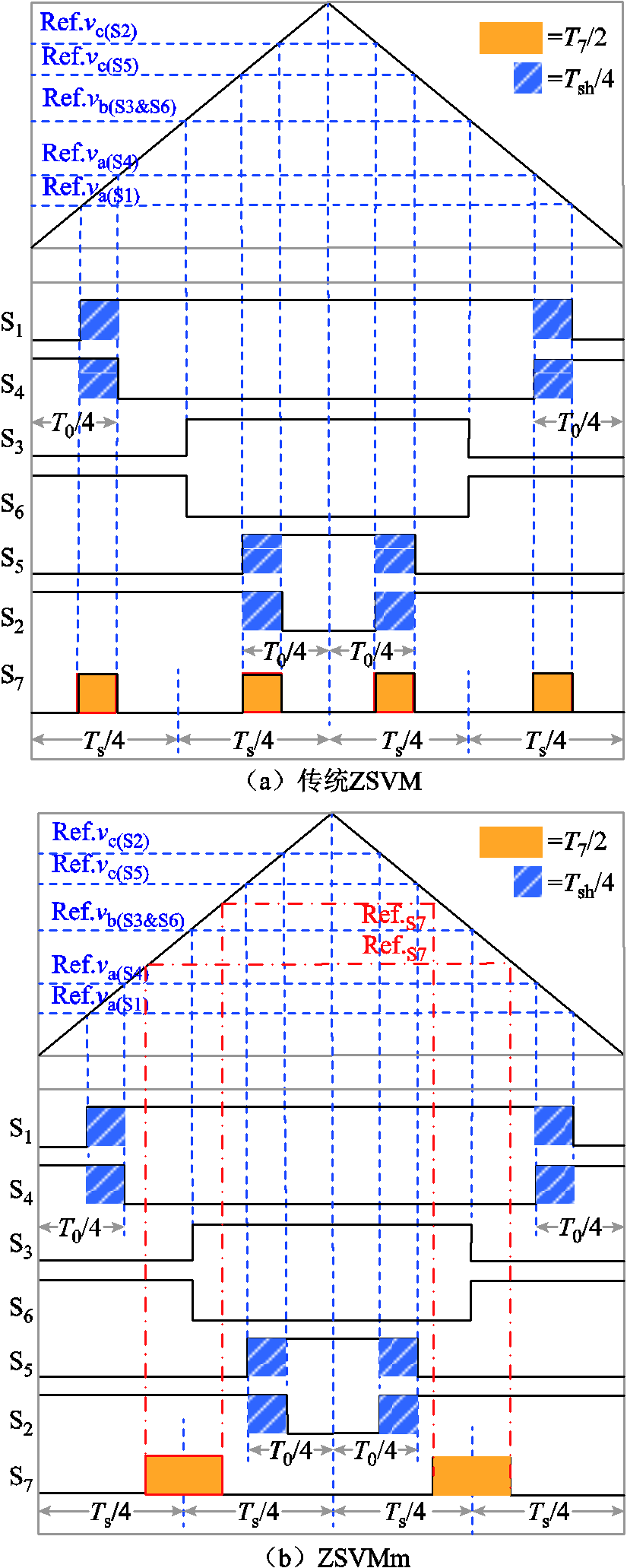
图3 开关切换时序
Fig.3 Switching sequence
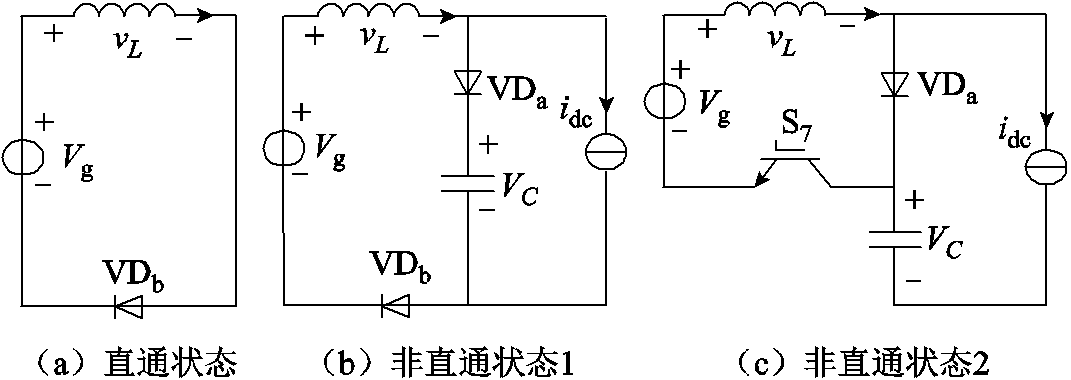
图4 qSBI的工作模态
Fig.4 Working states of the qSBI
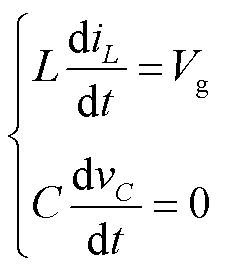 (5)
(5)
式中,L和C分别为阻抗网络中的电感值和电容值;iL为电感电流;vC为电容电压。
非直通状态1如图4b所示,该状态下S7仍然关断,此时的电感电压和电容电流可以表示为
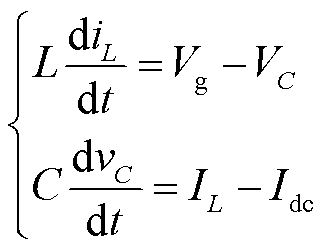 (6)
(6)
非直通状态2如图4c所示,该状态下S7导通,电感电压和电容电流可表示为
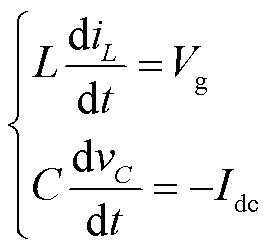 (7)
(7)
对式(5)~式(7)采用电感伏秒平衡原理和电容安秒平衡原理,可以得到
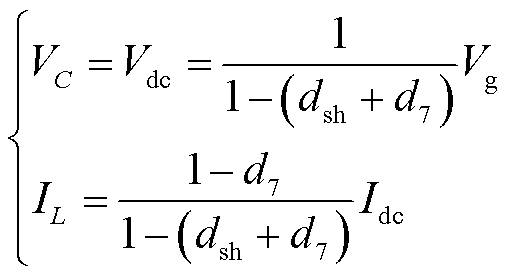 (8)
(8)
式中,d7为S7导通占空比,即S7导通时间与开关周期的比值,d7=T7/Ts;T7为S7导通时间。
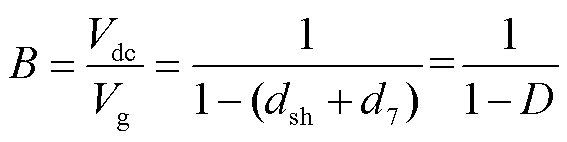 (9)
(9)
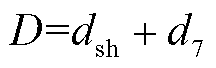 (10)
(10)
式中,D为升压占空比。传统ZSVM可以看成是d7=dsh时的一种特殊情况,即满足D=2dsh。
如式(10)所示,升压占空比D是直通占空比dsh和S7导通占空比d7之和,这意味着同一升压占空比可以由无数组不同的dsh和d7组合得到。通过分析发现,存在一种最小电感电流纹波的最佳分配方案。关于dsh、d7和D的函数表达式的理论分析如下。
在非直通状态1下,qSBI阻抗网络中的电感放电,电感电压vL为负(见图4b),即
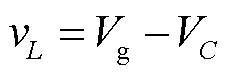 (11)
(11)
在直通状态和非直通状态2下,qSBI阻抗网络中电感充电,电感电压vL为正,其数值等于直流电源电压,如图4a和图4c所示。
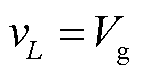 (12)
(12)
在半个开关周期中,ZSVMm调制下qSBI的直流链电压和电感电流纹波如图5所示。
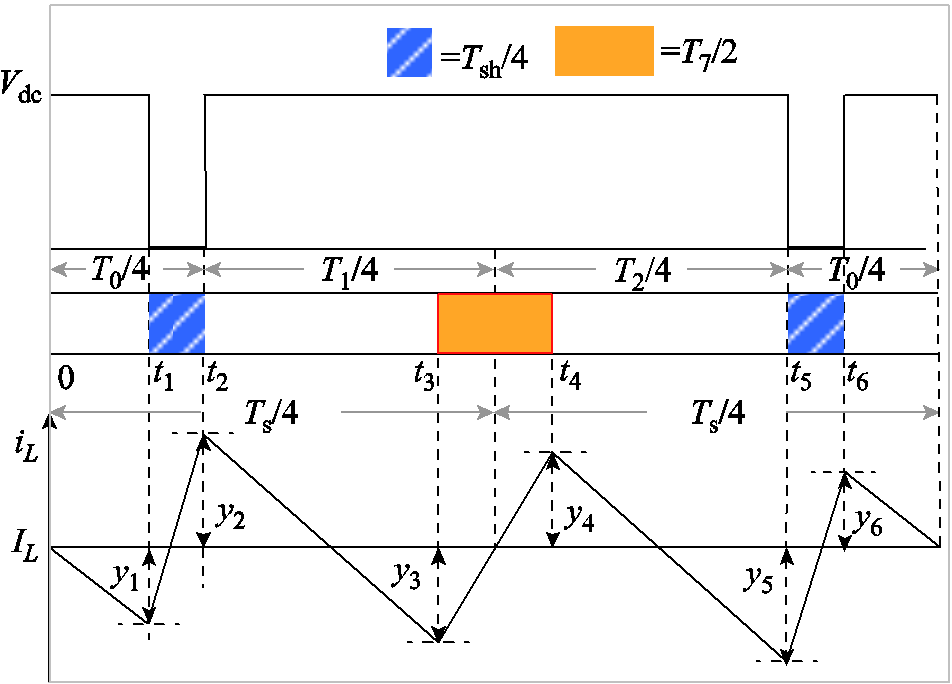
图5 直流链电压和电感电流纹波
Fig.5 Inductor current ripple in half modulation cycle
电感电流纹波的瞬时值为yx(x=1,2,×××,6),具体描述为
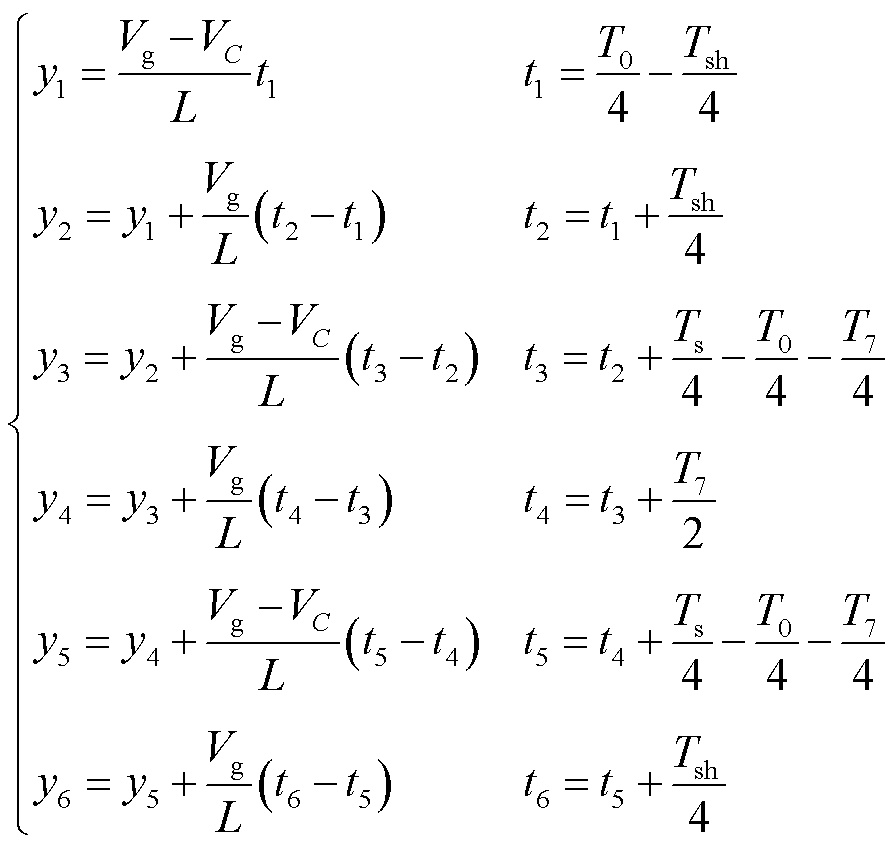 (13)
(13)
根据电感电流波形的对称性,|y1|=|y6|,|y2|=|y5|和|y3|=|y4|。将式(4)与式(9)、式(10)代入到式(13)得到
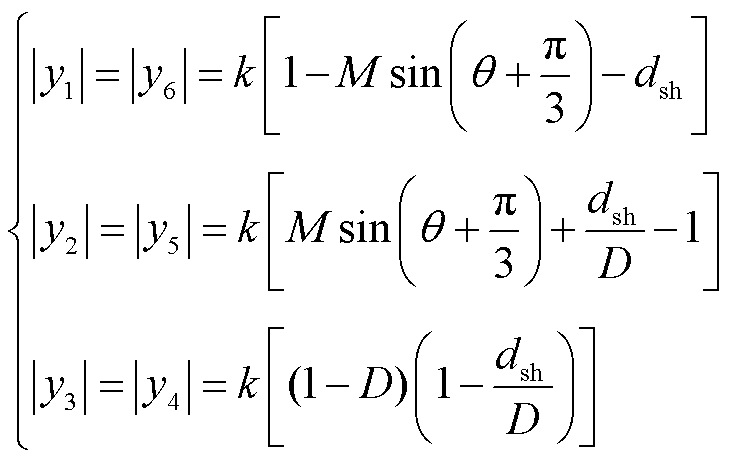 (14)
(14)
式中, 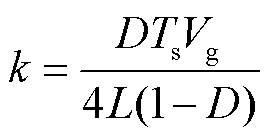 。
。
当θ=0°(或θ=π/3)和θ=π/6时,|y1|和|y2|分别达到最大值。电感电流纹波的最大值|yx|max(x=1,2,×××, 6)的表达式为
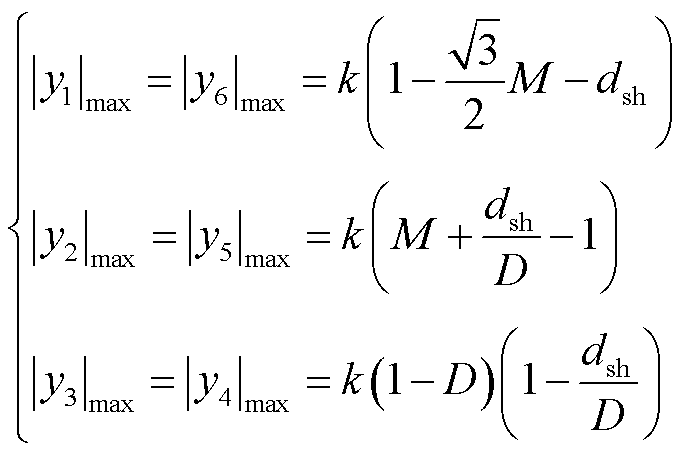 (15)
(15)
电感电流纹波的峰-峰值为
 (16)
(16)
通过式(15)容易得到不等式|y2|max>|y1|max和|y3|max>|y1|max,这意味着一个开关周期内的最大电感电流纹波为|y2|max或|y3|max。为了获得最小的电感电流纹波,必须满足|y2|max =|y3|max,从而得到
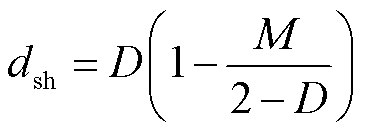 (17)
(17)
同时,还应满足
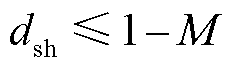 (18)
(18)
将式(17)代入式(10),得到d7的表达式为
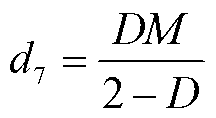 (19)
(19)
因此,使得电感电流纹波最小的完整条件为
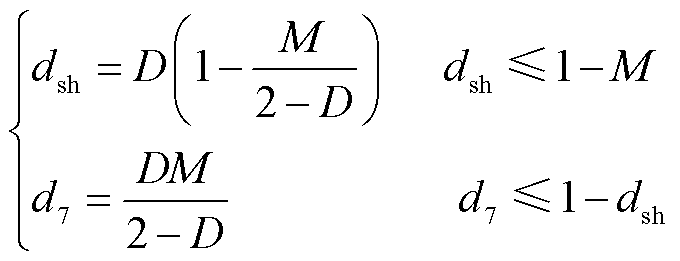 (20)
(20)
ZSVMm调制策略下的最大电感电流纹波为
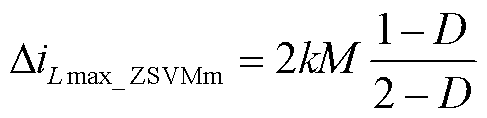 (21)
(21)
传统ZSVM下的电感电流纹波如图6所示。
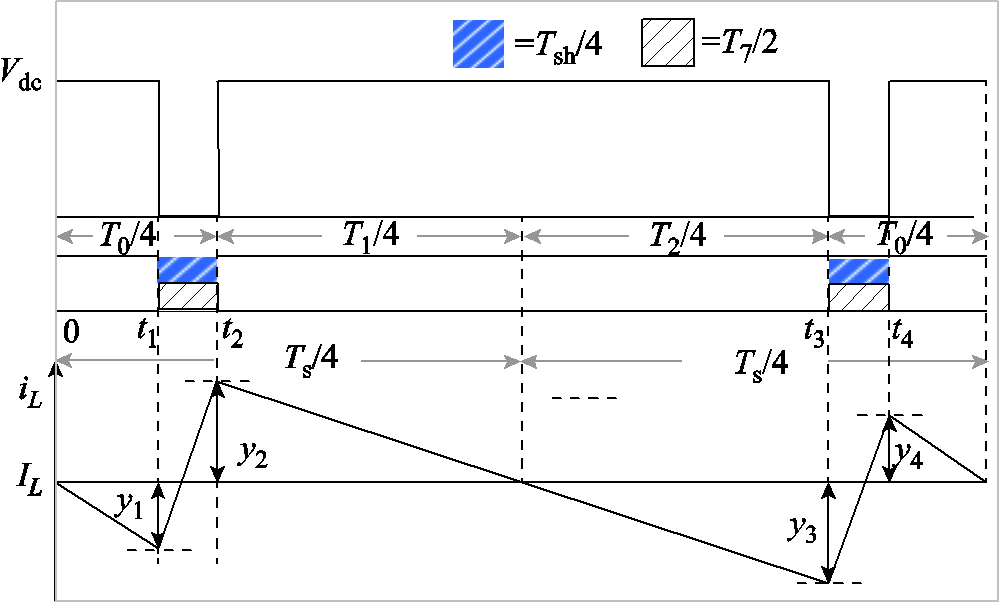
图6 传统ZSVM的电感电流纹波
Fig.6 Inductor current ripple of the traditional ZSVM
最大电感电流纹波可以表示为[22]
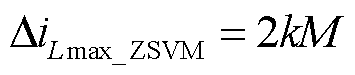 (22)
(22)
第一扇区中,传统ZSVM和新型ZSVMm的电感电流纹波分布如图7所示,其中在θ=30°时可以观察到最大值,在空间矢量角越靠近0°和60°的位置,其纹波幅值越小。

图7 第一扇区的电感电流纹波分布
Fig.7 Inductor current ripple in the first sector
在两种不同调制方法下,最大电感电流纹波随调制比M和升压占空比D的变化情况如图8所示,可以看到,两种调制的电感电流纹波均随着调制比和升压占空比的增大而增大。

图8 最大电感电流纹波分布
Fig.8 The maximum inductor current ripple
根据式(21)和式(22)的推导结果,两种调制方法下最大电感电流纹波比值可以表示为
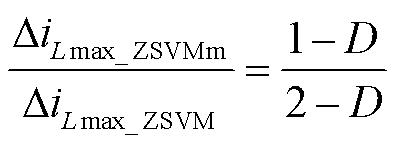 (23)
(23)
电感电流纹波比值随升压占空比D的变化规律如图9所示。
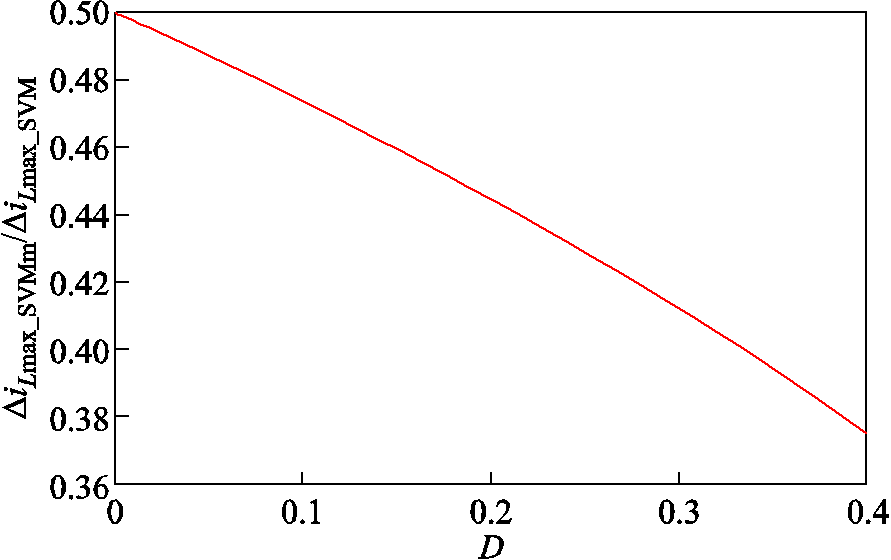
图9 不同调制方法下电感电流纹波比值
Fig.9 Inductor current ripple ratio with different modulation methods
可以看出,相同的调制比下,ZSVMm的电感电流纹波最大值比传统ZSVM的减小了一半以上,随着升压占空比的增大,ZSVMm在降低电感电流纹波方面的优势越发明显。
本节对传统ZSVM调制策略和所提出的最小电感电流纹波的ZSVMm调制法分别进行了仿真和实验验证。其中,系统中各部分的参数见表1。
表1 仿真和实验参数
Tab.1 Simulation and experiment parameters

参数数值 电压Vg/V100 开关频率f/ kHz10 qSBI电感L/μH320 qSBI电容C/μF440 负载电阻Rload/Ω10 负载电感Lload/mH1.15
图10和图11给出了ZSVM和ZSVMm控制时,不同升压占空比下直流链电压和电感电流纹波的仿真波形。
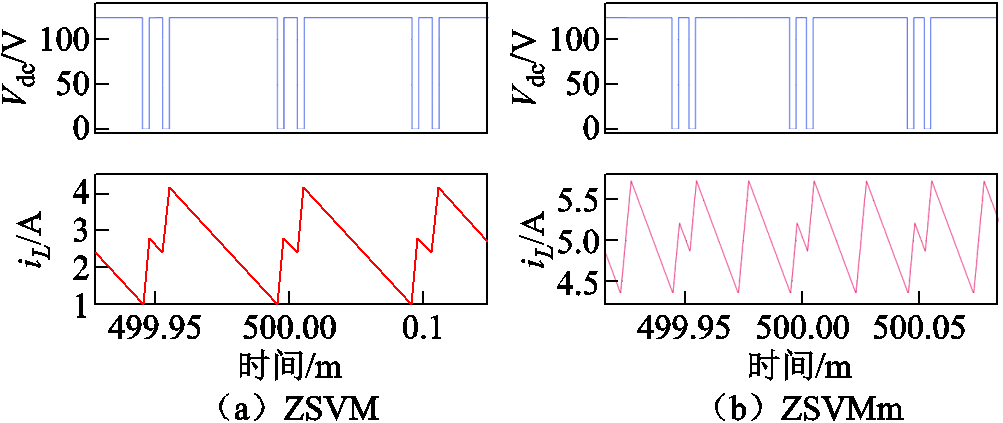
图10 D=0.2时直流链电压和电感电流的仿真波形
Fig.10 Simulation results of DC-link voltage and inductor current when D=0.2
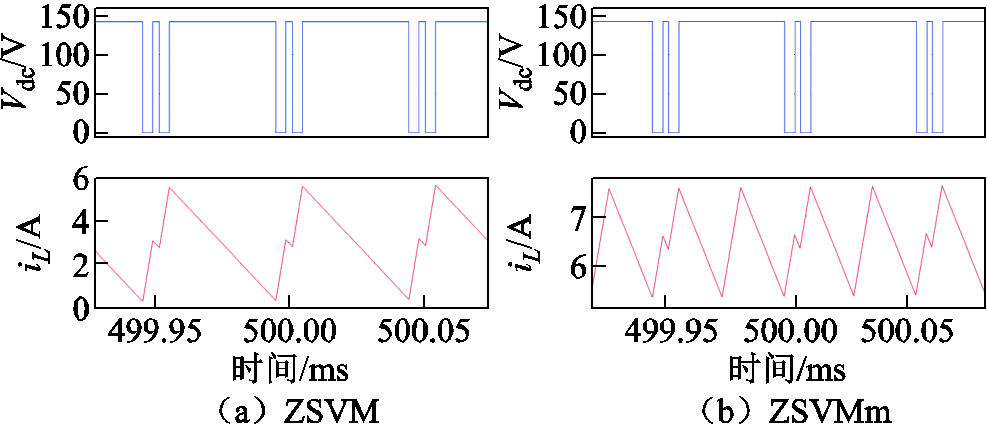
图11 D=0.3时直流链电压和电感电流的仿真波形
Fig.11 Simulation results of DC-link voltage and inductor current when D=0.3
对于这两种方案,最大电感电流纹波均出现在每个扇区中间的θ=30°处。
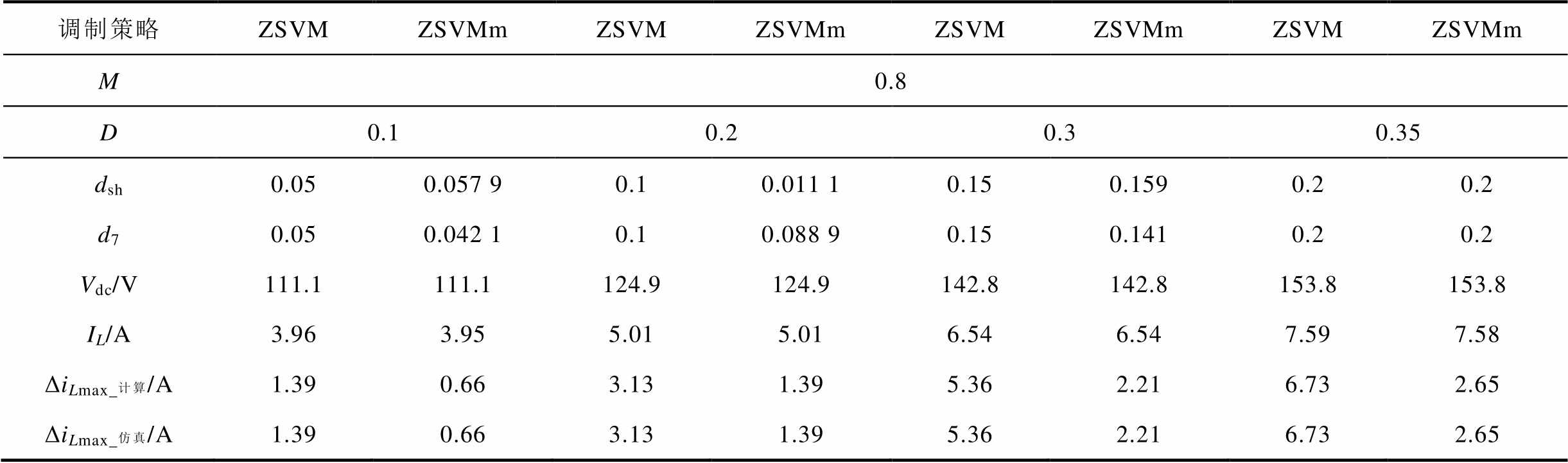
仿真测得的其他升压占空比下的电感电流纹波大小见表2。对于两种方案,最大电感电流纹波均随着升压占空比的增加而增加,在相同升压占空比下,ZSVMm控制的电感电流纹波始终小于传统ZSVM控制,这与理论分析相一致。
表2 仿真结果
Tab.2 Simulation results
调制策略ZSVMZSVMmZSVMZSVMmZSVMZSVMmZSVMZSVMm M0.8 D0.10.20.30.35 dsh0.050.057 90.10.011 10.150.1590.20.2 d70.050.042 10.10.088 90.150.1410.20.2 Vdc/V111.1111.1124.9124.9142.8142.8153.8153.8 IL/A3.963.955.015.016.546.547.597.58 ΔiLmax_计算/A1.390.663.131.395.362.216.732.65 ΔiLmax_仿真/A1.390.663.131.395.362.216.732.65
为了进一步验证ZSVMm调制法的有效性,搭建了如图12所示的实验平台,包括TMS320F28335数字信号处理器、IGBT Concept双驱动模块、qSBI网络、三相IGBT逆变桥和三相阻感负载等。

图12 三相qSBI实验平台
Fig.12 Three-phase qSBI experiment platform
图13a、图13b和图14a、图14b分别自上而下显示了ZSVM和ZSVMm在工频周期内的实验波形,包括电容电压VC、直流电源电压Vg、负载交流相电流iac和相电压vac。
可以看到,传统ZSVM和本文提出的ZSVMm在输入电压Vg相同的情况下,电容电压VC相同,输出电压和电流正弦度良好,周期为50Hz,说明两种调制方式升压能力是相同的。图13c、图13d和图14c、图14d分别给出了ZSVM和ZSVMm在开关周期内的直流链电压Vdc和电感电流iL纹波的实验波形,在θ=30°处测得最大电感电流纹波。从图中可以看出,与传统ZSVM相比,新提出的ZSVMm方法在电感电流纹波方面明显减小。
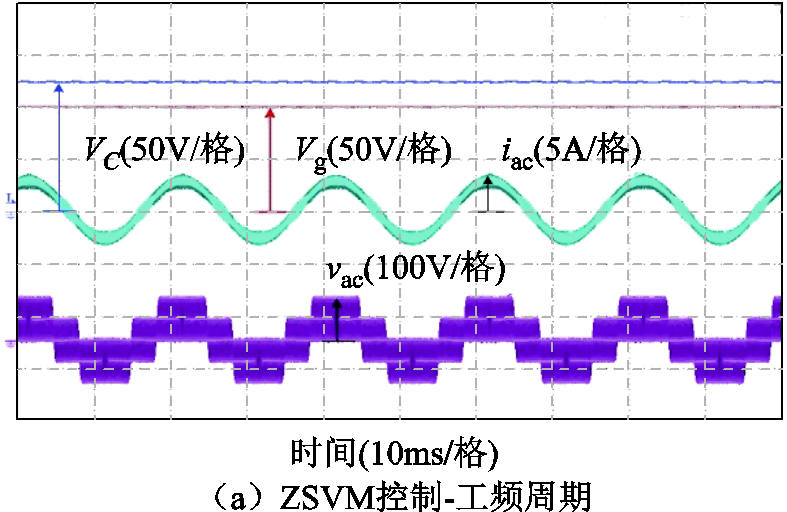
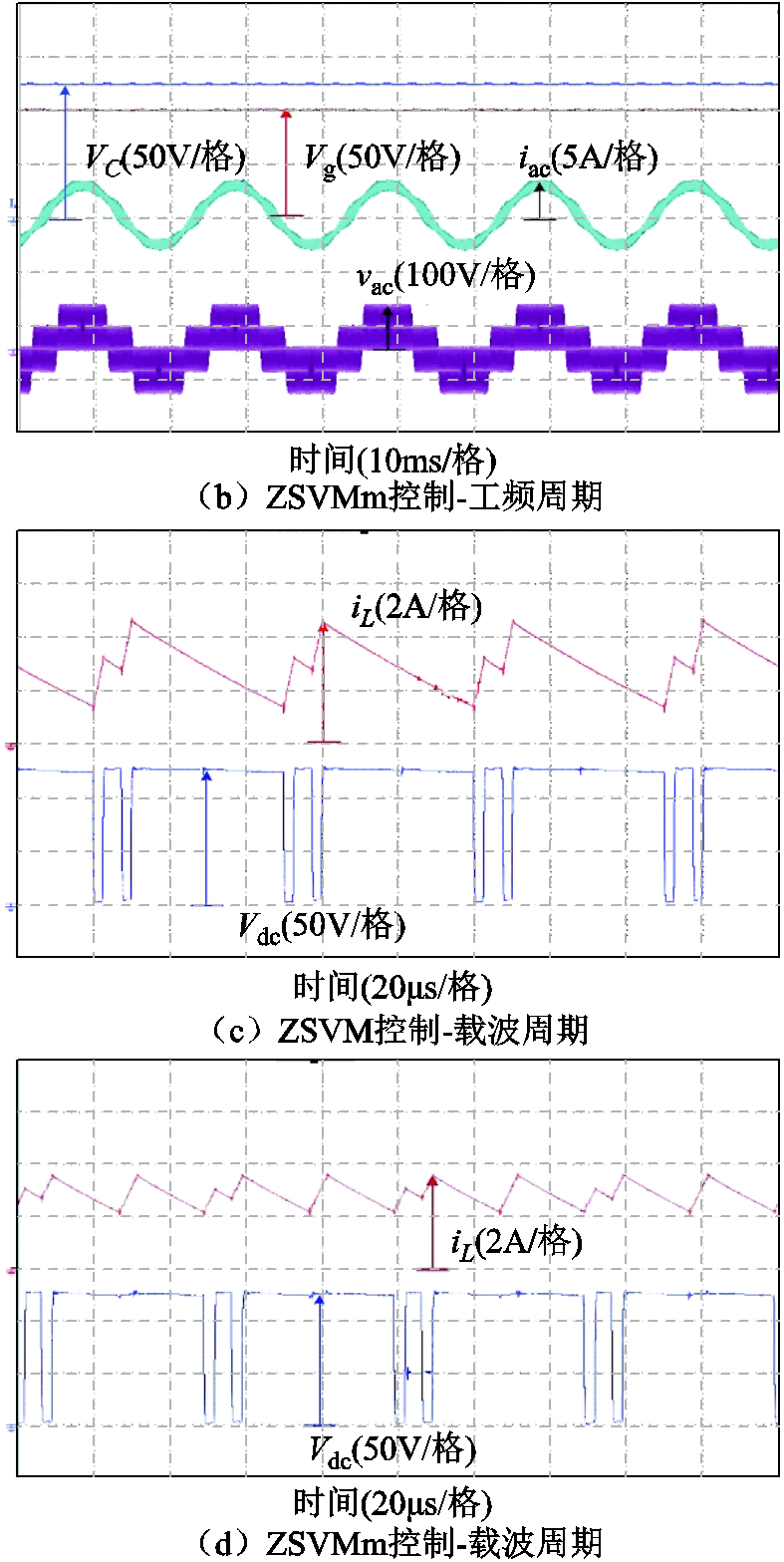
图13 D=0.2时工频和开关周期下的实验波形
Fig.13 Experimental waveforms in line and switching period when D=0.2
实验还测试了另外两组典型升压占空比下的电感电流纹波数据,结果见表3。
表3 实验结果
Tab. 3 Experimental results
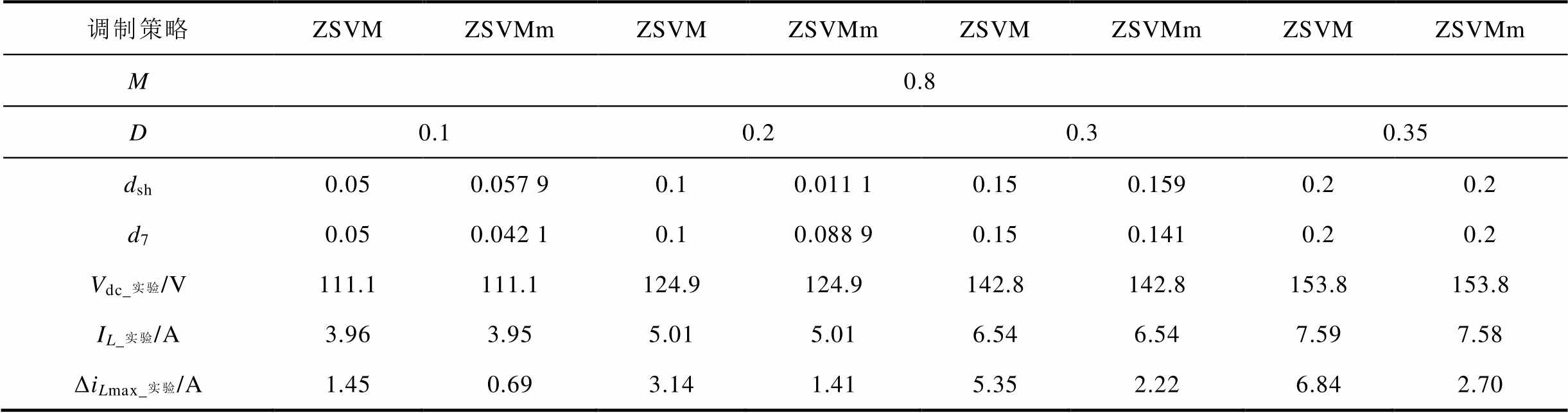
调制策略ZSVMZSVMmZSVMZSVMmZSVMZSVMmZSVMZSVMm M0.8 D0.10.20.30.35 dsh0.050.057 90.10.011 10.150.1590.20.2 d70.050.042 10.10.088 90.150.1410.20.2 Vdc_实验/V111.1111.1124.9124.9142.8142.8153.8153.8 IL_实验/A3.963.955.015.016.546.547.597.58 ΔiLmax_实验/A1.450.693.141.415.352.226.842.70

图14 D=0.3时工频和开关周期下的实验波形
Fig.14 Experimental waveforms in line and switching period when D=0.3
图15给出了不同升压占空比下,应用两种调制策略所得到的电感电流纹波。从图15中可以看出,ZSVMm控制的电感电流纹波始终小于传统ZSVM控制,且占空比越大,优势越明显,仿真和实验结果相一致。
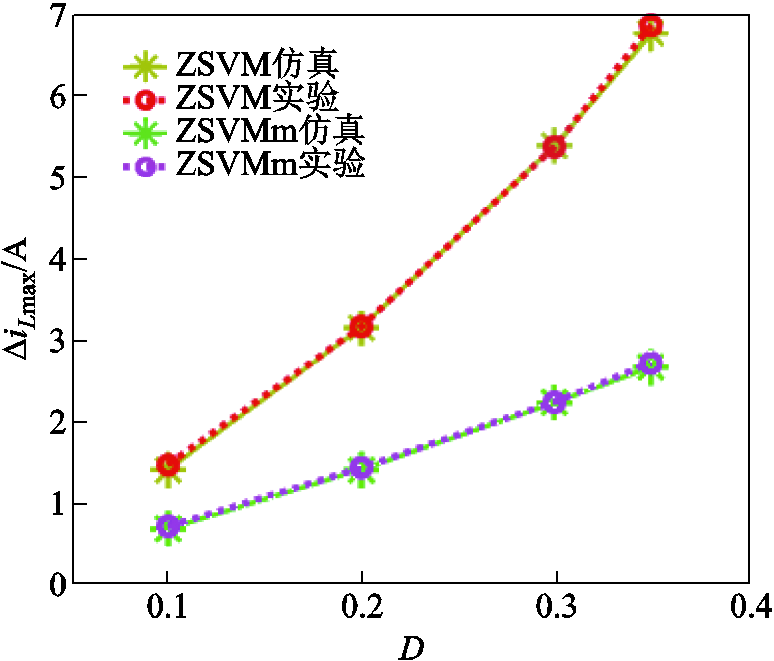
图15 仿真和实验结果对比图
Fig.15 Results of simulation and experiment with the ZSVM and ZSVMm methods
本文提出了一种最小电感电流纹波的空间矢量调制方法,在不增加开关频率的情况下,将直通状态分成四个相等的部分,分别插入到有效矢量开始或结束处。将第七开关管S7切换时序重新分配,在部分非直通状态下导通,在其他状态下关断。推导了直通占空比和导通占空比所满足的数学关系,使得电感高频电流纹波最小。与传统ZSVM调制相比,ZSVMm调制下电感电流纹波可以减小50%以上,有利于减小电感体积和重量。
参考文献
[1] 王剑, 张芮, 刘洋, 等. 一种QZS-CHI的多调制波移相正弦脉宽调制方法及其输出电压分析[J]. 电工技术学报, 2020, 35(16): 3470-3477.
Wang Jian, Zhang Rui, Liu Yang, et al. A multi-modulation waveform phase-shift sinusoidal pulse width modulation method of QZS-CHI and its output voltage analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3470-3477.
[2] 程启明, 江畅, 沈磊, 等. 准Z源三电平并网逆变器的无源控制策略[J]. 电工技术学报, 2020, 35(20): 4361-4372.
Cheng Qiming, Jiang Chang, Shen Lei, et al. Passivity-based control strategy of quasi Z-source three-level grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4361-4372.
[3] 吴昊坤, 黄科元, 吕维, 等. 用于高速永磁电机的Z源逆变器直流链电压控制策略[J]. 电工技术学报, 2020, 35(16): 3489-3497.
Wu Haokun, Huang Keyuan, Lü Wei, et al. Z-source inverter DC-link voltage control strategy for high speed permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3489-3497.
[4] Fang Xupeng, Tian Yingying, Ding Xiaokang, et al. Series-type switched-inductor Z-source inverter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 53-60.
[5] Noroozi N, Yaghoubi M, Zolghadri M R. A short-circuit fault diagnosis method for three-phase quasi-Z-source inverters[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 672-682.
[6] Meraj M, Rahman S, Iqbal A, et al. Novel level-shifted PWM technique for equal power sharing among quasi-Z-source modules in cascaded multilevel inverter[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4766-4777.
[7] 彭方成, 范学鑫, 王瑞田, 等. 大容量DC-DC变流器输出阻抗特性分析及应用[J]. 电工技术学报, 2021, 36(16): 3422-3432.
Peng Fangcheng, Fan Xuexin, Wang Ruitian, et al. Analysis and application of output impedance characteristics of high-capacity DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3422-3432.
[8] 乔扬, 张笑天, 杨旭. 具有短路限流能力的大变比DC/DC变换器[J]. 电力系统自动化, 2020, 44(5): 47-52.
Qiao Yang, Zhang Xiaotian, Yang Xu. Large-step-ratio DC/DC converter with capability of short-circuit current limiting[J]. Automation of Electric Power Systems, 2020, 44(5): 47-52.
[9] 倪梦涵, 杨晓峰, 王淼, 等. 多电平均压型直流变换器输入电流纹波抑制策略[J]. 电工技术学报, 2021, 36(16): 3354-3364.
Ni Menghan, Yang Xiaofeng, Wang Miao, et al. Input Current ripple suppression strategy of multilevel voltage-balancing DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3354-3364.
[10] Peng Fang zheng. Z-source inverter[J]. IEEE Transactions on Industry Applications, 2003, 39(2): 504-510.
[11] 屈艾文, 陈道炼, 苏倩. 三相准Z源并网逆变器的简单升压改进空间矢量调制策略[J]. 电工技术学报, 2018, 33(4): 826-836.
Qu Aiwen, Chen Daolian, Su Qian. Simple boost modified space vector modulation strategy for three-phase quasi-Z-source grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 826-836.
[12] 王灿, 杜船, 徐杰雄. 中高压直流断路器拓扑综述[J]. 电力系统自动化, 2020, 44(9): 187-199.
Wang Can, Du Chuan, Xu Jiexiong. Review of topologies for medium- and high-voltage DC circuit breaker[J]. Automation of Electric Power Systems, 2020, 44(9): 187-199.
[13] 程启明, 李涛, 程尹曼, 等. 基于受控耗散Hamiltonian系统模型的光伏准Z源T型三电平并网逆变器控制策略[J]. 电工技术学报, 2019, 34(8): 1718-1727.
Cheng Qiming, Li Tao, Cheng Yinman, et al. Control strategy of PV quasi-Z-source T-type three-level inverter based on port controlled Hamiltonian with dissipation model[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1718-1727.
[14] Ho A V, Chun T W, Kim H G. Extended boost active-switched-capacitor/switched-inductor quasi-Z-source inverters[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5681-5690.
[15] Chauhan A K, Raghuram M, Singh S K. Nonzero discontinuous inductor current mode in certain Z-source converters[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 2809-2814.
[16] Dong Shuai, Zhang Qianfan. CCM and DCM analysis of ASC-qZSIs[J]. IET Power Electronics, 2019, 12(8): 2049-2057.
[17] Nguyen M K, Choi Y O. PWM control scheme for quasi-switched-Boost inverter to improve modulation index[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4037-4044.
[18] Nguyen M K, Tran T T, Lim Y C. A family of PWM control strategies for single-phase quasi-switched-Boost inverter[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1458-1469.
[19] Tran T T, Choi J H, Nguyen M K, et al. A novel space vector modulation strategy for three-phase quasi switched Boost inverter[C]//2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), Busan, Korea (South), 2019: 1084-1089.
[20] Liu Yushan, Ge Baoming, Abu-Rub H, et al. Overview of space vector modulations for three-phase Z-source/quasi-Z-source inverters[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 2098-2108.
[21] Ali U S, Kamaraj V. A novel space vector PWM for Z-source inverter[C]//2011 1st International Conference on Electrical Energy Systems, Chennai, India, 2011: 82-85.
[22] Dong Shuai, Zhang Qianfan, Cheng Shukang. Inductor Current ripple comparison between ZSVM4 and ZSVM2 for Z-source inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7592-7597.
A Novel Space Vector Modulation Method for Three-Phase Quasi-Switched-Boost Inverter to Minimize Inductor Current Ripple
Abstract The high frequency current ripple affects the volume and weight of the converter inductor. For the quasi-switched-Boost inverter, the traditional shoot-through modulation algorithm cannot minimize the inductor current ripple. A space vector modulation method with the minimum inductor current ripple was proposed to redistribute the turn-on and turn-off sequences of the switches. On this basis, the mathematical relationship between the shoot-through ratio and the conduction duty ratio was derived. Finally, the performance of the proposed modulation algorithm and the traditional algorithm in suppressing the inductor current ripple was compared by simulations and experiments. The results can agree with the theoretical analysis.
keywords:Quasi-switched-Boost inverter, current ripple, shoot through, space vector modulation
DOI:10.19595/j.cnki.1000-6753.tces.211070
中图分类号:TM464
国家自然科学基金资助项目(51807032)。
收稿日期 2021-07-15
改稿日期 2021-10-13
董 帅 男,1987年生,副教授,博士生导师,研究方向为无线电能传输。E-mail:dongshuai@hit.edu.cn (通信作者)
林 晨 男,1999年生,硕士,研究方向为无线电能传输。E-mail:321158570@qq.com
(编辑 郭丽军)