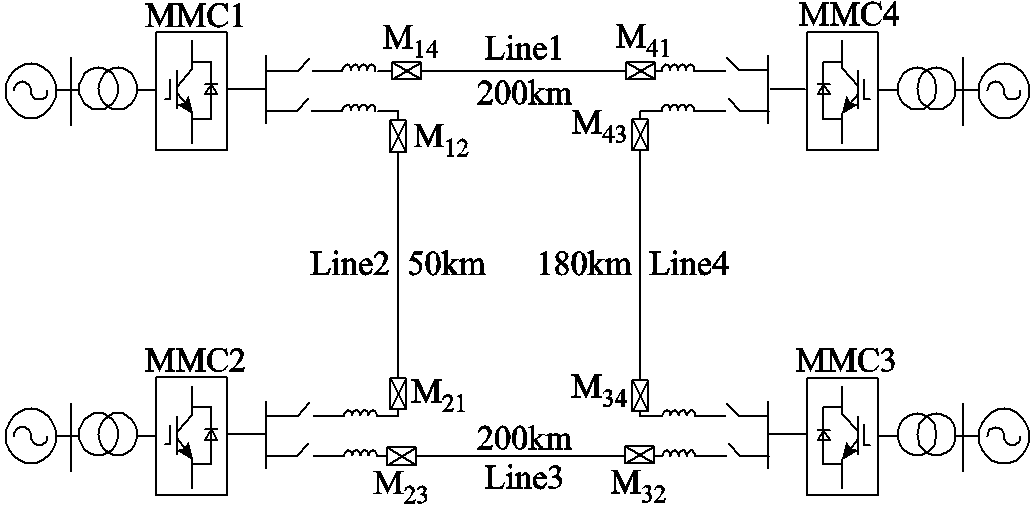
图1 柔性直流电网单线图
Fig.1 Flexible DC grid single line diagram
摘要 柔性直流电网线路发生故障时，线路保护装置需要快速可靠地切除故障线路以保证非故障线路能正常运行，进而提高输电系统的安全性和可靠性。为此提出柔性直流电网快速纵联保护的线性回归方法。首先分析模块化多电平换流器（MMC）等效阻抗和平波电抗器形成的物理边界对高频分量的衰减作用，其次分析输电线路单极故障和双极故障时的电流回路以及非故障线路的电流流通情况，然后根据输电线路的电压突变的能量作为保护的启动判据，利用短时窗电流的回归系数来进行区内外故障识别和故障选极；最后，在PSCAD上搭建柔性直流电网仿真模型对保护方案进行验证，仿真结果表明，该保护方法能准确可靠地甄别故障，速动性好，具有较好的耐过渡电阻能力和适用性。
关键词：柔性直流电网 模块化多电平换流器物理边界 线性回归 故障检测 线路保护
近年来我国中西部地区的新能源发展迅速，高比例的可再生能源决定了在新型电力系统中需要更加灵活的并网技术，因此区域电网互联成为时代背景下的大趋势[1-4]。为给弱交流或无源交流系统提供电源支撑并提高输电系统的稳定性，将多端直流输电系统应用于区域电网互联场景中。然而传统的高压直流输电系统由于直流电网的电压极性恒定不变，电流只能单向流通，潮流难以反转，难以实现电网互联，而柔性直流输电系统中电流可以双向流通[5]，直流电网的潮流方向可以改变，适合构成多端直流系统，例如已投入运行的张北示范工程在直流侧将输电线路互相连接起来，当某一条线路故障时，可将该线路的潮流转移到非故障线路，从而提高输电系统的可靠性[6-8]。因此，从输电系统的运行灵活性和供电可靠性角度出发，多电源供电和多落点受电的柔性直流电网成为新型电力系统的发展趋势之一。
随着柔性直流输电的不断发展，远距离、大容量的架空线路输电成为一个趋势，相比于电缆线路，架空线路更容易发生故障，当直流输电线路发生故障时，换流站中子模块电容放电，在数毫秒内故障电流达到较大的过电流水平[9]，若不能快速将故障线路切除，将导致换流器闭锁，可能发生停电事故。为保证直流故障下换流器不闭锁，保证非故障线路能正常运行，提高输电系统的可靠性，必须快速准确地清除故障。
针对柔性直流电网线路保护问题，国内外学者已经展开了广泛研究[10-14]。文献[15]针对纵联电流差动保护通过较长延时来防止线路分布电容等引起的误动，从而无法满足保护对速动性要求的问题，提出了一种采用电流突变量夹角余弦值的纵联保护方法，该方法有较强的耐过渡电阻能力，但该方法利用的是全电流量，在线路重载情况下发生高阻故障时，故障线路两端的全电流的极性可能相反，此时该保护方法不能可靠识别区内故障。文献[16]针对传统柔性直流输电线路保护动作时间过长，无法满足速动性要求的问题，提出了采用行波保护、电压突变量保护与电流突变量保护相结合的方式实现直流短路故障的快速检测和定位，但其行波保护、电压突变量保护以及电流突变量保护的整定值不易确定，且文中未考虑过渡电阻及线路分布电容的影响。文献[17]分析了直流线路的故障行波特征，提出了基于单端量初始行波的保护方案和雷击干扰的快速识别方法，该保护方法在保证速动性的同时提升
了保护的可靠性。文献[18]提出一种基于线路边界元件的新型快速方向纵联故障识别方法，该方法具有较强的抗噪声能力、较好的速动性和较强的耐过渡电阻能力，但该保护方案是基于以电抗器为边界而提出的，不适用于无线路边界的输电系统。文献[19]为了提高柔性直流线路保护的可靠性和灵敏度，确保能准确识别故障区域，提出基于主动探测式的直流电网纵联保护方法，但该方法需要8ms时窗长的数据进行计算，时窗较长。在张北柔直电网中，线路上配置有断路器，保护系统需要在6ms内实现故障的隔离和清除，其中短路的动作时间为3ms，则要求保护装置在3ms内正确动作，因此考虑到保护的速动性，文献[20]提出了柔性直流电网线路保护配置方案。
因此，本文针对柔性直流电网线路保护的问题，分析了输电线路的边界特性和线路故障的故障特性，并提出了基于线性回归的柔性直流电网纵联保护方法，该方法利用较短时窗内电流故障分量的线性回归系数进行区内外故障识别和故障选极，不依赖线路边界特性，不受线路分布电容的影响，耐过渡电阻能力强。最后在PSCAD/EMTDC中搭建仿真模型，大量仿真实验验证了该保护方法在不同工况下的有效性。
四端MMC-HVDC系统结构单线图如图1所示，MMC2和MMC3容量为3 000MW，MMC1和MMC4容量为1 500MW，电网采用对称双极接地方式， Mij（i, j=1, 2, 3, 4，i≠j）表示输电线路两端配置的保护安装点，输电线路两端均有平波电抗器，各输电线路长度已在图中标注。
图1 柔性直流电网单线图
Fig.1 Flexible DC grid single line diagram
MMC换流器拓扑结构如图2所示，图中uj和ij（j=a, b, c）分别为交流侧电压和电流；uSM为子模块的输出电压；UC为电容电压；Udc为直流电压；Rs、R0分别交流侧等效电阻和桥臂电阻，Ls、L0分别交流侧等效电感和桥臂电感，C0为子模块电容。
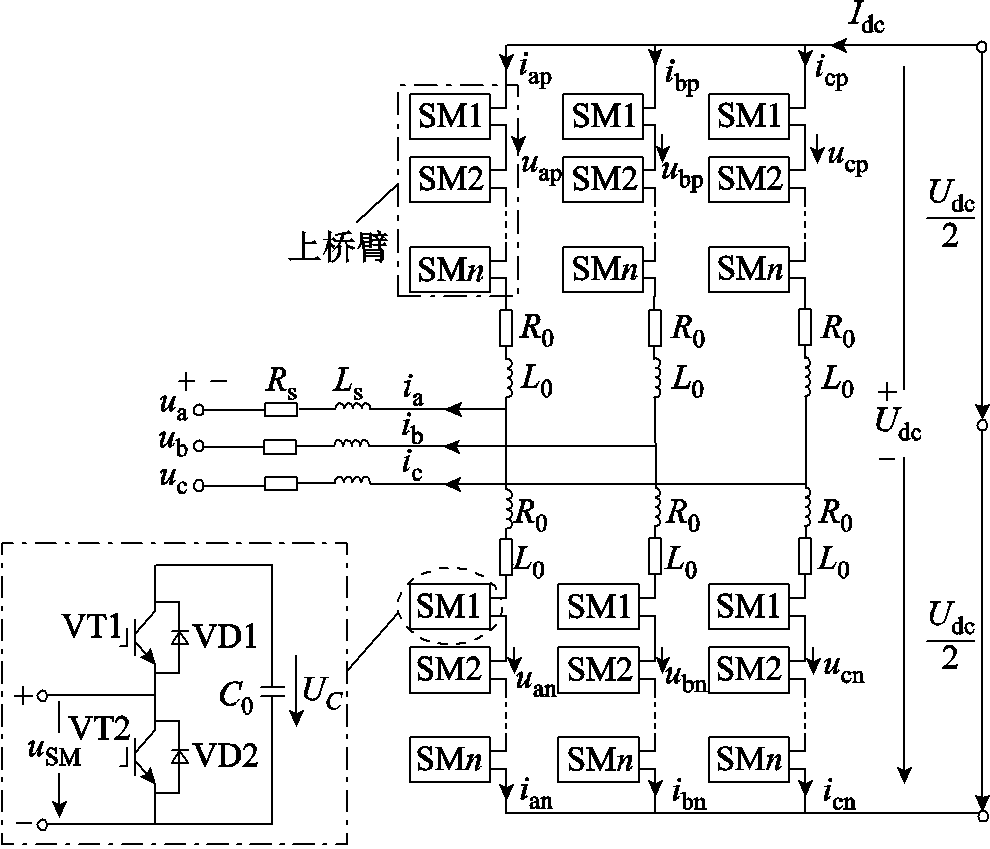
图2 MMC拓扑结构
Fig.2 Topology of MMC
对于a相，上、下桥臂分别满足KVL方程，即有
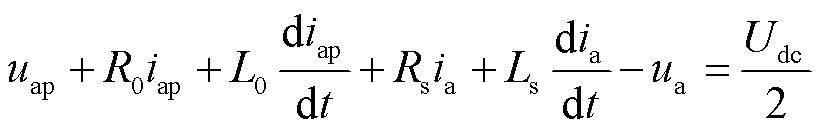（1）
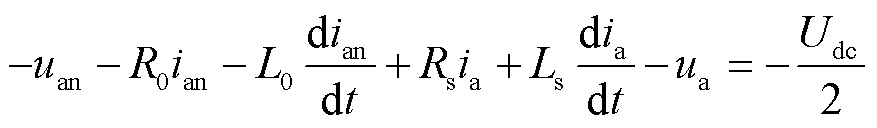（2）
将式（1）和式（2）相减后再对a、b和c三相进行叠加可得
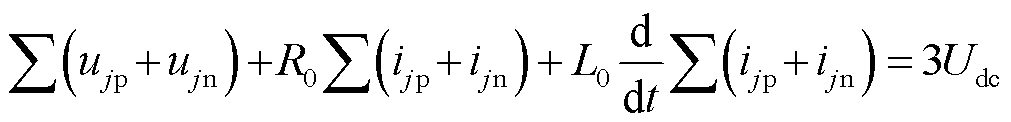（3）
在图1所示的拓扑结构中有
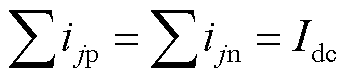（4）
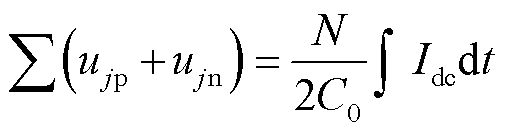（5）
式中，N为上、下桥臂投入的子模块数量。
因此式（3）可以简化为
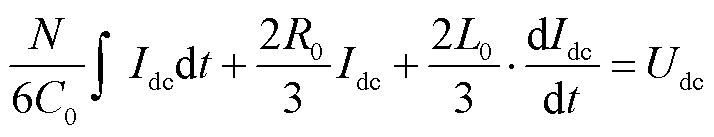（6）
对式（6）进行正弦稳态分析得
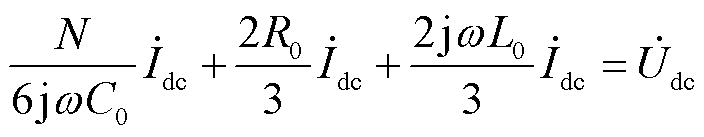（7）
由式（7）可知，MMC直流侧可由电阻、电容和电感元件串联进行等效，由于存在换流站和线路两端平波电抗器形成的边界，使得交流侧故障和输电线路故障时在线路保护测量点处呈现的特性不同，该物理边界的等效阻抗模型如图3所示，其中R0=0.005W，L0=30mH，C0=2 500mF，L1=150mH，N=200。
图3 等效阻抗模型
Fig.3 Equivalent impedance model
该边界等值阻抗为
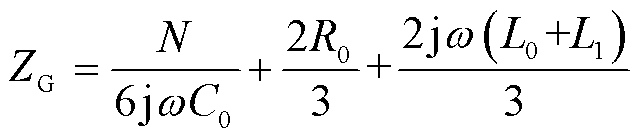（8）
根据系统的结构参数，得出等值阻抗的阻抗频率特性如图4所示，物理边界的谐振频率f0=54Hz，当频率大于1kHz时，随着频率的增加，边界阻抗值线性增加，呈现感抗特性，该阶段边界对高频信号有一定的衰减作用。
图4 MMC等效阻抗频率特性
Fig.4 Equivalent impedance frequency characteristic of the MMC
区外故障时故障分量传播到保护测量点处时都经过了该物理边界，因此保护测量点测出的故障分量的幅值和陡度都较小，区内故障时故障分量传播到保护测量点时未经过物理边界，因此保护测量点测出的故障分量的幅值和陡度都较大。
同理，在柔性直流电网中，当线路i故障时，线路j两端保护测得的电气量经过由平波电抗器形成的边界，电感在高频情况下呈现较大的阻抗特性，因此，故障量从故障线传到非故障线路时高频分量存在极大的衰减。
以线路1正极发生接地故障分析张北四端柔性直流电网的单极接地故障特性，当发生正极接地故障时，电流故障分量在经过保护安装处之后有两条流通路径，其中，一条流到换流站，另一条流到线路，由于换流站采用真双极接线方式，四端换流站均可以通过对应的中性接地点与故障点形成故障回路。以换流站1为例，换流站闭锁前故障电流的流通回路如图5虚线所示，故障电流从故障点流向接地点，电流故障分量经保护安装处M之后，一部分流往换流站1，另一部分流往线路2的正极。
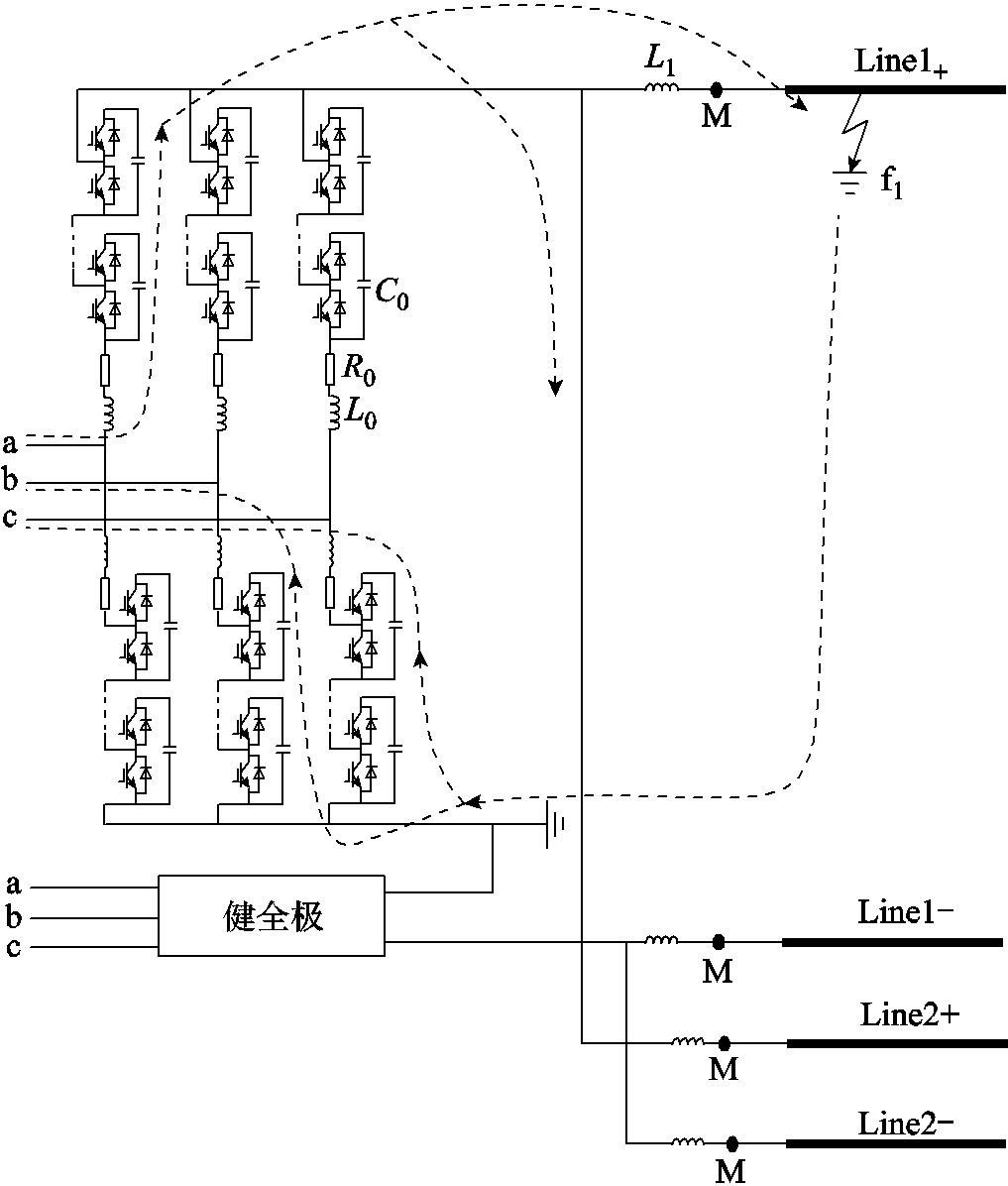
图5 单极接地故障电流流通回路
Fig.5 Single pole line-to-ground fault current flow loop
当线路发生单极接地故障时，换流站所在支路由切除的子模块的反并联二极管、投入运行的子模块的绝缘栅双极晶体管IGBT和并联电容C0构成，同时交流侧系统会通过子模块中的反并联二极管向短路点注入短路电流，因此闭锁前各桥臂中的电流是子模块并联电容放电电流和交流侧电流的叠加，但故障回路中主要以子模块电容放电为主，交流侧几乎不参与放电过程，因此后续分析将忽略交流侧馈入电流的影响。
正极接地故障时，四端柔直电网的等效电路如图6所示，根据1.1节的分析，将各换流站等效为电阻、电感和电容元件的串联。
图6 单极接地故障等效电路
Fig.6 Single pole line-to-ground fault equivalent circuit
将各个换流站的电阻、电感和电容的串联组合分别作为一条支路；将每条健全线路分别作为一条支路；将故障线从故障点分为两条支路，则图5的等效电路如图6所示，节点数为4，支路数为9，其中支路1～支路4为各换流站等效支路，支路5和支路6为故障线路等效支路，支路7～支路9为各健全线路等效支路。以节点为参考，并规定节点①、②、③、④的节点电压分别用un1、un2、un3、un4来表示。支路电压分别用u1、u2、u3、u4、u5、u6、u7、u8、u9来表示。
根据基尔霍夫电压定律可得，u1=u5=un1，u2=u6= un2，u3=un3，u4=un4，u7=un3-un2，u8=un4-un3，u9= un1-un4。
现计算各节点电压，节点①～节点④的电压即为换流站1～换流站4出口处的电压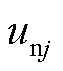
（j=1, 2, 3, 4）为
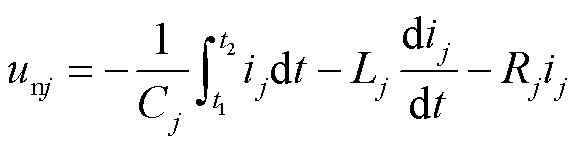（9）
式中，Cj、Lj和Rj分别为4个换流站的等效电容、等效电感和等效电阻。
另外，节点①处和节点②处的电压还可分别表示为
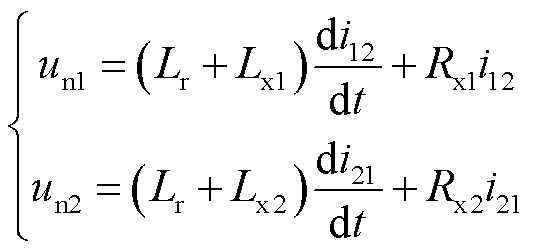（10）
式中，Lr为平波电抗器的大小；Lx1和Lx2、Rx1和Rx2分别为故障点到故障点所在线路两端的线路等值电抗、线路等值电阻。
现计算各支路电压，由图7可知，支路1～支路6的支路电压即为各自的节点电压，支路7～支路9的支路电压分别为
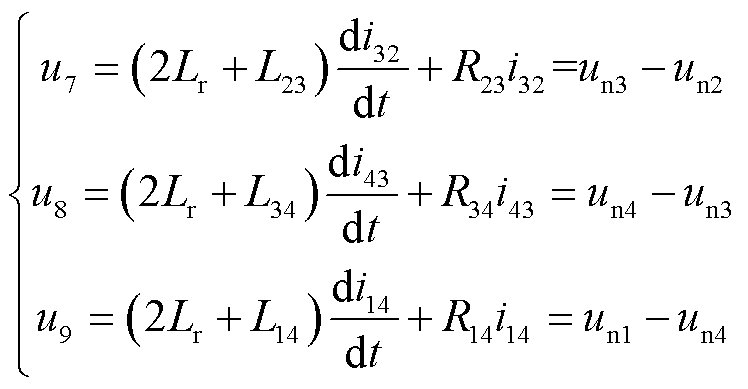（11）
如图6所示，若不考虑架空线路分布电容电流的影响，则健全线路两侧电流幅值相等，则有
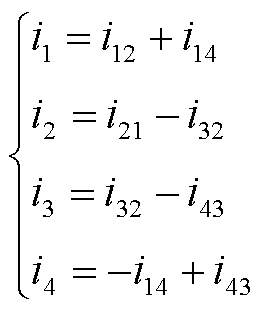（12）
结合方程式（9）～式（11）并求导，再结合式（12）可得
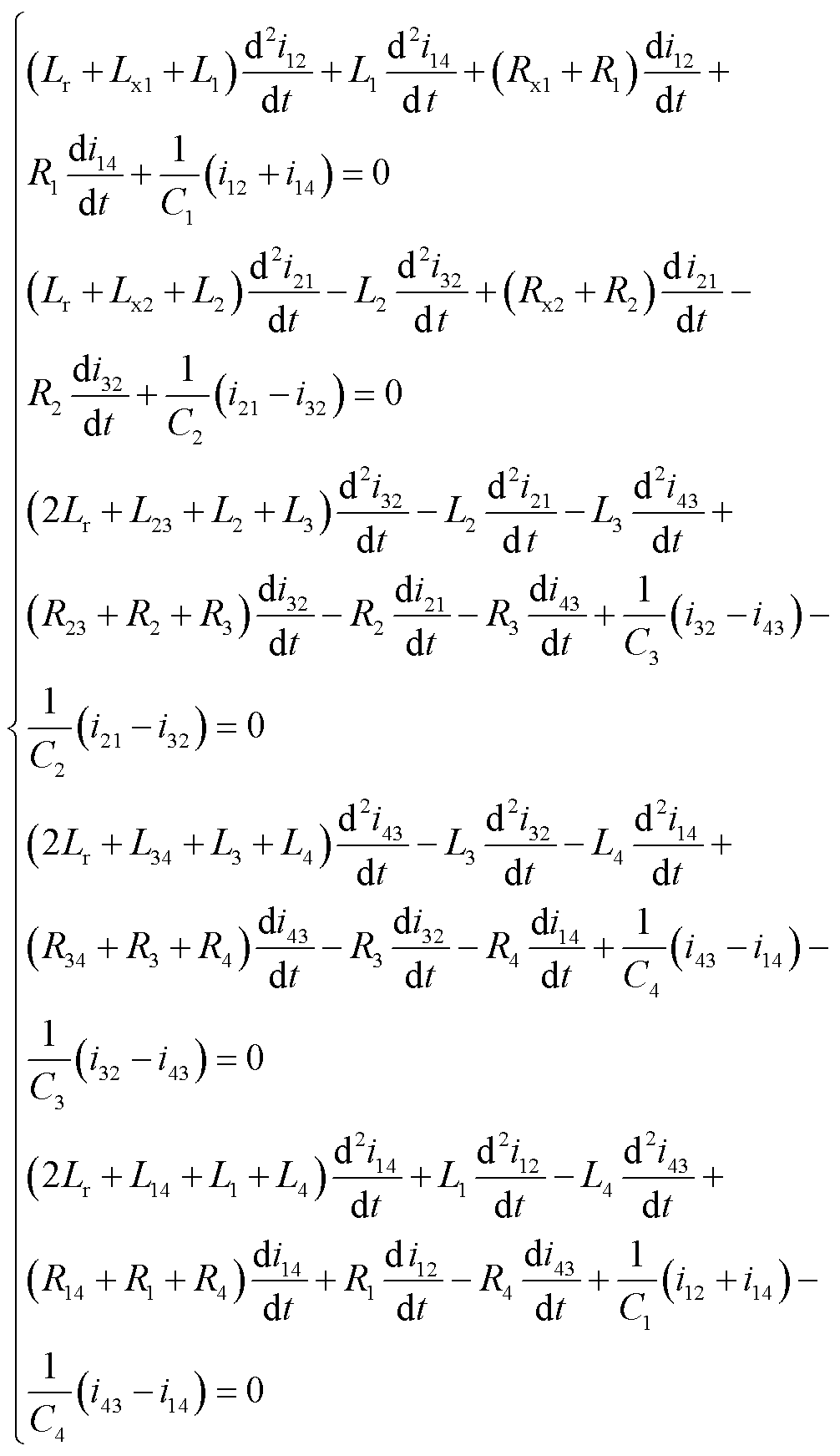（13）
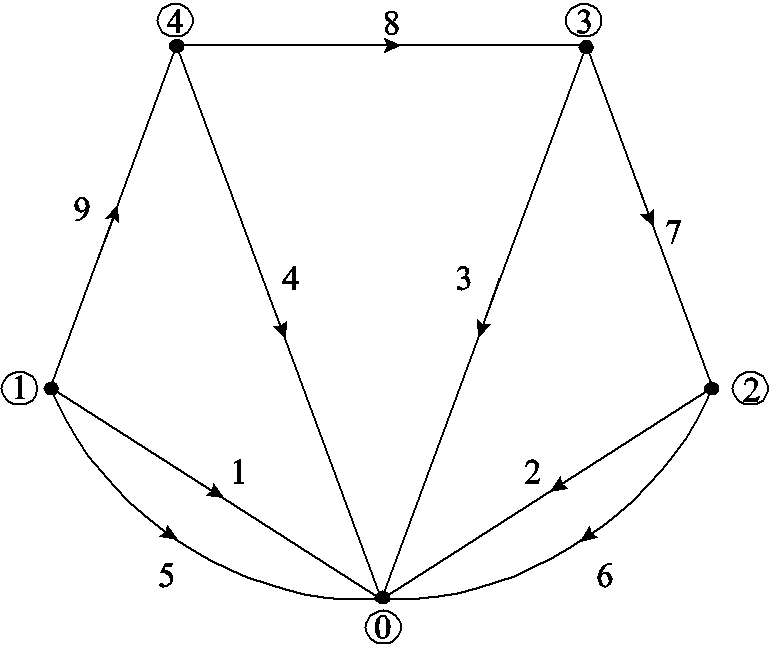
图7 等效电路的有向图
Fig.7 Graph of equivalent circuit
根据各线路的电流初始值及式（13）即可求出各线路的故障电流。如图8所示，理论值和仿真值吻合度较高，由理论值和仿真值可知，故障线路两端的电流变化趋势相同且上升较快，而非故障线路电流上升缓慢。
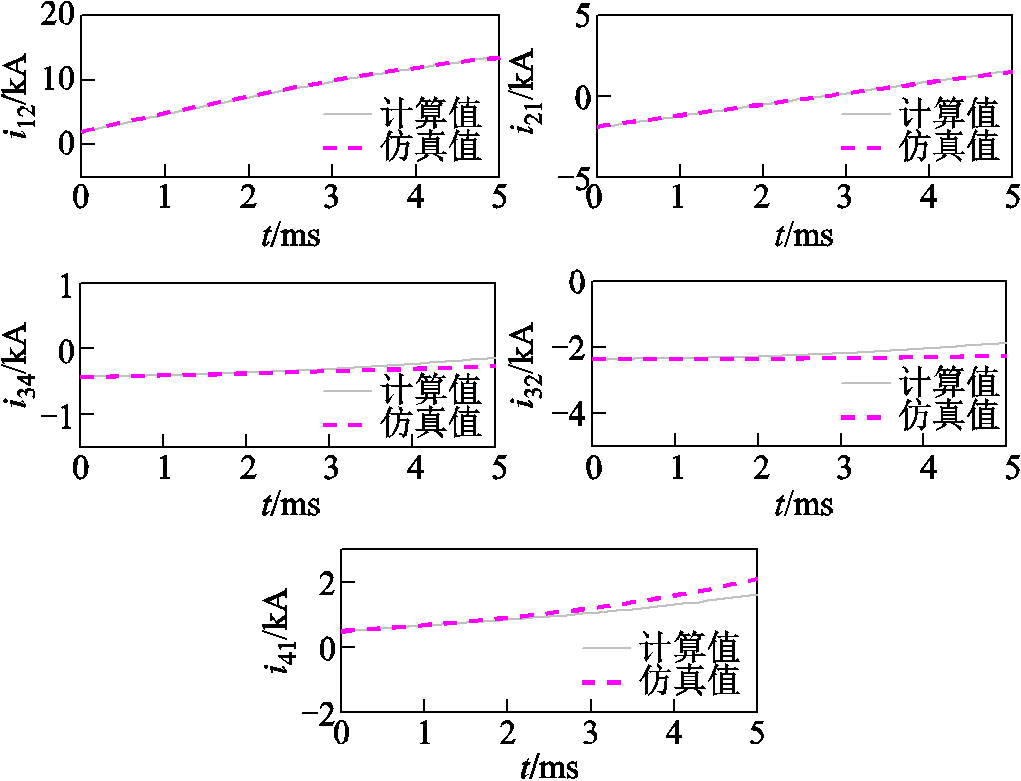
图8 仿真值与计算值比较
Fig.8 Comparison of calculated value and simulated value
当线路1发生双极短路故障时，故障电流流通回路主要是两个部分的叠加，即故障点处的正极接地故障和负极接地故障的叠加，因此，发生双极短路故障后，电流故障分量在经过正极和负极保护安装处之后各有两条流通路径，流通路径类似正极接地故障，此处不再赘述。
以线路1发生正极接地故障为例，根据1.2节对单极接地故障的特性分析，可等效得到图9所示的故障分量网络，图9中，对于保护M14和M41来说，故障f1为区内故障，对于保护M12、M21、M23、M32、M34和M43来说，故障f1为区外故障，Di14、Di41、Di12、Di21、Di23、Di32、Di34和Di43分别为线路1～4两端保护装置测量的电流故障分量，规定电流由母线流向线路方向为正。
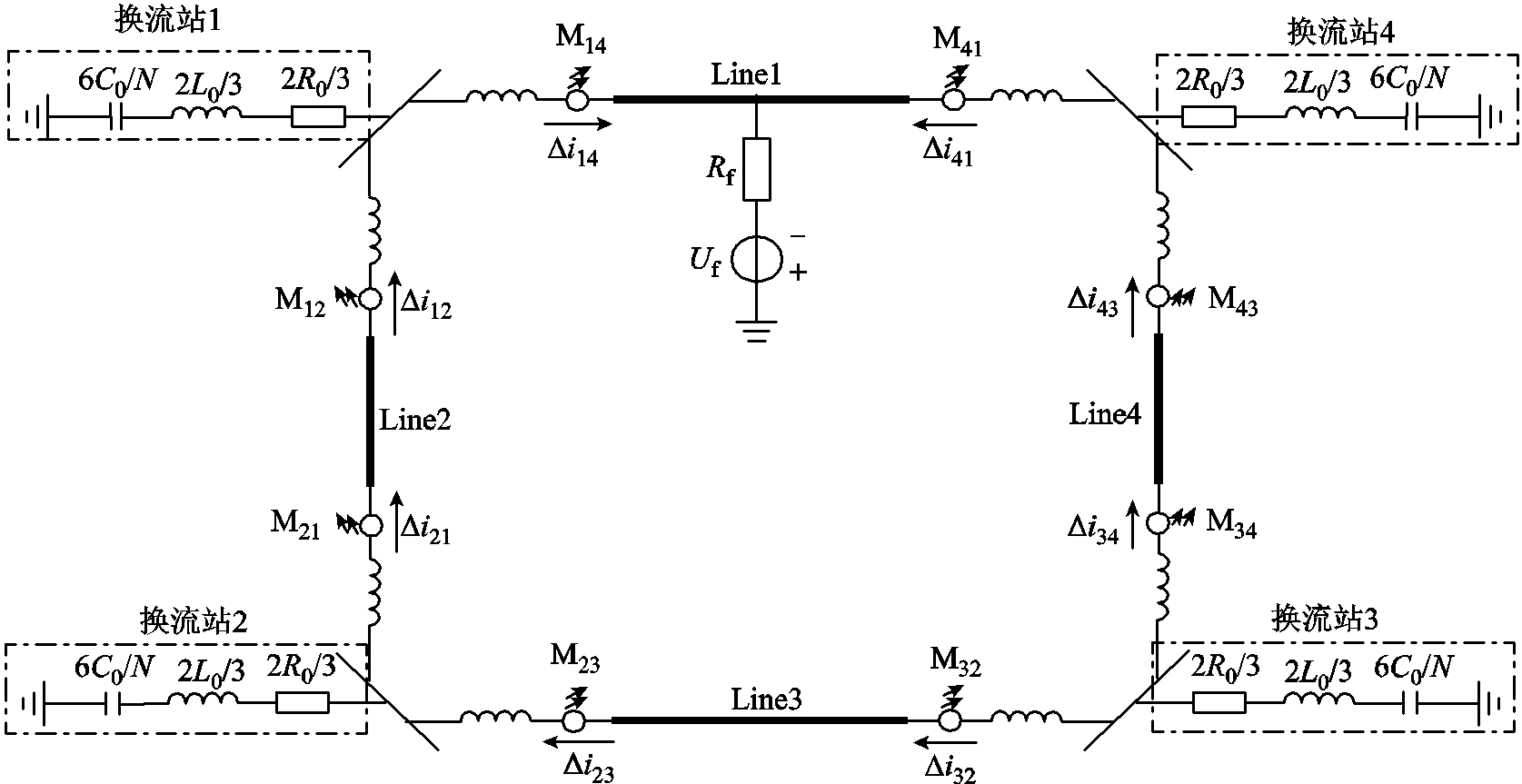
图9 线路1正极接地故障分量网络
Fig.9 Line1 positive pole ground fault component network diagram
当线路1发生故障时，其两端的电流故障分量的变化方向相反，非故障线路两端的电流故障分量变化方向相同，由于线路两端的平波电抗器对高频分量的阻抗很大，频率越高，阻抗越大，故障线路两端测量点测出的电流故障分量未经过平波电抗器，其幅值和陡度都较大，而电流故障分量传播到非故障线路时都经过平波电抗器，因此进入非故障线路的电流故障分量的幅值和陡度都较小。
在双极输电系统中正负极输电线路间存在电磁耦合作用，采用Clarke相模变换将正负极电压Up、Un和正负极电流Ip、In解耦为独立的线模分量和零模分量，即对直流线路的电压和电流分别进行相模变换得到对应的线模U1、I1和零模U0、I0为
（14）
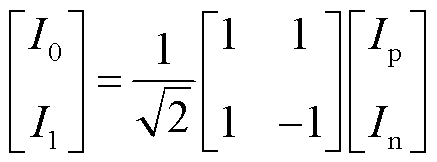（15）
由于零模电气量在传播过程中衰减严重，且零模电气量只存在于接地故障情况下，而线模电气量不仅存在于接地故障还存在于极间故障，因此利用线模量更能适用于不同故障类型的分析。
利用线模电压计算电压突变量为
（16）
式中，j为当前采样点。
用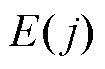
表示电压突变的能量，即
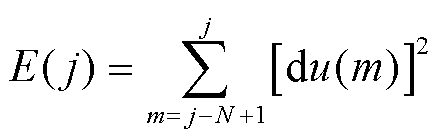（17）
式中，N为一定时窗内的采样点数，在文中N取5。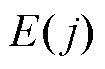的运算是对线模电压先进行微分后进行积分的运算，具有突出信号的变化量和平抑高斯噪声的作用。
当系统正常运行时，电压突变量
和能量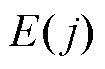的理论值为零；当线路发生故障时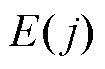，突变明显，因此利用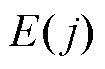构造启动判别式为
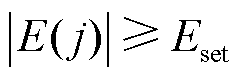（18）
若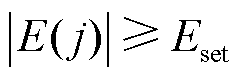，则线路故障保护元件启动，反之，则不启动。
考虑系统正常运行时，由于噪声干扰等因素使得电压幅值在额定值附近有一定的波动，则E(j)的值一般不为零，因此Eset的选择要大于正常运行时的电压突变能量最大值。在高压直流输电系统中，允许电压波动范围为2%，考虑最严重波动情况，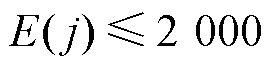
，考虑一定的裕度，本文将整定值Eset设置为2 400。
当输电线路发生故障时，故障线路两端的电流故障分量的变化方向相同，非故障线路两端的电流故障分量变化方向相反，由于线路两端的平波电抗器对高频分量的阻抗很大，故障线路两端测量点测出的电流故障分量还未经过平波电抗器，其幅值和陡度都较大，而电流故障分量传播到非故障线路时都经过平波电抗器，因此进入非故障线路的电流故障分量的幅值和陡度都较小。由理论值和仿真值可知，故障线路两端的电流变化趋势相同且上升得较快，而非故障线路电流上升缓慢。据此，可将短时窗内的电流进行线性回归处理，构造直线方程y=kx+b，利用回归系数k的正负来表征故障电流的突变方向，利用k绝对值的大小来表征故障电流的突变强度。
2.2.1 线性回归方法理论
回归分析是一种预测性的建模技术，它研究的是因变量和自变量之间的关系，这种技术通常用于预测分析时间序列模型以及发现变量之间的因果关系，常使用曲线来拟合数据点，目标是使曲线到数据点的距离差异最小[21]，为此，构建一次函数方程为
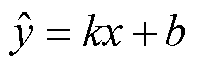（19）
式中，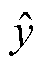
为预测值；x为自变量；y为因变量，为求解最佳参数k和b，需要一个标准来对结果进行衡量。针对任何模型求解问题，最终都是可以得到一组预测值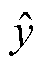，对比已有的真实值y，数据行数为n，可以将损失函数定义为
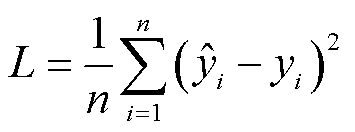（20）
将式（19）代入式（20）得
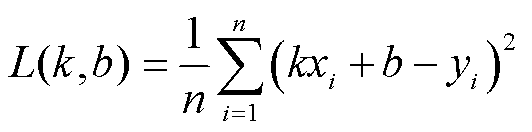（21）
为求解损失函数L最小化时对应的k和b的值，即核心目标优化式为
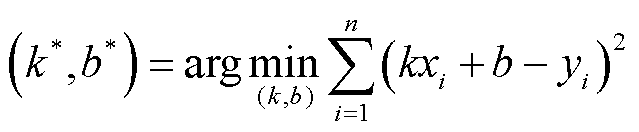（22）
求解k和b是使损失函数最小化的过程，在统计中，称为线性回归模型的最小二乘“参数估计”，现将L(k, b)分别对k和b求导[22]，得到
（23）
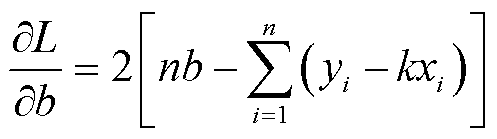（24）
令上述两式为0，可得到k和b最优解的闭式（closed-form）解为
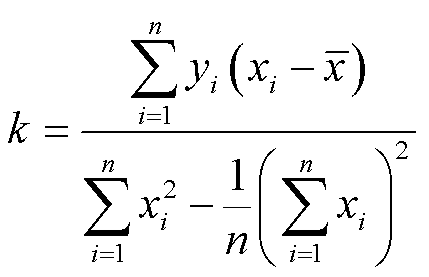（25）
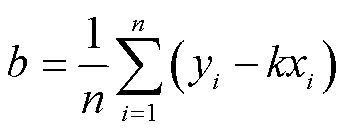（26）
为证明该线性回归方程的可靠性，可用显著性检验法和相关系数检验法进行检验，在本文中采用相关系数检验法。
回归平方和
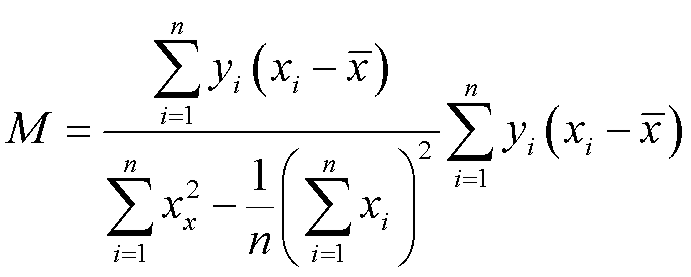（27）
剩余平方和
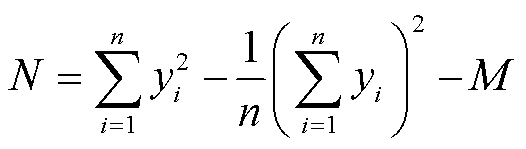（28）
相关指数
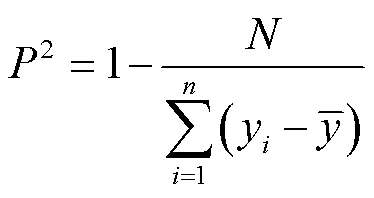（29）
则相关系数
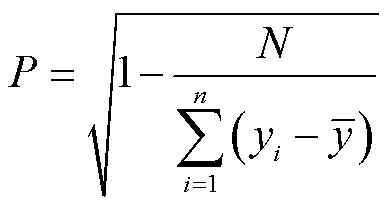（30）
相关系数P≤1，其值越接近1，说明回归直线的效果越好，可靠性也越大。
2.2.2 区内外故障识别判据
现以线路1发生单极接地故障为例，启动元件启动后，截取1ms时窗内的线模电流数据进行线性回归分析，并求出相关系数来检验回归方程的可靠性。根据式（19）、式（25）和式（26），可求得各线路线模电流的线性回归方程及其相关系数，求得线路1线模电流的线性回归方程为i1=1.358 4t+ 2.744 5，其线模电流曲线与线性回归曲线的相关系数为0.998 3；线路2线模电流的线性回归方程为i2=-0.188 7t-0.707 6，其线模电流曲线与线性回归
曲线的相关系数为0.929 4；线路3线模电流的线性回归方程为i3=-0.026 4t+3.474 6，其线模电流曲线与线性回归曲线的相关系数为0.992 8；线路4线模电流的线性回归方程为i4=0.156 9t-0.603 9，其线模电流曲线与线性回归曲线的相关系数为0.992 9，各线路线模电流及其线性回归曲线如图10所示。
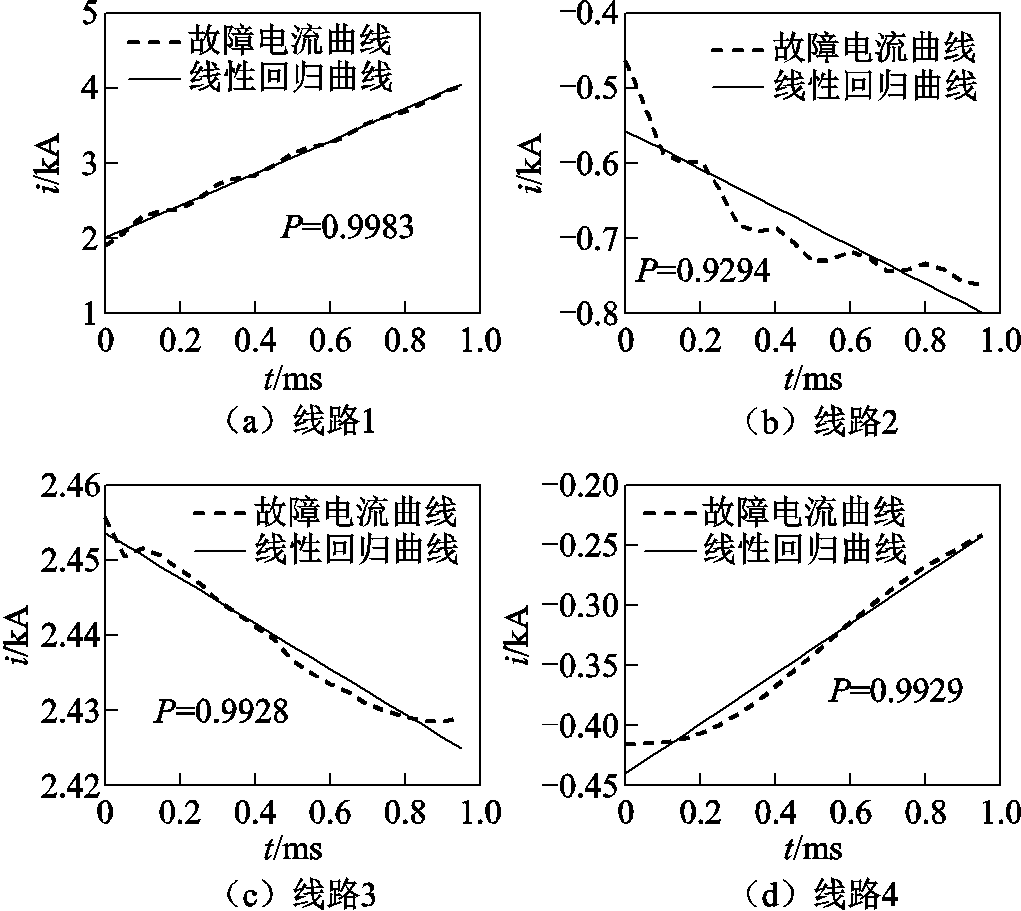
图10 各线路线模电流及其线性回归曲线
Fig.10 Line mode currents of each line and its linear regression curves
各条线路的线模电流曲线及其线性回归曲线的相关系数均接近于1，说明回归直线效果较好，线性回归方程有较高的可靠性，因此后续分析中用线性回归方程中的回归系数k的正负来表征故障电流的突变方向，利用k绝对值的大小来表征故障电流的突变强度。
当输电线路发生故障时，故障线路两端的电流故障分量的变化方向相同，则线路两端线模电流线性回归方程的回归系数同号；非故障线路两端的电流故障分量变化方向相反，线路两端线模电流线性回归方程的回归系数异号。其故障识别的计算式为
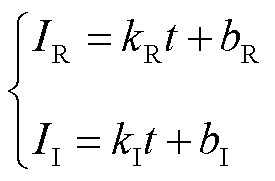（31）
式中，IR、II分别为线路两端线模电流线性回归后的预测值；kR、kI分别为线路两端线模电流线性回归方程的回归系数。
据此可形成线路故障识别判据为
（32）
当线路发生故障时，为使非故障线路能正常输送功率，要求故障线路的保护能可靠动作，因此快速准确选择出故障极对于输电系统的稳定运行起着至关重要的作用。
当发生单极接地故障时，故障点与系统中性接地点等电位，此时故障回路中的阻抗值远小于正常运行时的负荷阻抗值，电流快速增大，原则上非故障极电流不变，但由于正负极线路之间存在电磁耦合作用，因此非故障极电流也会增加，但远小于故障极；当发生双极短路故障时，正负极电流变化几乎相同。因此利用正负极电流分别进行线性回归后回归系数k绝对值的大小来表征故障电流的突变强度，故障极的k值远大于非故障极，故定义故障选极参数为
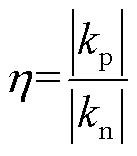（33）
式中，
为故障选极参数；kp、kn分别为正、负极电流进行线性回归后线性函数的回归系数。
当发生正极接地故障时，
1；当发生负极接地故障时，
1；当发生两极故障时，接近于1。为增大可靠性，引入可靠系数Krel=1.2，因此构造故障选极判据为
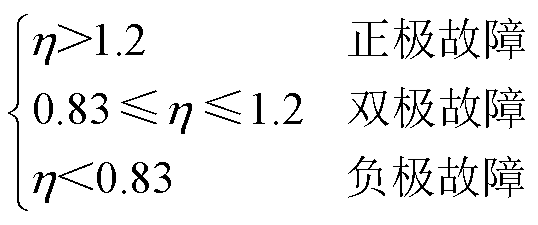（34）
本文的纵联保护方案主要包括保护启动、区内外故障识别和故障极判别。保护方案流程如图11所示。
具体可以分为以下几步：当线模电压突变的能量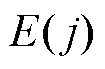
大于整定值时，保护启动；对启动后1ms时窗内的线模电流进行线性回归，计算回归后线性函数的k值；经过光纤通道，两端保护装置交换k值；根据两端k值的正负可以识别区内外故障，当kR、kI同号时，判定为区内故障，否则判断为区外故障；若判定为区内故障，则计算h，若h＞1.2，则判定发生正极故障，若0.83≤h≤1.2，则判定发生双极故障；若h＜0.83，则判定发生负极故障。
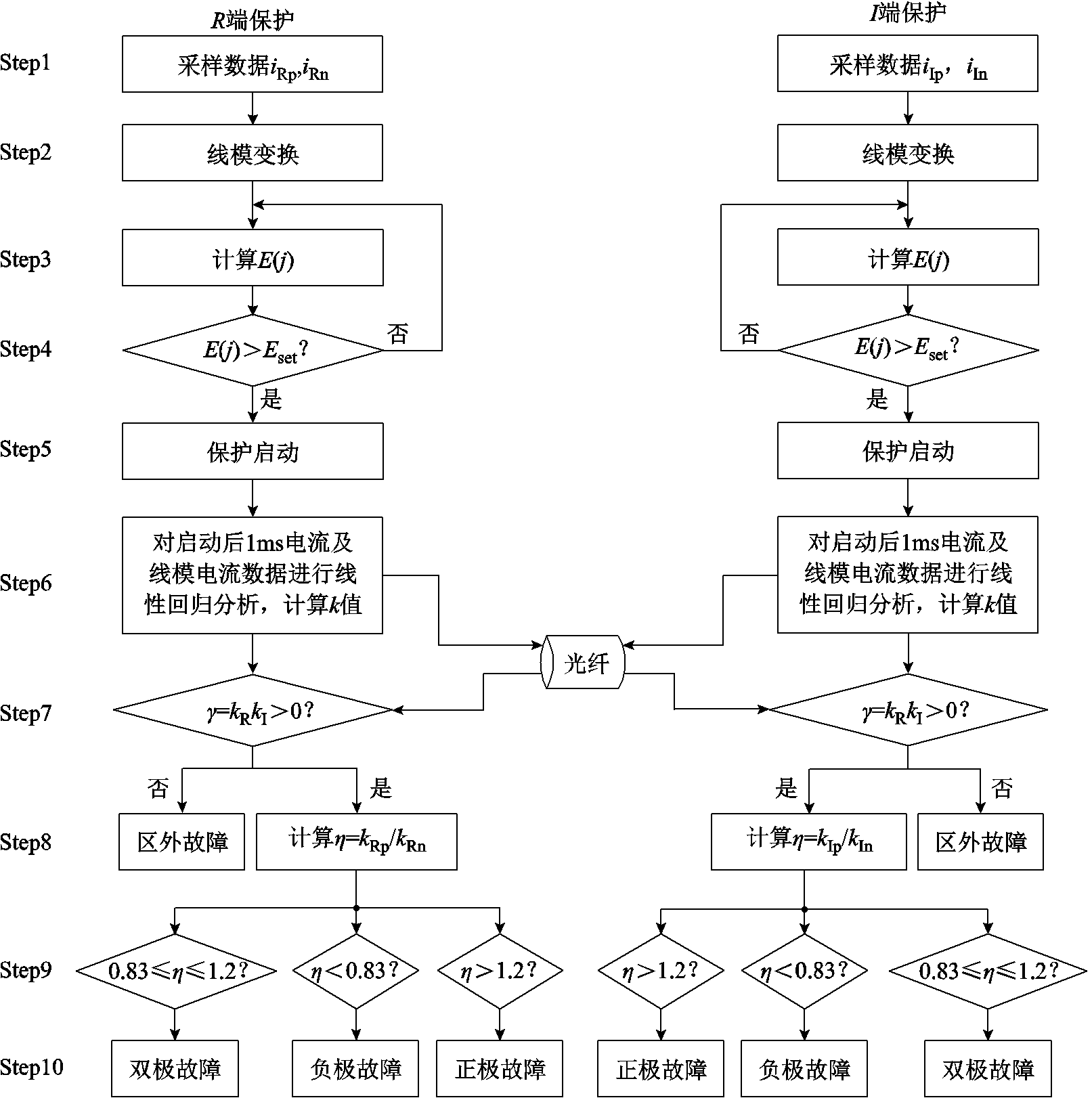
图11 保护方案流程
Fig.11 Flow chart of protection scheme
为验证本文保护方法的可靠性，在电磁暂态仿真软件PSCAD/EMTDC平台搭建四端柔性直流电网仿真模型，各参数参照张北柔性直流电网设置，见表1。
本文采样频率为20kHz，对线路i（i=1, 2, 3, 4）两端的保护来说，线路i发生的故障为区内故障，线路j（j≠i）（j=1, 2, 3, 4）的故障均为区外故障，在搭建的电网模型中设置不同工况下的直流线路故障，以验证所提保护方法的正确性及可行性。
表1 仿真系统的主要参数
Tab.1 Main parameters of simulation model
参数MMC1MMC2MMC3MMC4 换流站额定容量/(MV·A)1 5003 0003 0001 500 额定直流电压/kV500500500500 网侧额定电压/kV230230525525 阀侧额定定压/kV260260260260 桥臂子模块数N200200200200 子模块电容C0/mF2 5002 5002 5002 500 平波电抗器L/mH150150150150
若数据窗长越长，数据越多，则保护判断的准确性也越高，但是保护的速动性变差；由于采样数据中不可避免地存在噪声干扰，若数据窗越短，虽然提高了保护的速动性，但是降低了保护的可靠性，而可靠性是对继电保护性能的最根本要求，因此，应该选择合适的数据窗。
在2.2.1节中提到，利用相关系数检验法来验证线性回归方程与故障电流信号的相关性，即相关系数越高，线性回归方程与故障电流信号越契合，可靠性越高，则线性回归系数能更准确地反映故障电流的变化。现在故障电流信号中加入高斯噪声干扰，对不同时窗长的故障电流信号进行线性回归分析，并求出线性回归方程与故障电流信号的相关系数，见表2，数据窗长分别为0.4ms、0.6ms、0.8ms、1ms。
表2 不同数据窗的相关系数
Tab.2 Correlation coefficients of different lengths of data window
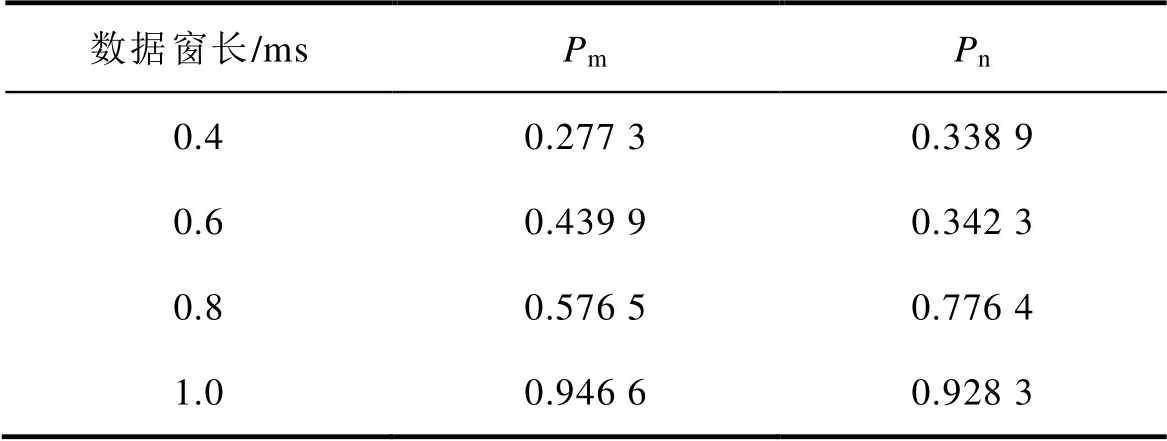
数据窗长/msPmPn 0.40.277 30.338 9 0.60.439 90.342 3 0.80.576 50.776 4 1.00.946 60.928 3
由表2可知，数据时窗越短，线性回归方程与故障电流信号的相关系数越小，即相关性越弱，则故障电流信号的线性回归效果不好，可靠性较低。当数据窗长为1ms时，线路两端的线性回归方程与故障电流信号的相关系数均接近1，线性回归效果较好，具有更高的可靠性。因此，选取分析时窗为1ms。
由于输电系统线路正负极是对称的，下文以正极线路发生故障来验证本文保护方法的正确性。线路1正极接地故障时，如图12所示，故障线路两端线模电流i14和i41的线性回归方程的回归系数k均为正，对于线路1两端的保护而言，该故障为区内故障；而非故障线路2、3和4两端线模电流的i12、i21、i23、i32、i34和i43的线性回归方程的回归系数k均为一正一负，对于线路2、3和4两端的保护而言，该故障为区外故障。
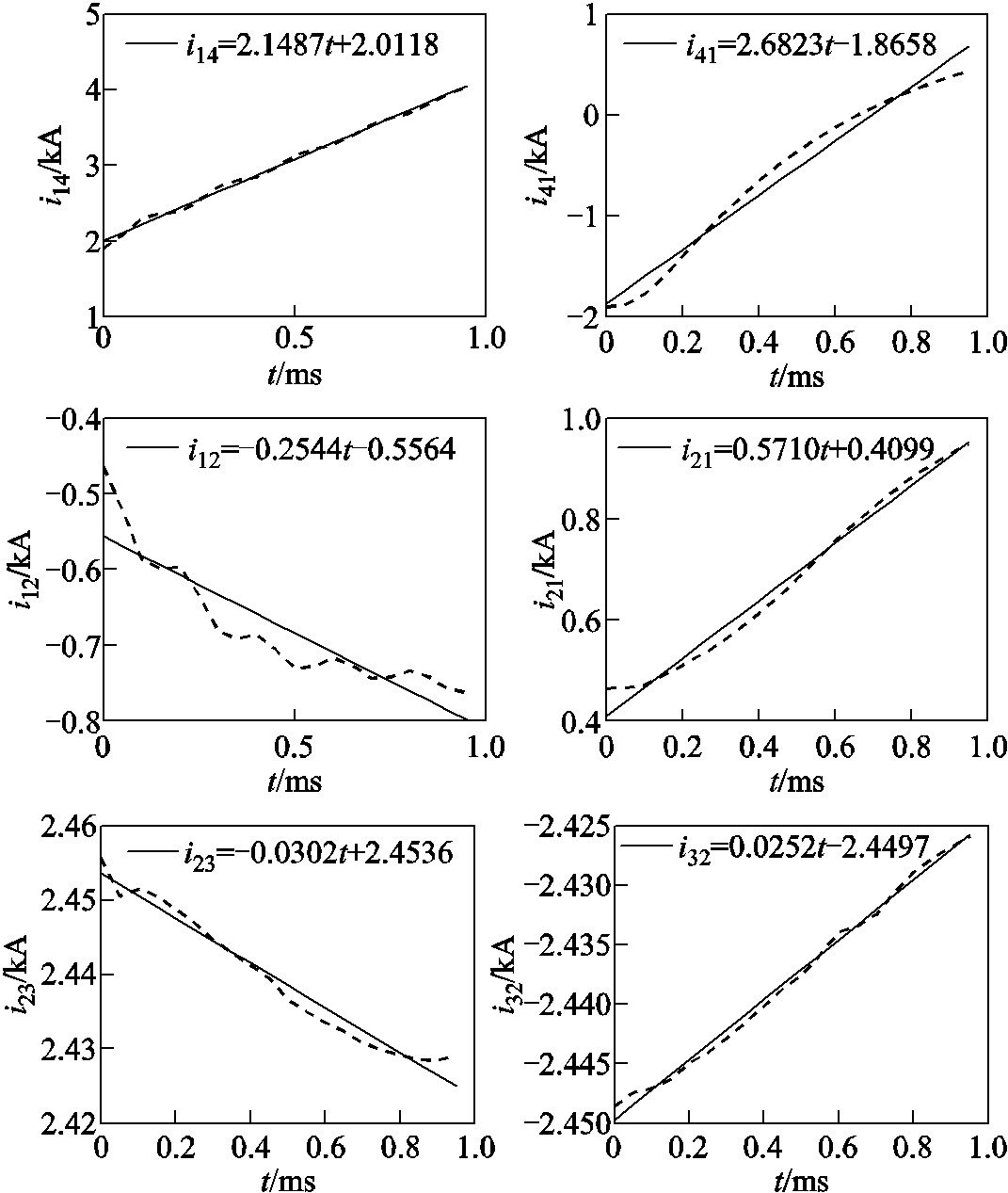
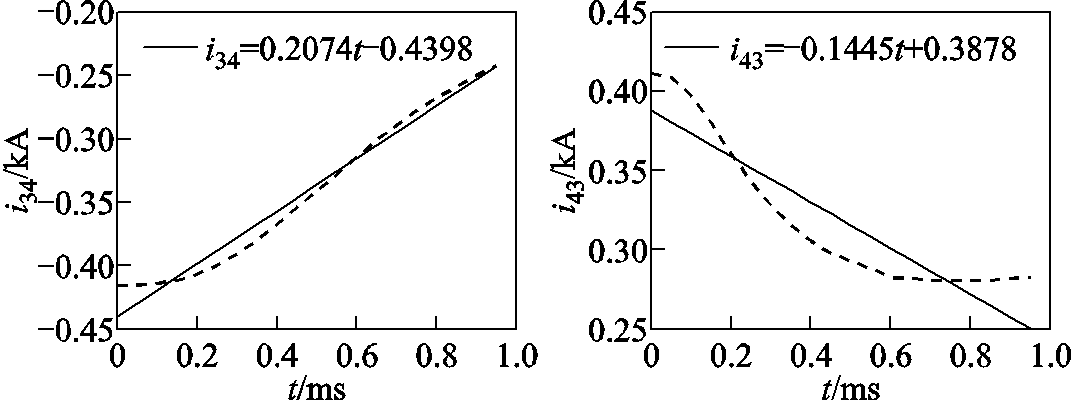
图12 线路1正极故障时各线路两端线模电流的线性回归方程及曲线
Fig.12 Linear regression equation and curves of line mode current at both ends of each line when the positive pole of Line1 failed
结合前文分析：当输电线路发生故障时，故障线路两端的电流故障分量的变化方向相同，非故障线路两端的电流故障分量变化方向相反，由于线路两端的平波电抗器对高频分量的阻抗很大，故障线路两端测量点测出的电流故障分量还未经过平波电抗器，其幅值和陡度都较大，而电流故障分量传播到非故障线路时都经过平波电抗器，因此进入非故障线路的电流故障分量的幅值和陡度都较小，说明仿真结果与理论分析一致。
直流输电系统正常运行时，电流的变化量接近于零，此时对电流线性回归得出的线性回归函数的回归系数为零，当单极接地故障时，故障极电流迅速增加，其线性回归函数的回归系数较大，由于两极间存在耦合作用，非故障极电流也会有变化，但变化很小，其线性回归函数的回归系数较小。如图13所示，正极和负极电流经线性回归后的线性函数回归系数分别为2.148 7和0.227 7，则故障选极参数h 为9.436 5，远大于整定值1.2，因此判定为正极故障。
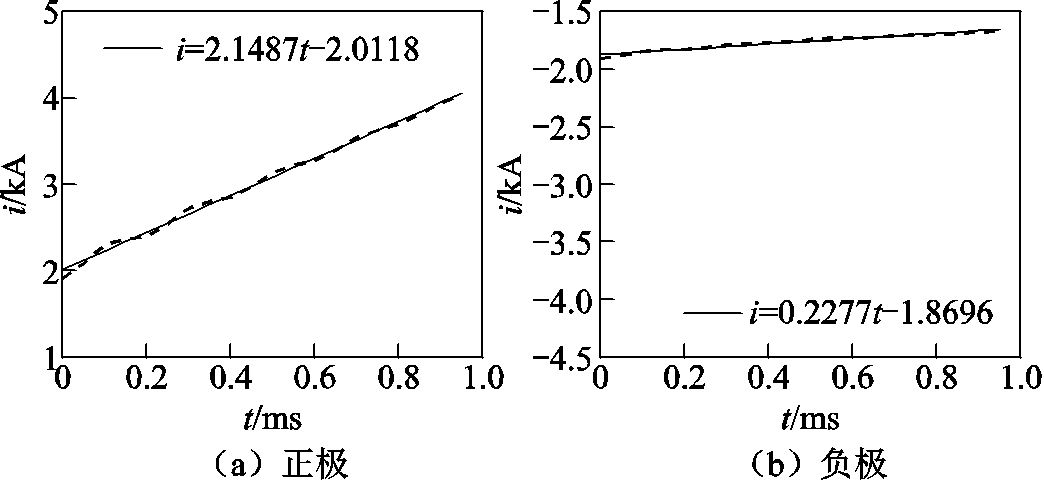
图13 线路1正极故障时正负极电流线性回归曲线及方程
Fig.13 Linear regression curves and equation of positive and negative currents when the positive pole of Line1 failed
线路1发生双极故障时，各线路两端线模电流的线性回归方程及曲线如图14所示，故障线路两端线模电流i14和i41的线性回归方程的回归系数k均为正，对于线路1两端的保护而言，该故障为区内故障；而非故障线路2、3和4两端线模电流的i12和i21、i23和i32、i34和i43的线性回归方程的回归系数k均一正一负，对于线路2、3和4两端的保护而言，该故障为区外故障。
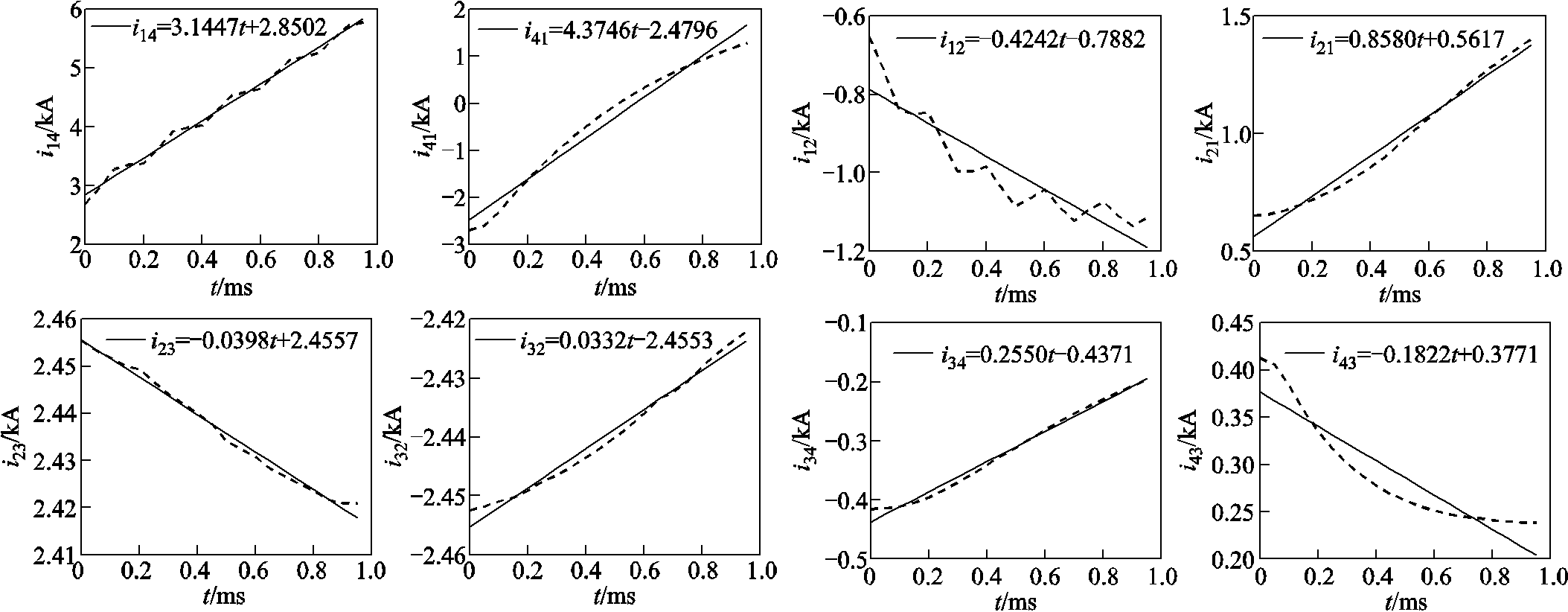
图14 线路1双极故障时各线路两端线模电流的线性回归方程及曲线
Fig.14 Linear regression equation and curves of line mode current at both ends of each line when the bipolar of Line1 failed
线路1双极故障时正负极电流线性回归曲线及方程如图15所示，正极和负极电流经线性回归后的线性函数回归系数分别为2.218 4和-2.228 9，则故障选极参数h 为0.995 3，因此判定为双极故障。
现在同故障位置和不同过渡电阻情况下分别进行仿真对比，利用k值进行故障识别，得到验证结果见表3～表5。
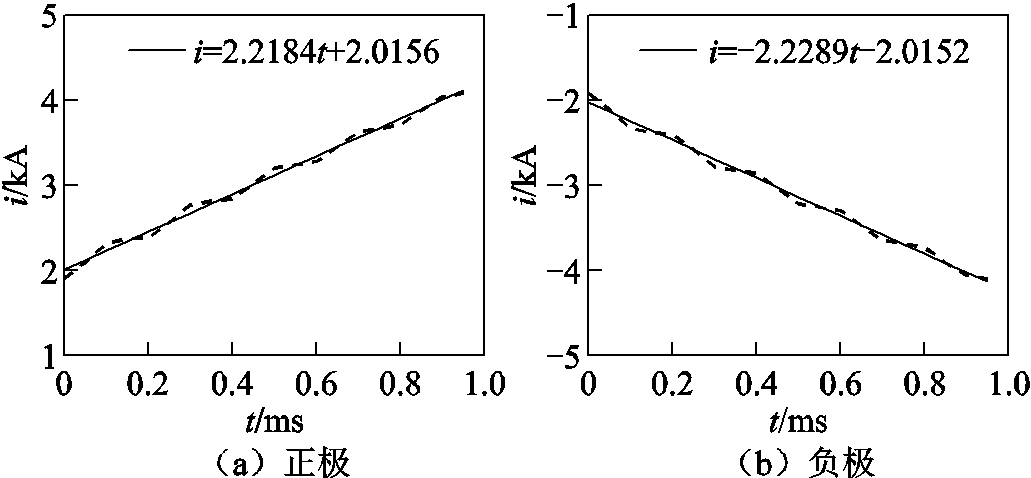
图15 线路1双极故障时正负极电流线性回归曲线及方程
Fig.15 Linear regression curves and equation of positive and negative currents when the bipolar of Line1 failed
表3 不同线路故障的判断结果
Tab.3 Judgment results of different line faults
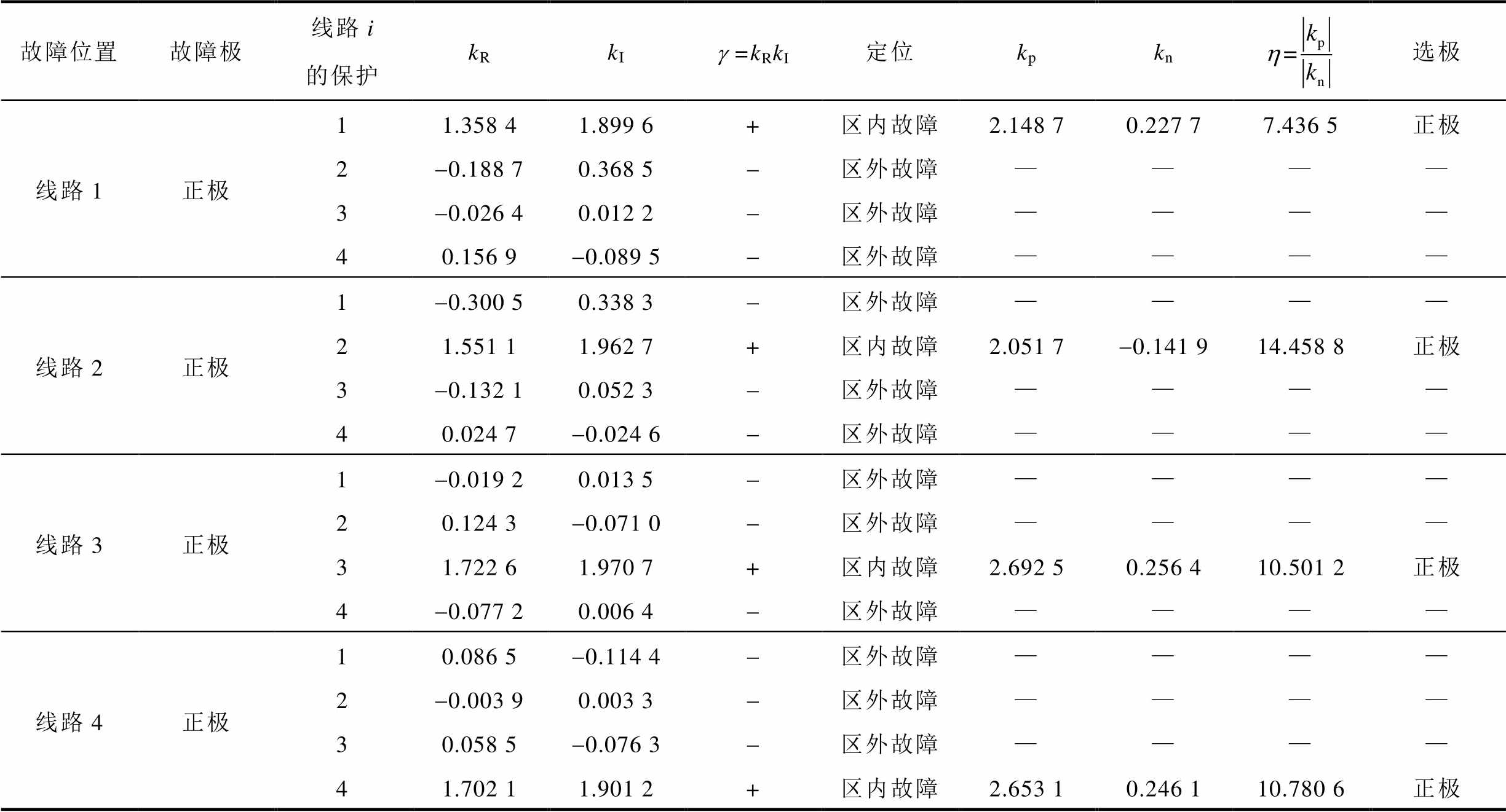
故障位置故障极线路i的保护kRkIg =kRkI定位kpkn选极 线路1正极11.358 41.899 6+区内故障2.148 70.227 77.436 5正极 2-0.188 70.368 5-区外故障———— 3-0.026 40.012 2-区外故障———— 40.156 9-0.089 5-区外故障———— 线路2正极1-0.300 50.338 3-区外故障———— 21.551 11.962 7+区内故障2.051 7-0.141 914.458 8正极 3-0.132 10.052 3-区外故障———— 40.024 7-0.024 6-区外故障———— 线路3正极1-0.019 20.013 5-区外故障———— 20.124 3-0.071 0-区外故障———— 31.722 61.970 7+区内故障2.692 50.256 410.501 2正极 4-0.077 20.006 4-区外故障———— 线路4正极10.086 5-0.114 4-区外故障———— 2-0.003 90.003 3-区外故障———— 30.058 5-0.076 3-区外故障———— 41.702 11.901 2+区内故障2.653 10.246 110.780 6正极
表4 不同故障位置的判断结果
Tab.4 Judgment results for different fault locations
故障位置故障极kRkIg =kRkI定位kpkn选极 首端正极1.358 41.899 6+区内故障2.148 70.227 79.436 5正极 中点1.380 61.589 8+区内故障2.098 40.145 914.382 5正极 末端1.681 71.712 5+区内故障2.369 9-0.008 4282.131 0正极 首端负极1.363 41.885 3+区内故障-0.233 6-2.161 70.108 1负极 中点1.379 31.579 3+区内故障-0.145 0-2.095 60.069 2负极 末端1.678 41.707 9+区内故障0.005 1-2.368 60.002 2负极 首端双极3.144 74.374 6+区内故障2.218 4-2.228 90.995 3双极 中点3.117 23.574 4+区内故障2.199 5-2.208 80.995 8双极 末端3.801 33.883 3+区内故障2.685 8-2.690 00.998 4双极
表5 不同过渡电阻的判断结果
Tab.5 Judgment results of different transition resistances
故障极过渡电阻/WkRkIg =kRkI定位kpkn选极 正极0.011.380 61.589 8+区内故障2.098 40.145 914.382 5正极 1000.954 21.100 6+区内故障1.442 10.092 615.573 4正极 3000.578 70.669 1+区内故障0.873 10.054 615.990 8正极 负极0.011.379 31.579 3+区内故障-0.145 0-2.095 60.069 2负极 1000.950 61.093 0+区内故障-0.095 0-1.439 30.066 0负极 3000.577 80.666 1+区内故障-0.057 1-0.874 20.065 3负极
对各输电线路分别发生正极接地故障、负极接地故障、双极短路故障进行仿真分析，过渡电阻为0.01W，对线路i（i=1, 2, 3, 4）两端的保护来说，线路i发生的故障为区内故障，线路j（j≠i）（j=1, 2, 3, 4）的故障均为区外故障，从表3仿真结果可以看出，无论是哪条线路故障，线路两端的保护均能正确识别。
由表3可知，本文提出的保护方法能识别各条输电线路上的故障。由于篇幅有限，后文仅针对线路1的不同故障位置和不同过渡电阻进行仿真验证。
在线路1的首端、中点和末端分别设置故障来验证本文提出的纵联保护方法，其判定结果见表4。
在本文仿真模型中架空线路均使用的频率相关相域模型，其本质上是分布RLC行波模型，已经考虑了分布电容的影响，因此分布电容不会影响本文所提的纵联保护方法的正确性。
输电线路发生接地故障时，过渡电阻对保护方法的准确性影响很大，为验证该保护方法的耐过渡电阻能力，在线路1距离康保站100km处的单极接地故障时设置了0.01W、100W 和300W 的过渡电阻来验证本文纵联保护方法的正确性，其判定结果见表5。
3.8.1 与基于边界特性的纵联保护对比
本文所提方法不依赖于线路边界，与基于线路边界特性的纵联保护相比，有更好的适应性。
为说明该方法的适应性，现将带有平波电抗器的柔性直流电网与未配置平波电抗器的柔性直流电网进行对比，当线路1正极接地故障时，线路1和线路2的电流原始波形分别如图16a和图16b所示，由图可知，与线路两端配置平波电抗器的输电系统相比，未配置平波电抗器的输电线路故障时，其故障电流的上升速率更快且故障电流峰值更大。
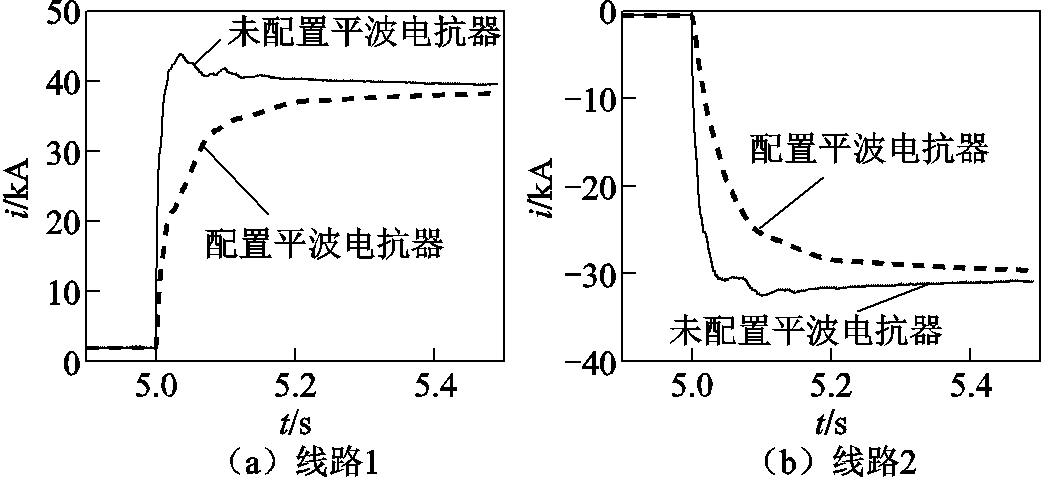
图16 线路1和2的原始电流波形
Fig.16 Original current waveforms of Linel and Line2
计算出两种情况下的回归曲线和回归系数，线路1和线路2的回归曲线分别如图17a和图17b所示，由图可知，与线路两端配置平波电抗器的输电系统相比，未配置平波电抗器的输电线路故障时，其故障电流回归系数更大。
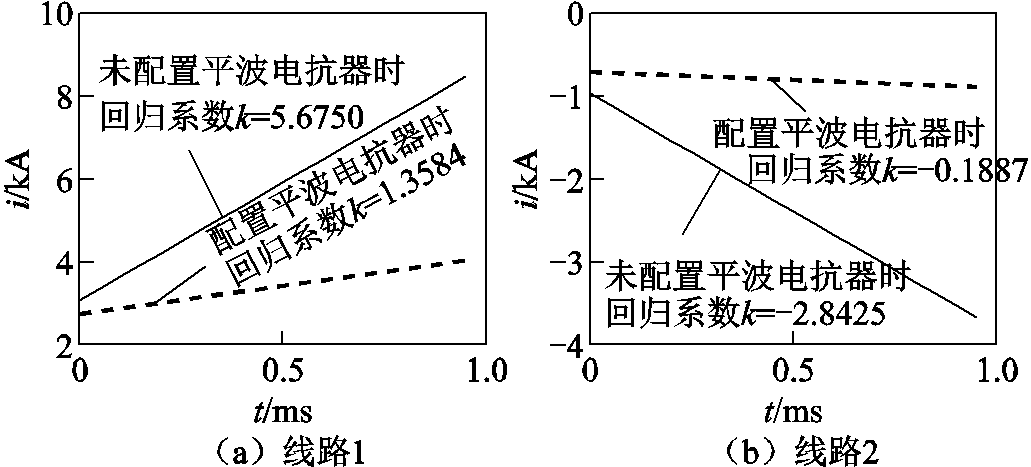
图17 电流回归曲线
Fig.17 Current regression curve
因此，若线路两端没有直流电抗器，则不存在故障识别判据，则该基于边界特性的纵联保护方法失效，而本文方法区分度更好。
3.8.2 与基于电压电流突变量夹角余弦值的方向纵联保护对比
现将该纵联保护方法与本文所提方法进行比较，结果见表6。由表6可知，本文所提方法和基于电压电流突变量夹角余弦值的方法均能正确识别区内故障，当过渡电阻为300W 时，两端电压和电流的夹角余弦值较小，说明电压和电流呈弱相关，则此时的判断结果不可靠，且基于夹角余弦值的纵联保护方法所需数据窗为5ms，而本文方法只需1ms，速动性更好。
表6 与基于电压电流突变量夹角余弦值方法的对比分析
Tab.6 Comparative analysis with the method based on the cosine value of the angle between the voltage and current mutation
故障位置故障极过渡电阻/W本文方法基于电压电流突变量夹角余弦值的方法 kRkI定位定位 线路1正极0.011.380 61.589 8区内故障-0.746 6-0.756 6区内故障 1000.954 21.100 6区内故障-0.534 9-0.585 6区内故障 3000.578 70.669 1区内故障-0.346 1-0.396 8区内故障
本文根据柔性直流电网中输电线路两端故障电流的突变方向以及突变强度，提出了一种柔性直流电网快速纵联保护的线性回归方法，得出以下结论：
1）利用线性回归方法对故障电流进行线性化处理，经分析，线性回归曲线与故障电流曲线有较强的相关性，因此可利用线性回归曲线代替故障电流曲线，进而根据线性回归系数的正负和大小分别进行区内外故障识别和故障选极。
2）本文采用故障后1ms时窗内的暂态信息，保护不受两端控制系统的影响，且该保护方案只需传递正负极性，无需数据同步，降低了保护装置硬件的实现难度。
3）该保护方法不依赖于线路边界，耐受过渡电阻能力强，可靠性高。
参考文献
[1] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J/OL]. 电工技术学报: 1-17[2022-04-02]. DOI: 10.19595/j.cnki. 1000-6753.tces.211730.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J/OL]. Transactions of China Electrotechnical Society: 1-17[2022-04-02]. DOI: 10.19595/j.cnki.1000- 6753.tces. 211730.
[2] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835.
Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dis- patching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[3] 刘振亚. 全球能源互联网跨国跨洲互联研究及展望[J]. 中国电机工程学报, 2016, 36(19): 5103-5110.
Liu Zhenya. Research of global clean energy resource and power grid interconnection[J]. Proceedings of the CSEE, 2016, 36(19): 5103-5110.
[4] Zhu Fahua, Zheng Youfei, Guo Xulin, et al. Environ- mental impacts and benefits of regional power grid interconnections for China[J]. Energy Policy, 2005, 33(14): 1797-1805.
[5] 徐政, 刘高任, 张哲任. 柔性直流输电网的故障保护原理研究[J]. 高电压技术, 2017, 43(1): 1-8.
Xu Zheng, Liu Gaoren, Zhang Zheren. Research on fault protection principle of DC grids[J]. High Voltage Engineering, 2017, 43(1): 1-8.
[6] 付华, 陈浩轩, 李秀菊, 等. 含边界元件的MMC-MTDC直流侧单端量故障辨识方法[J]. 电工技术学报, 2021, 36(01): 215-226.
Fu Hua, Chen Haoxuan, Li Xiuju, et al. MMC-MTDC DC side single-ended quantity fault identification method with boundary elements[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 215-226.
[7] 郭贤珊, 周杨, 梅念, 等. 张北柔性直流电网故障电流特性及抑制方法研究[J]. 中国电机工程学报, 2018, 38(18): 5438-5446.
Guo Xianshan, Zhou Yang, Mei Nian, et al. Research on the fault current characteristic and suppression strategy of Zhangbei project[J]. Proceedings of the CSEE, 2018, 38(18): 5438-5446.
[8] 汤广福, 王高勇, 贺之渊, 等. 张北500kV直流电网关键技术与设备研究[J]. 高电压技术, 2018, 44(7): 2097-2106.
Tang Guangfu, Wang Gaoyong, He Zhiyuan, et al. Research on key technology and equipment for Zhangbei 500kV DC grid[J]. High Voltage Engineering, 2018, 44(7): 2097-2106.
[9] 束洪春, 代月, 安娜, 等. 基于交叉重叠差分变换的MMC-HVDC线路故障识别方法[J]. 电工技术学报, 2021, 36(1): 203-214, 226.
Shu Hongchun, Dai Yue, An Na, et al. Fault identification method of MMC-HVDC line based on sequential overlapping derivative transform[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 203-214, 226.
[10] 宁连营, 邰能灵, 郑晓冬, 等. 基于自定义差分电流的MMC-HVDC输电线路纵联保护[J]. 电力系统自动化, 2017, 41(17): 87-93, 133.
Ning Lianying, Tai Nengling, Zheng Xiaodong, et al. Harmonic resonance analysis and suppression method for transmission cables between renewable energy sources and power grid[J]. Automation of Electric Power Systems, 2017, 41(17): 87-93, 133.
[11] 周光阳, 李妍, 何大瑞, 等. 含限流器的多端柔直系统故障保护策略[J]. 电工技术学报, 2020, 35(7): 1432-1443.
Zhou Guangyang, Li Yan, He Darui, et al. Protection scheme for VSC-MTDC system with fault current limiter[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1432-1443.
[12] 王帅, 毕天姝, 贾科. 基于小波时间熵的MMC- HVDC架空线路单极接地故障检测方法[J]. 电网技术, 2016, 40(7): 2179-2185.
Wang Shuai, Bi Tianshu, Jia Ke. Wavelet entropy based single pole grounding fault detection approach for MMC-HVDC overhead lines[J]. Power System Technology, 2016, 40(7): 2179-2185.
[13] Zhang Shuo, Zou Guibin, Wang Chuanjie, et al. A non-unit boundary protection of DC line for MMC- MTDC grids[J]. International Journal of Electrical Power & Energy Systems, 2020, 116: 105538.
[14] Tang Lanxi, Dong Xinzhou, Shi Shenxing, et al. A high-speed protection scheme for the DC transmission line of a MMC-HVDC grid[J]. Electric Power Systems Research, 2019, 168: 81-91.
[15] 周家培, 赵成勇, 李承昱, 等. 采用电流突变量夹角余弦的直流电网线路纵联保护方法[J]. 电力系统自动化, 2018, 42(14): 165-171.
Zhou Jiapei, Zhao Chengyong, Li Chengyu, et al. Pilot protection method for DC grid lines based on included angle cosine of fault current component[J]. Automation of Electric Power Systems, 2018, 42(14): 165-171.
[16] 姚为正, 行登江, 吴金龙, 等. 柔性直流电网超高速保护方案研究[J].电网技术, 2017, 41(6): 1710- 1718.
Yao Weizheng, Xing Dengjiang, Wu Jinlong, et al. Study on ultra-high-speed protection method of flexible HVDC grid[J]. Power System Technology, 2017, 41(6): 1710-1718.
[17] 汤兰西, 董新洲, 施慎行, 等. 柔性直流电网线路超高速行波保护原理与实现[J]. 电网技术, 2018, 42(10): 3176-3186.
Tang Lanxi, Dong Xinzhou, Shi Shenxing, et al. Principle and implementation of ultra-high-speed travelling wave based protection for transmission line of flexible HVDC grid[J]. Power System Technology, 2018, 42(10): 3176-3186.
[18] 何佳伟, 李斌, 李晔, 等. 多端柔性直流电网快速方向纵联保护方案[J]. 中国电机工程学报, 2017, 37(23): 6878-6887, 7078.
He Jiawei, Li Bin, Li Ye, et al. A fast directional pilot protection scheme for the MMC-based MTDC grid[J]. Proceedings of the CSEE, 2017, 37 (23): 6878-6887, 7078.
[19] 宋国兵, 侯俊杰, 郭冰. 基于主动探测式的柔性直流电网纵联保护[J]. 电网技术, 2020, 44(10): 4001- 4010.
Song Guobing, Hou Junjie, Guo Bing. Pilot protection of flexible DC grid based on active detection[J]. Power System Technology, 2020, 44(10): 4001-4010.
[20] 董新洲, 汤兰西, 施慎行, 等. 柔性直流输电网线路保护配置方案[J]. 电网技术, 2018, 42(6): 1752-1759.
Dong Xinzhou, Tang Lanxi, Shi Shenxing, et al. Configuration scheme of transmission line protection for flexible HVDC grid[J]. Power System Technology, 2018, 42(6): 1752-1759.
[21] 牛洪波. 线性回归在“工业分析检验”竞赛选手选拔中的应用[J]. 烟台职业学院学报, 2018, 24(4): 86-92.
Niu Hongbo. Application of linear regression in the selection of contestants in "industrial analysis and inspection"[J]. Journal of Yantai Vocational College, 2018, 24(4): 86-92.
[22] 孙秀. 改进的贝叶斯方法在设备故障检测中的应用[D]. 济南: 齐鲁工业大学, 2018.
Pilot Protection Method of Flexible DC Grid Based on Linear Regression
Abstract When a fault occurs in a flexible DC grid line, the line protection device needs to quickly and reliably remove the faulty line to ensure that the healthy line can operate normally to improve the safety and reliability of the transmission system. In this paper, a linear regression method for fast pilot protection of flexible DC grid is proposed. Firstly, the physical boundary formed by the modular multilevel converter (MMC) equivalent impedance and the smoothing reactor is analyzed for the attenuation of the high frequency components, and secondly, the current loop and the current flow of the healthy line are analyzed for the single-pole and double-pole faults of the transmission line, and then the regression coefficient of the short-time window current is used for the identification of faults inside and outside the area and the selection of the faulted pole according to the energy of the voltage mutation of the transmission line as the protection activation criterion. A simulation model of the flexible DC network is built on PSCAD to verify the protection scheme. The simulation results show that the protection method can reliably and accurately screen faults with good quick action, and has good transition resistance and applicability.
keywords：Flexible DC grid, modular multilevel converter (MMC) physical boundary, linear regression, fault detection, line protection
DOI:10.19595/j.cnki.1000-6753.tces.210969
中图分类号：TM723
束洪春 男，1961年生，博士，教授，博士生导师，研究方向为电力系统新型继电保护与故障测距、故障录波、数字信号处理及DSP应用等。E-mail：kmshc@sina.com.cn
代 月 女，1995年生，博士研究生，研究方向为高压直流输电与柔性交流输电技术。E-mail：1769624266@qq.com（通信作者）
收稿日期 2021-07-02
改稿日期 2021-09-10
国家自然科学基金（52037003）和云南省重大专项（202002AF080001）资助项目。
（编辑 郭丽军）