0 引言
近年来,气候变化导致极端自然灾害发生的频率和强度增大,由此造成的大规模停电事故也随之增多[1]。大停电后的电力系统恢复通常分为黑启动、网架重构和负荷恢复三个阶段[2-3]。其中,负荷恢复是电力系统恢复的最终目标。负荷恢复期间,受系统各类安全约束影响,变电站单次恢复的负荷量应小于最大可恢复负荷量。随着社会经济的发展,以空调为代表的温控负荷占比逐年增加。据统计,在城市居民用电中,空调负荷在高峰时段占比达到30%~40%,局部区域甚至超过50% [4]。停电后直接进行负荷恢复,空调负荷的冷启动特性可能导致负荷量超出系统的承受能力。因此,充分发挥空调负荷的需求响应潜力,研究变电站负荷恢复量的削减方法对负荷恢复具有重要的实际意义。
除大停电场景外,限电场景下的负荷恢复研究亦具有现实意义。2020 年8 月14、15 日,美国加州发生轮流停电事件[5-6]。极端天气所导致的空调负荷需求激增,并且电力系统可提供的恢复功率有限,进一步加大了系统供需矛盾。在后续的负荷恢复中,则存在启动空调负荷所带来的负荷量激增的问题,需要合理手段削减负荷恢复量,满足系统的可承受能力,保证负荷恢复顺利进行。
针对大停电后的负荷恢复问题,国内外进行了大量的研究[7-8]。由于空调负荷占比的不断提升,考虑冷负荷启动特性的负荷恢复量计算得到了重点关注。文献[9]考虑冷负荷的启动特性以及各种约束条件,通过粒子群算法确定系统最优负荷恢复位置与最大负荷恢复量。文献[10]使用线性化技术构建了一个通用频率估算模型,可快速计算冷负荷启动后的系统频率动态特性。文献[11]应用多状态负荷模型计算冷负荷启动的峰值和持续时间。文献[12]量化了温控负荷多样性水平、环境温度、停电时间三个因素对冷负荷过载系数和持续时间的影响。上述研究对于冷负荷恢复量计算具有较高参考价值,但缺乏一种适应于不同停电场景的冷负荷启动量计算方法,此外,相关研究均未考虑限电场景下的负荷恢复问题。空调负荷作为潜力巨大的需求响应资源,其负荷削减潜力已经得到广泛关注。文献[13]提出了一种采用居民负荷控制技术抑制微电网联络线功率波动的方法。文献[14]提出一种基于负荷响应的多智能体主从一致性分散协调算法,可用于大规模空调参与的系统调峰。文献[15]考虑空调负荷削减 能力的不确定性,对故障后所形成孤岛网络的最大运行时长进行预估。因此,空调负荷需求响应技术可以用于削减停电场景下的负荷恢复量,但目前仍缺乏相关研究。
针对空调负荷冷负荷启动特性,本文提出了一种考虑空调负荷需求响应的负荷恢复量削减方法。首先,建立计及停电时间的空调负荷群聚合功率估计模型;然后,综合考虑暂态安全约束及系统可提供的恢复功率,确定变电站单次可恢复负荷量的最大限值;最后,基于空调负荷群聚合功率估计模型和变电站单次可恢复负荷量限值,利用空调负荷控制技术削减超出的负荷量,保证负荷恢复顺利进行。
1 故障后负荷恢复量计算方法
为了分析空调负荷的冷负荷特性,考虑停电时间、温度设定值等影响因素,推导了空调负荷聚合功率估计模型,并基于此模型,计算变电站故障后的负荷恢复量。
1.1 空调负荷聚合功率估计模型
为估算空调负荷群聚合功率,首先推导室内温度变化与功率的关系。本文以定频制冷空调为研究对象,所得相关结论可以推广应用到制热空调模型中[16]。一阶等效热参数模型所用参数较少,在忽略一定因素的情况下,可以更集中地处理功率与温度的关系,在国内外相关研究中被广泛应用[17]。首先,采用一阶常微分方程来描述室内温度的变化,即[18]
式中,θ(t)为t 时刻的室内温度;θout 为室外温度;R为等效热阻;C 为等效热容;Pc 为空调负荷的制冷功率,制冷功率Pc 与额定功率P 满足Pc=ηP,η 为能效比;s(t)为开关状态,取值为“0”或“1”,分别表示关闭或开启运行状态。
空调负荷开关状态与空调设定温度和室内温度相关。图1 为空调制冷工况下开关切换示意图。其中,温度设定值与室内温度上、下限的关系为
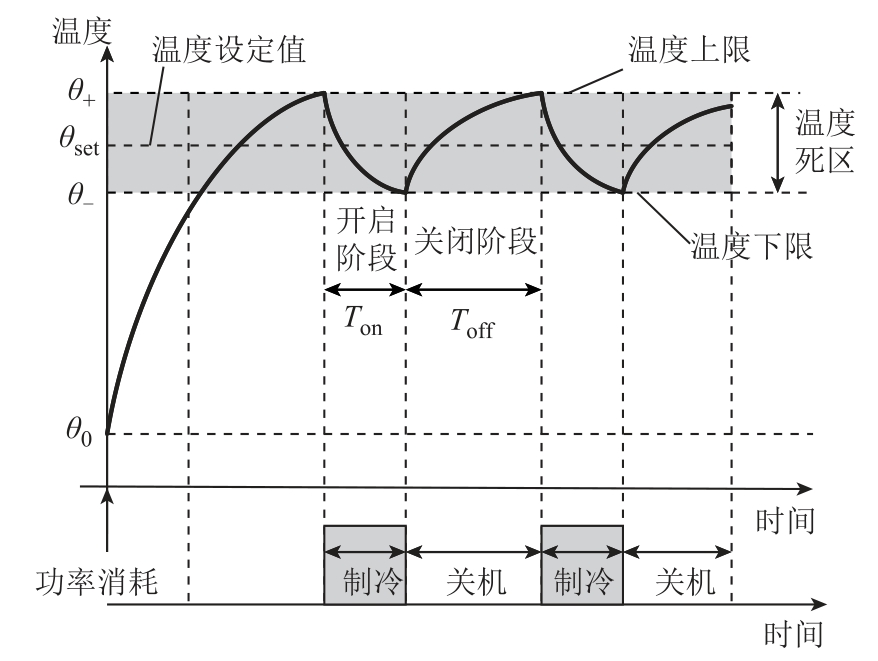
图1 空调制冷工况开关切换示意图
Fig.1 Switching condition of the air-conditioning in cooling mode
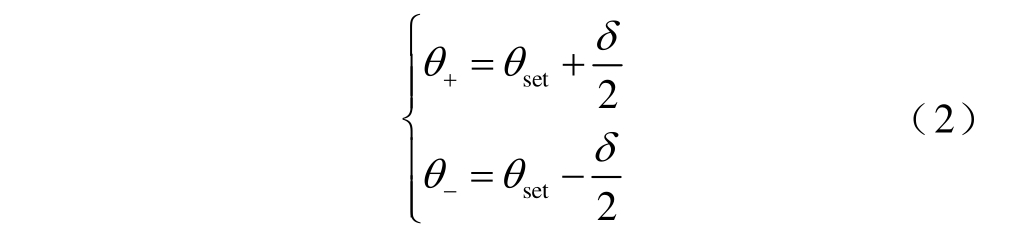
式中,θ+和θ-分别为切换开关状态时的室内温度上、下限值;θset 为空调的温度设定值;δ 为温度死区。
根据式(1)和式(2),求解单台空调开、停机时间为
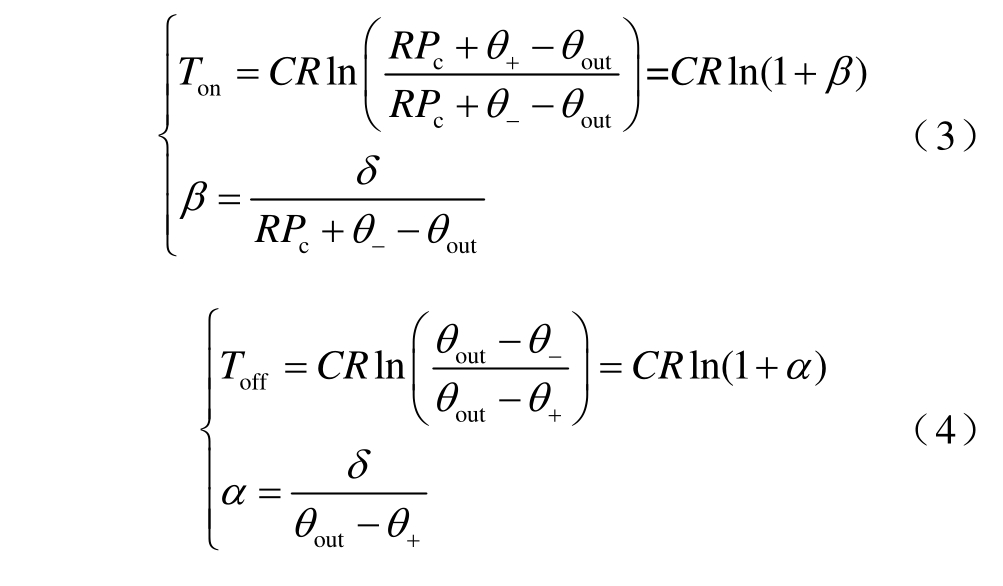
式中,Ton 为开机时间;Toff 为停机时间。
在稳态时,第i 个空调处于开机状态的概率与其占空比(开启时间占整个运行时间的比重)的关系为[16]
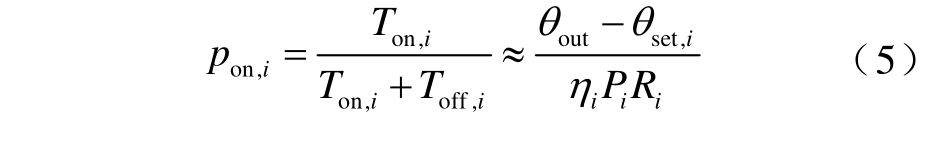
式中,pon,i 为第i 个空调的开机状态概率;η 为空调ii 的能效比;Pi 为空调i 的额功率;Ri 为空调i 的等效热阻。
停电发生后,所有空调被迫处于关闭状态,经过停电时间T0 后恢复供电。考虑最严重的情况,即马上开启全部空调,计算结果偏保守,对负荷恢复来说是可以接受的。室内温度若已经超过温度切换值上限θ+,则pon,i 为1;若仍然处于温度区间内,会按照停电之前状态运行。此时第i 个空调处于开机状态的概率为
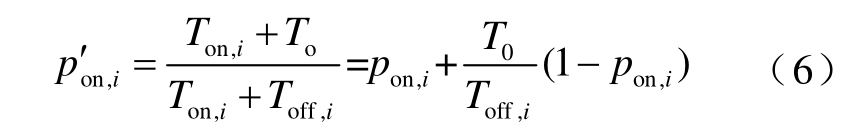
式中,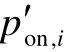 为停电后第i 个空调的开机状态概率;
为停电后第i 个空调的开机状态概率;![]() 。
。
空调群聚合功率与此时处于开机状态的数量成正比。当空调数量足够大且相互独立运行时,由大数定律可得
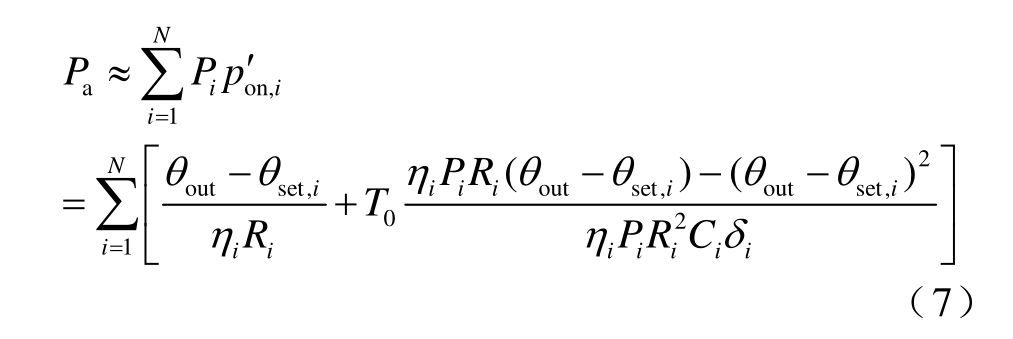
式中,Pa 为N 个空调的聚合功率;![]() 。
。
由此可以看出,空调负荷的聚合功率除了与自身热特性参数有关,更受到停电时间的影响。停电时间通过影响空调开机状态的概率而影响空调聚合功率的大小。在一定停电时间内,聚合功率与停电时间为正比关系,达到一定时间后,即使停电时间再增加也保持不变。
1.2 故障后负荷恢复量
故障后实际恢复的负荷量通常可以分为温控负荷和固定负荷两类。其中,固定负荷在停电前后变化幅度不大,而温控负荷在恢复时接入的总容量较故障前增大很多。温控负荷主要包含空调负荷、冰箱、加热器等。在夏季和冬季的用电高峰,空调负荷是温控负荷的重要部分和需求响应中负荷量削减的控制对象,本文采用空调负荷代表温控负荷进行研究。
温控负荷冷负荷启动的冲击由两部分组成:负荷多样性缺失造成的负荷恢复量增加和负荷冷启动时的冲击电流[2]。前者可通过上述空调负荷聚合功率估计模型予以计算;后者主要由电动机起动时的冲击造成,在负荷投入时通过计算暂态电压跌落予以考虑。本节重点关注恢复时负荷点的初始负荷量大小,供电恢复时变电站的负荷量可以表示为
式中,PS 为恢复时变电站的负荷恢复量;PF 为固定负荷恢复量;PT 为恢复时温控负荷恢复量。
2 变电站最大可恢复负荷量
2.1 变电站负荷恢复能力计算模型
大停电后若单次负荷投入量过大可能会引起电压、频率跌落问题。为计算单次能够恢复的最大负荷量,建立了变电站负荷恢复能力模型,目标函数为
式中,Pz 为变电站单次恢复的负荷量。
同时,需综合考虑电压、频率等多种约束,具体如下。
1)电压约束
恢复控制中,电压必须保持在规程允许范围内。电压约束包括稳态电压约束和暂态电压约束。稳态电压Vu,st 可以通过相应负荷量下的系统稳态潮流进行计算,其稳态电压为
式中,J 为节点总数;Vmax 和Vmin 分别为稳态电压上、下限。
负荷投入的初始冲击可能会引起严重的暂态电压下降,尤其是负荷中电动机的起动过程,暂态电压响应速度一般要快于频率的响应过程。因此必须重点考虑暂态电压安全约束。暂态电压约束的判据为电压低于设定值的时间不能超过设定时间[2],该约束可表示为
式中,Vset 为电压设定值;tset 为时间设定值;T 为节点电压Vu 低于电压设定值Vset 的时间,其值可根据文献[19]所提方法进行计算。
2)频率约束
恢复控制过程中发电机组的频率响应是决定负荷恢复量大小的关键[20-21]。给定负荷恢复量所引起的系统频率偏移超过一定范围,将可能引起低频减载动作甚至导致稳定性破坏的后果。由此,系统频率约束可以表示为
式中,Δfmax 和Δfmin 分别为系统频率偏差的上、下限。
本文采用典型的原动机频率响应率,估算给定负荷恢复量下系统的最大频率偏移为
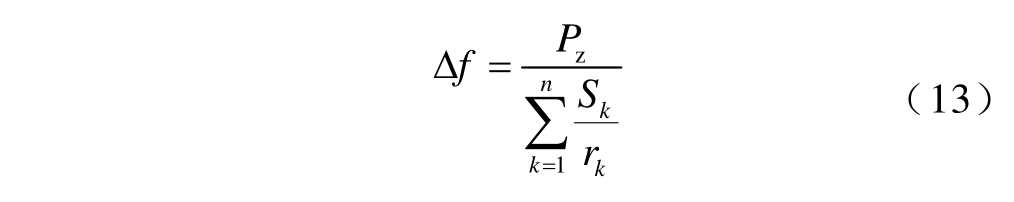
式中,kS 为已恢复机组k 的额定容量;rk 为已恢复机组k 的频率响应率。
2.2 模型求解
上述模型可以通过线性搜索算法求解,二分法作为常用的一维线性搜索算法,其计算过程简单,方法可靠,具有良好的收敛性,本文采用此方法求解上述优化问题。首先初始化负荷搜索范围,并得到初始待校验负荷量,迭代过程中根据校验是否成功更新负荷量取值的下限或上限,取该范围的中点作为新的负荷量继续迭代,直至满足收敛条件。
采用二分法对变电站负荷恢复能力计算模型进行求解的主要步骤如下:
1)初始化负荷搜索范围,确定上限Pzmax 和下限Pzmin,并取该范围中点为待校验负荷量Pznew。
2)对待校验负荷量Pznew 的频率与电压约束进行校验。
3)若约束全部满足,则将当前迭代中的负荷量Pznew 作为下次迭代中负荷量范围下限Pzmin;反之作为负荷量范围上限Pzmax,调整后范围的中点作为下次迭代的待校验负荷量Pznew。
4)判断是否满足Pzmax-Pzmin<ε(ε 为很小正数),如是,待校验负荷量为最优值;否则,返回步骤2)。
2.3 变电站最大可恢复负荷量
在大停电场景下,变电站最大可恢复负荷量根据2.1 节模型求得。在限电场景下的负荷恢复中,系统可提供的恢复功率有限,其值可能低于变电站的恢复能力。综合考虑不同停电场景,变电站最大可恢复负荷量为
式中,Pm 为变电站最大可恢复负荷量;PL 为变电站单次能够恢复的最大负荷量;PA 为系统可提供恢复功率。
3 负荷恢复量削减方法
空调负荷由于冷负荷启动特性会产生远超过稳态的聚合功率,在空调负荷占比高的系统中,停电后如果直接进行负荷恢复,可能超过系统允许的最大可恢复负荷量。尤其在限电场景下的负荷恢复中,系统可提供的恢复功率有限。为保证不同停电场景下负荷恢复量均在最大限值之内,需要发挥需求响应潜力,削减超出限值的负荷量,以确保负荷恢复顺利进行。
3.1 负荷恢复需求响应控制算法
需求响应从用户参与方式上分为直接对用户负荷设备进行控制的可调度需求响应和需要用户参与的可选择需求响应。可调度需求响应获得用户负荷设备的控制授权,更为快速可靠。在负荷恢复场景下,可调度需求响应能够快速准确地掌握控制后的负荷量。本文设定用户已经签订合适的协议,空调在经过必要改装后开关状态能够配合需求响应方案的实施。
现有研究中空调运行控制策略主要有温度控制和开关控制两种。温度控制策略通过改变温度设定值调整空调启停数量,随机性和波动性较强。对负荷恢复场景来说,开关控制策略能够快速便捷地实现负荷量削减目标。空调关闭顺序由恢复供电时的温度相对位置来决定,即温度相对靠近温度区间的空调关闭优先级高。引入状态特征量H(t)来表示空调的温度状态[15]。
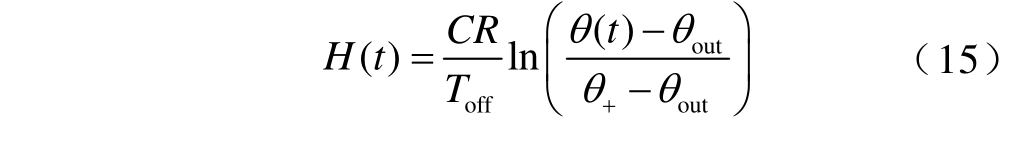
H(t)用空调负荷到达温度上限的时间与停机时间的比值表示,体现了t 时刻温度的相对位置。在温度区间内温度的变化可以看作是线性化过程,室内温度上升速度(θ+–θ-)/Toff 保持不变[16],则式(15)可以化简为
H(t)越大,此时温度距离温度下限越近,则相同设定温度下关闭此空调的优先级越高。空调负荷首先按照H(t)降序排序,相同的H(t)按照设定温度θset 由低到高排序,关闭顺序从H(t)最大值中设定温度最低开始,依次关闭M 台空调负荷直到满足式(17),即在保证系统安全的前提下尽快、尽可能多地恢复负荷。
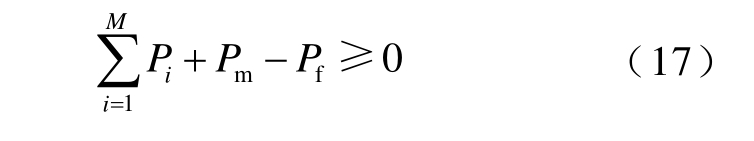
对空调的制热状态,H(t)的计算公式可按式(18)进行修改。此时,H(t)值越大表示温度距离温度上限越近,空调关闭顺序的优先级越高。
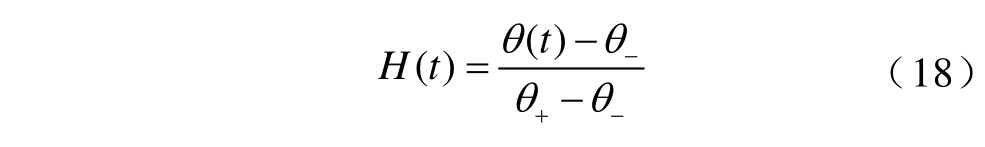
3.2 负荷恢复量削减方法流程
通过负荷恢复量削减方法可保证负荷恢复可靠进行,其流程如图2 所示。
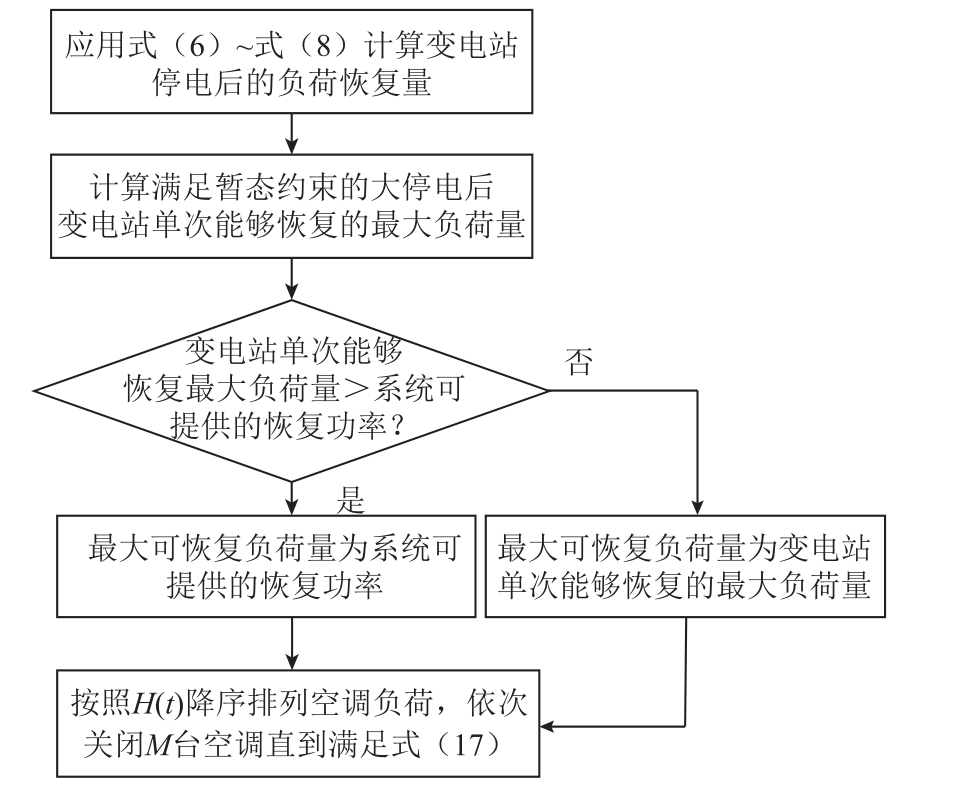
图2 负荷恢复量削减方法流程
Fig.2 Flow chart of load restoration amount reduction method
负荷恢复量削减方法具体流程如下:
1)计算停电后的负荷恢复量。根据变电站负荷占比、温控负荷参数以及停电时间,计算停电一段时间后的负荷恢复量。
2)计算变电站负荷恢复能力。通过求解考虑频率与电压约束的变电站负荷恢复能力模型确定变电站单次能够恢复的最大负荷量。
3)确定变电站单次最大可恢复负荷量。比较变电站单次能够恢复的最大负荷量与系统可提供的恢复功率的大小,变电站单次最大可恢复负荷量为两者较小值。
4)负荷恢复量削减。对空调负荷按照H(t)降序依次关闭M 台空调负荷直到式(17)成立,实现在保证系统安全的前提下尽快、尽可能多地恢复负荷。
4 算例分析
4.1 聚合功率估计模型验证
为了说明所提空调负荷聚合功率计算模型的有效性,将其与蒙特卡洛模拟法进行对比。空调负荷参数见表1。假设由1 000 台可控空调组成空调群,热阻、热容、制冷功率服从对数正态分布,空调参数在取值区间内抽样得到[22-23],空调初始开关状态随机选择。因为蒙特卡洛模拟法是目前大多数文献中分析空调负荷群运行特性时普遍采用的方法[23],对每一个空调按照式(1)模拟空调运行轨迹,计算一定停电时间后空调温度情况,在供电恢复时刻判断空调状态,对负荷群中所有空调进行抽样模拟,即可得到整个空调负荷群的蒙特卡洛模拟,将其计算结果作为比较的基准值。
表1 空调负荷参数
Tab.1 Air conditioning parameters

分别用本文所提空调聚合功率估计模型和通用的蒙特卡洛方法,计算不同停电时间和外界温度条件下的空调负荷聚合功率,结果如图3 所示。由图3 可以看出,随着停电时间的增加空调聚合功率先是不断增加,近似呈现正比关系,然后稳定在最大值不变。外界温度越高,空调稳态聚合功率越大,聚合功率上升速度加快,到达最大聚合功率值的停电时间变短。
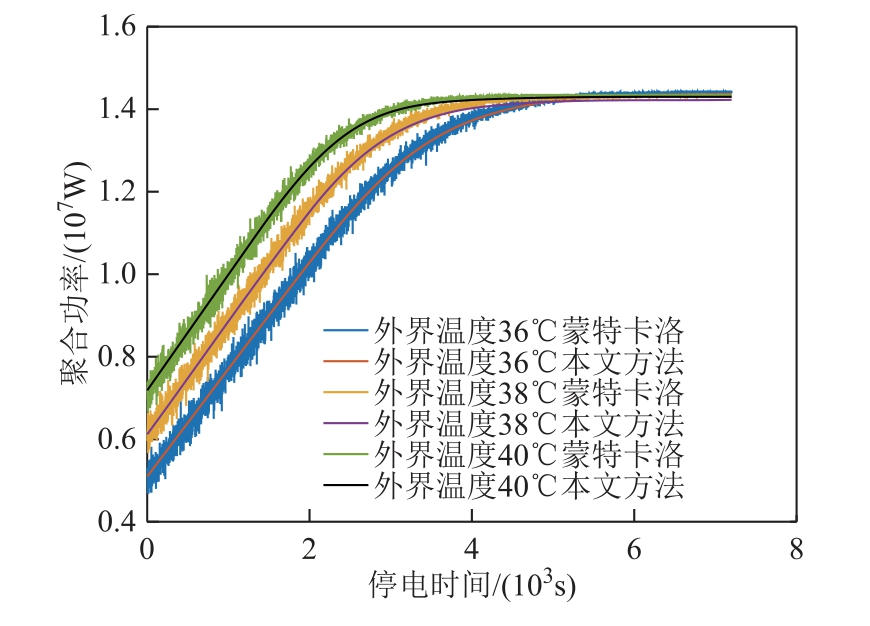
图3 空调聚合功率与停电时间和外界温度的关系
Fig.3 The air-conditioning loads aggregated power in relation to outage time under different ambient temperature
为了更直观地展示所提空调负荷聚合功率估计模型的估算误差,在不同停电时间和外界温度下,以蒙特卡洛模拟法所得空调聚合功率作为基准值,计算所提方法的相对误差,如图4 所示。由图4 可以看出,随着停电时间的增加,相对误差逐渐缩小。并且,外界温度越高,相对误差越小。

图4 空调聚合功率评估相对误差与停电时间和外界温度的关系
Fig.4 The relationship between the air-conditioning loads aggregated power estimation relative error and outage time under different ambient temperature
4.2 IEEE 14 节点算例
为验证所提负荷恢复量削减方法的有效性,采用如图5 所示的IEEE 14 节点系统进行仿真验证。假定1 号、2 号、3 号机组为水轮机组,具有黑启动能力,容量均为100MV·A。6 号和8 号机组为汽轮机组,8 号机组容量为350MV·A。系统发生大停电后,区域1 首先形成稳定小系统,其初始负荷水平为120MW,经过节点7 起动8 号机组。8 号机组在并网后,通过线路9-14 恢复节点14 的负荷。假设空调负荷中电动机和阻抗占比为6.5∶3.5,固定负荷为4:6,各负荷类型的电动机模型均采用同一参数[19]。频率偏差在±0.5Hz 内,稳态电压在0.9(pu)~1.1(pu)范围,暂态电压约束的电压设定值为0.8(pu),时间设定值为0.5s。
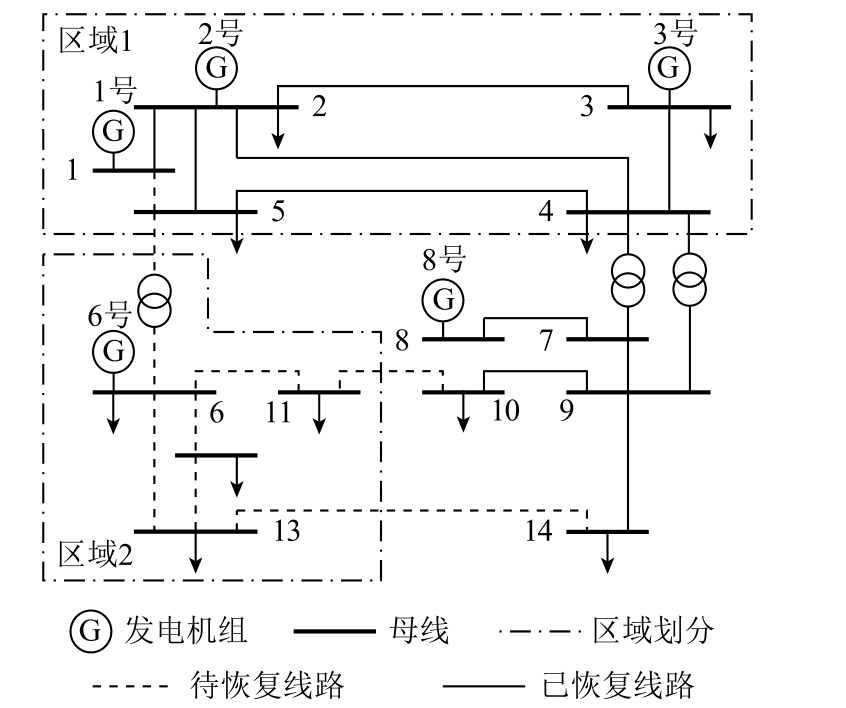
图5 IEEE 14 节点系统
Fig.5 IEEE 14-bus sysytem
4.2.1 参数变化对负荷恢复量的影响
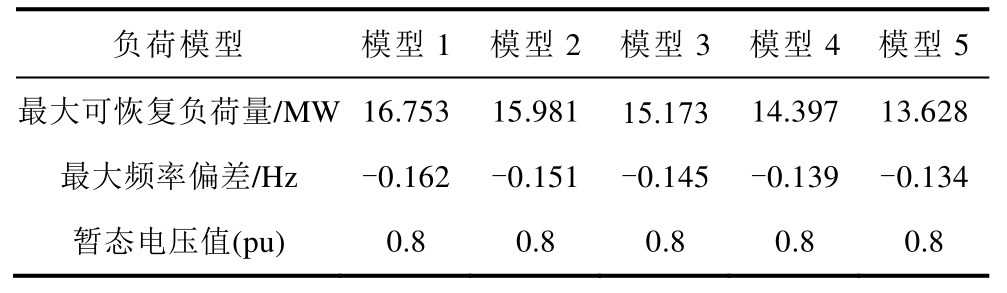
为了说明负荷组成对负荷恢复量的影响,首先分别计算节点14 在以下几个模型下的最大可恢复负荷量。模型1 代表温控负荷20%+固定负荷80%;模型2 代表温控负荷30%+固定负荷70%;模型3代表温控负荷40%+固定负荷60%;模型4 代表温控负荷50%+固定负荷50%;模型5 代表温控负荷60%+固定负荷40%。空调负荷参数取值见表1,计算结果见表2。优化过程中,针对暂态电压约束和频率约束,分别采用式(11)~式(13)进行校验。由结果可以看出,随着温控负荷占比的增加,系统最大可恢复负荷量逐渐减少,且最大可恢复负荷量主要受到暂态电压约束的影响。
表2 节点14 不同负荷模型下的最大可恢复负荷量
Tab.2 Maximum restorable load amounts with different load structures at Bus 14
负荷恢复量与停电时间(从故障停电到恢复供电的时间)和负荷组成有关,随停电时间的增加而增加,直到达到最大值,即最大负荷恢复量。定义越限时间为当负荷恢复量等于最大可恢复负荷量时的停电时间。停电时间超过越限时间,则需要实施需求响应策略关闭相应数量的空调负荷。负荷恢复量在不同负荷组成下的计算结果见表3。当温控负荷占比较低,最大负荷恢复量不会超过最大可恢复负荷量,无需实施需求响应策略。温控负荷占比高时,停电时间超过越限时间,负荷恢复量会超过最大可恢复负荷量,需要关闭一定数量的空调负荷。随着系统温控负荷占比的增加,越限时间逐渐减少,参与需求响应控制的空调数量逐渐增加。在温控负荷占比高的系统中,停电较短时间负荷量就会超出系统安全约束,需求响应潜力应该得到充分利用。
表3 节点14 不同负荷模型下的负荷恢复量
Tab.3 Load restoration amounts with different load structures at Bus 14
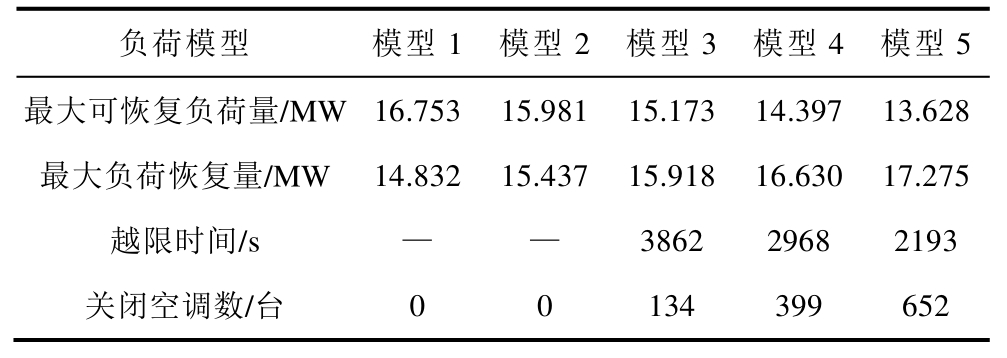
注:最大可恢复负荷量表示满足频率与电压约束条件下单次能够恢复的最大负荷量;最大负荷恢复量表示停电时间足够长的负荷恢复量;越限时间表示负荷恢复量等于最大可恢复负荷量对应的停电时间;关闭空调数表示最大负荷恢复量削减到最大可恢复负荷量需关闭的空调台数。
为了说明外界温度变化对负荷恢复量的影响,选取节点14 的模型4,分别计算外界温度从32℃变化到41℃时的越限时间,结果如图6 所示。在负荷组成不变的情况下,最大可恢复负荷量和最大负 荷量保持不变。从图6 中可以看出,越限时间随温度升高逐渐减少,在33℃时需要停电大约1.5h 实际负荷量才能达到最大可恢复负荷量,在41℃就只需要大约0.5h。在夏季高温天气下,较短的停电时间就会使得实际负荷量超过系统约束,此时需要充分发挥需求响应削负荷潜力。
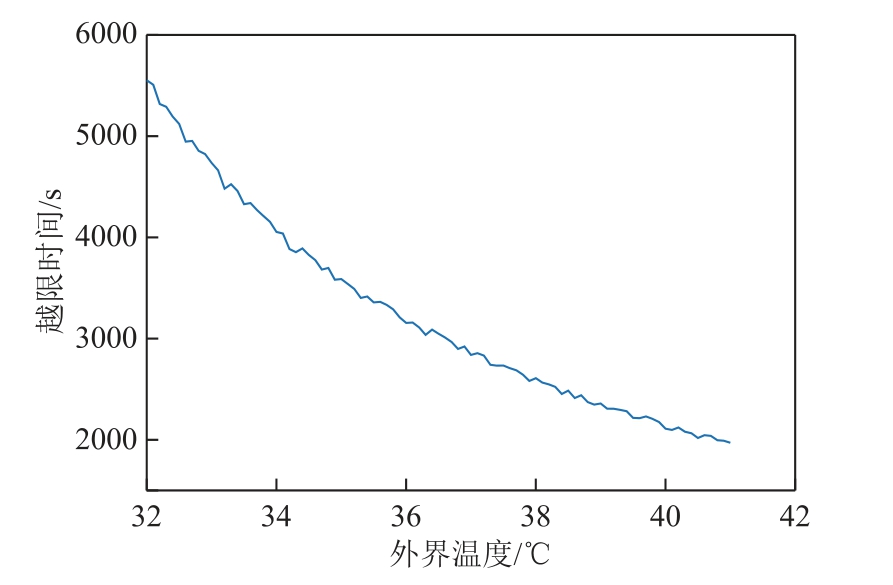
图6 越限时间与外界温度的关系
Fig.6 The relationship between the over-limit time and ambient temperature
4.2.2 考虑限电场景的负荷恢复量削减
加州停电事件说明,限电场景下的负荷恢复问题也要予以考虑。考虑到限电的情况,最大可恢复负荷量为变电站单次能够恢复最大负荷量和系统可提供恢复功率的较小值。
随着停电时间增加,负荷恢复量会超过系统上限,需要通过关闭一定数量的空调来满足系统要求。限电场景下系统可提供恢复功率决定负荷恢复量大小。为了说明系统可提供恢复功率和停电时间对负荷恢复量的影响,计算不同停电时间和系统可提供恢复功率下的关闭空调数量,如图7 所示。系统可提供恢复功率大于最大可恢复负荷量时,关闭空调数量受最大可恢复负荷量制约,保持不变;小于最大可恢复负荷量时,需要关闭的空调数量随着可提供恢复功率减少而增加。系统可提供恢复功率越小,停电时间越长,通过需求响应关闭的空调数量越多。证明在限电越严重的情况下,对可恢复负荷量的限制越多,需求响应在负荷恢复中的作用越突出。
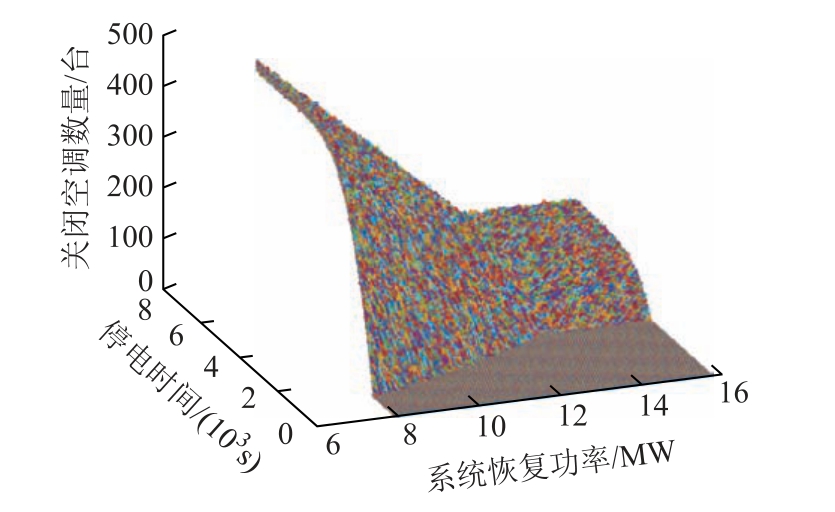
图7 关闭空调数量与系统可提供恢复功率和停电时间的关系
Fig.7 The off number of air-conditioning loads in relation to system recovery power and outage time
4.2.3 需求响应控制策略对舒适度的影响
分别采用本文的控制策略和随机控制策略实现负荷恢复量削减,比较用户舒适度受到的影响。计算两种策略下空调群H 值总和,其值越大,表明空调群整体距离温度区间越近,用户舒适度受到影响越小。以随机控制策略结果为基准,本文控制策略下空调群H 值总和与系统可提供恢复功率和停电时间的关系如图8 所示。结果表明,随着停电时间的增加和系统可提供恢复功率的减少,对比随机控制策略,本文所提策略使得空调群H 值总和变大,空调群分布距离温度区间更近,用户舒适度受到影响更小。由于本文方法优先关闭温度距离温度区间近的空调负荷,保证温度偏离严重的空调能够及时恢复供电,最大限度地减少对用户舒适度的影响。本文控制策略既实现了负荷量削减目标,又兼顾了对用户舒适度的影响。
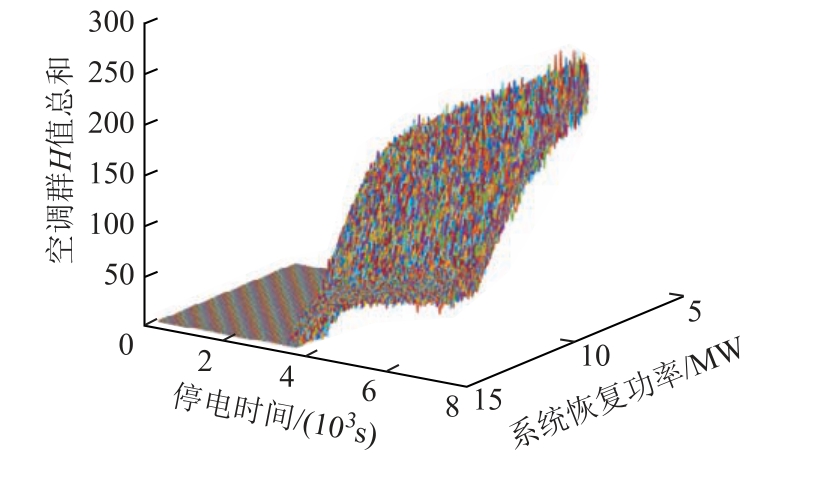
图8 两种方法空调群H 值总和差值与系统可提供恢复功率和停电时间的关系
Fig.8 The sum of the difference H values of air conditioning loads in two methods as a function of system recovery power and outage time
5 结论
本文提出了考虑空调负荷需求响应的负荷恢复量削减方法。理论分析和算例仿真结果表明,所建立的空调负荷群聚合功率估计模型能够有效地计及冷负荷启动特性,计算停电后空调负荷聚合功率;变电站恢复能力计算模型同时考虑了稳态和暂态电压约束、频率约束,快速计算变电站单次最大可恢复负荷量;提出了基于需求响应的负荷恢复量削减方法,通过削减超出上限的负荷量,满足系统限电场景以及变电站单次最大可恢复负荷量的要求,实现不同停电场景下包含大量空调负荷系统的可靠恢复。本文为电网恢复期间需求响应的应用提供了借鉴思路。
[1]许寅,和敬涵,王颖,等.韧性背景下的配网故障恢复研究综述及展望[J].电工技术学报,2019,34(16):3416-3429.
Xu Yin,He Jinghan,Wang Ying,et al.A review on distribution system restoration for resilience enhancement[J].Transactions of China Electrotechnical Society,2019,34(16):3416-3429.
[2]刘玉田,王洪涛,叶华.电力系统恢复理论与技术[M].北京:科学出版社,2014.
[3]Liu Yutian,Fan Rui,Terzija V.Power system restoration:a literature review from 2006 to 2016[J].Journal of Modern Power Systems and Clean Energy,2016,4(3):332-341.
[4]吴润基,王冬晓,谢昌鸿,等.空调负荷参与配电网电压管理的分布式控制方法[J].电力系统自动化,2021,45(6):215-222.
Wu Runji,Wang Dongxiao,Xie Changhong,et al.Distributed control method for air-conditioning load participating in voltage management of distribution network[J].Automation of Electric Power Systems,2021,45(6):215-222.
[5]何剑,屠竞哲,孙为民,等.美国加州“8·14”、“8·15”停电时间初步分析及启示[J].电网技术,2020,44(12):4471-4479.
He Jian,Tu Jingzhe,Sun Weimin,et al.Preliminary analysis and lessons of California power outage events on August 14 and 15,2020[J].Power System Technology,2020,44(12):4471-4479.
[6]胡秦然,丁昊晖,陈心宜,等.美国加州2020 年轮流停电事故分析及其对中国电网的启示[J].电力系统自动化,2020,44(24):11-18.
Hu Qinran,Ding Haohui,Chen Xinyi,et al.Analysis on rotating power outage in California in 2020 and its enlightenment to power grid in China[J].Automation of Electric Power Systems,2020,44(24):11-18.
[7]Gholami A,Aminifar F.A hierarchical response-based approach to the load restoration problem[J].IEEE Transactions on Smart Grid,2017,8(4):1700-1709.
[8]覃智君,侯云鹤,李大虎,等.输电网负荷恢复方案的优化计算方法[J].电工技术学报,2016,31(8):116-124.
Qin Zhijun,Hou Yunhe,Li Dahu,et al.Optimization method for constructing load restoration strategy of transmission systems[J].Transactions of China Electrotechnical Society,2016,31(8):116-124.
[9]程改红,徐政.基于粒子群优化的最优负荷恢复算法[J].电力系统自动化,2007,31(16):62-65.
Chen Gaihong,Xu Zheng.Optimal load restoration based on particle swarm optimization[J].Automation of Electric Power Systems,2007,31(16):62-65.
[10]Medina D R,Rappold E,Sanchez O,et al.Fast assessment of frequency response of cold load pickup in power system restoration[J].IEEE Transactions on Power System,2016,31(4):3249-3256.
[11]Schneider K P,Sortomme E,Venkata S S,et al.Evaluating the magnitude and duration of cold load pick-up on residential distribution feeders using multistate load models[J].IEEE Transactions on Power System,2016,31(5):3765-3774.
[12]Gilvanejad M,Abyaneh H A,Mazlumi K.Estimation of cold-load pickup occurrence rate in distribution systems[J].IEEE Transactions on Power Delivery,2013,28(2):1138-1147.
[13]王成山,刘梦璇,陆宁.采用居民温控负荷控制的微网联络线功率波动平滑方法[J].中国电机工程学报,2012,32(25):36-43.
Wang Chengshan,Liu Mengxuan,Lu Ning.A tie-line power smoothing method for microgrid using residential thermostatically-controlled loads[J].Proceedings of the CSEE,2012,32(25):36-43.
[14]王蓓蓓,胡晓青,顾伟扬,等.分层控制架构下大规模空调负荷参与调峰的分散式协同控制策略[J].中国电机工程学报,2019,39(12):3514-3527.
Wang Beibei,Hu Xiaoqing,Gu Weiyang,et al.Hierarchical control architecture and decentralized cooperative control strategy for large scale air conditioning load participating in peak load regulation[J].Proceedings of the CSEE,2019,39(12):3514-3527.
[15]肖天颖,裴玮.陈乃仕,等.考虑空调负荷削负荷能力不确定性的孤岛最大运行时长评估[J].中国电机工程学报,2019,39(17):4982-4994.
Xiao Tianying,Pei Wei,Chen Naishi,et al.Maximum operation duration assessment of isolated island considering the uncertainty of load reduction capability of air conditioner[J].Proceedings of the CSEE,2019,39(17):4982-4994.
[16]贾雨龙,米增强,余洋,等.计及不确定性的柔性负荷聚合商随机-鲁棒投标决策模型[J].电工技术学报,2019,34(19):4096-4107.
Jia Yulong,Mi Zengqiang,Yu Yang,et al.Stochasticrobust decision-making model for flexible load aggregator considering uncertainties[J].Transactions of China Electrotechnical Society,2019,34(19):4096-4107.
[17]李亚平,姚建国,雍太有,等.居民温控负荷聚合功率及响应潜力评估方法研究[J].中国电机工程学报,2017,37(19):5519-5528.
Li Yaping,Yao Jianguo,Yong Taiyou,et al. Estimation approach to aggregated power and response potential of residential thermostatically controlled loads[J].Proceedings of the CSEE,2017,37(19):5519-5528.
[18]吴界辰,艾欣,胡俊杰.需求侧资源灵活性刻画及其在日前优化调度中的应用[J].电工技术学报,2020,35(9):1973-1984.
Wu Jiechen,Ai Xin,Hu Junjie.Methods for characterizing flexibilities from demand-side resources and their applications in the day-ahead optimal scheduling[J].Transactions of China Electrotechnical Society,2020,35(9):1973-1984.
[19]Qu Hanbing,Liu Yutian.Maximizing restorable load amount for specific substation during system restoration[J].International Journal of Electrical Power &Energy Systems,2012,43(1):1213-1220.
[20]Adibi M M,Borkoski J N,Kafka R J,et al. Frequency response of prime movers during restoration[J].IEEE Transactions on Power System,1999,14(2):751-756.
[21]常烨骙,李卫东,巴宇,等.基于运行安全的频率控制性能评价新方法[J].电工技术学报,2019,34(6):1218-1229.
Chang Yekui,Li Weidong,Ba Yu.A new method for frequency control performance assessment on operation security[J]. Transactions of China Electrotechnical Society,2019,34(6):1218-1229.
[22]宁佳,汤奕,高丙团.基于需求响应潜力时变性的风火荷协同控制方法[J].电工技术学报,2019,34(8):1728-1738.
Ning Jia,Tang Yi,Gao Bingtuan.Coordinated control method of wind farm-AGC unit-load based on timevarying characteristics of demand response potential[J].Transactions of China Electrotechnical Society,2019,34(8):1728-1738.
[23]Cheng Dingyi,Zhang Wei,Liu Yutian.Aggregate modeling and analysis of air conditioning load using coupled Fokker–Planck equations[J].Journal of Modern Power Systems and Clean Energy,2018,6(6):1277-1290.