0 引言
近年来,光伏、储能等直流型分布电源,以及电动汽车、数据中心等直流型负载在配电网中的比例逐渐增加,配电网的“直流特性”越发明显[1-5]。然而,直流型分布式电源或负载接入交流配电网不仅增加了转换环节,而且还可能导致配电网的频率稳定、无功补偿等问题[5]。通过直流配电网连接分布式电源或直流负载,既可减少转换环节,还可增强配电网的电能质量、供电可靠性和供电容量[1-5]。然而,在环状结构的直流电网中,换流站之间可能存在多条线路,使得输电线路的数量大于等于换流站数量,导致线路上的潮流不能仅依靠换流站的电压、功率控制实现有效调节。在这种情况下,直流电网部分线路潮流可能因得不到有效控制而导致线路过载,威胁系统的安全有效运行[6-9]。
为增加直流配电网潮流控制的自由度,许多学者将潮流控制器(Power Flow Controller,PFC)引入直流配电网[10]。根据其与配电网的连接方式,PFC 可分为串联型、并联型和串并联型[11]。其中串联型PFC主要包括可变电阻型PFC 和线间PFC。文献[12-14]提出了三种基于可变电阻器的直流潮流控制方案,其基本原理是通过改变串入线路的等效电阻调节线路潮流。电阻型潮流控制器结构简单、易于控制,但其运行损耗较高且只能单向调节线路潮流。
线间PFC 通过不同直流线路之间的能量交换实现潮流控制[15-18]。在正常工作模式下,线间PFC 通过将一个电容分时串入两条独立的直流线路实现调节潮流,其具有结构简单、成本低等优点,但是会引入电流纹波[11]。并联型PFC 本质上是一个直流变压器,其通过控制直流变压器输出直流电压调节线路潮流。然而,并联型PFC 需承担系统级的电压和电流,成本较高且运行损耗较大[12,19]。文献[20-22]提出了串并联PFC(Series-Parallel PFC,SP-PFC)的拓扑,其输入与直流母线并联,输出与直流线路串联。该PFC 的高低压侧通过高频隔离变压器连接,因此该PFC 只需承受系统的部分功率,成本较低且控制能力较强。
与单极直流配电网相比,双极直流配电网具有多电压接口,接地可靠,且能满足用户的多样化需求[6,23]。然而,由于存在中线电阻,当正、负极之间存在功率不平衡时,正、负极间耦合特性明显[23]。文献[24]分析了双极直流配电网的耦合电压特性,并提出利用直流电力弹簧(DC Electric Spring,DC-ES)抑制不平衡电压。然而,电力弹簧仅能调节不平衡负荷,无法实现系统级的潮流控制。为了实现对单极直流配电网的潮流控制,文献[7]研究了SPPFC 在单极直流配电网中的潮流控制特性,分析了SP-PFC 的工作原理及其控制策略。但若SP-PFC 应用在环形双极直流配电网中,需额外增加SP-PFC 的数量;文献[22]提出了三有源桥串并联直流潮流控制器(Triple Active Bridge Power Flow Controller,TAB-PFC)拓扑,并研究了TAB-PFC 在环形双极直流配电网中的应用,分析了TAB-PFC 的控制模式,但没有验证其潮流控制性能,也未结合环形双极直流配电网的网络特性(如正负极电压的耦合特性、负荷的不平衡、受端电压的不平衡和新能源出力的不平衡)提出TAB-PFC 的控制方法。
为实现环形双极直流配电网不平衡潮流的抑制,本文提出一种基于TAB-PFC 的不平衡潮流抑制策略。相比基于双有源桥的SP-PFC,所采用的拓扑可以减少隔离变压器和高压侧电力电子器件的数量。
此外,为了增强TAB-PFC 在环形双极直流配电网潮流控制的动态性能,本文分析了受端电压、新能源出力不平衡时环形双极直流配电网的正、负极耦合特性,推导了正、负极潮流和线路损耗与不平衡受端电压的关系。在此基础上,推导了恒功率控制下TAB-PFC 输出电压和线路电流的表达式,建立了含TAB-PFC 的环形双极直流配电网的稳态模型和小信号模型。在模型的基础上,引入参数解耦矩阵实现正负极控制环路间的近似解耦。在Matlab/Simulink 中建立了含TAB-PFC 的环形双极直流配电网的仿真模型,并搭建了实验平台。仿真和实验结果验证了TAB-PFC 抑制不平衡潮流及参数解耦矩阵方法的有效性。
1 环形双极直流配电网不平衡潮流分析
1.1 TAB-PFC 的拓扑
TAB-PFC 的拓扑如图1 所示。S1~S12 和Q1~Q8是TAB-PFC 的开关管;Cin 为PFC 的输入电容;Vdci和Cdci 分别为TAB 的输出电压和输出电容;Lfi 和Cfi 为滤波电感和滤波电容,其中i=1,2;vk1 和vk2 为TAB-PFC 的输出电压;T 为三绕组隔离变压器,Lσ1、Lσ2、Lσ3 分别为三绕组隔离变压器一、二次侧的漏感;Vs、V1、V2 分别为送端和受端电压;RL1 和RL2分别为正、负极线路的线路电阻。

图1 TAB-PFC 拓扑
Fig.1 The topology of TAB-PFC
此拓扑由三有源桥(Triple Active Bridge,TAB)和全桥变换器(Full-Bridge Converter,FBC)构成。TAB 的一次侧与直流母线并联,一、二次侧通过隔离变压器T 连接,FBC 的输出电压串联连接至直流输电线路中。
1.2 含TAB-PFC 的不平衡潮流分析
TAB-PFC 应用于环形双极直流配电网的示意图如图2a 所示,图中L1~L3 表示直流传输线路,Ip、Inu、In 分别为正极、中线、负极传输线的电流。TAB-PFC 安装在N1 节点的出口处。N1~N3 节点的等效电路如图2b 所示,其中N1、N2 节点表示电压可控的换流站,N3 节点表示功率可控的换流站。

图2 含TAB-PFC 的环形双极直流配电网等效电路
Fig.2 Equivalent circuit of ring bipolar DC distribution network with TAB-PFC
假设N2 节点的正、负电压不平衡或N3 节点出力不平衡。为分析及控制线路潮流,推导了含TABPFC 的线电流、线路潮流、线路损耗的表达式。
根据图 2b,对其列写节点电压方程及补充方程为
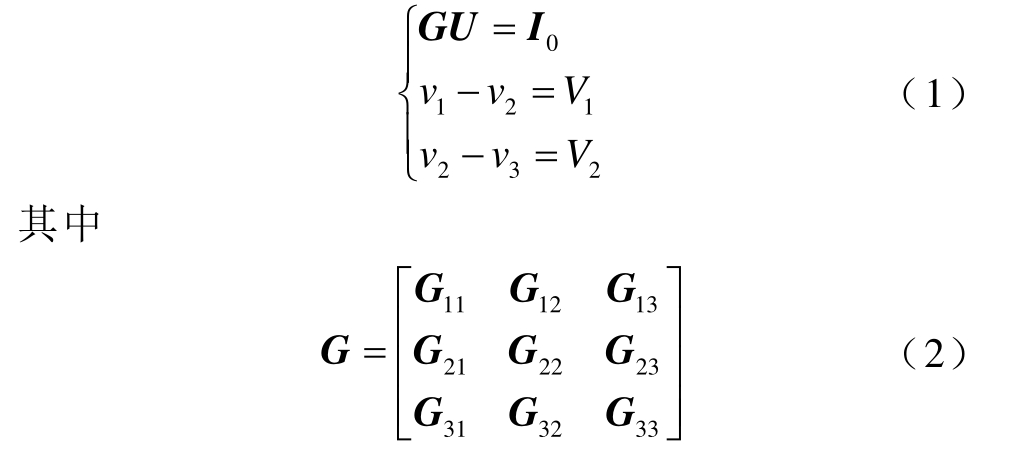
式中各参数表达式详见附录。

各线路上电流I 为
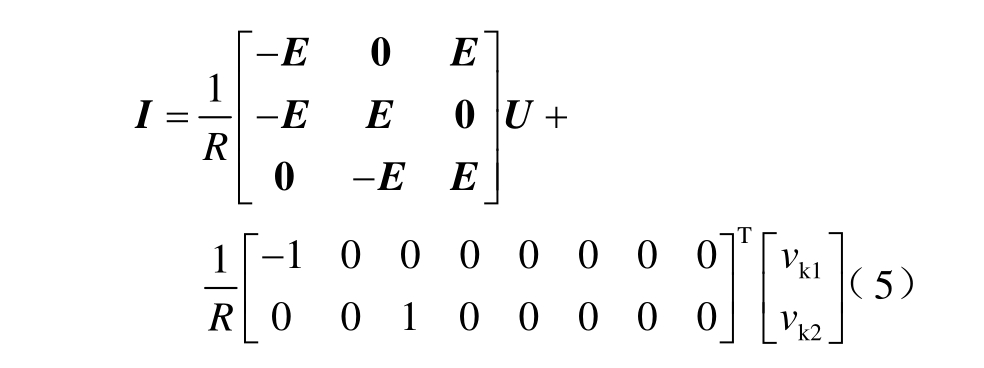
式中,E 与0 分别为三维单位矩阵与三维零矩阵。
线路损耗为
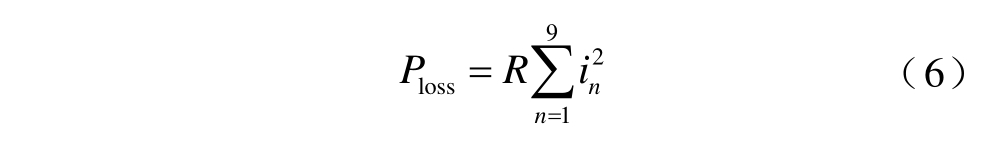
正、负极线路传输的功率P1、P2 为

当添加TAB-PFC 时,将式(7)作为约束条件,P1、P2 作为给定值控制PFC 的输出电压vk1 和vk2。
1.3 不平衡功率对TAB-PFC 的影响
1.3.1 受端电压不平衡对TAB-PFC 影响
为研究不平衡的受端电压对线路潮流的影响以及TAB-PFC 的作用,图2b 的各电路元件参数设置如下:Vs=400V,Rs=0.01Ω,R=0.1Ω,P01=P02=10kW,V01=V02=400V,V2=400V,V1 从380V 变化至420V, P1 和P2 的期望值均设置为10kW。
受端电压不平衡时有、无TAB-PFC 线路潮流对比如图3 所示。当无TAB-PFC 时,线路潮流随受端电压的变化而变化,无法达到期望值;加入TABPFC 后,线路的潮流恒定为期望值。
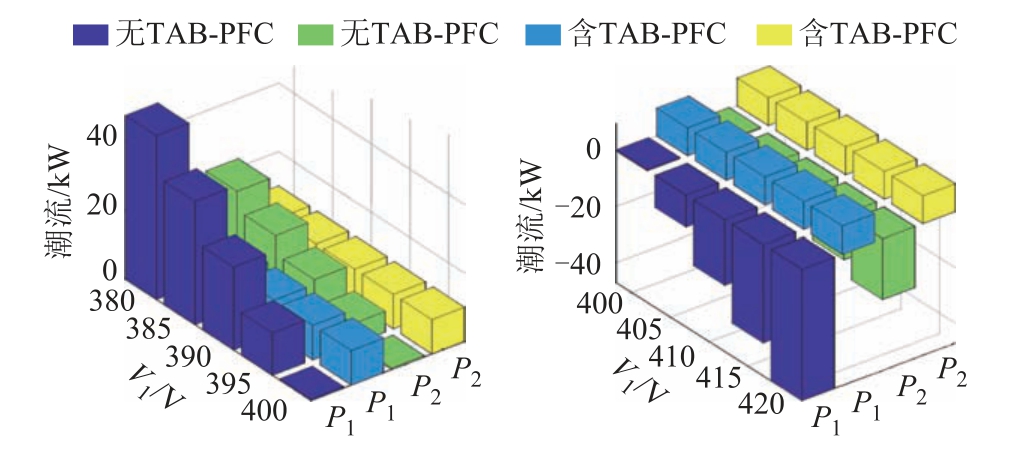
图3 受端电压不平衡时有无TAB-PFC 线路潮流对比
Fig.3 Comparison of power flow with/without TAB-PFC under unbalanced receiving-end voltage
受端电压不平衡时TAB-PFC 输出电压及有、无TAB-PFC 线路损耗如图4 所示。由图4a 可知,TABPFC 的输出电压vk1 和vk2 随受端电压V1 的变化而灵活调节。由图4b 可知,TAB-PFC 的加入显著降低了受端电压不平衡时的线路损耗。

图4 受端电压不平衡时TAB-PFC 输出电压及有无TAB-PFC 线路损耗
Fig.4 TAB-PFC output and line loss with/without TABPFC under unbalanced receiving-end voltage
1.3.2 新能源出力不平衡对TAB-PFC 的影响
考虑到新能源出力常为光伏,其出力具有很强的不确定性,受天气、时间变化影响较大,典型的光伏小时功率曲线近似为二次曲线[25]。24h 光伏出力及线路潮流如图5 所示。PV 为光伏出力,Pp 为正极线路潮流,Pn 为负极线路潮流。图 5 中V1=V2=400V,当无TAB-PFC 时,线路潮流随时间增长和光伏出力变化而变化,无法达到期望的功率。而通过控制TAB-PFC 灵活输出vk1 和vk2 可控制线路潮流恒定,如图6 所示。
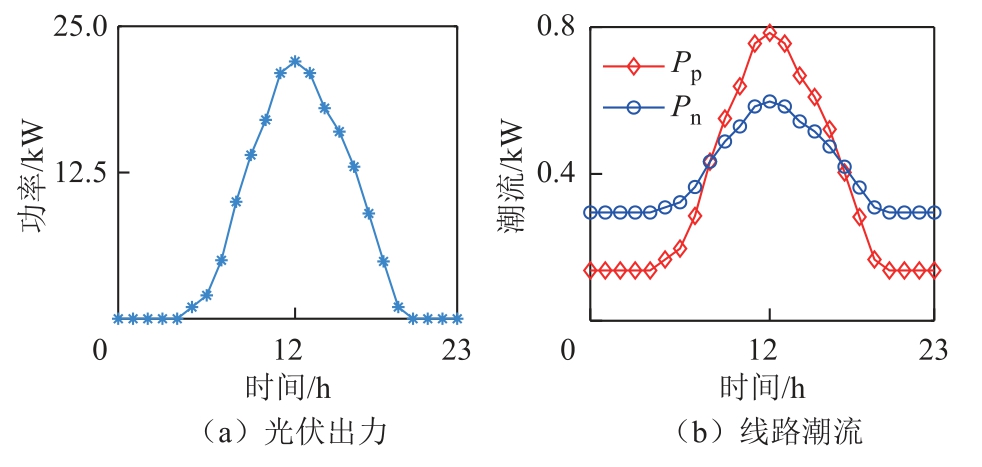
图5 24h 光伏出力及线路潮流
Fig.5 24h photovoltaic output power and line power
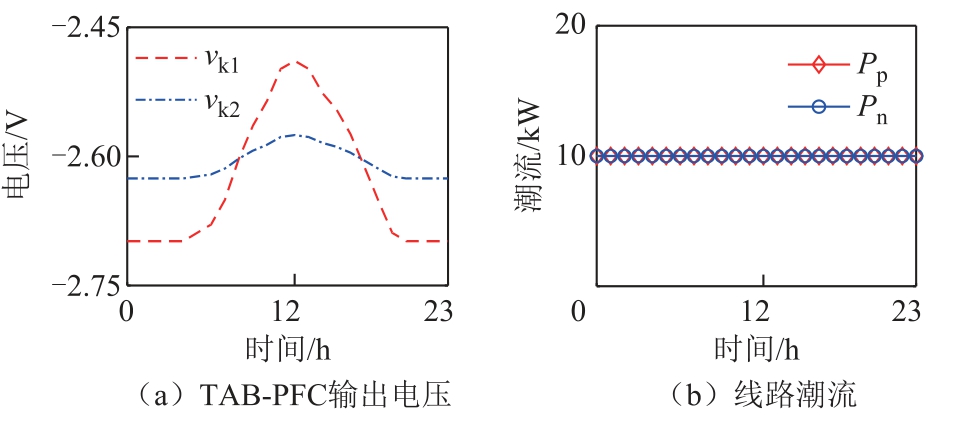
图6 TAB-PFC 输出电压及线路潮流
Fig.6 TAB-PFC output voltage and line power
2 小信号分析
2.1 含TAB-PFC 的环形双极直流配电网的小信号建模与分析
将式(7)代入式(1)和式(5)可得正、负极线路电流Ip、In,正、负极线路电压vLp、vLn 与vk1和vk2 间的关系为
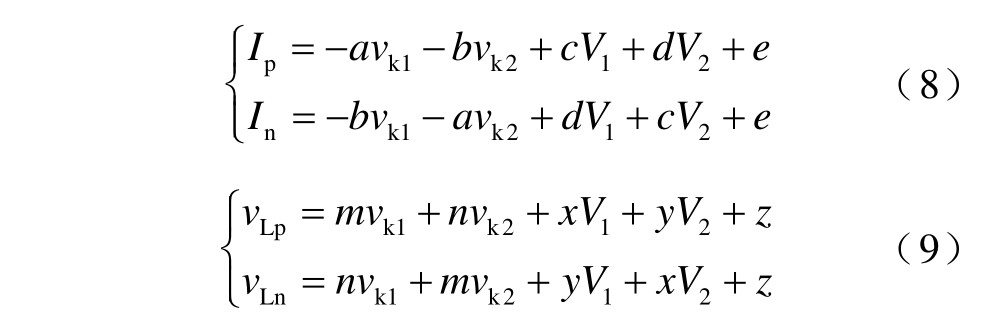
式中,a、b、c、d、e,m、n、x、y、z 的表达式详见式(A2)与式(A3)。
为便于描述,假设TAB 的输出Vdc1=Vdc2,对于FBC,TAB 输出Vdc 可视为恒定值,简化后的TAB-PFC 如图7 所示。

图7 简化的含TAB-PFC 环形双极直流配电网
Fig.7 Simplified ring bipolar DC distribution network with TAB-PFC
将电感电流和TAB-PFC 的输出电压作为状态变量可得到其状态方程为
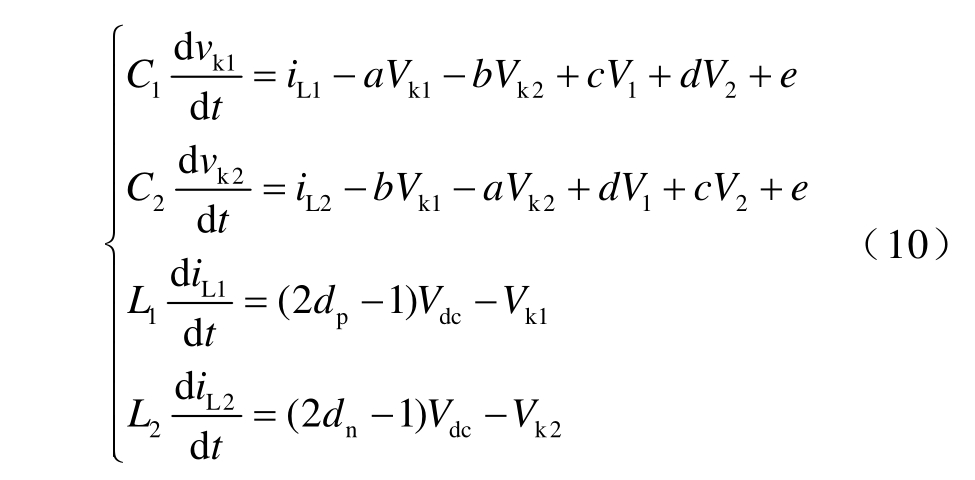
式中,C1、C2,L1、L2 分别为TAB-PFC 正负极的滤波电容和滤波电感;dp 和dn 分别为正、负极FBC 开关管的占空比;vk1 和vk2 分别为Vk1 和Vk2 的暂态值。由式(10)可得含TAB-PFC 的环形双极直流配电网的小信号模型为

根据式(11)可推导控制至输出的传递函数,正极FBC 占空比dp 至输出vk1 和vk2 的传递函数Gpp(s)和Gpn(s)为
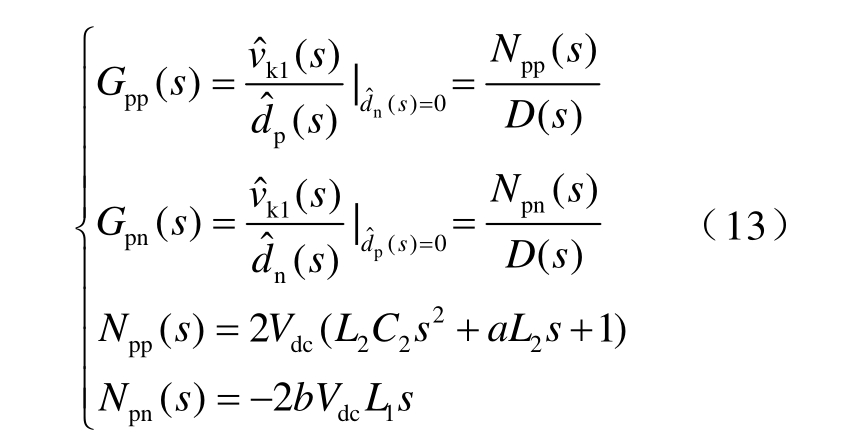
其分母表达式为
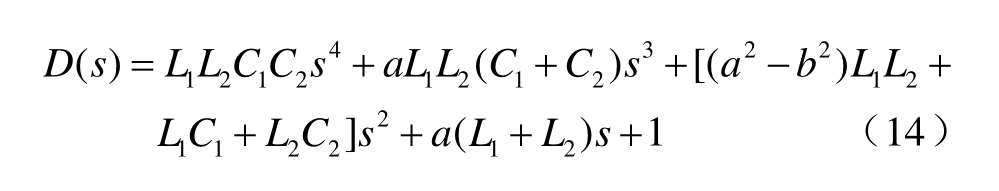
式中,上标“ˆ”为变量的交流小信号分量。
dp 和dn 与vk1 和vk2 的关系矩阵如式(15)所示,该系统为双输入双输出系统,当TAB-PFC 正负极FBC 参数一致时,有Gpp(s)=Gnn(s),Gpn(s)= Gnp(s)。
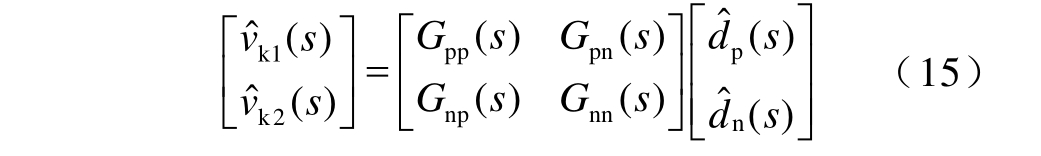
由于Gpn 与Gnp 的存在,FBC 正、负极的控制回路之间存在耦合关系,解耦网络W 可以对其进行解耦。解耦网络将多变量系统分解为两个独立的单回路子系统,各子系统的控制器可以独立设计。该方法的控制系统框图如图8 所示,G 表示双极直流配电网中TAB-PFC 输出电压的小信号传递函数,W表示解耦网络的传递函数。![]() 分别为所期望的TAB-PFC 正、负极输出电压值,Gcvp(s)与Gcvn(s)分别为正、负极电压环的补偿器传递函数。
分别为所期望的TAB-PFC 正、负极输出电压值,Gcvp(s)与Gcvn(s)分别为正、负极电压环的补偿器传递函数。
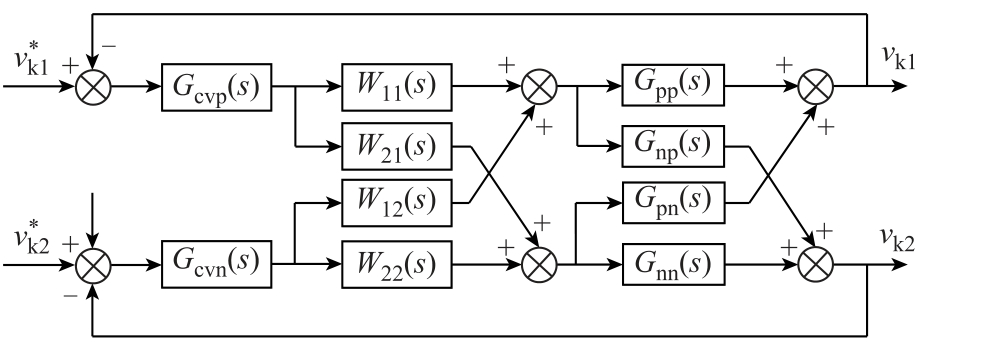
图8 FBC 理想解耦网络方法控制系统框图
Fig.8 FBC ideal decoupling network control system block diagram
若使X=GW=diag(1,1),则控制系统的主对角线元素均为1,副对角线元素均为0,此时TAB-PFC正、负极输出电压跟随各自的给定值,互不影响。解耦矩阵为
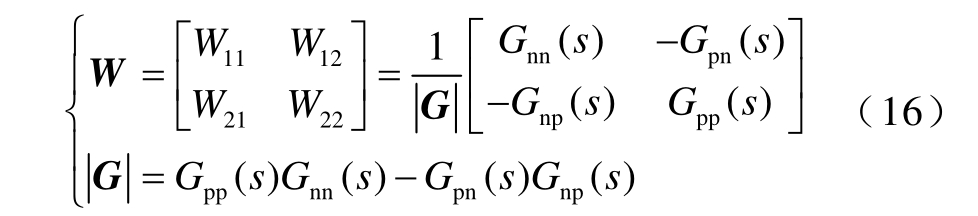
2.2 解耦控制的实现
式(16)中所示解耦矩阵是理想情况下的形式,但由于W 矩阵中各项为传递函数形式,且包含的二阶微分项很容易受到高频噪声的影响,其实现较为复杂,因此本研究引入解耦控制变量k1 和k2 进行解耦。k1 和k2 由坐标变换引入,并且使用k1、k2、dp、dn 的Jacobian 矩阵来替代理想的W。TAB-PFC 输出电压大信号模型表达式为
故式(9)可写为
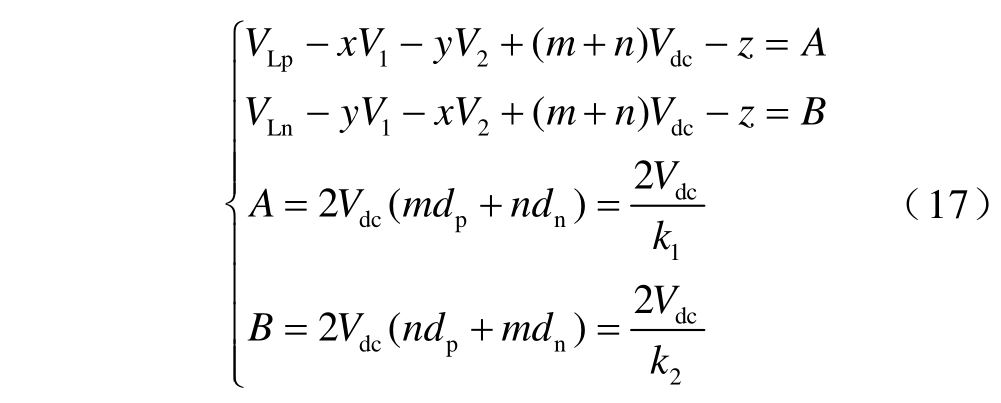
式中,k1 和k2 为解耦控制变量。式(17)表明,vLp 与k2 无关,vLn 与k1 无关。根据式(17),k1 和k2 满足
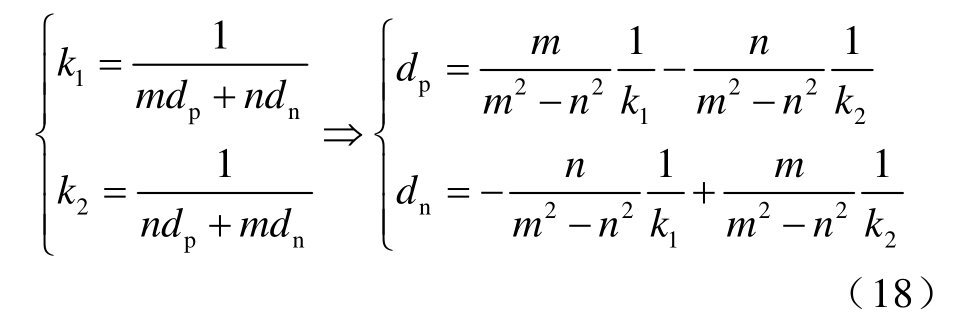
dp、dn、k1、k2 的Jacobian 矩阵可由式(19)得到。

式中,K1、K2 分别为k1、k2 的稳态值。根据式(17),K1、K2 满足
与式(16)相比,式(19)解耦矩阵中所有元素均为常数,更容易实现。引入解耦网络后的传递函数为
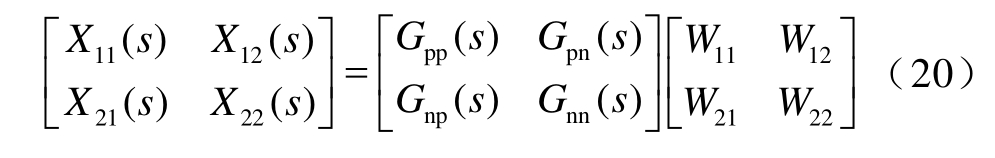
式中,X11(s)、X12(s)、X21(s)和X22(s)为引入参数解耦网络后的传递函数。
若实现了式(16)所示的理想解耦矩阵W,G(s)和X(s)的Bode 图如图9 所示。图9b 表明在引入解耦控制矩阵后,副对角线的增益被大幅衰减,有效地消除了来自其他极的干扰,但其实现较为复杂。
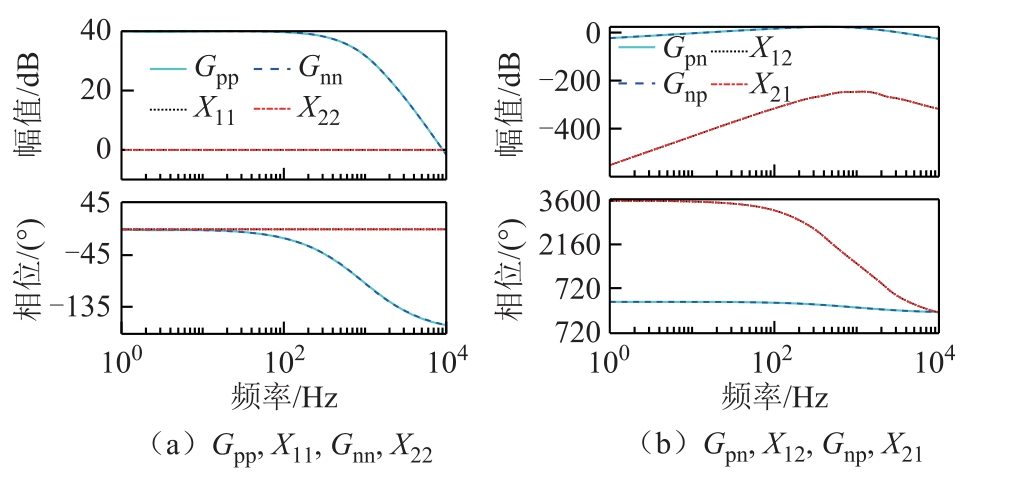
图9 理想解耦矩阵W 下的Bode 图
Fig.9 Bode diagram under ideal decoupling matrix W
若采用式(19)所示的参数解耦矩阵W,G(s)和X(s)的Bode 图如图10 所示,其中W 采用额定参数设计。根据式(19)计算得到 W11=0.178 2,W12=0.006 8,W21=0.005 2,W22=0.230 0。由图10b,与Gpn 和Gnp 相比,X12 和X21 在最高点的衰减量超过15dB,低频幅值在0 以下,实现了近似解耦。式(19)中所示的W 简单且易于实现,因此本研究采用式(19)所示的参数解耦网络。
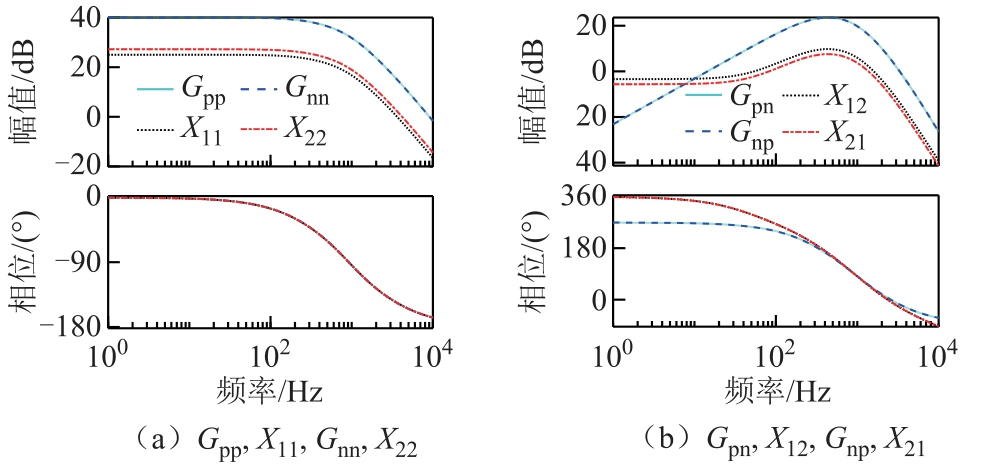
图10 参数解耦矩阵W 下的Bode 图
Fig.10 Bode diagram under parameter decoupling matrix W
2.3 控制器设计
设计FBC 中电压补偿器参数时,电压环的开关频带应比开关频率低,综合考虑稳态性能与动态性能,截止频率一般设计为开关频率的1/10~1/20[26]。基于此,选择截止频率为2.5kHz 的双极点双零点补偿器[27],其传递函数为
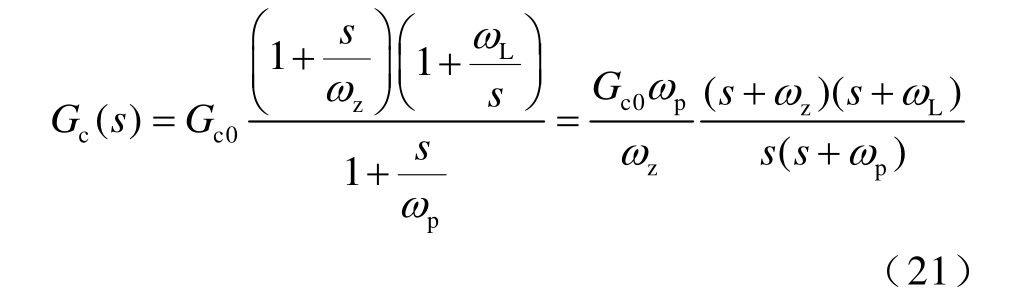
其中,Gc0=0.129,零点频率fz=1.72kHz,极点频率fp=14.52kHz,转折频率fL=400Hz,ω=2πf。
选择FBC 中功率补偿器参数时,功率环的带宽应为电压内环带宽的1/10。基于此,选择功率外环补偿器为PI 控制器,其Kp=0.01,Ki=2。
3 仿真结果分析
3.1 不含TAB-PFC 的仿真结果
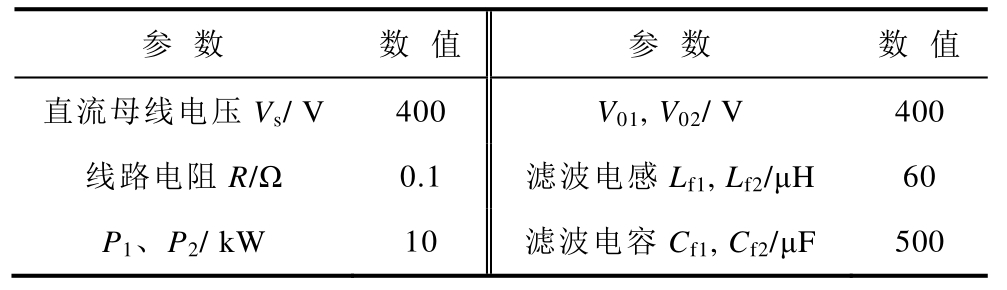
为验证所提方法的正确性与有效性,在Matlab/Simulink 环境下建立如图11 所示的环形双极直流配电网的模型。其中V1=390V,V2=400V,Rs=0.01Ω,模型中其他参数见表1,系统参数包括电压等级、线路电阻、线路传输功率参考自文献[22,28];TAB-PFC 的参数主要包括滤波电感和滤波电容,滤波电感按纹波电流要求进行设计,滤波电容结合滤波器的剪切频率进行设计[27]。不含TAB-PFC 时正、负极线路潮流分别为24.13kW 与11.47kW,无法达到期望的恒定值10kW。

图11 环形双极直流配电网仿真示意图
Fig.11 Schematic diagram of ring bipolar DC distribution network simulation
表1 环形双极直流配电网参数
Tab.1 The parameters of ring bipolar DC distribution network
3.2 含TAB-PFC 的仿真结果
TAB 的解耦控制详见文献[29],TAB 采用恒电压控制以使输出电压Vdc 恒定。FBC 采用恒功率控制以使线路潮流恒定,其控制策略如图12 所示,其 中iL、vL、Pt 分别为传输线路的电流、电压和潮流。![]() 分别为Pt 和vL 的给定值,Gcp(s)和Gcv(s)分别为功率外环和电压内环补偿器。
分别为Pt 和vL 的给定值,Gcp(s)和Gcv(s)分别为功率外环和电压内环补偿器。

图12 TAB-PFC 解耦控制框图
Fig.12 TAB-PFC decoupling control block diagram
3.2.1 受端电压不平衡
图13 所示为受端电压不平衡时的仿真结果。其中P、I 为线路潮流和线路电流,下标p、n 代表正负极。在0.06s 时,V1 从390V 变化至420V,由图13a,Pp 与Pn 不受V1 变化影响,稳定维持在期望值10kW。由图13b,受端电压突变前后线路电流变化较小。对比解耦前后的线路潮流和线路电流,可以观察到在未进行网络解耦前,线路潮流以及线路电流的纹波较大,线路潮流纹波为700W,在经过解耦后,纹波减小,增强了系统的动态性能。

图13 受端电压不平衡仿真结果
Fig.13 Simulations under unbalanced voltage of the receiving end
图14 所示为有无TAB-PFC 时环形双极直流微网线路损耗对比,在0.06s 时,某一极电压发生跳变。由图14 可知TAB-PFC 在控制潮流恒定的同时还能减小线路损耗,与1.3.1 节分析一致。
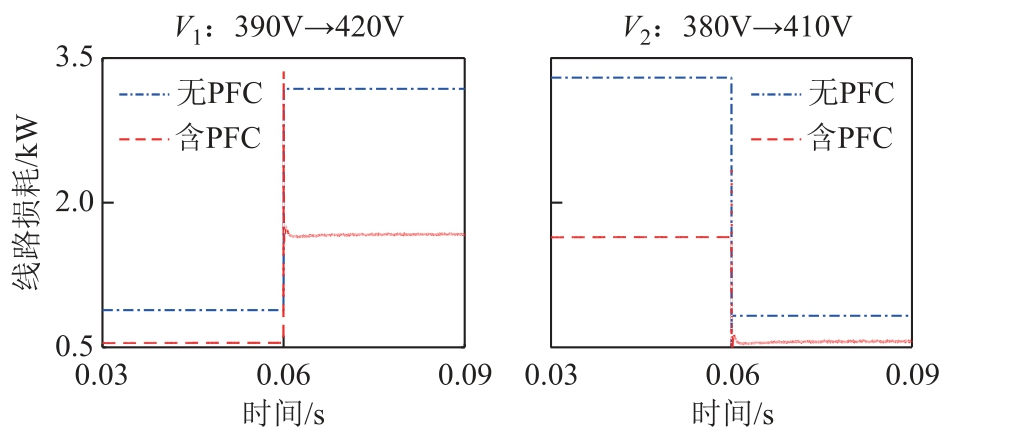
图14 有、无TAB-PFC 线路损耗对比
Fig.14 Line loss contrast with/without TAB-PFC
3.2.2 新能源出力不平衡
图15 为受端电压平衡(V1=V2=400V),正负极新能源出力不平衡时的仿真结果,各符号代表含义与受端电压不平衡时仿真结果一致。0~0.09s 为稳态建立过程,正、负极新能源出力和受端电压处于额定平衡状态。0.10~0.33s 正极新能源出力模拟24h 内光伏输出,光伏出力变化曲线与1.3.2 节一致,负极光伏出力保持额定值不变。图15a、图15b 所示分别为线路潮流与线路电流波形,可见在TAB-PFC 恒功率控制下,二者均保持恒定。图15c 所示为TABPFC 输出的电压,其随光伏出力的变化而灵活调节。由于负极光伏出力保持恒定,该极TAB-PFC 功率及输出电压变化幅度较正极小。在解耦控制策略下,各波形的纹波均减小,系统的动态性能提高。

图15 光伏出力不平衡仿真结果
Fig.15 Simulations under unbalanced photovoltaic output
4 实验结果分析
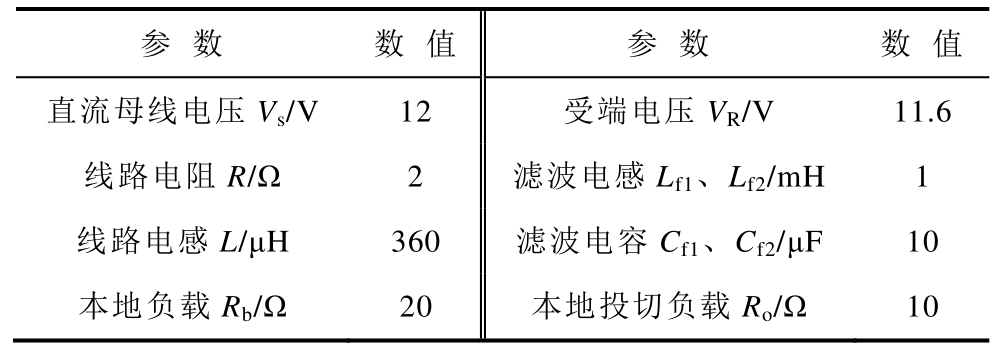
为验证本文所提不平衡潮流抑制策略的有效性,搭建了如图16 所示的含TAB-PFC 的双极直流配电网的实验平台,实验平台参数见表2,TAB-PFC采用STM32H750 控制。环形双极直流配电网中,本地负载主要可分为恒阻抗负载(Constant Resistive Load,CRL)和恒功率负载(Constant Power Load,CPL),闭环控制的变换器输出功率恒定,故可视为恒功率负载[30]。本实验中,以输出电阻为20Ω、输出电压控制为恒定10V 的Buck 变换器作为恒功率本地负载进行实验验证。

图16 实验平台
Fig.16 Experimental platform
表2 实验平台参数
Tab2 The parameter of experimental platform
4.1 有无TAB-PFC 的实验结果
在正极投切10Ω 的恒阻抗本地负载的实验结果如图17 所示。对比左右图可知,添加TAB-PFC 之后正负极电压、电流均在较短时间内重归恒定值,从而线路潮流也保持为恒定值15W。图17c 右图中潮流范围波动较大的原因是实验电源容量较小。
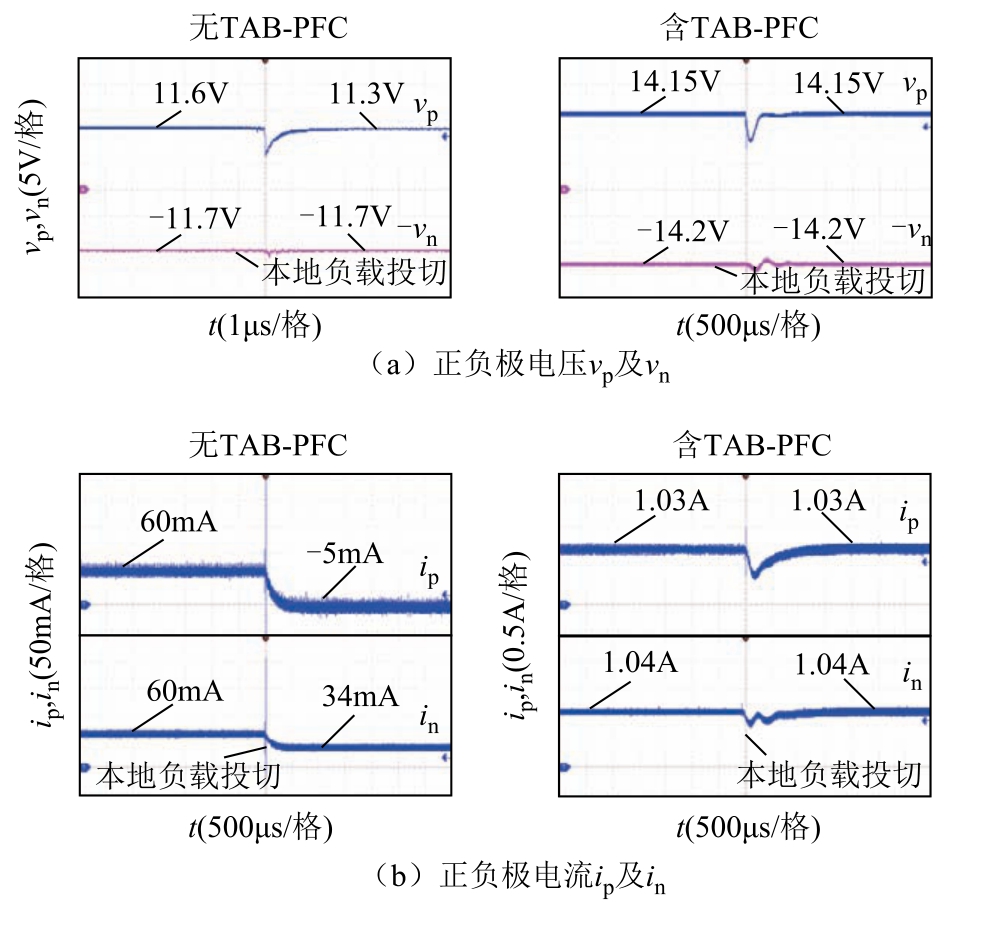
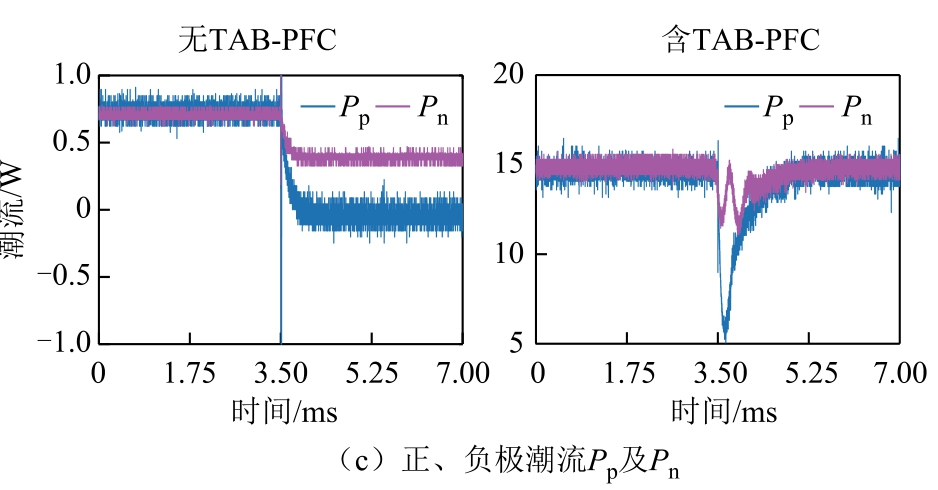
图17 恒阻抗本地负载有无TAB-PFC 的实验结果
Fig.17 Experimental results of local CRL with/without TAB-PFC
在正极投切输出电阻为10Ω 的恒功率本地负载的实验结果如图18 所示,此时正、负极受端电压分别为10.48V 和10.90V。可见添加TAB-PFC 之后不平衡潮流被抑制,线路潮流亦重归为给定值15W。
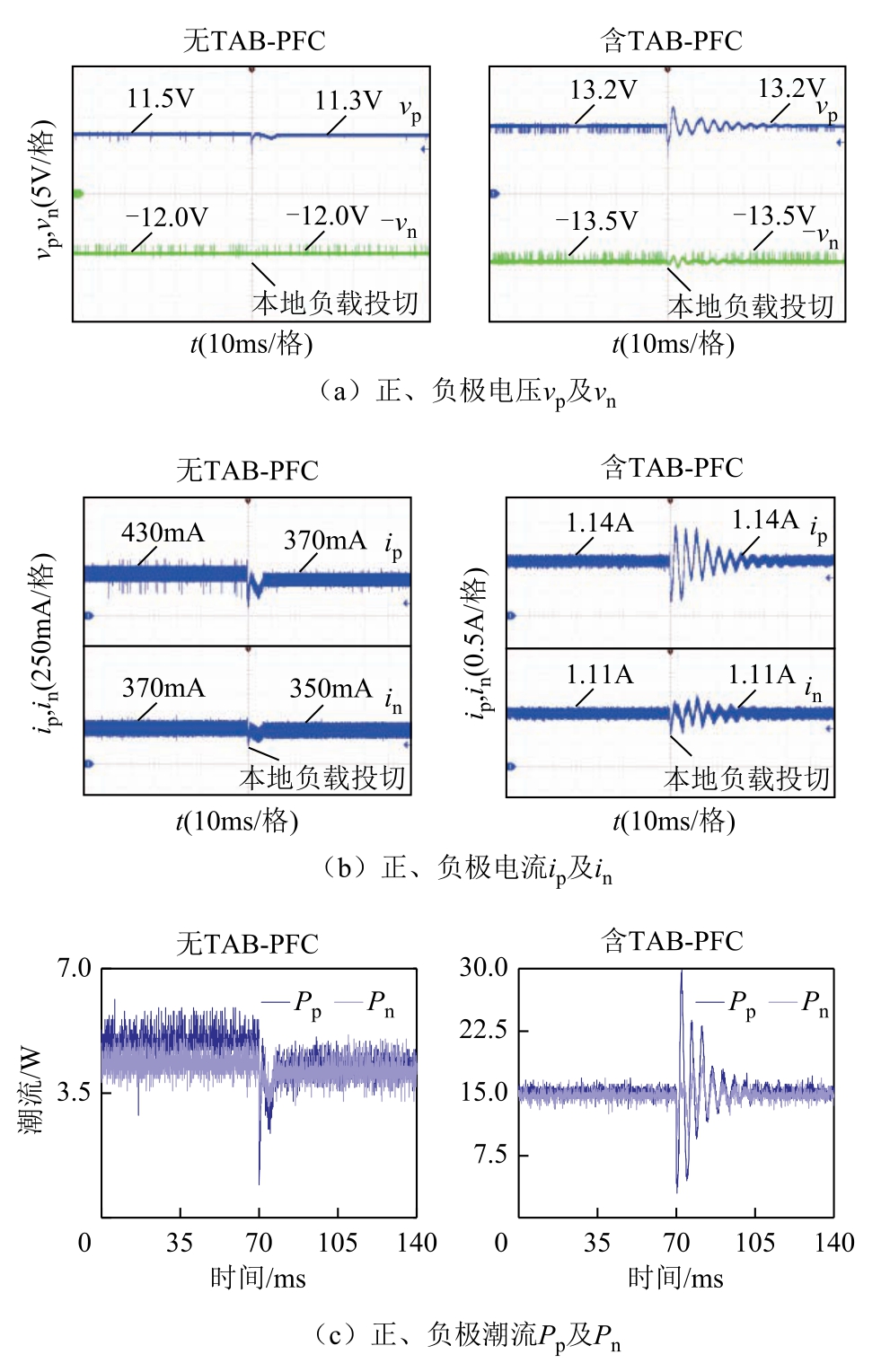
图18 恒功率本地负载有、无TAB-PFC 的实验结果
Fig.18 Experimental results of local CPL with/without TAB-PFC
4.2 有无解耦控制的实验结果
正极投切本地负载时的含TAB-PFC 的实验结果分别如图19 和图20 所示。图19 所示为投切恒阻抗负载,图20 所示为投切恒功率负载。投切恒阻抗负载时正、负极受端电压分别为10.6V、11.6V;投切恒功率负载时正、负极受端电压分别为11.12V、11.96V。对比左右图,在TAB-PFC 抑制不平衡功率的基础上,所提解耦控制策略减小了各波形纹波,实现近似解耦。

图19 恒阻抗本地负载有无解耦控制的实验结果
Fig.19 Experimental results of local CRL with/without decoupling control strategy
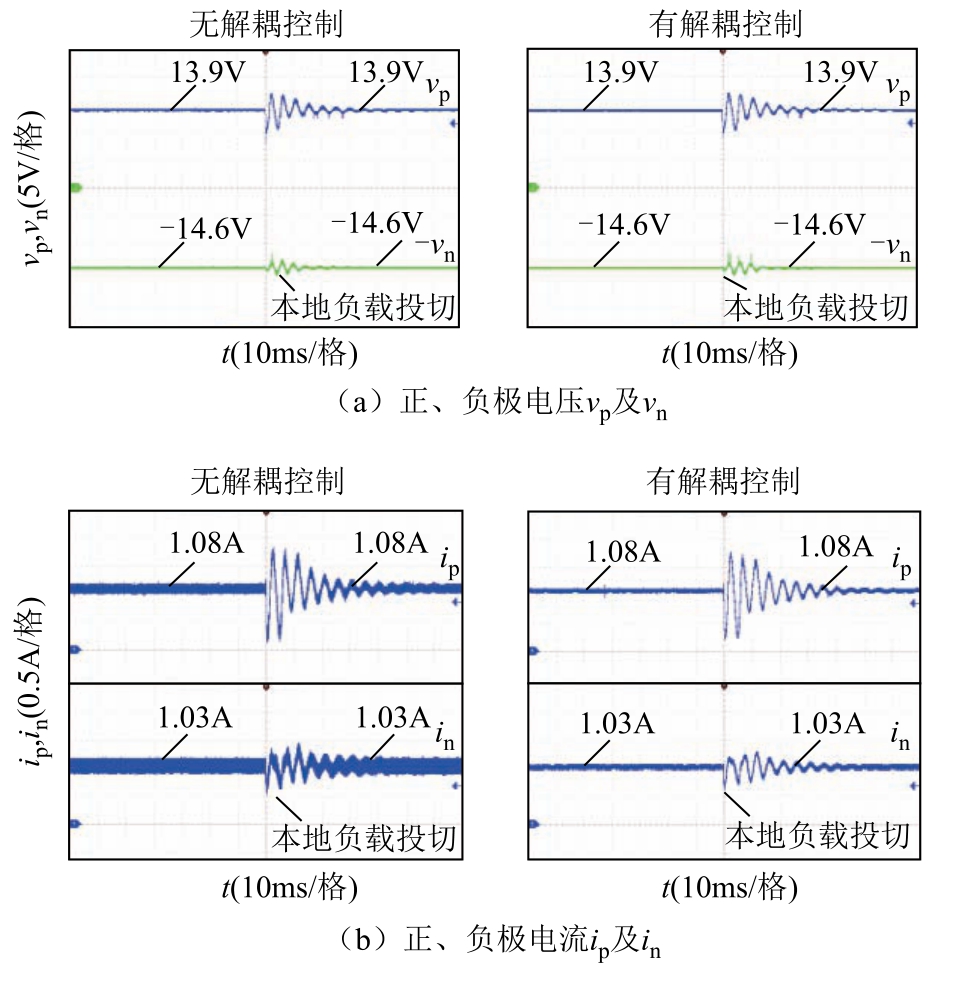
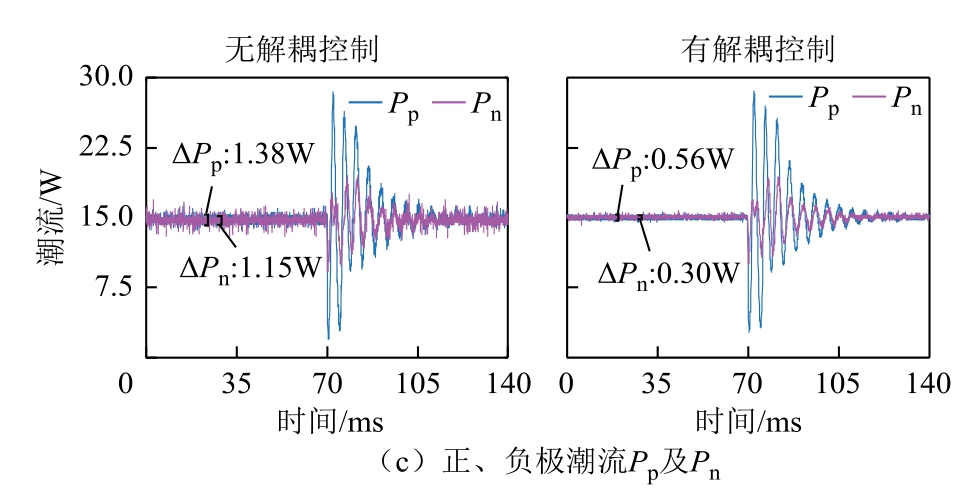
图20 恒功率本地负载有、无解耦控制的实验结果
Fig.20 Experimental results of local CPL with/without decoupling control strategy
5 结论
本文提出了一种基于TAB-PFC 的环形双极直流配电网不平衡潮流抑制策略,可实现灵活调节线路潮流,同时减小线路损耗,提高系统控制的灵活性和运行效率,得到以下结论:
1)TAB-PFC 通过改变串入线路中的电压,可增加环形双极直流配电网控制的自由度。此外,还可抑制由受端电压、新能源出力等不平衡引起的配电网的不平衡潮流。
2)由于存在中线电阻,环形双极直流配电网中TAB-PFC 的控制与输出变量之间存在耦合。通过引入解耦控制矩阵,实现输入和输出之间的近似解耦。
3)所提的解耦控制方法简单易行,为各个控制闭环的独立设计奠定了基础,可有效提高潮流控制的动态性能。
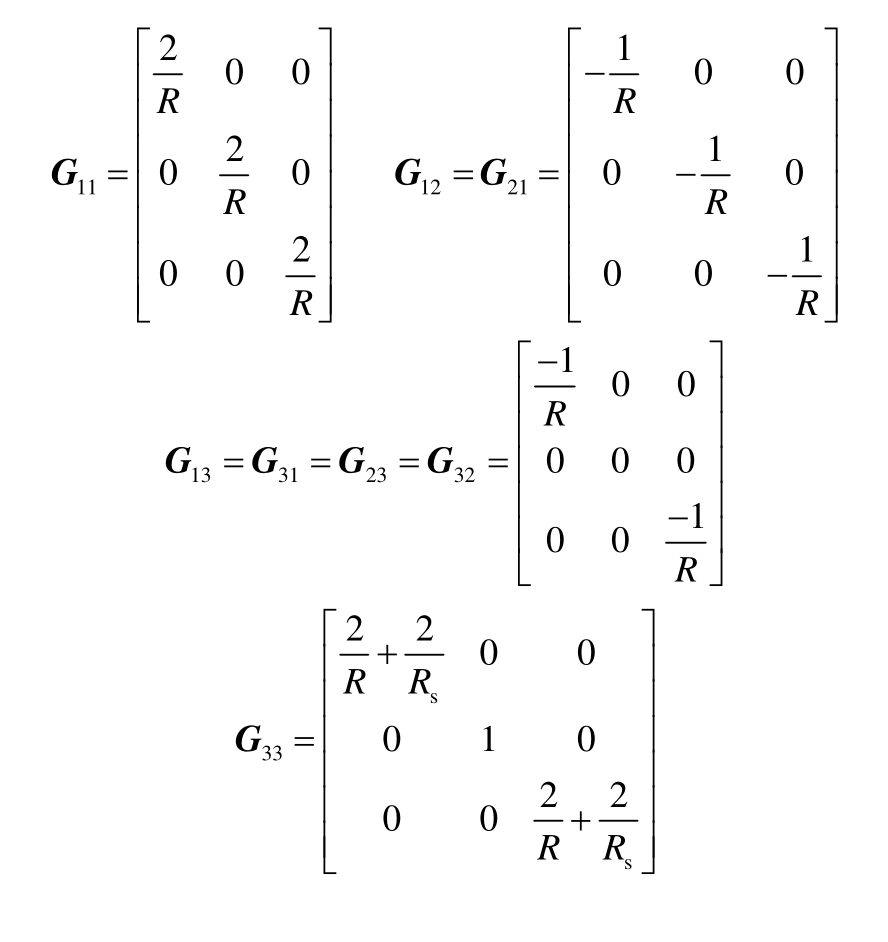
附 录

[1]李馨雨,吕煜,许建中.具备故障限流功能的新型线间直流潮流控制器[J].电力系统自动化,2020,44(21):80-88.
Li Xinyu,Lü Yu,Xu Jianzhong.Interline DC power flow controller with fault current limiting function [J].Automation of Electric Power Systems,2020,44(21):80-88.
[2]廖建权,周念成,王强钢,等.直流配电网电能质量指标定义及关联性分析[J].中国电机工程学报,2018,38(23):6847-6860,7119.
Liao Jianquan,Zhou Niancheng,Wang Qianggang,et al.Definition and correlation analysis of power quality index of DC distribution network[J].Proceedings of CSEE,2018,38(23):6847-6860,7119
[3]Tan D.Structured microgrids (SμGs) and flexible electronic large power transformers (FeLPTs)[J].CES Transactions on Electrical Machines and Systems,2020,4(4):255-263.
[4]李幸芝,韩蓓,李国杰,等.考虑非高斯耦合不确定性的交直流配电网两阶段概率状态估计[J].电工技术学报,2020,35(23):4949-4960.
Li Xingzhi,Han Bei,Li Guojie,et al.Two-stage probabilistic state estimation for AC/DC distribution network considering non-Gaussian coupling uncertainties[J]. Transactions of China Electrotechnical Society,2020,35(23):4949-4960.
[5]王浩翔,赵冬梅,陶然,等.基于分解的多目标进化算法的含MMC-HVDC 交直流混合系统最优潮流研究[J].电工技术学报,2020,35(17):3691-3702.
Wang Haoxiang,Zhao Dongmei,Tao Ran,et al.Study on optimal power flow for AC/DC hybrid system incorporating MMC-HVDC based on MOEA/D[J].Transactions of China Electrotechnical Society,2020,35(17):3691-3702.
[6]许烽,徐政,刘高任.新型直流潮流控制器及其在环网式直流电网中的应用[J].电网技术,2014,38(10):2644-2650.
Xu Feng,Xu Zheng,Liu Gaoren.A neotype of DC power flow controller and its applications in meshed DC grids[J].Power System Technology,2014,38(10):2644-2650.
[7]姚良忠,崔红芬,李官军,等.柔性直流电网串联直流潮流控制器及其控制策略研究[J].中国电机工程学报,2016,36(4):945-952.
Yao Liangzhong,Cui Hongfen,Li Guanjun,et al.Studies of series DC power flow controller and its control strategy in the VSC based DC grid[J].Proceedings of the CSEE,2016,36(4):945-952.
[8]李国庆,边竞,王鹤,等.适用于直流电网的环流式线间直流潮流控制器[J].电工技术学报,2020,35(5):1118-1127.
Li Guoqing,Bian Jing,Wang He,et al.A circulating current interline DC power flow controller for DC grid[J].Transactions of China Electrotechnical Society,2020,35(5):1118-1127.
[9]武文,吴学智,荆龙,等.适用于多端直流输电系统的模块化多端口直流潮流控制器[J].电工技术学报,2019,34(3):539-551.
Wu Wen,Wu Xuezhi,Jing Long,et al.A modular multi-port DC power flow controller for multiterminal DC transmission system[J].Transactions of China Electrotechnical Society,2019,34(3):539-551.
[10]Zhong Xu,Zhu Miao,Chi Yongning,et al.Composite DC power flow controller[J].IEEE Transactions on Power Electronics,2020,35(4):3530-3542.
[11]Gomid-Bellmunt O,Sau-Bassols J,Prieto-Araujo E,et al.Flexible converters for meshed HVDC grids:from flexible AC transmission systems (FACTS) to flexible DC grids[J].IEEE Transactions on Power Delivery,2020,35(1):2-15.
[12]Jovcic D,Hajian M,Zhang H,et al.Power flow control in DC transmission grids using mechanical and semiconductor based DC/DC devices[C]//The 10th IET International Conference on AC and DC Power Transmission,Birmingham,UK,2012:1-6.
[13]Mu Qing,Liang Jun,Li Yalou,et al.Power flow control devices in DC grids[C]//2012 IEEE Power and Energy Society General Meeting,San Diego,USA,2012:1-7.
[14]Hertem V D,Verboomen J,Purchala K,et al.Usefulness of DC power flow for active power flow analysis with flow controlling devices[C]//The 8th IEEE International Conference on AC and DC Power Transmission,London,UK,2006:58-62.
[15]Balasubramaniam S,Ugalde-Loo C E,Liang J,et al.Experimental validation of dual H-bridge current flow controllers for meshed HVDC grids[J]IEEE Transactions on Power Delivery,2018,33(1):381-392.
[16]Cheng Danni,Zou Jianlong.Power flow calculation method of DC grid with interline DC power flow controller (IDCPFC)[C]//2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC),Macao,China,2019:1-5.
[17]Chen Wu,Zhu Xu,Yao Liangzhong,et al.An interline DC power-flow controller (IDCPFC) for multiterminal HVDC system[J].IEEE Transactions on Power Delivery,2015,30(4):2027-2036.
[18]Sau-Bassols J,Prieto-Araujo E,Gomis-Bellmunt O,et al.Series interline DC/DC current flow controller for meshed HVDC grids[J].IEEE Transactions on Power Delivery,2018,33(2):881-891.
[19]Jovcic D.Bidirectional,high-power DC transformer[J].IEEE Transactions on Power Delivery,2009,24(4):2276-2283.
[20]Rouzbehi K,Heidary Y S S,Shariati M N.Power flow control in multi-terminal HVDC grids using a serialparallel DC power flow controller[J].IEEE Access,2018(6):56934-56944.
[21]Purgat P,Mackay L,Qin Z,et al.On the protection of the power flow control converter in meshed low voltage DC networks[C]//2018 IEEE Energy Conversion Congress and Exposition(ECCE),Portland,USA,2018:478-484.
[22]Purgat P,Mackay L,Schulz M,et al.Design of a power flow control converter for bipolar meshed LVDC distribution grids[C]//2018 IEEE 18th International Power Electronics and Motion Control Conference,Budapest,Hungary,2018:1073-1078.
[23]廖建权,周念成,王强钢.辐射型双极直流配电网不平衡电压分析及抑制[J].中国电机工程学报,2019,39(18):5380-5388,5585.
Liao Jianquan,Zhou Niancheng,Wang Qianggang.Analysis and suppression of unbalanced voltage in radiant bipolar DC distribution network[J].Proceedings of the CSEE,2019,39(18):5380-5388,5585.
[24]Liao Jianquan,Zhou Niancheng,Huang Yuansheng,et al.Unbalanced voltage suppression in a bipolar DC distribution network based on DC electric springs[J]. IEEE Transactions on Smart Grid,2020,11(2):1667-1678.
[25]唐巍,李天锐,张璐,等.基于三相四线制最优潮流的低压配电网光伏-储能协同控制[J].电力系统自动化,2020,44(12):31-40.
Tang Wei,Li Tianrui,Zhang Lu,et al.Coordinated control of photovoltaic and energy storage system in low-voltage distribution networks based on threephase four-wire optimal power flow[J].Automation of Electric Power Systems,2020,44(12):31-40.
[26]Vuyyuru U,Maiti S,Chakraborty C.Active power flow control between DC microgrids[J]IEEE Transactions on Smart Grid,2019,10(5):5712-5723.
[27]Ericson R W,Maksimovic D.Fundamentals of power electronics[M]. Secaucus: Kluwer Academic Publishers,2000.
[28]Van der Blij N H,Ramirez-Elizondo L M,Spaan M T J,et al.Symmetrical component decomposition of DC distribution systems[J].IEEE Transactions on Power Systems,2018,33(3):2733-2741.
[29]Zhao C,Round S D,Kolar J W.An isolated three-port bidirectional DC-DC converter with decoupled power flow management[J].IEEE Transactions on Power Electronics,2008,23(5):2443-2453.
[30]黄远胜,刘和平,苗轶如,等.基于并联虚拟电阻的级联DC-DC 变换器稳定控制方法[J].电工技术学报,2020,35(18):3927-3937.
Huang Yuansheng,Liu Heping,Miao Yiru,et al.Cascaded DC-DC converter stability control method based on paralleling virtual resistor[J].Transactions of China Electrotechnical Society,2020,35(18):3927-3937.