0 引言
腐蚀减薄和裂纹是石油、化工、核电等领域大口径厚壁管道失效事故的主要诱因。对这两类缺陷同时进行检测,对于管道内在线监测和可靠性评估具有重要意义[1-2]。横波电磁超声换能器(Electromagnetic Acoustic Transducer,EMAT)在检测金属厚度时具有较高的灵敏度[3-4],而且与压电超声相比,EMAT 具有无需耦合剂、无需对试件表面进行预处理的特性,可用在高温、在线等恶劣环境[5-9],适合于管道检测[10]。
国内外学者在横波电磁超声单独测厚或缺陷检测方面已有不少研究。目前测厚研究主要集中在优化参数、提高换能效率方面。文献[11]提出一种轴对称多磁体结构来增强横波EMAT 的偏置磁场,提高了横波模式纯度和信号强度并用于厚度检测。文献[12]采用正弦波对横波电磁超声换能器进行激励,分析了频率脉宽和提离距离对钢板测厚的影响,结果表明当激励频率和EMAT 固有频率相同时其换能效率最高。文献[13]通过正交试验对横波EMAT的线圈进行优化,指出激励电流的频率和线圈的尺寸对横波的传播特性有明显影响。文献[14]分析了多层螺旋线圈横波EMAT 的参数对换能效率和横波纯度的影响,并给出了最佳参数组合。文献[15]采用三通道EAMT,研制了一种用于管道内检测的电磁超声在线测厚系统,测厚范围达8~35mm。文献[16]利用线性调频脉冲激励换能器,把脉冲压缩处理技术应用到EMAT 测厚中,增大了接收信号的信噪比。
以上测厚方法在单独测厚方面取得了较好效果,其采用的垂直入射的脉冲回波模式,也常用于检测平行于检测面的缺陷(如夹层、折叠等),但无法有效检测与检测面垂直的裂纹。文献[17]建立了厚铝板底部面状缺陷、收发一体横波EMAT 的二维有限元模型,利用正交试验对磁铁和线圈结构参数进行优化后,缺陷回波信号的幅值得到了提高。文献[18]指出,对于开口宽度远小于波长的底面裂纹缺陷,垂直入射横波的反射能量低,故无法检测垂直裂纹。
常规检测垂直裂纹缺陷的方法是横波斜射法。文献[19]开发了基于电磁超声斜入射横波的厚壁管道裂纹检测系统,对裂纹进行有效检测。文献[20]提出基于EMAT 斜入射SH 波的厚壁管道检测方法,对厚壁管道内壁不同深度的裂纹进行检测。文献[21]提出了通过测量几个斜角入射横波反射到达时间确定裂纹状缺陷大小的方法。文献[22]分析了腐蚀形成的小倾角斜面裂纹缺陷对电磁超声横波的影响,指出横波电磁超声换能器在斜面缺陷测量中产生误差的原因是斜面反射回波产生的声时差异。虽然横波斜射法可以方便地检测与检测面垂直的裂纹,但倾斜入射方式无法检测材料厚度。
因此,常规的垂直入射的横波换能器在测厚时具有较高灵敏度,但检测垂直裂纹时,需要更换斜入射波的探头,单个换能器无法同时进行这两种检测。这不仅增加了检测成本,而且检测效率低,不利于在线监测。
复合检测是实现厚度和裂纹缺陷同时检测的有效途径。文献[23]提出将电磁超声与涡流检测相结合,在利用电磁超声测厚的同时,通过线圈拾取漏磁和涡流信息,实现了对管道裂纹缺陷的检测。文献[24]将超声测厚和导波检测相结合,提出一种螺旋型和回折型线圈的复合式电磁超声换能器,采取硬件分时复用的方式实现了定点超声横波测厚与周向Lamb 波对管道缺陷的一次性快速扫查,取得了较好的效果。然而上述两种方法适合于薄壁结构的测厚和裂纹缺陷的检测,无法对厚壁结构进行检测。
因此,需要研究设计新的电磁超声换能器,以满足同时检测厚壁管道结构的厚度和裂纹的需要。
针对上述问题,本文采用复合检测思路,利用横波EMAT 方向性好、穿透能力强的优点,结合线圈设计的灵活性,设计了一种正交横波EMAT。该换能器同时激发两个垂直入射的正交偏振横波,利用反射波幅值的差异与横波偏振方向的关系,通过一次检测同时进行测厚、裂纹及裂纹方向的检测。与常规横波斜入射检测裂纹的方法不同之处在于,该方法通过垂直入射的两个正交横波既可检测垂直裂纹,还可解决现有复合导波换能器无法有效进行厚壁底面裂纹检测问题。
本文采用有限元软件对该换能器声场和激发过程进行三维建模仿真,分析了线圈间距、裂纹尺寸对于正交横波声场的影响,通过实验验证正交偏振横波EMAT 同时进行测厚和裂纹检测的可行性。
1 正交横波EMAT 工作原理
1.1 正交横波EMAT 换能机理
相对于大口径管道结构,换能器尺寸较小,可将检测简化为平板测厚和底面裂纹检测。正交偏振横波EMAT 示意图如图1 所示。图1 中,正交偏振横波EMAT 包含两个正交的蝶形线圈A 和B,置于永磁体底部,线圈A 位于线圈B 的下方。换能器的有效孔径为线圈中心处的正方形区域(两个线圈中间的垂直和水平交叉部分)。铝板中,产生电磁超声的主导因素是洛仑兹力。由于永磁体的垂直磁场穿过该区域,该区域下方试件趋肤层内的质点受到平行于xOy 平面的洛仑兹力。

图1 正交偏振横波EMAT 示意图
Fig.1 Schematic of the orthogonal EMAT
当蝶形线圈A 中通入高频电流时,材料的表面会感应出与线圈电流方向相反的感应涡流,感应涡流在静态偏置磁场和交变磁场的作用下产生洛仑兹力,使趋肤层质点发生水平(x 轴)方向的高频振动,产生一个x 轴方向偏振的横波。同理,蝶形线圈B(相对线圈A 旋转90˚)通入高频电流时,由于洛仑兹力作用质点发生沿y 轴方向的振动,产生具有y 轴方向偏振的附加横波,这样便形成了一对正交偏振横波,如图1b 所示。
平行于x 轴和平行于y 轴的洛仑兹力大小可以简化为[8]
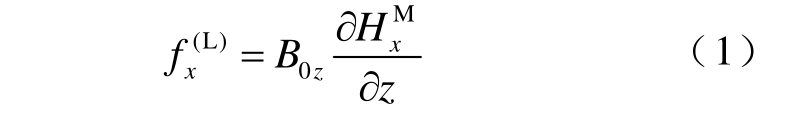
式中,fx(L)为平行于x 轴的洛仑兹体积力;fy(L)为平行于y 轴的洛仑兹体积力;B0z 为垂直于试件表面的磁感应强度;HxM、HyM 分别为试件内的磁场强度x方向分量和y 方向分量。![]() 分别产生x 方向偏振的横波和y 方向偏振的横波。
分别产生x 方向偏振的横波和y 方向偏振的横波。
当线圈尺寸小于永磁体时,涡流区域的磁感应强度x 方向、y 方向分量B0x、B0y 较小,所以传感器产生的纵波能量相比横波很小,检测中可以忽略纵波的影响。
正交偏振横波从表面垂直射入铝板,沿厚度方向(z 轴)传播,经底面反射后,回波信号由收发一体的EMAT 接收,接收过程是上述过程的逆过程。
此外,一般情况下,当两个接近的线圈同时通入高频脉冲激励时,线圈间互感引起的相互干扰不容忽视。而本文的正交线圈中,当线圈A 通入高频电流iA 时,在线圈A 中间导线两侧矩形框内的磁链方向相反。而线圈B 相对线圈A 旋转90˚,交链到线圈B 中间导线两侧矩形框内的互感磁链ΨBA,正负抵消。可知,线圈A 与线圈B 的互感MBA=ΨBA/iA=0。互感电动势和互感电流也为0,两个线圈相互不干扰。实验中的EMAT 两个正交线圈有一定宽度,使得互感磁链不能完全抵消,但高频互感非常小,两个线圈相互作用可忽略不计。
1.2 正交横波EMAT 厚度和裂纹检测基本原理
洛仑兹力f L 作用下铝板中质点运动方程为
式中,G、κ为拉梅常数;u 为位移;ρ 为体密度。
设fx(L)、fy(L)激励的两列沿z 轴垂直入射的正交线性偏振横波为ux(z,t)、uy(z,t)。与铝板底部裂纹作用后并经后壁反射的反射波为![]() 。底部裂纹与y 轴的夹角为θN,铝板上表面到后壁距离为L,如图2 所示。
。底部裂纹与y 轴的夹角为θN,铝板上表面到后壁距离为L,如图2 所示。
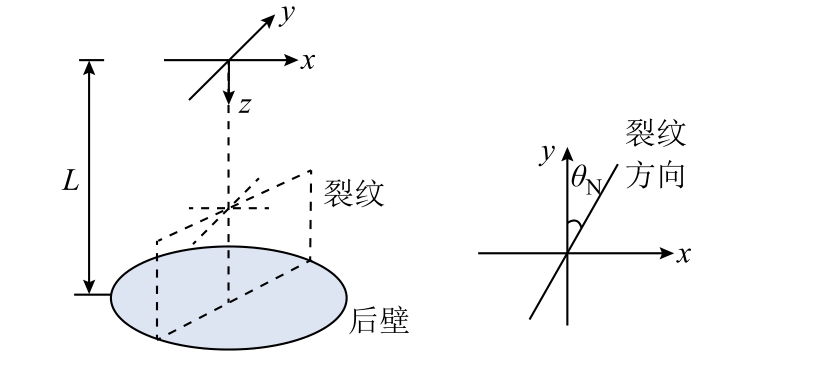
图2 正交偏振横波测厚和裂纹检测示意图
Fig.2 Schematic of orthogonal shear waves for thickness measurement and crack detection
为简化分析,假设入射偏振横波均是初相位为0˚的简谐波,且传播中无衰减,则

式中,A0 为振幅;λ 为波长。
由横波偏振原理可知,当 0≤θN≤90˚时,反射波。

式中,Mx、My 为反射波幅值。

式(10)为两个正交偏振横波的反射回波幅值之差与裂纹角度的关系。
特别地,当θN=0˚时,垂直于y 轴的横波ux(z,t)无法通过裂纹,后壁反射波幅值Mx=0,而平行于y轴的横波uy(z,t)则穿过裂纹,后壁反射波幅值My=A0。
同理,当θN=90˚时,Mx=A0,My=0。
当无裂纹时,Mx=A0,My=A0。
由此可见,两个垂直入射的正交偏振横波的反射回波幅值可以用于检测底部裂纹状缺陷的存在及裂纹的方向,同时,通过计算垂直入射横波回波信号的飞行时间(Time of Flight,ToF)进行厚度测量,以实现厚度和裂纹的同时检测。
2 正交横波EMAT 仿真分析
2.1 正交横波EMAT 模型
为了研究两个正交偏振的横波的声场分布以及与裂纹缺陷的相互作用,采用多物理场仿真软件Comsol Multiphics 建立正交横波电磁超声换能器三维有限元模型如图3 所示。该模型由永磁体、线圈A、线圈B、铝板、空气组成(图中略去了空气场)。
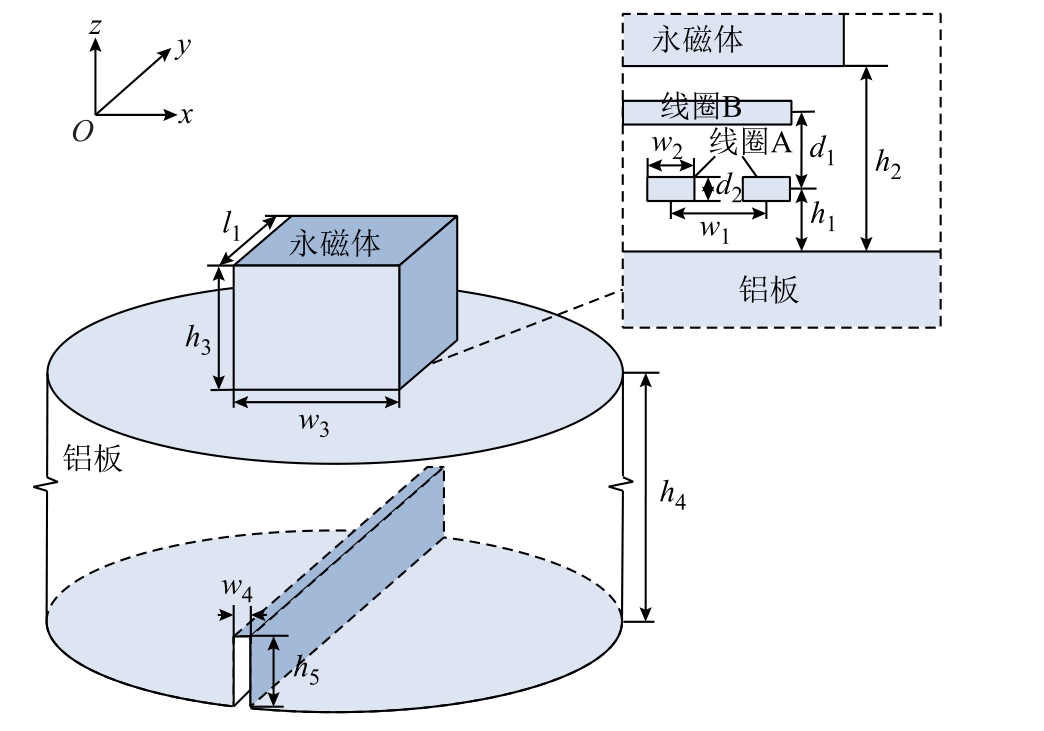
图3 EMAT 的三维有限元模型示意图
Fig.3 Schematic of 3D FE for EMAT
为简化计算,只对线圈的有效检测区域进行建模,蝶形线圈A、B 简化为相互垂直的12 根直导线。线圈A 的导线平行于y 轴,关于y 轴对称且等间距分布。线圈B 的导线平行于x 轴,关于x 轴对称且等间距分布。永磁体为方形钕铁硼磁铁。两个线圈采用双层印制电路板(Printed Circuit Board,PCB)工艺设计。
为了研究不同角度的裂纹对声场的影响,需要保证铝板侧面边界关于z 轴对称,故试件设置为圆柱形。同时为避免侧面反射对波形的影响,圆柱侧面设置为低反射边界条件。在铝板底部设置一个长为12mm、宽为0.5mm、高为5mm 的矩形槽口来模拟裂纹缺陷,改变裂纹与线圈夹角来模拟裂纹的方向。
线圈A、B 中的激励电流采用频率为1MHz、峰值为20A 和周波数为3 的Tone-burst 信号,EMAT仿真模型参数见表1。
表1 EMAT 仿真模型参数
Tab.1 Parameters of EMAT simulation model

(续)

由于EMAT 接收是激发的逆过程,线圈A 产生横波的偏振方向平行于x 轴,线圈B 产生横波偏振方向平行于y 轴,故在线圈有效检测区下方铝板内选取点M(0 mm,0 mm,-0.1mm),通过该点沿不同方向的归一化位移分量来模拟EMAT 不同偏振方向的回波接收,即用位移场u 分量代表线圈A 的接收信号,位移场v 分量代表线圈B 的接收信号。
2.2 仿真结果与分析
2.2.1 正交横波EMAT 声场与裂纹的相互作用
对于底面无裂纹的完好铝板,正交横波EMAT两个线圈A、B 产生的横波仿真结果如图4a 所示,图为M 点的位移u、v 分量的归一化幅值信号。从图4 可以看出,u、v 分量的归一化值完全相同。

图4 M 点的位移场u、v 分量的归一化值
Fig.4 Normalized time-trace of u and v components of the displacement at point M
由两个波峰值的ToF 计算得出超声波的速度为2 920m/s,与横波理论声速3 121m/s 的相对误差约为6%。通过更细的网格剖分可减小误差但会大幅增加仿真时长。通过声速对比可知两个相互正交的蝶形线圈产生的超声波是两个沿厚度方向传播的横波。
对于底面含裂纹缺陷的铝板,当裂纹面与x 轴垂直时(设此时裂纹方向角为0˚),线圈A 产生的横波偏振方向与裂纹面垂直,线圈B 的横波偏振方向与裂纹面平行,M 点的归一化幅值信号如图4b 所示。位移v 分量的幅值与无裂纹时信号幅值相比没有变化,ToF 也无变化;而u 分量ToF 无变化,但幅值为 0.05(pu),降低至约为无裂纹时信号幅值0.33(pu)的15%。
底面含裂纹铝板反射回波位移场云图如图5 所示。从位移场云图看,对于底面无裂纹的铝板,位移场u、v 分量云图基本相同。而对于底面含裂纹的铝板,xOz 截面上位移场u、v 分量的云图(t=11.5μs时)差异很大。

图5 底面含裂纹铝板反射回波位移场云图
Fig.5 Displacement component of the reflected shear waves when the back-wall has a notch in it
结合图4、图5 分析得:①由于线圈A 产生的入射横波偏振方向与裂纹面垂直,反射回波位移的u 分量在裂纹处发生了很大的散射,导致幅值降低,而线圈B 产生的横波偏振方向与裂纹面平行,反射回波位移的v 分量几乎不受裂纹的影响。②底面裂纹造成了两个正交线圈回波信号时域幅值差异很大,而ToF 不变。因此,利用ToF 测量厚度的同时,可以通过两线圈回波幅值差判断裂纹存在。
进一步分析裂纹方向对线圈回波信号幅值的影响。设裂纹面与A 线圈的夹角为θ,则与B 线圈的夹角为90˚-θ,θ 取值0~90˚,步进角度为5˚进行仿真,图6 为θ 分别取值0˚、30˚、90˚时位移场u 分量的归一化值。可见θ 取值变化时,回波信号u 分量的ToF 不变,而幅值随着θ 取值的变化而变化。
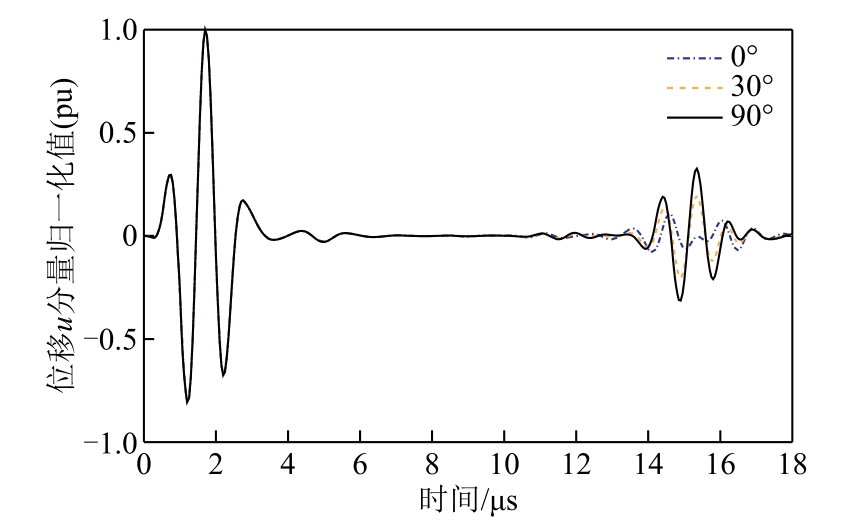
图6 位移场u 分量的归一化值(θ=0˚,30˚,90˚)
Fig.6 Normalized time-trace of u component of the displacement(θ=0˚,30˚,90˚)
通过位移u、v 分量幅值差归一化值随裂纹方向变化来考察A、B 线圈的反射回波信号的幅值差与裂纹方向的关系。仿真结果如图7 所示。当0<θ<45˚时,v 分量幅值大于u 分量幅值,且两者幅值差的绝对值随着θ 的增大而减小;当45˚<θ<90˚时,v 分量幅值小于u 分量幅值,且幅值差的绝对值随着θ 的增大而增大。在θ=45˚附近,两者幅值差约等于0。
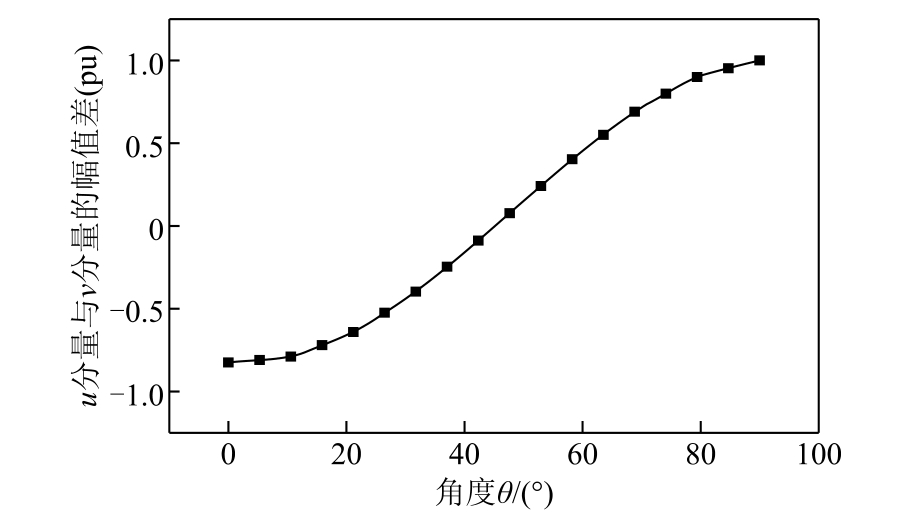
图7 u、v 分量幅值差归一化值与裂纹角度θ 的关系
Fig.7 Amplitude difference of u and v components vs.θ
由仿真可得,u 分量与v 分量的幅值差与裂纹方向呈现单调的规律性关系,这与1.2 节中推导的关系式(式(10))基本吻合。可以根据A、B 线圈的反射回波信号的幅值差与θ 的对应关系,来确定裂纹的方向。
2.2.2 正交EMAT 声场的对称性
由第1 节可知,裂纹检测和裂纹角度的确定依赖A、B 的相对幅值差。然而该幅值差受到A、B 线圈产生声场的对称性的影响。尽管两个正交线圈在无裂纹铝板中接收的信号归一化值相同(幅值差为0),而实际上线圈间距的存在使得两个线圈提离距离不同,激发的正交横波声场和幅值有所不同。声场对称性对于减小检测误差非常重要,有必要分析声场的对称性及影响因素。
分析正交线圈声场的对称性。线圈间距(A、B线圈沿z 轴方向的间距)d1=0.3mm 时,考察质点位移场分布。过M 点做与铝板表面平行的截面(z= -0.1mm)。图8 为t=2.2μs 时截面上质点位移云图。由图8 可知,位移场关于与x 轴正向夹角为135˚的直线基本呈对称分布。

图8 z=-0.1mm 截面位移场云图
Fig.8 Distribution of displacement amplitude field (z=-0.1mm)
考察线圈间距对声场对称性的影响。保持线圈A 提离距离不变,设置线圈间距d1(也即双层电路板厚度)分别为0.3mm、0.4mm、0.5mm、0.6mm、0.7mm 进行仿真,截面内以M 点为中心半径R=4mm的圆上各质点在t=2.2μs 时刻总位移归一化分布线如图9 所示。d1 越小,两个横波偏振的合成方向越接近 135˚对称轴。d1=0.3mm 的对称程度最好,d1=0.7mm 的对称性最差。

图9 截面圆周上各质点总位移分布线图
Fig.9 Line diagram of the normalized displacement on the circle(R=4mm,z=-0.1mm)
提取d1=0.3mm,0.4mm,0.5mm,0.6mm,0.7mm时M 点处的位移场的u 分量和v 分量,两者幅值差与线圈间距的关系如图10 所示。可见两个正交偏振横波的幅值差随着两个线圈间距增大而增大。减小线圈间距可以减小回波幅度差,提高正交横波声场的对称性,减小检测误差。
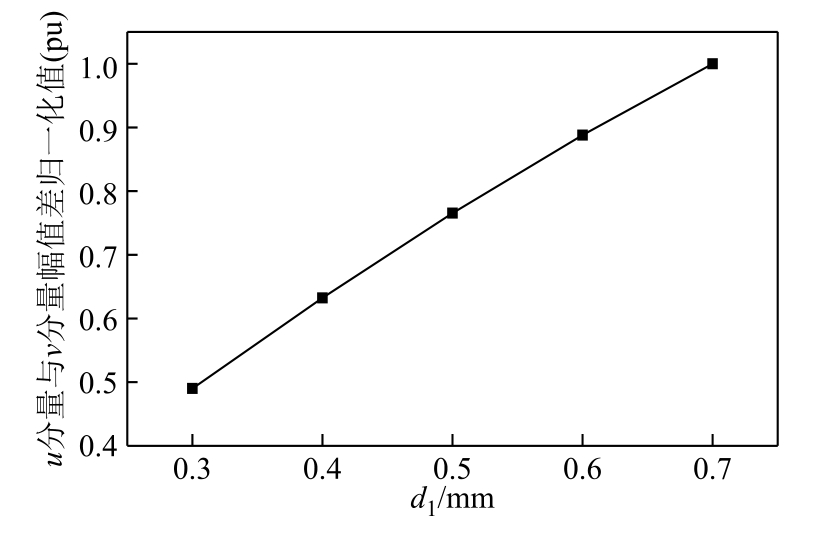
图10 u、v 分量幅值差归一化值与d1 的关系
Fig.10 Amplitude difference of u and v components vs.d1
2.2.3 裂纹尺寸对正交EMAT 声场的影响
由正交横波检测方法可知,裂纹的检测取决于u、v 分量幅值关系。然而裂纹尺寸(深度、长度、宽度)变化会影响反射回波u、v 分量幅值。设置裂纹方向与线圈B 波束偏振方向保持平行,即角度设置为0˚。分别改变裂纹深度、宽度、长度三个参数之一,保持另外两者不变,进行三组仿真:①裂纹深度取值0~6mm,步长0.5mm;②长度取值0~3d,步长0.25d,d 为换能器孔径,d=4mm;③宽度取值0.1~1mm,步长0.1mm;仿真结果如图11~图13 所示。
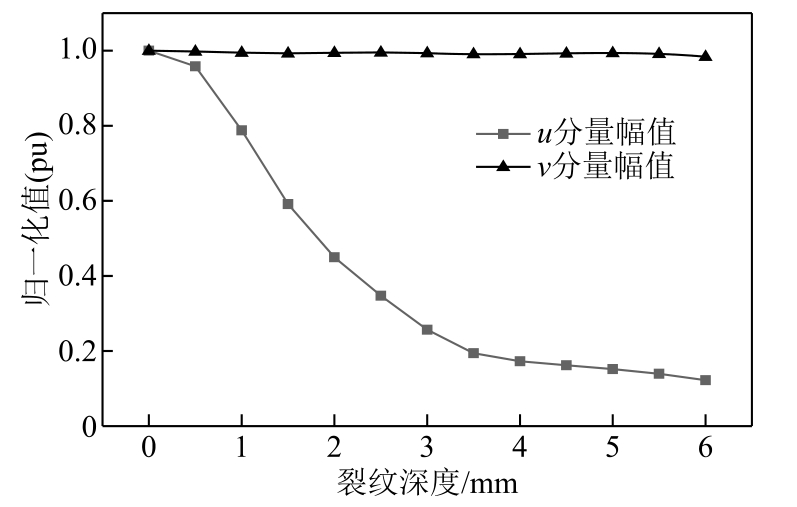
图11 u、v 分量幅值与裂纹深度的关系
Fig.11 Amplitude of u and v components vs.crack depth

图12 u、v 分量幅值与裂纹长度的关系
Fig.12 Amplitude of u and v components vs.crack length

图13 u、v 分量幅值与裂纹宽度的关系
Fig.13 Amplitude of u and v components vs.crack width
以完好铝板反射波幅值为参考,裂纹深度与反射回波归一化幅值的关系如图11 所示。仿真结果表明,裂纹深度从0~4mm 逐渐增大时,反射回波信号v 分量幅度基本不变,而u 分量幅度明显减小,两者幅值差明显增大。当裂纹深度大于4mm 时,反射回波信号幅值差基本趋于稳定。
反射波幅值还受到裂纹长度的影响。图12 为仿真得到的裂纹长度与反射回波幅值的关系曲线。结果表明,当裂纹长度从0~2d 逐渐增大时,v 分量基本不变,u 分量幅度明显下降。裂纹长度增加使得偏振横波与裂纹的相互作用逐渐增强,导致u 分量幅值减小。当裂纹长度大于2d 时,回波信号幅值趋于稳定。
图13 为0.1~1mm 的裂纹宽度与反射回波幅度的关系曲线。从总体看,裂纹宽度变化对反射回波幅度影响较小,且v 分量、u 分量保持较大的幅值差。当宽度接近1mm 时,反射波幅值均略有所下降。原因是裂纹宽度增大使得裂纹顶部的波的散射增大。
3 正交横波EMAT 同时检测厚度和裂纹
3.1 正交横波EMAT 实验平台
本文提出的正交偏振EMAT 线圈采用FPC 柔性电路板(双层板,厚度为0.2mm)工艺制备,A 线圈位于底层,B 线圈位于顶层。另外还制作了厚度为0.4mm、0.6mm、0.8mm 的PCB 双层电路板,以研究线圈间距对检测信号的影响。正交EMAT 线圈实物如图14 所示。不同厚度的双面电路板中线圈A、B 的导线铜厚度无变化,均为0.035mm。

图14 正交EMAT 线圈实物图
Fig.14 Orthogonal EMAT coils
实验试件:参考GB/T 33888—2017《超声测厚仪特性与验证》[25]制备用于测厚和裂纹检测的实验试件,制备的完好试件和含底面裂纹试件均为厚50mm、直径150mm 的铝合金试件,其中,裂纹通过在试件底面开槽口来模拟,分别制备了深度不同的裂纹试件。底面槽深分别为0.5mm、1mm、3mm、5mm,宽0.5mm,长150mm(沿直径贯穿底面)。设置裂纹初始方向与线圈B 偏振方向平行。
实验系统如图15 所示,该系统由Ritec RAM-5000 产生两个1MHz、周波数为2 的高频脉冲电流激励信号,从两个输出通道输出,经阻抗匹配后,分别施加在线圈A、B 上。示波器采集经滤波放大后的感应电压信号,采用脉冲回波法,验证正交偏振横波EMAT 换能器检测铝板厚度和缺陷的有效性。

图15 正交横波EMAT 检测实验平台
Fig.15 Measurement setup of the orthogonal EMAT
3.2 实验结果与分析
实验中,正交EMAT 的两个线圈A、B 感应出的原始回波电压信号较为微弱,信噪比很低,仅凭硬件难以完全滤除噪声。因此对原始回波信号进行小波包去噪(四层分解)处理。图16 为完好铝板上A 线圈接收的原始回波信号去噪后的时域波形,可见大部分噪声被滤除,信噪比有效提高。由于第1反射回波信号受到主冲击脉冲干扰,因此本文实验中取第2、3 反射回波信号进行分析。

图16 EAMT 接收的反射回波信号(A 线圈)
Fig.16 Back-wall reflection recorded with A coil
将换能器分别放置在完好铝板和底面含裂纹铝板上进行实验,图17a、图17b 分别为完好铝板、含底面裂纹铝板上A、B 线圈接收的回波信号。

图17 EAMT A、B 线圈接收的反射回波信号
Fig.17 Back-wall reflection recorded with the coils of A and B
3.2.1 厚度测量
用游标卡尺进行3 次测量求平均值,分别得到完好铝板的厚度为50.25mm,含底面裂纹铝板厚度为50.17mm。用完好铝板的厚度除以完好铝板相邻回波信号峰值点对应的ToF 值,得到横波在铝板中的传播速度。A 线圈的相邻回波峰值点对应的ToF值为32.14μs,计算得横波的传播速度为3 127m/s。B 线圈的相邻回波峰值点对应的ToF 值为32.12μs,计算得到横波的传播速度为3 129m/s。横波的波速理论值为3 121m/s,实验值和理论值基本相符,由换能器两个线圈A、B 产生的超声波均为横波。
以线圈A、B 在完好铝板中测得的波速为基准,根据含底面裂纹铝板的回波信号的ToF 值,即可得到A、B 线圈测量的含裂纹铝板的厚度值。测得的含底面裂纹铝板的波速和厚度见表2。
表2 厚度测量
Tab.2 Thickness measurement

从表2 中可以看出,用正交偏振横波EMAT 的两个线圈A、B 对含底面裂纹试件进行厚度测量时,线圈A 的测量结果与游标卡尺的测量结果相比,相对误差为0.2%,线圈B 相对误差0.28%。线圈B 比线圈A 的相对误差稍大。造成差异的原因可能是实验过程中随机波动误差。
3.2.2 裂纹检出和裂纹方向的检测
从图17a 得出,对于完好铝板,A、B 线圈的反射回波信号幅值基本相同,二者幅值差为6.74mV。差异是由板厚引起提离距离略微不同导致的。
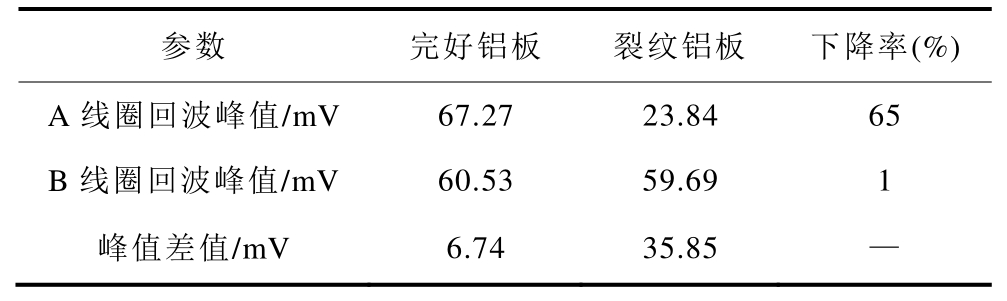
而对于含裂纹缺陷的铝板,从图17b 可得,A线圈反射回波信号峰值相对于B 线圈产生了明显下降。比较A、B 两个反射回波信号的峰值见表3,二者幅值差为35.85mV。相较于完好试件,A 线圈信号幅值下降65%,B 线圈信号幅值下降1%。实验表明,底面裂纹造成的两个正交线圈回波信号幅值差异很大,可据此判定是否存在底面裂纹。
表3 A、B 线圈反射回波信号的峰值
Tab.3 Amplitude of reflection recorded with the coils
进一步地,为了验证裂纹方向(裂纹与换能器的相对角度θ)与回波信号幅值的关系,实验中,通过旋转换能器来改变θ 的大小,每间隔10˚检测并提取A、B 线圈反射回波信号的幅值。实验结果如图18 所示。当0<θ<45˚时,A 线圈的反射回波幅值小于B 线圈回波幅值;当45˚<θ<90˚时,A 线圈的反射回波幅值大于B 线圈回波幅值。在45˚附近,A、B 线圈反射回波幅值相差不明显。实验结果说明,A、B 线圈的反射回波信号的幅值差与裂纹方向角θ呈现单调的规律性关系。根据A、B 线圈的反射回波信号的幅值差能够确定裂纹的方向。

图18 A、B 线圈信号幅值差与裂纹角度θ 的关系
Fig.18 Amplitude difference of signal of A and B coils vs.θ
通过上述实验,验证了正交EMAT 同时测量厚度和检测裂纹,并确定裂纹方向的方法是可行的,即通过正交线圈回波信号的ToF 进行厚度测量的同时,利用两个线圈回波幅值差可判定试件底面是否存在裂纹(幅值差较大时试件底面存在裂纹),并且根据幅值差与θ 的关系曲线可以确定裂纹方向。
3.2.3 线圈间距对正交声场对称性的影响
A、B 线圈在完好铝板中的回波信号幅值差能够反映声场的对称性,因此分析板厚与A、B 线圈信号幅值差的关系。利用制作的厚度为 0.2mm、0.4mm、0.6mm、0.8mm 的电路板,采用脉冲回波法在完好铝板上进行实验,得到A、B 线圈的回波信号幅值差与板厚的关系见表4。
表4 A、B 线圈信号幅值差与板厚
Tab.4 Amplitude difference of signal of A and B coils vs.d1
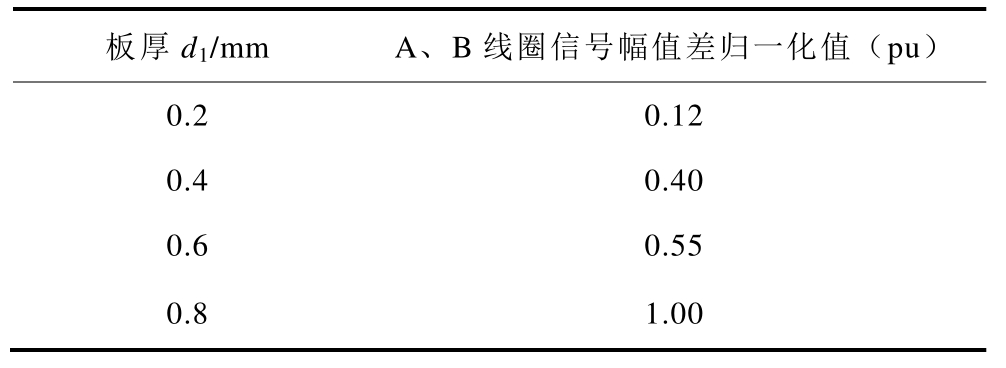
实验结果表明,随着双层电路板厚度的减小,两个线圈的反射回波幅值差减小,当板厚 d1<0.4mm 时,板厚引起的幅值差变化很小。因此,采用厚度0.4mm 以下的电路板制作正交EMAT 线圈对正交横波的影响较小。为尽量减小线圈厚度的影响,本文其他实验中均采用FPC 双面板(厚度0.2mm)制作的正交线圈进行实验。
3.2.4 裂纹深度对A、B 线圈信号幅值的影响
表5 为不同裂纹深度下A、B 线圈接收信号的归一化幅值,实验中裂纹宽度为 0.5mm、长度为150mm 保持不变,数据以完好铝板的接收信号幅值为参考。
表5 A、B 线圈信号幅值与裂纹深度(宽0.5mm,长150mm)
Tab.5 Signal amplitude of A and B coils vs.depth(0.5mm width and 150mm length)
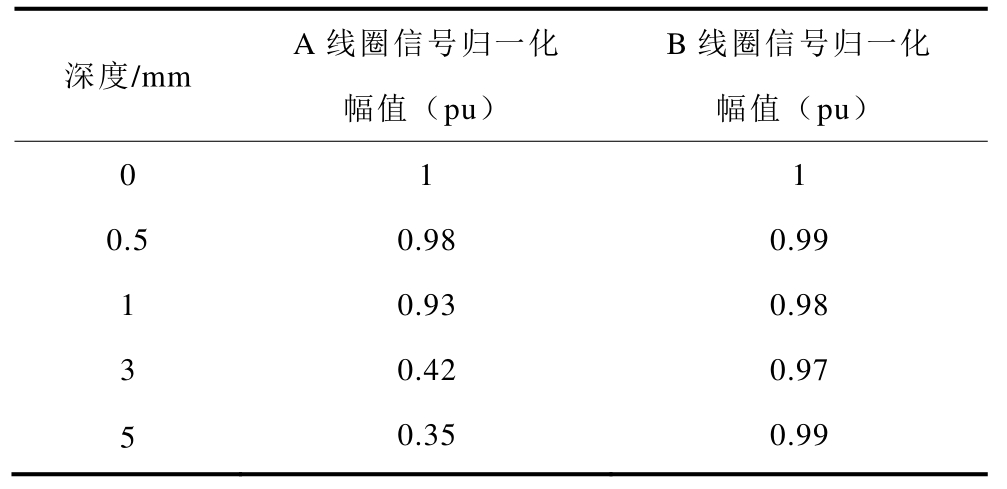
实验结果表明,裂纹深度为0.5~5mm 时,A 线圈接收信号随着裂纹深度增大而明显减小,B 线圈信号幅度则基本不变。原因是裂纹深度越大,与正交横波的相互作用越明显。
从上述分析可以推知,可以利用正交EMAT 检测深度为0.5mm(0.16λ,波长λ=3.12mm)以上、宽度0.5mm 的裂纹。结合仿真结果,当检测深度大于4mm 的裂纹时,接收信号的幅值下降将达到平稳状态。
综上所述,正交线圈EMAT 产生两个相互正交偏振的横波。两个横波在有缺陷的铝板中传播时,幅值存在很大差异。偏振方向与裂纹面垂直的横波在裂纹处产生较大的散射造成明显的幅值下降,而与裂纹面平行的横波则几乎不受影响。利用这一特征,可以同时检测厚度和裂纹,并确定裂纹方向。具体做法为:①换能器同时产生正交偏振横波,通过回波信号的ToF 进行厚度测量,同时比较两个横波反射回波信号的幅值。②如果幅值相差较大,则说明试件内存在裂纹缺陷。根据幅值差与θ 的关系曲线可确定裂纹的方向。在实际检测中,幅值差与θ 的关系曲线可以通过标准试件或对比试件来绘制。③如果两个反射回波幅值相等,则可能存在两种情况:试件底面没有裂纹,或者裂纹角度接近45˚。可将换能器旋转一定角度,如果幅值仍然相等,则可判定为无裂纹;如果出现明显的幅值差,可判定存在45˚的底面裂纹缺陷。
需要指出的是,在实验中如果采用单一线圈的横波EMAT 也可进行厚度检测,但检测裂纹时则需要旋转换能器进行两次脉冲回波实验,并且保持相互垂直的偏振方向,增加实验复杂性,效率低下,难以实现在线检测。因此,与单一线圈的横波EMAT相比,正交偏振的EMAT 可以实现厚度和裂纹的同时检出,且可以定位缺陷方向。此外,与横波与导波复合换能器相比,该换能器结合了横波穿透能力强的优点,对试件厚度没有要求,适合各种厚度管壁裂纹的检测。
4 结论
本文设计了一种正交偏振横波EMAT,通过两个蝶形线圈在铝板中激发正交偏振的横波。对EMAT 激发的声场及其与裂纹缺陷的相互作用进行了三维有限元仿真,得出了利用正交横波可以同时检测铝板厚度、裂纹和裂纹方向。本文的主要结论如下:
1)正交偏振横波EMAT 产生的两个偏振方向的横波在与底面裂纹相互作用时存在很大差异。与裂纹面垂直的横波产生较大的散射造成明显的幅值下降,而与裂纹面平行的横波则几乎不受影响。裂纹深度和长度对垂直裂纹面的横波幅值影响较大,裂纹宽度则影响较小。
2)缩小线圈间距可以减小线圈接收的回波幅度差,提高正交横波声场的对称性,提高检测精度。
3)正交偏振横波EMAT 通过两个线圈接收信号的声时信息和幅值差,可以同时进行厚度测量和对底面垂直裂纹的检测,且可以定位裂纹方向。这为管道内腐蚀减薄和裂纹等缺陷的在线检测提供了新方法。
[1]吴志平,陈振华,戴联双,等.油气管道腐蚀检测技术发展现状与思考[J].油气储运,2020,39(8):851-860.
Wu Zhiping,Chen Zhenhua,Dai Lianshuang,et al.Development status and thinking of oil and gas pipeline corrosion detection technology[J].Oil &Gas Storage and Transportation,2020,39(8):851-860.
[2]帅健,许葵.腐蚀管线失效概率的评定方法[J].石油学报,2003,24(4):86-89.
Shuai Jian,Xu Kui.Assessment method for failure probability of corroded pipeline[J].Acta Petrolei Sinica,2003,24(4):86-89.
[3]杨理践,诸海博,邢燕好,等.基于电磁超声横波的铝板厚度检测技术[J].无损探伤,2016,40(4):10-14.
Yang Lijian,Zhu Haibo,Xing Yanhao,et al.Thickness detection of aluminum plate based on electromagnetic ultrasonic transverse wave[J].Nondestructive Testing Technology,2016,40(4):10-14.
[4]翟国富,梁宝,贾文斌,等.横波电磁超声相控阵换能器设计[J].电工技术学报,2019,34(7):1441-1448.
Zhai Guofu,Liang Bao,Jia Wenbin,et al.Design of the shear wave electromagnetic ultrasonic phased array transducer[J]. Transactions of China Electrotechnical Society,2019,34(7):1441-1448.
[5]王淑娟,李智超,李鹏展,等.非铁磁材料表面波电磁超声换能器接收性能分析与优化设计[J].中国电机工程学报,2015,35(9):2360-2365.
Wang Shujuan,Li Zhichao,Li Pengzhan,et al.Receiving performance analysis and optimal design of surface wave electromagnetic acoustic transducers in nonferromagnetic materials[J].Proceedings of the CSEE,2015,35(9):2360-2365.
[6]孙文秀,刘国强,夏慧,等.非铁磁材料的电磁超声接收过程数值模拟及实验研究[J].电工技术学报,2018,33(19):4443-4449.
Sun Wenxiu,Liu Guoqiang,Xia hui,et al.Numerical simulation and experimental electromagnetic ultrasonic receiving process of non-ferromagnetic materials[J].Transactions of China Electrotechnical Society,2018,33(19):4443-4449.
[7]刘素贞,王淑娟,张闯,等.钢板电磁超声表面波的仿真分析及缺陷定量检测[J].电工技术学报,2020,35(1):97-105.
Liu Suzhen,Wang Shujuan,Zhang Chuang,et al.Electromagnetic acoustic transducer mechanism of steel plate and nonlinear ultrasonic testing of plastic damage[J].Transactions of China Electrotechnical Society,2020,35(1):97-105.
[8]张闯,李雪霏,刘素贞,等.单向载荷下铝板电磁超声兰姆波的波速响应特性[J].电工技术学报,2021,36(8):1579-1586.
Zhang Chuang,Li Xuefei,Liu Suzhen,et al.Wave velocity response characteristics of electromagnetic ultrasonic Lamb wave of aluminum plate under unidirectional load[J].Transactions of China Electrotechnical Society,2021,36(8):1579-1586.
[9]翟国富,李永虔,刘玥怡,等.基于空间域谐波控制的电磁超声Lamb 波模态抑制方法[J].电工技术学报,2021,36(16):3467-3473.
Zhai Guofu,Li Yongqian,Liu Yueyi,et al.Mode suppression method of Lamb wave excited by electromagnetic acoustic transducers based on spatial harmonic control[J]. Transactions of China Electrotechnical Society,2021,36(16):3467-3473.
[10]Hirao M,Ogi H.Electromagnetic acoustic transducers:noncontacting ultrasonic measurements using EMATs[M].Japan:Springer,2017.
[11]Isla J,Cegla F.Optimization of the bias magnetic field of shear wave EMATs[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency,Control,2016,63(8):1148-1160.
[12]江念,王召巴,陈友兴,等.电磁超声检测钢板厚度实验的参数优化[J].传感技术学报,2015,28(4):498-502.
Jiang Nian,Wang Zhaoba,Chen Youxing,et al.The experiment parameters of the steel-sheet thickness measurement by electromagnetic ultrasonic[J].Chinese Journal of Sensors and Actuators,2015,28(4):498-502.
[13]杨能军,封礼发,唐旭明,等.电磁超声横波换能器中线圈的优化设计[J].应用声学,2019,38(3):428-433.
Yang Nengjun,Feng Lifa,Tang Xuming,et al.Optimum design of coil in electromagnetic acoustic shear wave transducers[J].Journal of Applied Acoustics,2019,38(3):428-433.
[14]唐琴,石文泽,卢超,等.多层螺旋线圈电磁超声换能器优化设计及其实验研究[J].中南大学学报(自然科学版),2020,51(7):1792-1803.
Tang Qin,Shi Wenze,Lu Chao,et al.Optimization design and experimental study of multi-layer spiral coils electromagnetic acoustic transducer[J].Journal of Central South University(Science and Technology),2020,51(7):1792-1803.
[15]孙峥,李永虔,杨金旭,等.管道内检测电磁超声在线测厚装置[J].中国测试,2017,43(2):69-72.
Sun Zheng,Li Yongqian,Yang Jinxu,et al.Thickness gauging equipment for ILI of pipelines using EMATs[J].China Measurement &Test,2017,43(2):69-72.
[16]Gan T,Ho K,Billson D,et al.Application of pulse compression signal processing techniques to electromagnetic acoustic transducer for noncontact thickness measurements and imaging[J].American Institute of Physics,2005,76 (5):1-8.
[17]张晓冰,房琦,苏日亮,等.用于检测厚铝板缺陷的体波EMAT 优化方法[J].电机与控制学报,2017,21(1):108-114.
Zhang Xiaobing,Fang Qi,Su Riliang,et al.Optimal method of bulk wave EMATs used in thick aluminum plate with single flat-bottom hole[J].Electric Machines and Control,2017,21(1):108-114.
[18]Howard R.Quantitative evaluation of ultrasonic techniques for the detection and monitoring of corrosion in pipes[D].London:Imperial College London,2017.
[19]苏日亮,康磊,冯剑钊,等.基于电磁超声斜入射SV 波的厚壁管道裂纹检测系统[J].无损检测,2010,32(8):641-644.
Su Riliang,Kang Lei,Feng Jianzhao,et al.Crackinspection device based on electromagnetic acoustic angled shear vertical wave for thick-wall pipelines[J].Nondestructive Testing,2010,32(8):641-644.
[20]赵亮,张金,董子华,等.斜入射SH 波厚壁管道内壁裂纹检测方法[J].应用声学,2020,39(5):747-752.
Zhao Liang,Zhang Jin,Dong Zihua,et al.The detection method of cracks on the inner wall of thick wall pipes with inclined beams of SH waves[J].Journal of Applied Acoustics,2020,39(5):747-752.
[21]ASTM E2192—13 Standard guide for planar flaw height sizing by ultrasonics[S].2013.
[22]叶至灵,韩赞东.燃气管道腐蚀缺陷电磁超声检测方法[J].仪表技术与传感器,2020 (8):100-103.
Ye Zhiling,Han Zandong.Electromagnetic acoustic transducer on corrosion detection of gas pipeline[J].Instrument Technique and Sensor,2020 (8):100-103.
[23]Willems H,Jaskolla B,Sickinger T,et al.A new ILI tool for metal loss inspection of gas pipelines using a combination of ultrasound,eddy current and MFL[C]// ASME International Pipeline Conference,IPC2010,Calgary Alberta Canada,2010:1-8.
[24]唐志峰,孙兴涛,张鹏飞,等.集测厚与导波检测于一体的复合式电磁超声换能器研究[J].仪器仪表学报,2020,41(9):98-109.
Tang Zhifeng,Sun Xingtao,Zhang Pengfei,et al.Research on composite electromagnetic ultrasonic transducer integrating thickness measurement and guided wave detection[J].Chinese Journal of Scientific Instrument,2020,41(9):98-109.
[25]GB/T 33888—2017 无损检测仪器-超声测厚仪特性与验证[S].2017.