0 引言
随着环境和能源问题的日益突出，采用太阳能、风能等新能源分布式发电取得了很大的发展[1]。但其中的电力电子装置等非线性设备会向电网注入谐波[2]，导致电网中的谐波污染日益严重，给电力系统的安全稳定运行造成了不可忽视的影响。对于电网中电压电流等电参数的准确量测是谐波分析治理的关键所在。快速傅里叶变换（Fast Fourier Transform, FFT）因易于嵌入实现的特点，是目前谐波测量分析的最常用算法[3-5]。
国际标准IEC61850-9-2LE中规定，数字化电能计量系统的电参数采样率为256fr或80fr（fr为工频50Hz）[6]。在国际标准IEC61000-4-7中规定在工频50Hz的电网信号采集分析中，进行一次快速傅里叶变换运算的时间窗必须是10个信号周期。这就产生了两个方面的影响：一方面，实际的电力系统频率总是围绕在fr附近波动，同时采样率固定，电压电流的同步采样则得不到保障，在非同步采样下就会产生频谱泄露；另一方面，按照标准规定，采样数据序列长度必定不是2的整数次幂，在进行谐波分析时，无法采用传统的基2快速傅里叶分析算法。
目前非整周期截断和非同步采样引起的频谱泄露问题多采用加窗插值FFT算法解决，国内外学者先后运用余弦窗[7]、三角窗[8]、卷积窗[9]、乘法窗[10]等窗函数对信号序列进行截断，抑制长范围泄露。在插值方面，学者们相继提出双谱线插值[11-12]、三谱线插值[13-14]、四谱线插值[15-16]、六谱线插值[17-18]等算法修正分析结果，抑制短范围泄露。窗函数越来越复杂，插值谱线数目越来越多，虽然提升了谐波分析计算的准确度，但计算的复杂度也随之提升，并且都没有解决FFT对数据序列长度有所限制的问题。如应用较多的基2FFT算法，要求数据序列长度必须是2的整数次幂，加窗插值算法无法解决这个问题。当采样数据序列不是2的整次幂时，可以采用离散傅里叶变换（Discrete Fourier Transform, DFT）运算分析，但是DFT的运算量过于庞大，不利于工程应用。已有文献研究中通常采用补零的方法使数据序列长度满足基2的要求，目前多数补零研究的文献大多直接采用FFT进行计算，较少分析相应的影响。文献[19]分析指出，补零前后的离散傅里叶变换结果不同，补零需要满足一定的规则。文献[20]分析了补零对三谱线插值算法修正公式的影响，以加汉宁窗为例分析研究得出补零后归一化频率、幅值和相位的修正公式。文献[21-24]等探讨研究了混合基FFT在电能质量分析和谐波分析中的应用，得出混合基FFT在非2整次幂数据序列分析中具有一定的应用价值。
针对谐波分析计算中采样数据长度为非2整次幂的情况，本文重点分析了混合基FFT的频谱分布情况，提出一种适用于非整数次幂的高精度混合基FFT谐波测量算法，阐述了其原理和校正过程。该算法的优越性在于对采样数据序列长度没有2整次幂的要求，同时改善了非同步采样下混合基FFT的频谱泄露问题。最后结合仿真及试验分析，验证了其可行性和有效性。
1 常规混合基FFT算法
当对采样数据序列进行FFT分析计算时，序列数据的长度需要满足一定的要求，如基2FFT算法要求数据长度必须是2的整数次幂，基3FFT算法要求数据长度必须是3的整数次幂等。当数据长度不满足要求时，只能采用DFT算法、补零或混合基FFT算法对采样数据序列进行分析。若对采样数据序列直接进行DFT运算，则会导致运算量过于庞大。对于补零运算，在最坏的情况下，需要补加N/2-1个零，也浪费了大量计算资源[25-26]。
对于非2的整数次幂数据序列，只要序列数据长度N是复合数，就可以应用混合基FFT算法[21,27]对其进行分析。N点序列长度x(n)的DFT为
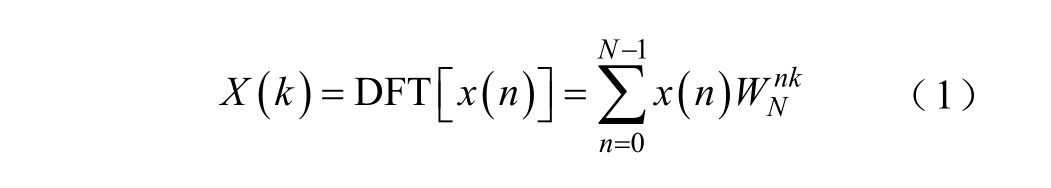
式中，WN为旋转因子，
。当序列数据长度N是2的整数次幂时，可以直接采用基2 FFT算法进行计算；当N不等于2的整数次幂时，N可以表示为两个因子的乘积，即N=N1N2，此时
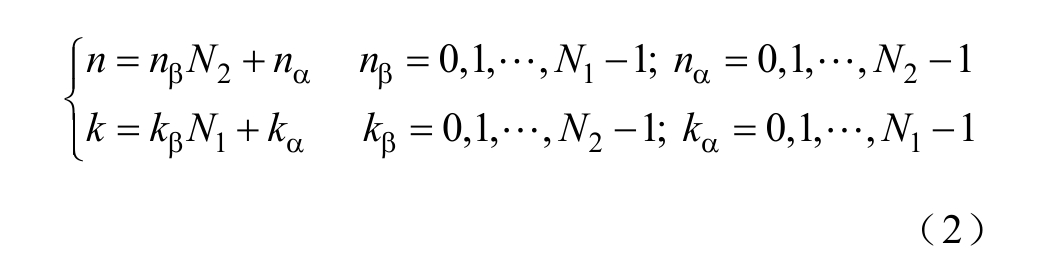
式中，n为N2进制数，nβ为其进位，nα为其末位；k为N1进制数，kβ为其进位，kα为其末位。将n和k代入式（1）得
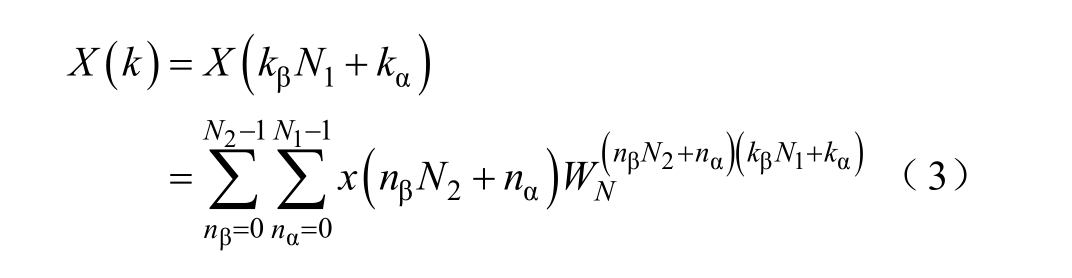
利用旋转因子的特性，可将式（3）化简为
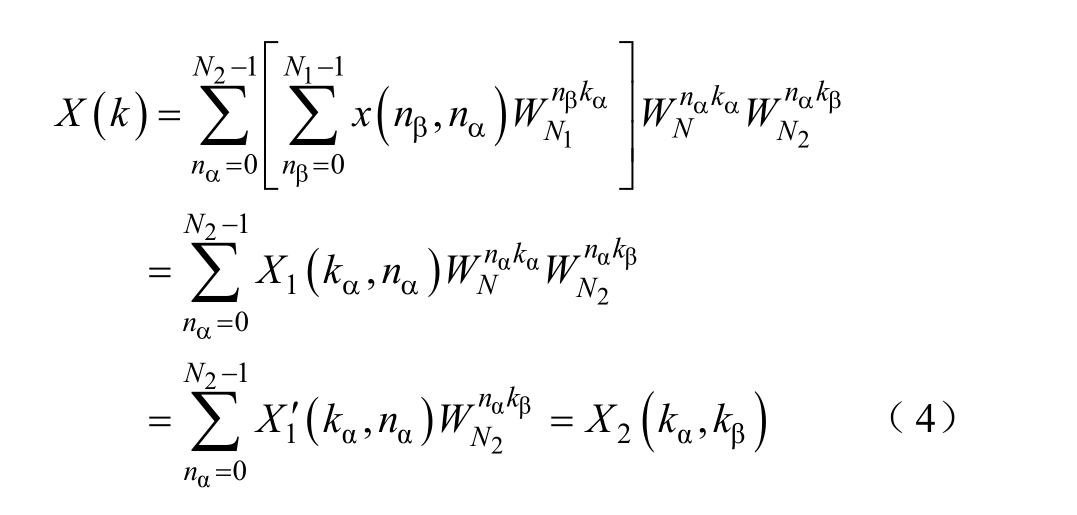
式中，X1(kα,nα)为以nβ为输入、kα为输出的N1点 DFT，
； X2(kα,nβ)为以 nα为输入，kβ为输出的N2点DFT，
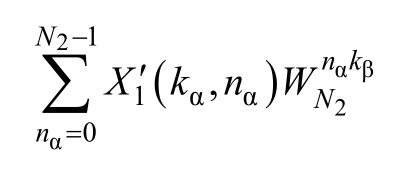。从式（4）可以看出，在计算N点DFT时，可以将N拆分为N1与N2两个因子的乘积，先计算N1点DFT，再计算N2点DFT即可得到结果。若N2仍可表示为多个因子的乘积，可继续向下层分解。当N1或N2存在2的整数次幂时，就可以调用基2FFT算法进行快速计算。
2 高精度混合基FFT谐波测量算法
2.1 混合基FFT频谱谱线分析
一般的谐波信号在时域中的表达式为
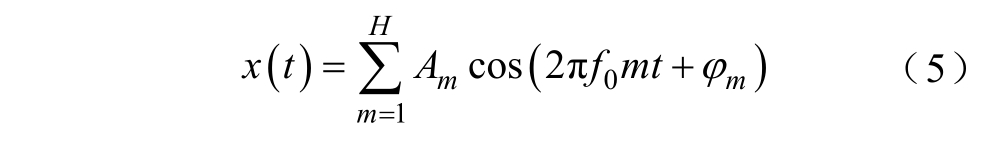
式中，m为谐波次数；H为谐波总次数；f0为基波频率；Am、φm分别为第m次谐波的幅值和初相位。
按照国际标准规定，选取采样10个周波共2 560点数据对式（5）所示信号进行混合基FFT运算。根据常规混合基FFT算法，首先将2 560点数据划分为5组，每组512点数据，需要完成5组512点的基2FFT运算，然后对其结果进行512组5点DFT运算。常规混合基FFT运算的频谱谱线分布如图1所示。
由图1可知，当基波频率偏离50Hz发生变化时，常规混合基FFT算法产生了较大的频谱泄露，使得谐波分析的准确度降低。为说明常规混合基FFT算法目标频点谱线群的分布情况，对图1所示的谱线群加窗，混合基FFT运算加窗后的第m次谐波频谱为
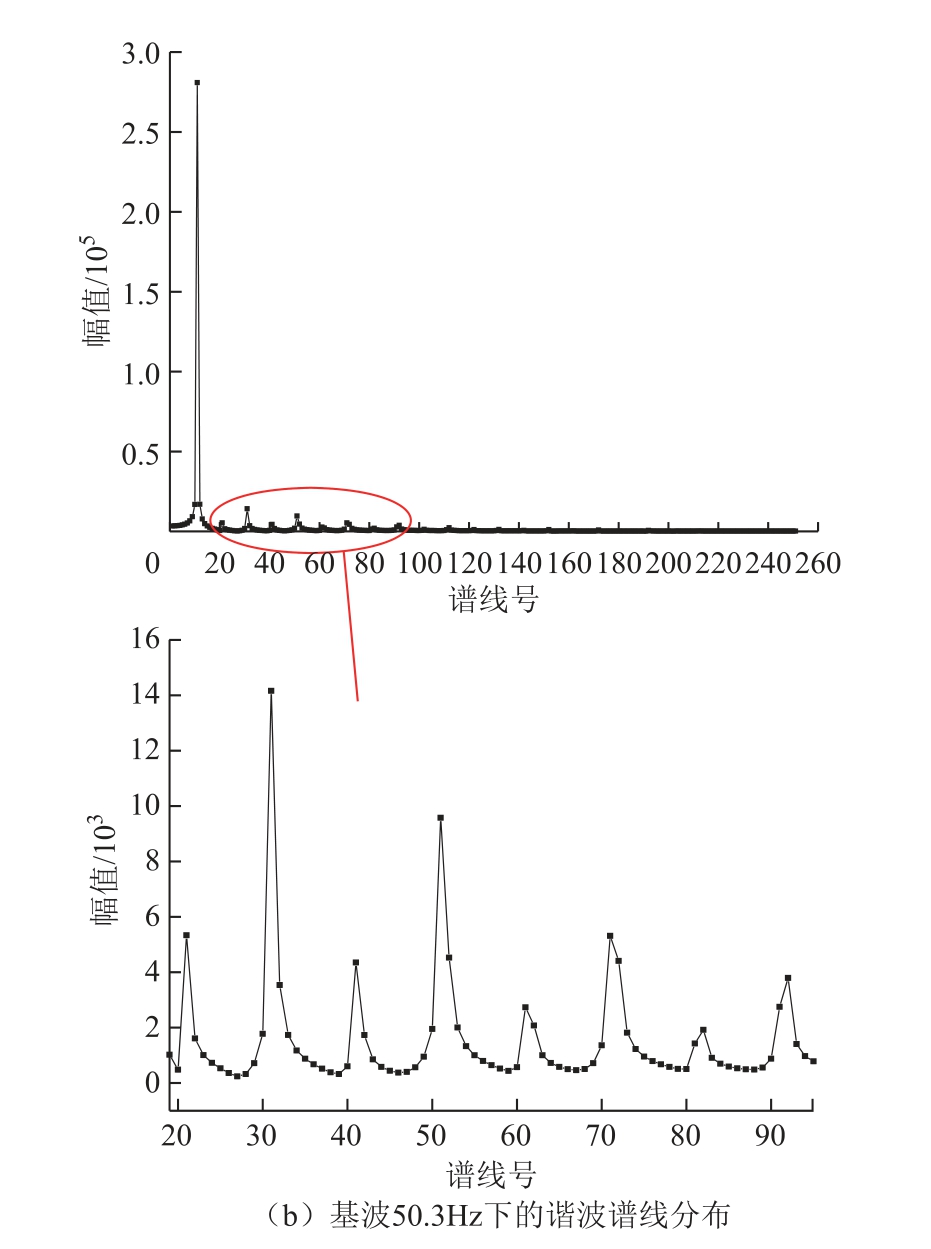
图1 常规混合基FFT运算后的谐波频谱谱线分布
Fig.1 Harmonic spectrum line distribution after conventional mixed-base FFT operation
式中，Δf为频谱分辨率，
；fs为采样速率；km为目标频点即第m次谐波的谱线号； W(ω)为余弦窗的频谱函数。在加窗后的频谱中，目标频点处一般没有离散谱线，依据目标频点谱线、幅值最大谱线和幅值次最大谱线的分布情况，有两种典型的谱线群分布情况，如图2所示。如果采用常规混合基FFT算法对非2整次幂采样数据序列进行分析，则只是用目标频点附近幅值最大谱线的信息估算目标频点的信息，忽略了目标频点附近谱线群中包含的丰富谐波信息，势必会产生较大的分析误差。
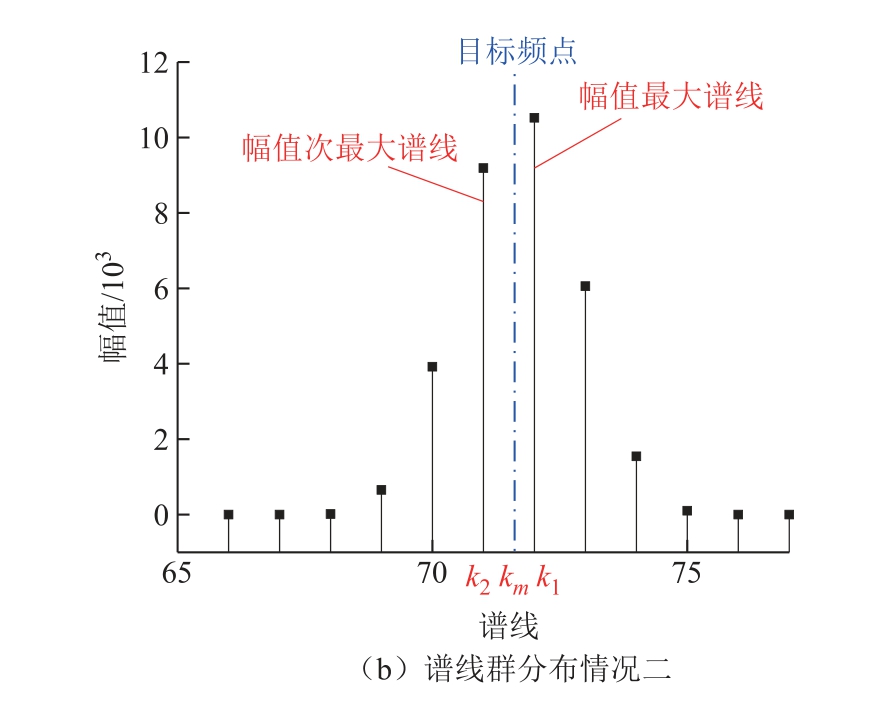
图2 谐波频谱谱线群分布情况
Fig.2 Distribution of harmonic spectral line groups
2.2 高精度混合基FFT测量算法
在图2中，km是目标频点的谱线号，k1、k2、k3、k4依次为目标频点附近幅值按从大到小排列的四根谱线的谱线号。由图2可以明显看出，在对非2整次幂数据序列进行混合基加窗FFT运算后的频谱中，目标频点附近的4根谱线幅值都比较高，含有丰富的谐波信息。设这四条谱线按幅值从大到小的频率为k1Δf、k2Δf、k3Δf、k4Δf，对应的幅值为y1、y2、y3、y4。在图2a所示的情形下，目标频点处幅值最大谱线在目标频点的左侧，有k3＜k1＜km＜k2＜k4，并且 0＜km-k1＜1。令 α= k m - k1 - 0.5，则α∈(-0.5,+0.5)，引入变量
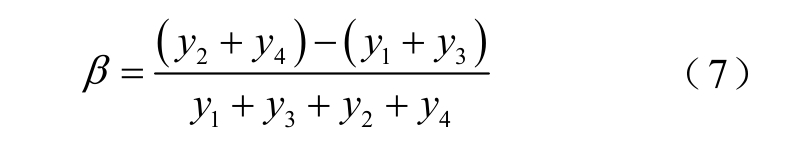
在窗函数的频谱函数 W(ω)中，令ω= 
得
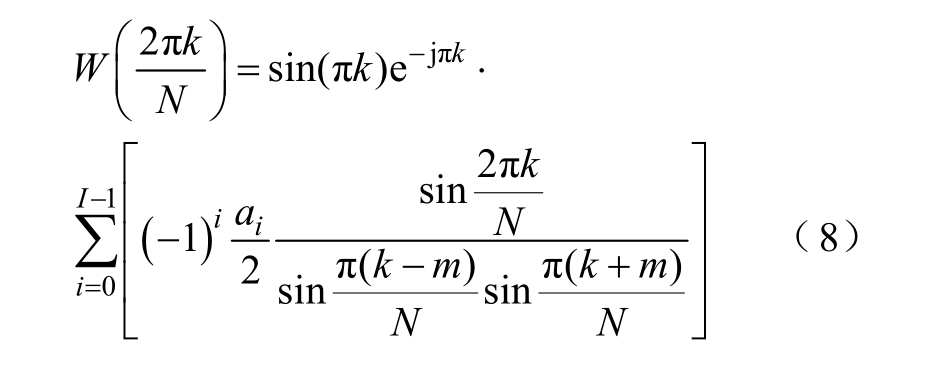
假设
则由式（7）可得
利用多项式曲线拟合得到 α = g(β)，从而得出
按照式（6）修正幅值为
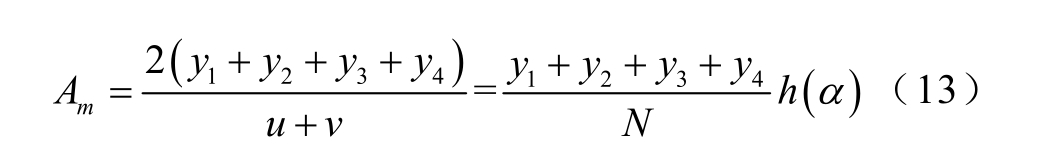
其中，幅值修正式为。
由式（5）和式（6）可得到相位修正式为
式中，arg为求复数辐角函数。
同理，在图2b所示的情况下，目标频点处幅值最大谱线在目标频点的右侧，有k4＜k2＜km＜k1＜k3，并且显然有0＜k1-km＜1，同理令 α= ( k1-k m- 0.5)∈ (-0.5,+0.5)。类似以上可推导得出频率、幅值和相位的修正式分别为
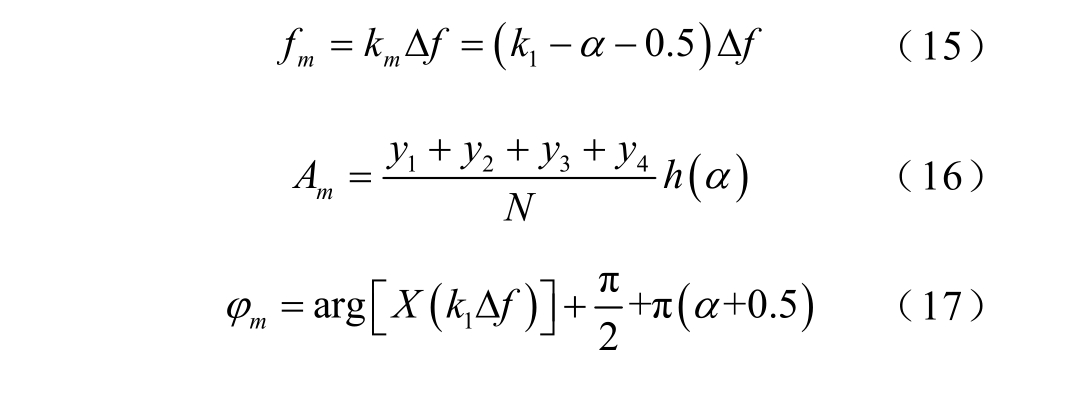
利用多项式曲线拟合函数polyfit()，导出本文采用的四项五阶Nuttall窗的频率、幅值修正式为
3 仿真试验分析
本文所提算法的原理如图3所示，为验证本文提出算法的有效性，选取典型的21次谐波信号进行仿真试验分析，仿真信号模型为
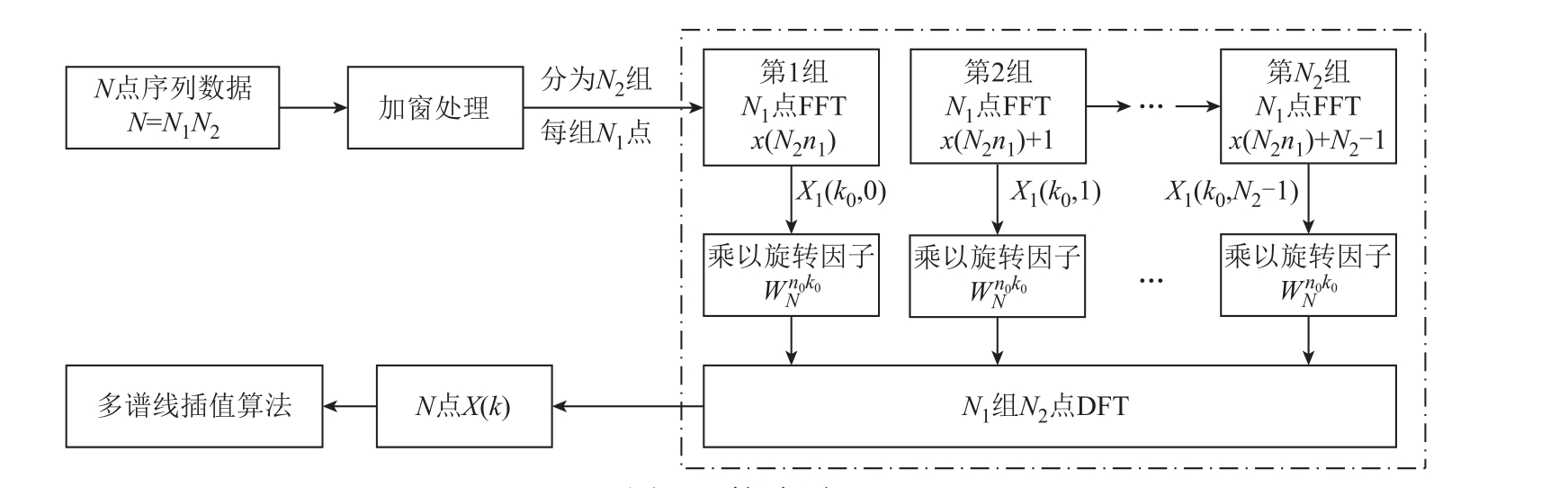
图3 算法原理
Fig.3 The principle diagram of the proposed algorithm
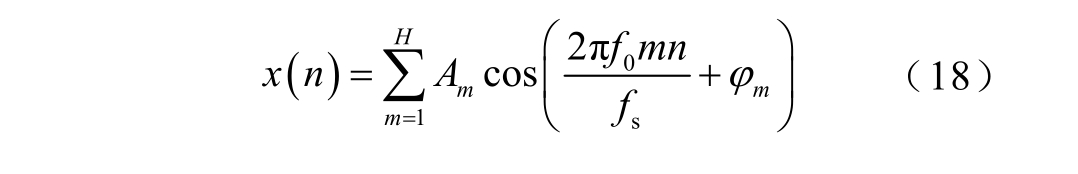
信号参数见表1。依据国际标准IEC61850-9-2LE的规定，本文采用每周波256点的采样速率，依据国际标准IEC61000-4-7规约的规定，本文采样10个周波进行分析。整体算法仿真试验的流程如图4所示。
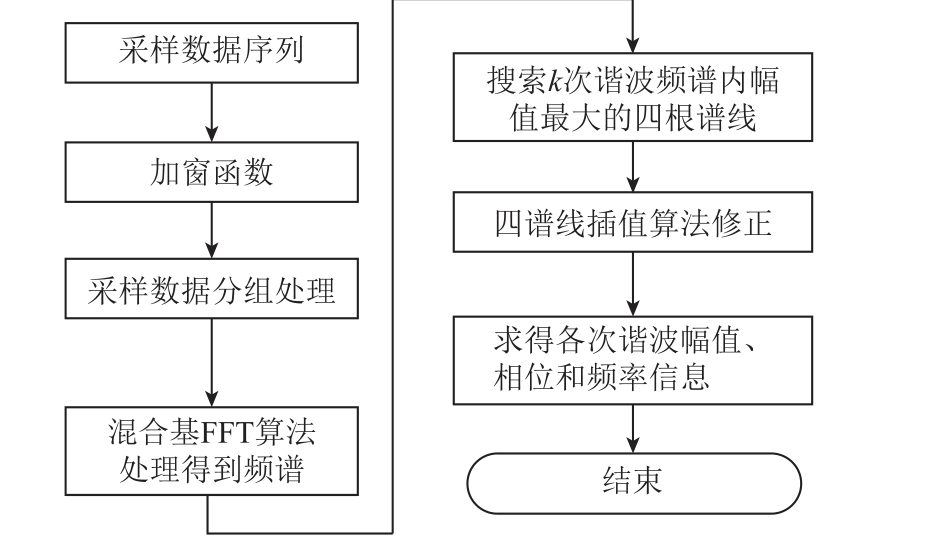
图4 仿真试验流程
Fig.4 Flow chart for simulation experiment
表1 信号参数
Tab.1 Signal parameters
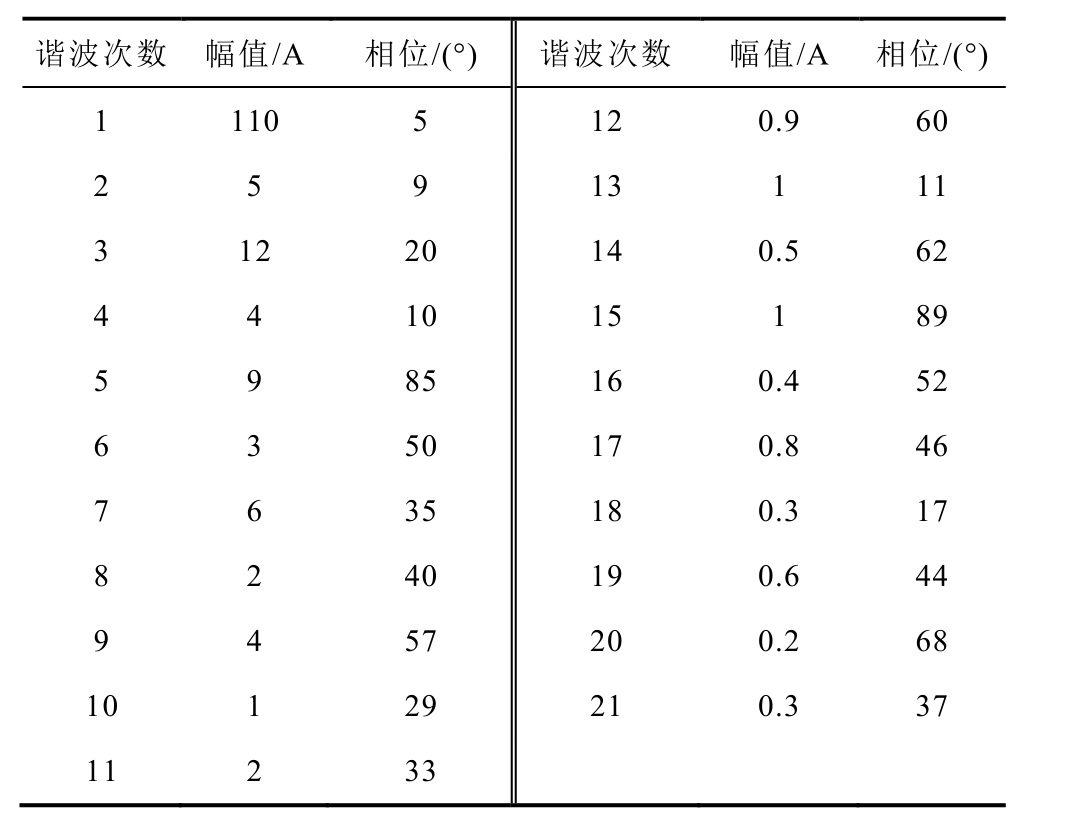
谐波次数 幅值/A 相位/(°) 谐波次数 幅值/A 相位/(°)1 110 5 12 0.9 60 2 5 9 13 1 11 3 12 20 14 0.5 62 4 4 10 15 1 89 5 9 85 16 0.4 52 6 3 50 17 0.8 46 7 6 35 18 0.3 17 8 2 40 19 0.6 44 9 4 57 20 0.2 68 10 1 29 21 0.3 37 11 2 33
3.1 测量准确度分析
取基波频率f0=50.3Hz，依次采用本文所提算法、补零至4 096点采用基2FFT算法（以下简称补零FFT算法）、常规混合基FFT算法对谐波信号进行分析，得到幅值、频率和相位的测量分析结果如图5所示。其中补零FFT算法采用4 096点四谱线插值公式，测量结果都以相对误差的形式给出。图中，m为谐波次数，E(A)为幅值相对误差，E(f)为频率相对误差，E(φ)为相位相对误差。
图5 仿真试验结果 Fig.5 Emulation results
从图5的仿真结果可知，常规混合基FFT算法与补零FFT算法的误差较大，不满足谐波分析的精度要求。说明补零操作对插值算法产生了影响，补零后不能直接采用补零前的插值算法，同时也说明了常规混合基FFT算法在实际谐波测试环境下的实用性不大。本文算法的准确度较高，仿真结果显示，本文算法在21次谐波幅值测量的相对误差不超过7.28×10-4%，相位测量的相对误差不超过1.13×10-3%，频率测量的相对误差不超过1.05×10-5%。故本文提出的混合基FFT多谱线插值算法能有效克服复杂环境的影响，满足高准确度谐波测量的要求。
3.2 基频波动影响分析
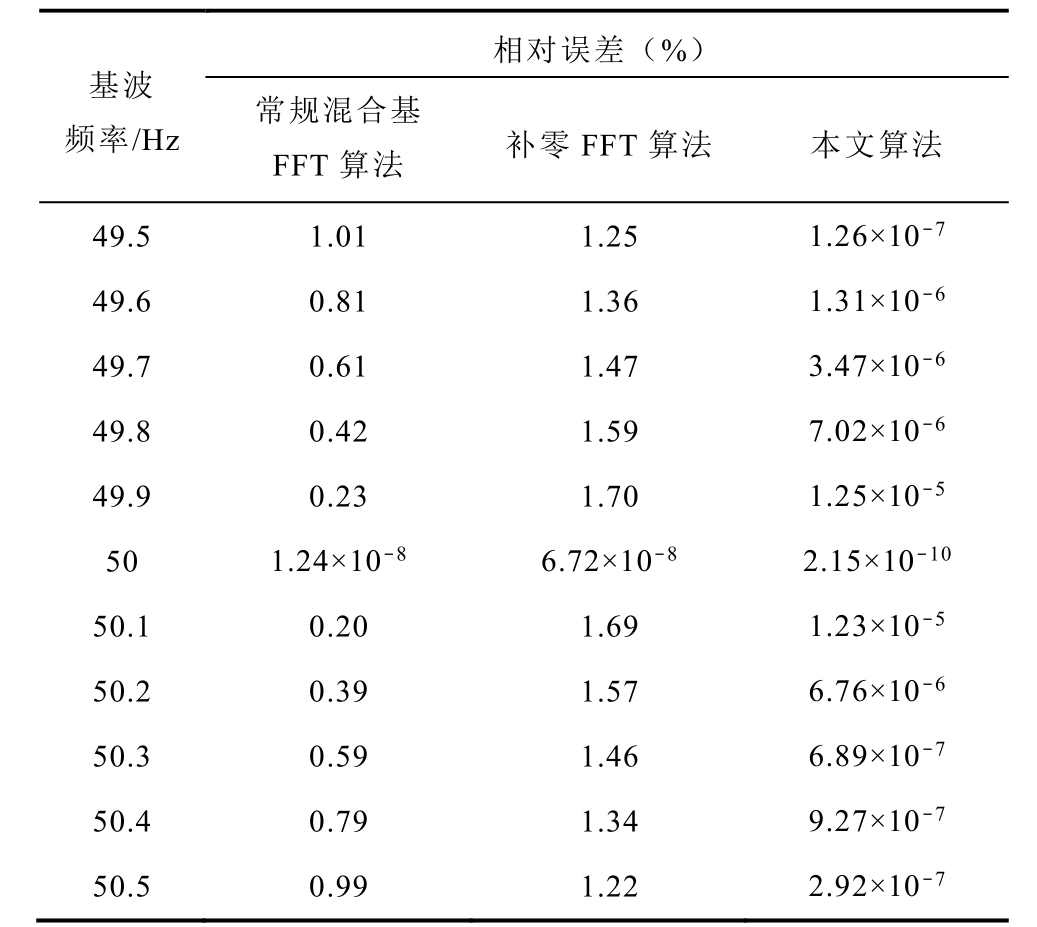
在实际电网环境中，基波频率难以避免地存在波动。为验证本文提出的算法在基频波动影响下的准确度，调整基波频率在49.5～50.5Hz区间内逐渐变化，分别采用本文算法、补零FFT算法、常规混合基FFT算法进行仿真试验分析，得到基波频率波动影响下基波频率的测量相对误差见表2。
表2 基波频率波动下的基波频率相对误差分布
Tab.2 Relative errors of fundamental frequency with frequency changing of fundamental
?
由表2可见，在基波频率波动影响下，常规混合基FFT算法和补零FFT算法已经失准，本文算法的测量相对误差整体稳定在10-5%以下。
在不同基波频率下，采用本文算法对各次谐波幅值进行测量分析，得到各次谐波幅值的相对误差如图6所示。
由表2和图6可以看出，在基波频率波动影响下，采用本文算法对谐波信号测量分析时，基波频率相对误差不超过1.25×10-5%，21次谐波幅值相对误差保持在10-3%以下，与基波频率稳定时相比，谐波幅值的测量精度有所下降，但依然远高于相关标准的测量分析要求。
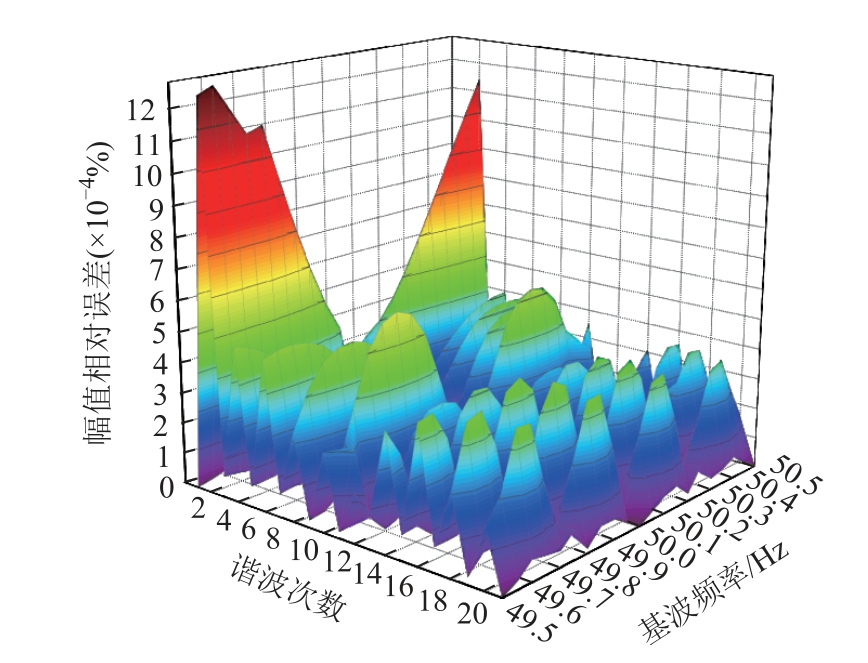
图6 基波波动下的谐波幅值计算相对误差
Fig.6 Relative errors of harmonic amplitude with frequency changing of fundamental
3.3 白噪声影响分析
在实际测量环境下，不可避免地会受到外界干扰噪声的影响。令白噪声的信噪比为60dB，分别采用各算法进行测试分析，得到基波、2次谐波和3次谐波的幅值、频率和相位测量结果见表3。
表3 白噪声影响下的谐波测量分析结果
Tab.3 Analysis results of harmonic measurement under the influence of white noise
?
由表3可见，在噪声影响下本文算法对谐波幅值、频率和相位的测量精度有所降低，但依然高于其余算法，并且满足相关标准的测量分析要求。
为进一步验证本文算法在白噪声影响下的测量准确度，对谐波信号在不同信噪比的白噪声下进行了仿真分析，仍采用式（18）的谐波信号模型，信噪比SNR范围30～100dB，信噪比递进步长为10dB，白噪声影响下谐波幅值的测试分析结果如图7所示。
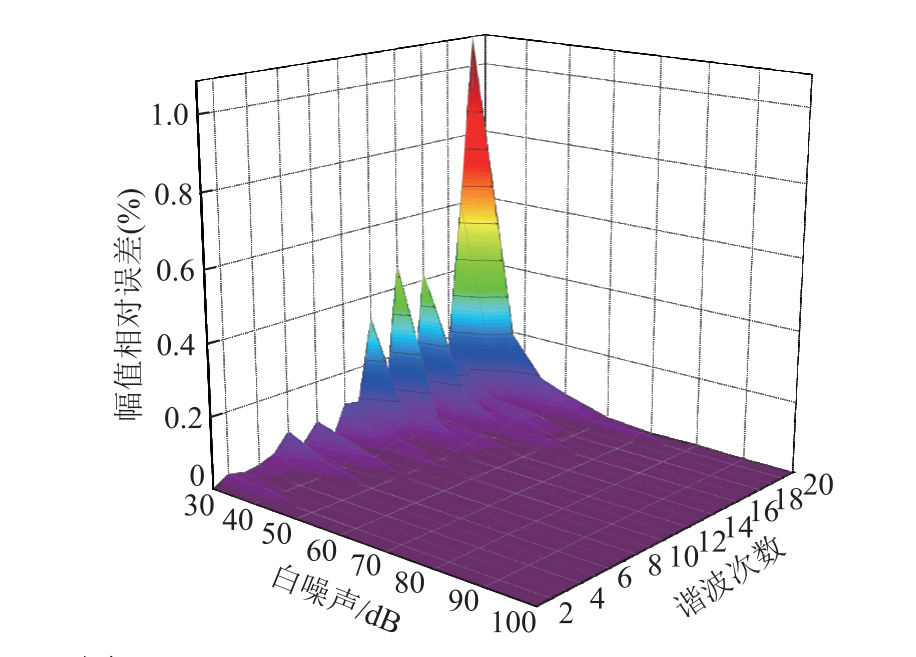
图7 白噪声影响下的谐波幅值相对误差分布
Fig.7 Relative error distribution of amplitude under white noise
由图7可知，当信噪比较低（SNR＜50dB）时，算法的误差明显增加，特别是高次谐波（如19次、20次谐波等）的幅值相对误差较大。当信噪比较高时，21次谐波幅值相对误差不超过0.02%，各次谐波参数的分析精度几乎不受影响，远高于相关标准的要求，故本文算法能有效降低白噪声对谐波检测分析的影响。
3.4 运算量分析
由式（1）可见，进行N点DFT需要N2次复乘运算和N(N-1)次复加运算，进行基2 FFT则需要
次复乘运算和 2logN N次复加运算。按照国际标准规定，对于采样10个周波共2 560点数据的情况，采用本文算法的复乘和复加运算量分别为
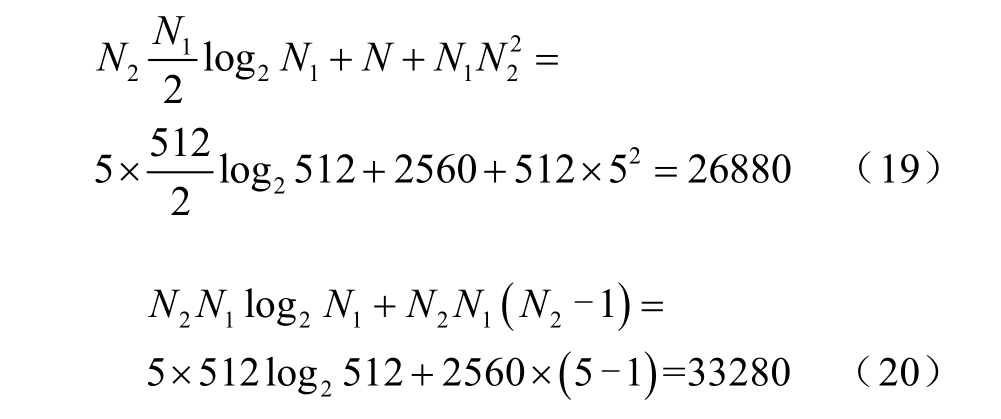
算法运算量的对比见表4。从表4中可以看出，与DFT算法相比，本文算法的运算量大大减少，与补零至基2FFT算法的运算量相差不多，但精度却大大增加。故对于非2整次幂的数据序列分析而言，本文算法具有一定的应用价值。
表4 算法运算量对比
Tab.4 Comparison of algorithm computation
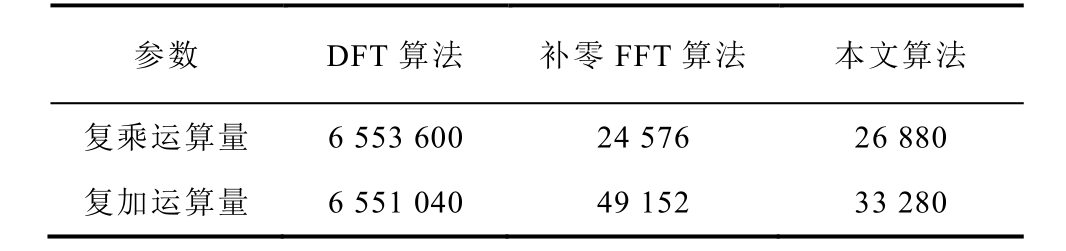
参数 DFT算法 补零FFT算法 本文算法 复乘运算量 6 553 600 24 576 26 880 复加运算量 6 551 040 49 152 33 280
4 试验分析
采用德州仪器公司的MSP430F6459作为主控MCU搭建了试验平台，其结构如图8所示。其中，高精密程控源发出的谐波信号经过预处理电路后，被模数转换器AD7606采样得到数字信号采样序列。主控MCU采用本文算法对信号采样序列分析处理，得到的分析结果将在上位机上显示。
图8 试验平台框图
Fig.8 Diagram of the test platform
试验中谐波信号的基波频率为50.3Hz，在IAR Embedded Workbench编译软件中编写算法后，在此试验平台上对多种算法进行了试验验证，上位机得到的试验结果见表5。
表5 试验结果
Tab.5 Experiment results
幅值相对误差（%） 分析对象常规混合基FFT算法 补零FFT算法 本文算法 基波 0.045 19.356 4.63×10-4 2次谐波0.181 19.742 3.55×10-3 3次谐波0.418 20.062 2.54×10-3 4次谐波0.725 20.325 4.82×10-3 5次谐波1.138 20.827 3.42×10-3
由表5可以看出，在非2整数次幂数据序列的谐波分析中，常规混合基FFT算法与补零FFT算法的误差较大，不能满足谐波分析的精度要求。在此试验平台上，本文算法对基波和谐波幅值的分析准确度达到10-3%、10-4%的数量级。若在0.2级的数字化智能电表中进行谐波电能计量，本文算法误差的影响将会很小。
此外，本文算法在试验分析中的准确度与仿真分析结果相比有所降低，并非完全一致，其差异主要由信号源自身的误差、模数转换器的量化误差以及电路板上的电磁干扰所引起的。如模数转换器AD7606的基准温度系数为±10×10-6℃，若试验过程中AD7606芯片的温度变化范围为±5℃，则引入的误差为±0.005%，再加上AD7606的积分非线性和微分非线性误差，模数转换器引入的误差约为±0.006 5%。此外，信号预处理电路中的仪表运算放大器在固定增益下也存在精度误差和温漂，这些误差的引入最终都会导致上位机接收到的数据精度有所降低。因此对试验平台的进一步完善改进也是后续的研究工作之一。
5 结论
针对谐波分析中采样数据序列是非2整数次幂的情形，在分析常规混合基FFT算法的不足，并充分考虑目标频点附近谱线信息的基础上，提出一种适用于非整数次幂的高精度混合基FFT的谐波测量算法。该算法以2 560点采样序列为例，将其分解为5点DFT运算和基2FFT运算，依据混合基FFT频谱分布情况采用四条谱线插值校正计算，并且根据不同情况分别推导出了不同的修正公式。仿真及试验结果表明，对于非2整数次幂数据序列，相比于其余分析算法，本文算法具有更高的谐波分析准确度，并能有效地改善基波偏移和白噪声产生的影响，具有很高的应用研究前景。
[1]王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[2]邵振国, 黄伟达. 考虑出力不确定性的分布式电源谐波传播计算[J]. 电工技术学报, 2019, 34(2): 674-683.
Shao Zhenguo, Huang Weida. A calculation method of harmonic propagation considering the uncertainty of distributed generation[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 674-683.
[3]温和, 滕召胜, 王永, 等. 改进加窗插值FFT 动态谐波分析算法及应用[J]. 电工技术学报, 2012, 27(12): 270-277.
Wen He, Teng Zhaosheng, Wang Yong, et al. Improved windowed interpolation FFT algorithm and application for power harmonic analysis[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 270-277.
[4]李振华, 胡廷和, 杜亚伟, 等. 基于窗函数和谱线插值理论的谐波检测方法[J]. 电力系统保护与控制, 2019, 47(22): 78-88.
Li Zhenhua, Hu Tinghe, Du Yawei, et al. Harmonic detection method based on the theory of windows and spectrum line interpolation[J]. Power System Protection and Control, 2019, 47(22): 78-88.
[5]肖勇, 赵伟, 黄松岭. 基于离散傅里叶级数的非同步采样下谐波功率测量算法[J]. 电工技术学报, 2018, 33(7): 1570-1578.
Xiao Yong, Zhao Wei, Huang Songling. Harmonic power measurement algorithm based on discrete fourier series in asynchronous sampling[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1570-1578.
[6]肖勇, 罗睿希, 赵伟, 等. 基于IEC61850的数字化电能表用快速准同步谐波测量算法[J]. 电网技术, 2018, 42(2): 621-627.
Xiao Yong, Luo Ruixi, Zhao Wei, et al. Fast quasisynchronous harmonic algorithm for IEC61850 based digital energy metering devices[J]. Power System Technology, 2018, 42(2): 621-627.
[7]张荣伦, 王帅, 穆海宝, 等. 大型电力变压器损耗带电测试技术研究[J]. 电工技术学报, 2019, 34(4): 683-692.
Zhang Ronglun, Wang Shuai, Mu Haibao, et al. The on site method for the loss characteristic in power transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 683-692.
[8]潘文, 钱俞寿, 周鹗. 基于加窗插值FFT的电力谐波测量理论(Ⅰ)窗函数研究[J]. 电工技术学报,1994, 9(1): 50-54.
Pan Wen, Qian Yushou, Zhou E. Power harmonics measurement based on windows and interpolated FFT(Ⅰ)study of windows[J]. Transactions of China Electrotechnical Society, 1994, 9(1): 50-54.
[9]张介秋, 梁昌宏, 陈砚圃. 一类新的窗函数——卷积窗及其应用[J]. 中国科学E 辑, 2005, 35(7): 773-784.
Zhang Jieqiu, Liang Changhong, Chen Yanpu. A new family of windows—convolution windows and their applications[J]. Science in China, Series E: Technological Sciences, 2005, 35(7): 773-784.
[10]张俊敏, 刘开培, 汪立, 等. 基于乘法窗函数的插值FFT的谐波分析方法[J]. 电力系统保护与控制, 2016, 44(13): 1-5.
Zhang Junmin, Liu Kaipei, Wang Li, et al. An algorithm for harmonic analysis based on multiplication window function[J]. Power System Protection and Control, 2016, 44(13): 1-5.
[11]潘文, 钱俞寿, 周鹗. 基于加窗插值FFT的电力谐波测量理论(Ⅱ)双插值FFT理论[J].电工技术学报,1994, 9(2): 53-56.
Pan Wen, Qian Yushou, Zhou E. Power harmonics measurement based on windows and interpolated FFT(Ⅱ) dual interpolated FFT algorithms[J]. Transactions of China Electrotechnical Society, 1994, 9(2): 53-56.
[12]卿柏元, 滕召胜, 高云鹏, 等. 基于Nuttall窗双谱线插值FFT的电力谐波分析方法[J]. 中国电机工程学报, 2008, 28(25): 153-158.
Qing Baiyuan, Teng Zhaosheng, Gao Yunpeng, et al. An approach for electrical harmonic analysis based on nuttall window double-spectrum-line interpolation FFT[J]. Proceedings of the CSEE, 2008, 28(25): 153-158.
[13]牛胜锁, 梁志瑞, 张建华, 等. 基于三谱线插值FFT的电力谐波分析算法[J]. 中国电机工程学报, 2012, 32(16): 130-136.
Niu Shengsuo, Liang Zhirui, Zhang Jianhua, et al. An algorithm for electrical harmonic analysis based on triple-spectrum-1ine interpolation FFT[J]. Proceedings of the CSEE, 2012, 32(16): 130-136.
[14]黄冬梅, 龚仁喜, 焦凤昌, 等. 莱夫-文森特窗三谱线插值的电力谐波分析[J]. 电力系统保护与控制, 2014, 42(2): 28-34.
Huang Dongmei, Gong Renxi, Jiao Fengchang, et al. Power harmonic analysis based on Rife-Vincent window and triple-spectral-line interpolation[J]. Power System Protection and Control, 2014, 42(2): 28-34.
[15]李得民, 何怡刚. 基于Nuttall窗四谱线插值FFT的电力谐波分析[J]. 电力系统保护与控制, 2016, 44(3): 64-71.
Li Demin, He Yigang. Harmonic analysis of power system based on Nuttall window four-spectrum-line interpolation FFT[J]. Power System Protection and Control, 2016, 44(3): 64-71.
[16]郝柱, 顾伟, 褚建新, 等. 基于四谱线插值FFT的电网谐波检测方法[J]. 电力系统保护与控制, 2014, 42(19): 107-113.
Hao Zhu, Gu Wei, Chu Jianxin, et al. A power network harmonic detection method based on the fourspectrum-line interpolation FFT[J]. Power System Protection and Control, 2014, 42(19): 107-113.
[17]王保帅, 肖霞. 一种用于谐波分析的高精度多谱线插值算法[J]. 电工技术学报, 2018, 33(3): 553-562.
Wang Baoshuai, Xiao Xia. A high accuracy multispectrum-line interpolation algorithm for harmonic analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 553-562.
[18]华敏, 陈剑云. 一种高精度六谱线插值FFT谐波与间谐波分析方法[J]. 电力系统保护与控制, 2019, 47(11): 9-15.
Hua Min, Chen Jianyun. A high precision approach for harmonic and interharmonic analysis based on sixspectrum-line interpolation FFT[J]. Power System Protection and Control, 2019, 47(11): 9-15.
[19]王冰, 申卫昌, 田来科, 等. 快速傅立叶变换Cooley-Tukey算法补零问题[J]. 西北大学学报（自然科学版）, 2004, 34(1): 31-33.
Wang Bing, Shen Weichang, Tian Laike, et al. A study on the problem of add zero in the algorithm of Cooley-Tukey fast Fourier transfrom[J]. Journal of Northwest University (Natural Science Edition), 2004, 34(1): 31-33.
[20]翟晓军, 周波. 一种改进的插值FFT谐波分析算法[J]. 中国电机工程学报, 2016, 36(11): 2952-2958.
Zhai Xiaojun, Zhou Bo. An improved interpolated FFT algorithm for harmonic analysis[J]. Proceedings of the CSEE, 2016, 36(11): 2952-2958.
[21]Xiao Yong, Zhao Wei, Chen Lei, et al. Fast quasisynchronous harmonic algorithm based on weight window function-mixed radix FFT[C]//IEEE International Workshop on Applied Measurements for Power Systems, Germany, Aachen, 2016: 1-6.
[22]Yin Xin, Zhang Aimin, Zhang Hang, et al. Research and design of digital power quality analysis system based on mixed radix FFT[C]//Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 2014: 7393-7399.
[23]Toshiji K. Harmonic analysis of power electronic systems using the mixed radix FFT[C]// Proceedings of 14 Annual Conference of Industrial Electronics Society, Singapore, 1988: 581-586.
[24]Lu I D, Lee P. Use of mixed radix FFT in electric power system studies[J]. IEEE Transactions on Power Delivery, 1994, 9(3): 1276-1280.
[25]胡广书. 数字信号处理理论、算法与实现[M]. 3版.北京: 清华大学出版社，2012.
[26]高培生. 电力系统中的间谐波频谱分析[D]. 杭州: 浙江大学, 2008.
[27]李刚. 电能质量分析仪中同步采样方法及电参数检测研究与实现[D]. 成都: 电子科技大学, 2016.